高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

顾及空间邻接关系的多级河流线状矢量数据并行压缩算法

,  ,  ,  ,  , 

上一篇

下一篇

朱晓波, 周廷刚, 曾波, 等. 顾及空间邻接关系的多级河流线状矢量数据并行压缩算法[J]. 西南大学学报（自然科学版）, 2017, 39(2): 100-106. doi: 10.13718/j.cnki.xdzk.2017.02.016
引用本文: 朱晓波, 周廷刚, 曾波, 等. 顾及空间邻接关系的多级河流线状矢量数据并行压缩算法[J]. 西南大学学报（自然科学版）, 2017, 39(2): 100-106. doi: 10.13718/j.cnki.xdzk.2017.02.016
shu
Xiao-bo ZHU, Ting-gang ZHOU, Bo ZENG, et al. Evaluation of Resources and Environment Carrying Capacity Based on Topsis of Grey Correlation Method and GIS in Chongqing City[J]. Journal of Southwest University Natural Science Edition, 2017, 39(2): 100-106. doi: 10.13718/j.cnki.xdzk.2017.02.016
Citation: Xiao-bo ZHU, Ting-gang ZHOU, Bo ZENG, et al. Evaluation of Resources and Environment Carrying Capacity Based on Topsis of Grey Correlation Method and GIS in Chongqing City[J]. Journal of Southwest University Natural Science Edition, 2017, 39(2): 100-106. doi: 10.13718/j.cnki.xdzk.2017.02.016
shu

顾及空间邻接关系的多级河流线状矢量数据并行压缩算法

  • 1.

    三峡库区生态环境教育部重点实验室, 重庆 400715

  • 2.

    西南大学 地理科学学院, 重庆 400715

  • 3.

    西南大学 生命科学学院, 重庆 400715

  • 基金项目: 三峡后续工作库区生态与生物多样性保护专项项目(5000002013BB5200002)；国家自然科学基金项目(41301417)；重庆市基础与前沿计划(cstc2014jcyjA20017)
详细信息
    作者简介:

    朱晓波(1990-), 男, 山西永济人, 博士研究生, 主要从事环境遥感与地理信息系统应用研究 .

    通讯作者: 周廷刚, 教授, 硕士研究生导师; 

  • 中图分类号: P208

Evaluation of Resources and Environment Carrying Capacity Based on Topsis of Grey Correlation Method and GIS in Chongqing City

  • 1.

    Key Laboratory of Eco-Environments in Three Gorges Reservoir Region (Ministry of Education), Chongqing 400715, China

  • 2.

    School of Geographical Sciences, Southwest University, Chongqing 400715, China

  • 3.

    School of Life Sciences, Southwest University, Chongqing 400715, China

  • 摘要: 提出了一种顾及空间邻接关系的多级河流线状矢量数据并行压缩算法.首先利用拓扑分析和网络分析提取多级河流矢量数据的空间邻接结点, 并对Douglas-Peucker算法进行改进；然后基于数据并行的任务分配方式, 设计多级河流矢量数据并行压缩算法, 并利用消息传递接口和C语言对该算法进行编程实现；最后设计验证性实验, 利用该算法对三峡库区重庆段的多级河流矢量数据进行压缩.研究表明:利用该算法压缩多级河流矢量数据的空间邻接结点保持率达到100%, 同时相对于串行算法, 计算节点为4时平均加速比可达2.507, 提高了压缩效率.
    Abstract: This paper proposes a parallel compression algorithm for multilevel river vector data considering spatial adjacency relations. The algorithm is composed of several steps. Firstly, in order to keep the spatial adjacency relations of multilevel rivers, the spatial adjacency nodes of multilevel river vector data are extracted by topology analysis and network analysis. Then the Douglas-Peucker algorithm is improved to keep these spatial adjacency nodes in the process of compression. In this way, a serial compression algorithm for multilevel river vector data is proposed. Next, on the basis of establishing the task allocation method and communication method, this paper proposes a parallel compression algorithm for multilevel river vector data, and the algorithm is implemented using message passing interface (MPI) and C programming language. Finally, the parallel compression algorithm is applied to compress the vector data of multilevel rivers in the Three Gorges Reservoir Area of Chongqing. The results show that the spatial adjacency nodes retention rate of multilevel river vector data can reach an average of 100% using the proposed parallel compression algorithm. Meanwhile, the speed-up ratio can reach an average of 2.507 with 4 compute nodes using the parallel compression algorithm comparing with serial compression algorithm, the compression efficiency of multilevel river vector data is improved.
  • 加载中

  • 图 1  Douglas-Peucker算法压缩多级河流数据时的空间邻接关系不一致现象

    下载: 全尺寸图片 幻灯片

    图 2  多级河流矢量数据串行压缩算法流程图

    下载: 全尺寸图片 幻灯片

    图 3  多级河流矢量数据并行压缩算法流程图

    下载: 全尺寸图片 幻灯片

    图 4  阈值为1 000 m时不同算法压缩效果对比

    下载: 全尺寸图片 幻灯片

    表 1  压缩有效性比较

    阈值/
    m    		Douglas-Peucker算法多级河流矢量数据并行压缩算法
    相对位移
    偏差    		空间邻接结点
    保持率/%    		压缩率/
    %    		相对位移
    偏差    		空间邻接结点
    保持率/%    		压缩率/
    %
    1000.000 3574.2129.680.000 29100.0029.54
    2000.001 2271.8345.020.001 01100.0044.76
    3000.002 1071.2754.470.001 76100.0054.3
    4000.002 9965.6360.840.002 43100.0060.59
    5000.003 8765.2965.140.003 17100.0064.95
    6000.005 9762.2868.280.005 04100.0068.18
    7000.008 1561.6770.700.006 82100.0070.63
    8000.010 3559.8872.800.008 64100.0072.61
    9000.012 6459.2474.250.010 62100.0074.16
    1 0000.014 8857.1675.710.012 43100.0075.52
    平均值0.006 2564.850.005 22100.00
    下载: 导出CSV

    表 2  并行算法与串行算法运行结果对比

    阈值/
    m    		串行算法运行时间/
    s    		p=2p=4
    并行算法运行时间/s加速比并行算法运行时间/s加速比
    1007.8024.8431.6112.9482.647
    2007.1854.3351.6572.8152.552
    3006.7793.9971.6962.6862.524
    4006.5023.6531.7802.6222.480
    5006.3133.4841.8122.5332.492
    6006.1643.3431.8442.4772.488
    7006.0433.2331.8692.4472.470
    8005.9403.1681.8752.4252.449
    9005.8633.0891.8982.3702.474
    1 0005.7903.0341.9082.3562.458
    平均值6.4383.6181.7792.5682.507
    下载: 导出CSV
  • [1] DOUGLAS D, PEUCKER T. Algorithms for the Deduction of the Number of Points Required to Represent a Digitized Line or Its Caricature [J]. The Canadian Cartographer, 1973, 10(2): 112-122. doi: 10.3138/FM57-6770-U75U-7727
    [2] 于靖, 陈刚, 张笑, 等.面向自然岸线抽稀的改进道格拉斯—普克算法[J].测绘科学, 2015, 40(4): 24-27. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-CHKD201504006.htm
    [3] WU S T, MARQUEZ M R G. A Non-Self-intersection Douglas-Peucker Algorithm [C] // Proceedings of the 16th Brazilian Symposiumon on Computer Graphics and Image Processing. Sao Carlos, Brazil: IEEE Computer Society, 2003: 60-66.
    [4] 杨得志, 王杰臣, 闾国年.矢量数据压缩的Douglas-Peucker算法的实现与改进[J].测绘通报, 2002(7): 18-22. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-JYRJ201001045.htm
    [5] 谢亦才, 林渝淇, 李岩. Douglas-Peucker算法在无拓扑矢量数据压缩中的新改进[J].计算机应用与软件, 2010, 27(1): 141-144. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-JYRJ201001045.htm
    [6] 卢云娥, 黄宗宇, 李超阳, 等.基于微机集群系统的MPI并行计算[J].电子设计工程, 2011, 19(5): 78-81. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-GWDZ201105032.htm
    [7] 江岭, 汤国安, 刘凯, 等.局部地形因子并行计算方法研究[J].地球信息科学学报, 2012, 14(6): 761-767. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-DQXX201206014.htm
    [8] 唐俊奇.多处理机系统中曲面轮廓图像处理的并行化研究[J].西南大学学报(自然科学版), 2014, 36(2): 156-163. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-XNND201402027.htm
    [9] 刘军志, 朱阿兴, 秦承志, 等.分布式水文模型的并行计算研究进展[J].地理科学进展, 2013, 32(4): 538-547. doi: 10.11820/dlkxjz.2013.04.006
    [10] 沈婕, 郭立帅, 朱伟, 等.消息传递接口环境下等高线简化并行计算适宜性研究[J].测绘学报, 2013, 42(4): 621-628. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201304026.htm
    [11] 马劲松, 沈婕, 徐寿成.利用Douglas-Peucker并行算法在多核处理器上实时综合地图线要素[J].武汉大学学报(信息科学版), 2011, 36(12): 1423-1426. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-WHCH201112010.htm
    [12] 吴信才, 刘少雄.基于邻接关系的空间数据挖掘[J].计算机工程, 2002, 28(7): 89-91. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-WJFZ200704041.htm
    [13] 陈国良. 并行算法的设计与分析[M].北京: 高等教育出版社, 2002: 22-23.
    [14] 刘志强, 宋君强, 卢凤顺, 等.非平衡进程到达模式下MPI广播的性能优化方法[J].软件学报, 2011, 22(10): 2509-2522. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-RJXB201110024.htm
    [15] 王净, 江刚武.无拓扑矢量数据快速压缩算法的研究与实现[J].测绘学报, 2003, 32(2): 173-177. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-CHXB200302016.htm
  • 加载中
图( 4) 表( 2)
计量
  • 文章访问数:  1295
  • HTML全文浏览数:  524
  • PDF下载数:  50
  • 施引文献:  0
出版历程
  • 收稿日期:  2016-01-28
  • 刊出日期:  2017-02-20

顾及空间邻接关系的多级河流线状矢量数据并行压缩算法

    通讯作者: 周廷刚, 教授, 硕士研究生导师; 
    作者简介: 朱晓波(1990-), 男, 山西永济人, 博士研究生, 主要从事环境遥感与地理信息系统应用研究
  • 1. 三峡库区生态环境教育部重点实验室, 重庆 400715
  • 2. 西南大学 地理科学学院, 重庆 400715
  • 3. 西南大学 生命科学学院, 重庆 400715
  • 收稿日期:  2016-01-28
基金项目:  三峡后续工作库区生态与生物多样性保护专项项目(5000002013BB5200002)；国家自然科学基金项目(41301417)；重庆市基础与前沿计划(cstc2014jcyjA20017)

摘要: 提出了一种顾及空间邻接关系的多级河流线状矢量数据并行压缩算法.首先利用拓扑分析和网络分析提取多级河流矢量数据的空间邻接结点, 并对Douglas-Peucker算法进行改进；然后基于数据并行的任务分配方式, 设计多级河流矢量数据并行压缩算法, 并利用消息传递接口和C语言对该算法进行编程实现；最后设计验证性实验, 利用该算法对三峡库区重庆段的多级河流矢量数据进行压缩.研究表明:利用该算法压缩多级河流矢量数据的空间邻接结点保持率达到100%, 同时相对于串行算法, 计算节点为4时平均加速比可达2.507, 提高了压缩效率.

English Abstract

    全文HTML

  • 在地理信息系统(GIS)的空间数据模型中, 河流通常以线状矢量数据的形式进行存储.近年来, 随着数字地图的广泛应用和WebGIS的迅猛发展, 大范围、高精度的多级河流矢量数据占用存储空间大、网络传输速度慢的问题越来越突出, 因此, 迫切需要一种能够合理并高效压缩多级河流矢量数据的方法.

    经典的矢量数据压缩算法有光栏法、垂距限值法、角度限值法、Douglas-Peucker算法[1]等.其中, Douglas-Peucker算法从曲线的整体特征出发进行压缩, 具有平移、旋转的不变性的特点, 并且实现简单, 效率较高, 压缩效果好[2], 得到了广泛应用.其基本原理为:对于目标曲线, 首先设定一个距离阈值D, 然后将曲线首尾2点相连形成一条线段, 对于曲线上的其余各点, 求其与此线段的距离, 并记下最大距离Dmax；比较Dmax与D的大小, 若Dmax＜D, 则将曲线上的中间各点全部舍去；若Dmax＞D, 则以该最大距离点为界, 将曲线分为2部分, 再分别对这2部分重复以上过程, 直到结束.

    国内外已有不少学者对Douglas-Peucker算法及其改进算法进行了研究, 如任意阈值下曲线无自相交简化的算法[3]；利用径向距离作为曲线内点取舍的补充约束条件, 对Douglas-Peucker算法进行改进, 有效控制其压缩的面积误差[4]；公共边对象化Douglas-Peucker改进算法[5], 通过将公共边的相关信息封装成类, 解决压缩公共边时出现“裂缝”问题等.上述研究对Douglas-Peucker算法进行了不同程度的改进, 改善了压缩质量, 但针对的均是普通的矢量数据, 而多级河流矢量数据有其自己的特征, 如支流与干流之间的空间邻接关系, 利用常规的矢量数据压缩方法往往会丢失空间特征信息.与此同时, 随着数据量的增加, 传统的串行计算技术和单纯地对压缩算法进行优化已达到瓶颈.为了满足快速、高效压缩矢量数据的要求, 迫切需要新的思路和方法提高压缩效率.

    并行计算是相对于串行计算而言的, 是指在同一时间间隔内增加操作系统进程数、利用多台计算机共同实现一个任务的计算方法[6], 在数字地形分析[7]、图像处理[8]、水文模型[9]等许多领域具有广泛的应用.在矢量数据压缩的并行计算方面, 近年来也有学者进行了一定的研究, 如对不同的等高线压缩算法进行并行计算的适宜性研究[10], 在综合考虑算法时间复杂度等多个因素的基础上分析了压缩算法的并行计算适宜性；利用Douglas-Peucker并行算法在多核处理器上实时综合地图线要素[11], 将串行Douglas-Peucker算法改进为使用多核处理器的并行算法等.本文将矢量数据压缩算法与并行计算技术结合, 在Douglas-Peucker算法的基础上提出了一种顾及空间邻接关系的多级河流矢量数据并行压缩算法, 以期在保持空间邻接关系的前提下, 实现多级河流矢量数据的快速、高效压缩.

1.   多级河流矢量数据串行压缩算法

    1.1.   多级河流空间邻接关系保持方法

  • 空间关系是空间实体之间由于空间位置和形状的不同而形成的相互之间的各种联系[12].邻接关系是其中的一种表现形式, 具体到多级河流数据中则体现为干流与支流之间的邻接关系.由于Douglas-Peucker算法每次针对单个曲线进行压缩, 如果直接利用该算法压缩多级河流数据, 会造成压缩后多级河流之间断裂等空间邻接关系的不一致现象(图 1).因此, 在压缩多级河流数据时, 有必要对Douglas-Peucker算法进行改进, 以保持其空间邻接关系.

    保持多级河流空间邻接关系的关键在于压缩时多级河流之间邻接结点的保存, 为此要提取待压缩数据的空间邻接结点.本文利用ArcGIS对多级河流矢量数据的邻接结点进行提取.具体方法为:首先对多级河流矢量数据建立拓扑关系；其次建立河流网络数据, 通过网络分析模块提取网络数据中各线之间的结合点；最后建立河流数据与结合点之间的空间连接关系, 生成结合点的Join_Count属性(即该点连接的线个数), 删除Join_Count小于3的点, 余下的即为多级河流的空间邻接结点.

    • 1.2.   算法流程

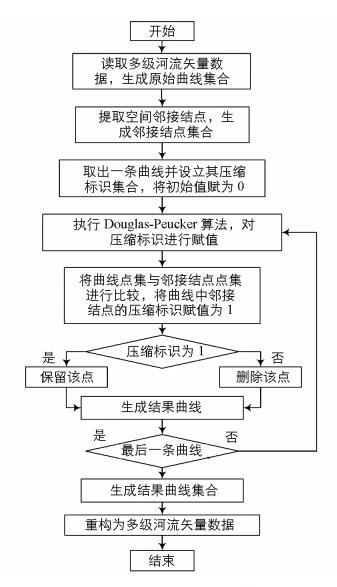
  • 在提取空间邻接结点的基础上, 顾及空间邻接关系的多级河流矢量数据串行压缩算法流程见图 2.

    1) 读取多级河流矢量数据, 生成原始曲线集合Lini{L0, L1, …, Ln-1}, 其中每条曲线由一个点集P{P0, P1, …, Pm-1}构成, 记录曲线中每个点的地理坐标(x, y).

    2) 提取多级河流数据的空间邻接结点, 生成邻接结点点集R{R0, R1, …, Rr-1}.

    3) 对于每条曲线的点集P, 设立压缩标识集合F{F0, F1, …, Fm-1}, F的编号与点集中点的编号一一对应, 其初始值为0.以任意点Pi(0 ≤ i ≤ m-1) 为例, 当Fi=0时, 舍弃Pi点；Fi=1时, 保留Pi点.

    4) 设定压缩阈值, 逐条曲线执行Douglas-Peucker算法, 对曲线中每个点的压缩标识F进行赋值, 然后将点集P与邻接结点的点集R进行比较, 当二者之中有相同的点时(即坐标相等), 将其压缩标识F赋值为1.

    5) 利用压缩标识F逐条曲线执行判断, 当Fi=0时, 将Pi点从点集P中舍去；Fi=1时, 保留Pi点.将压缩后的点集P整合为结果曲线集合Lres{L0, L1, …, Ln-1}, 并重构为多级河流矢量数据, 完成压缩.

2.   多级河流矢量数据并行压缩算法设计

    2.1.   并行计算模式

  • 近年来, 各种并行硬件和软件层出不穷, 本文选择目前较为流行的MPI(Message Passing Interface)作为并行计算的开发环境.主从模式和对等模式是MPI的2种基本并行计算模式[13].主从模式中, 主节点负责管理和协调其他子节点；对等模式中, 各计算节点地位相同.根据多级河流矢量数据压缩算法的特点, 本文采用主从模式, 算法描述如下:由主节点对压缩任务进行划分, 并将任务分配到各子节点；各子节点负责各自的压缩任务, 并将结果返回给主节点；主节点完成压缩结果的合并与输出.

    • 2.2.   任务分配

  • 并行计算的任务分配有任务并行和数据并行2种模式.任务并行是将需要执行的各个任务分配到各计算节点上执行；数据并行是将需要处理的数据分配给各计算节点, 再由各节点对分配到的数据进行相似的操作.本文提出的压缩算法中, 由于压缩过程相对简单且联系较为紧密, 不易进行任务分解；而多级河流矢量数据以曲线集合的形式进行存储, 便于数据分割.因此, 本文采用数据并行的方法进行任务的分配, 即将待压缩的曲线集合分配到各个计算节点上分别进行压缩.

    • 2.3.   通信方式

  • 根据任务分配方式, 各计算节点执行各自的压缩任务后, 需要将结果返回给主节点, 并由主节点完成结果的合并与输出, 这需要通过节点间的通信来实现.

    MPI提供了集合通信和点对点通信2种方式[14].由于集合通信要求每次传输的数据量相同, 而各计算节点分配到的曲线段数据量并不相同.因此, 本文采用点对点的通信方式, 即在各子节点完成压缩任务后, 通过调用MPI_Send函数将各曲线的压缩结果返回给主节点, 主节点通过调用MPI_Recv函数接收数据；完成所有子节点的数据接收工作后, 主节点将各子节点的压缩结果进行合并, 重新形成曲线集合, 完成压缩任务.

    • 2.4.   并行算法流程

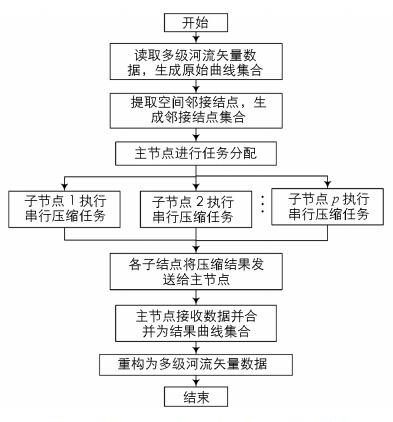
  • 在确定并行计算模式、任务分配和通信方式的基础上, 本文设计了多级河流线状矢量数据的并行压缩算法(图 3), 具体流程如下:① 读取多级河流矢量数据和空间邻接结点数据, 由主节点通过任务分配方式将数据分发给各子计算节点. ② 各子节点执行多级河流矢量数据串行压缩算法, 完成各自的压缩任务. ③ 各子节点通过通信方式将压缩结果返回给主节点, 同时由主节点进行数据接收和合并, 在所有曲线完成压缩后生成结果曲线集合Lres{L0, L1, …, Ln-1}. ④ 由主节点将结果曲线集合重构为多级河流矢量数据, 完成压缩.

3.   结果与分析

    3.1.   实验验证设计与结果

  • 为了评估多级河流矢量数据并行压缩算法的有效性, 本文设计了验证性实验.实验环境为4台微机构成的小型集群系统, 微机的配置为:Inter(R) Core(TM) i5-4460 CPU @ 3.20GHz四核, 8GB内存.编程环境为Visual Studio 2012和MPICH2 1.4.1p1, 使用C语言开发.试验数据采用三峡库区重庆段的河流1:25万矢量数据, shapefile格式, 大小为16.9 MB.空间邻接结点采用ArcGIS 10.2软件平台进行提取.设置不同阈值时分别利用Douglas-Peucker算法和本文提出的多级河流矢量数据并行压缩算法进行压缩.由于原数据河网过于密集, 本文只对长江及部分主要支流进行显示, 压缩算法有效性评估见表 1, 并行算法与串行算法运行结果见表 2.

    线状矢量数据压缩的精度评定一般采用点位评估法[15], 即通过原始曲线上点与压缩后曲线的相对位移偏差大小来衡量压缩精度, 多级河流矢量数据的相对位移偏差计算方法如下:

    式中:ε为相对位移偏差；Li为第i条河流曲线压缩前长度；n为河流曲线总条数；Di为第i条河流曲线压缩后的平均位移偏差, 计算方法如下:

    式中:di表示压缩前河流曲线中第i个坐标点与压缩后河流曲线的距离；m为此条河流曲线压缩前的坐标点个数.

    加速比是衡量串行运算和并行运算时间关系的一个指标, 其计算方法为:

    式中:v为阈值；p为节点数；S(v, p)为加速比；Ts(v), Tp(v, p)分别为串行运算时间和并行运算时间.

    • 3.2.   分析与结论

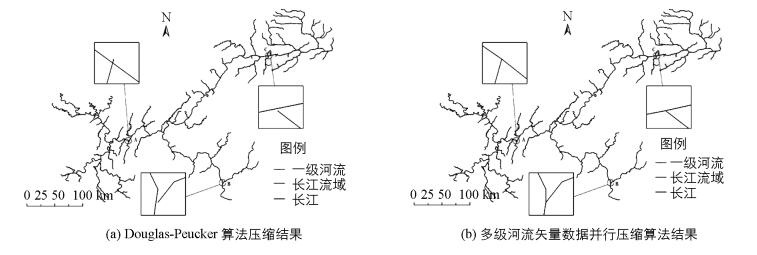
  • 1) 数据压缩有效性分析.利用Douglas-Peucker算法进行压缩时, 压缩后的多级河流矢量数据出现拓扑关系丢失现象(图 4(a)), 而本文提出的多级河流矢量数据并行压缩算法不会出现拓扑关系丢失(图 4(b)).同时, 由表 1可知, 在阈值为100 m、500 m、1 000 m时, Douglas-Peucker算法压缩结果的相对位移偏差分别为0.000 35, 0.003 87, 0.014 88, 空间邻接结点保持率分别为74.21%, 65.29%, 57.16%, 压缩率分别为29.68%, 65.14%, 75.71%；而多级河流矢量数据并行压缩算法压缩结果的相对位移偏差分别为0.000 29, 0.003 17, 0.012 43, 空间邻接结点保持率均为100%, 压缩率分别为29.54%, 64.95%, 75.52%.结果表明, 顾及空间邻接关系的多级河流矢量数据并行压缩算法可完整地保持空间邻接关系, 且由于保留了空间邻接结点, 与Douglas-Peucker算法相比压缩精度有所提高, 但同时压缩率有所降低, 这是因为消耗了存储空间用于储存空间邻接结点.

    2) 串行与并行算法结果比较分析.由表 2可知, 在阈值为100 m、500 m、1 000 m时, 串行算法的运行时间分别为7.802 s, 6.313 s, 5.79 s；计算节点p=2时并行算法的运行时间分别为4.843 s, 3.484 s, 3.034 s, 加速比分别为1.611, 1.812, 1.908；p=4时的运行时间分别为2.948, 2.533, 2.356, 加速比分别为2.647, 2.492, 2.458.说明并行算法比串行算法的运行效率更高, 且计算节点为4时的运行时间要少于计算节点为2时的运行时间. p=2和p=4时平均加速比分别为1.779和2.507, 并不能达到理想的状态(即S=p).这是因为并行计算并不是简单地将计算任务平均分配给各子节点执行, 在实际计算中, 并行算法会在节点间通信上比串行算法花费额外的时间, 而且会受到节点间网络环境的影响, 甚至可能会遇到信息阻塞、程序死锁等问题.

4.   结论

  • 1) 顾及空间邻接关系的多级河流线状矢量数据并行压缩算法能有效保持空间邻接关系.利用该算法进行压缩时, 多级河流矢量数据的平均相对位移偏差为0.005 22, 与Douglas-Peucker算法相比降低了16.48%；空间邻接结点保持率达到100%, 比Douglas-Peucker算法平均提高了35.15%, 在有效地压缩多级河流矢量数据的同时, 保持了其空间邻接关系.

    2) 并行压缩算法能有效提高压缩效率.与串行算法比较, 在不同阈值条件下, 并行算法运行时间明显缩短, 计算节点为4时平均加速比达到2.507, 提高了多级河流矢量数据的压缩效率.

    3) 如何保持压缩时多级河流的其他空间关系, 如保证多级河流在简化后不出现错误交叉的现象, 尚需进行进一步的研究.

参考文献 (15)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回