-
重庆地处中亚热带西部,主城区座落在长江与嘉陵江汇合处,两江环抱,依山建城,公路蜿蜒曲折,上下盘旋,是典型的山城,面积5 468.7 km2.重庆主城区属东亚内陆季风区,夏季受西南夏季风影响,高温、多雨,是我国暴雨频发的大城市之一.在全球变暖的大背景下,虽然不同地区有所差异,但极端强降水的频率和强度整体呈增大趋势,给城市市政排水带来了更大的潜在压力[1].如2007年“7·17”强降水事件,造成重庆市沙坪坝区陈家桥镇城市排水不及,积涝严重,交通、电力、通信、供水、供气一度中断,上万名群众被困,造成了严重的社会影响和经济损失. 2009年8月4日,暴雨袭击重庆,重庆主城主干道不少路段积水严重,山城变泽国;千年古镇磁器口临江房屋已快被江水没顶,当地居民只能乘船来往通行. 2010年7月11日重庆市因城市内涝灾害,交通多处中断,92架航班延误. 2013年,重庆西部暴雨造成潼南、铜梁等区县近90万人受灾,主城区六区多处道路积水严重.靳俊伟等[2]探讨了重庆主城区排水(防涝)综合规划总体技术路线,指出原规划设计排水标准偏低、部分管段施工不规范等累计导致排水系统的抗风险能力不足.为了应对气候变化和经济社会发展需求,做好城市暴雨内涝防御工作,提高城市排水规划及工程设计的科学性,迫切需要重新核定城市排水管渠标准,增强重庆市城市道路排水能力.
邱兆富等[3]、罗雅文[4]、金超[5]、郭渠等[6]对重庆主城区的暴雨强度公式进行了推算,但关于重庆地区暴雨雨型的研究一直没有涉及.雨型包括:降水空间分布雨型和时间变化雨型[7],其中时间变化雨型是描述降雨过程的概念,是降雨强度在时间尺度上的分配过程,含设计暴雨量和设计暴雨过程两部分[8].文献[9]对降水空间分布雨型进行了研究,文献[10-11]对设计暴雨过程作了研究.迄今为此,关于设计暴雨量的研究尚未见报道.由于篇幅所限,本文仅研究重庆市主城区时间变化雨型中的设计暴雨量部分,设计暴雨过程部分将另文分析.设计暴雨量是城市雨水排除系统设计标准的重要组成部分,与社会经济水平有着非常密切的关系,其重现期的大小关系着城市雨水排除系统的规模以及是否能够达到其抵御暴雨灾害的目的,同时也是城市雨污分流管道系统的关键技术参数和设计防洪及水利工程设施的重要指标.
本文试图采用皮尔逊Ⅲ型分布、耿贝尔分布、指数分布、对数正态分布、广义帕雷托(GP)分布拟合推算不同重现期的设计暴雨量,并与现行《室外排水设计规范》(GB50014-2006,2014版)推荐计算方法—暴雨强度公式计算结果进行比较,选择适合重庆主城区设计暴雨量,这将为重庆主城区城市雨水灾害防治管理、预警和应急处置及城市勘查设计等提供理论依据和技术支持.
全文HTML
-
重庆市气候中心根据中国气象局组织编制的“降水自记纸彩色扫描数字化处理系统”,对重庆市沙坪坝(57516) 气象站的降水自记纸资料进行了数字化处理,形成了1961-2013年逐年逐分钟降水序列.在资料使用前对原始数据进行了严格质量检查、审核与一致性分析,数据完整率为100%.
-
暴雨取样方法:水文统计学的取样方法有年最大值法和非年最大值法两类.本研究采用年最大值法与年多个样法两种方法,年多个样法是非年最大值法中的一种,在城市暴雨强度公式编制中应用较为广泛.年最大值法是60,120,180,360,540,720,1 440 min(下称各历时)每年各选一个最大值,年多个样法是每年每个历时挑选前8个最大值,分别建立重庆市主城区沙坪坝1961-2013年年最大值法、年多个样法的暴雨资料样本.
关于降水极值的理论概率分布,目前尚无公认的统一模型,本文选用国内外应用比较广泛的Pearson-Ⅲ分布、Gumbel分布、Exponential分布、Log-normal分布函数,分别拟合1961-2013年年最大值法各历时序列分布;采用GP分布函数对年多个样法资料进行分布拟合,其中Pearson-Ⅲ分布、Gumbel分布、Exponential分布在城市暴雨强度公式的统计中应用较为广泛[1].研究表明,采用上述5种方法对各历时降水极值的概率分布进行研究是可行的[11-14],但是每种分布函数都有其适用性,没有一种分布函数能够适合所有的数据[15],至于哪种更为适合一直处于争论之中.这5种方法的数学表达式见文献[12, 15-18],应用相关系数、相对误差、柯尔莫哥洛夫—斯米尔洛夫检验方法(K-S)为检验指标[19],对各方法分布拟合效果进行检验,选取最优概率模型拟合推算不同重现期的设计暴雨量.
1.1. 数据
1.2. 方法
-
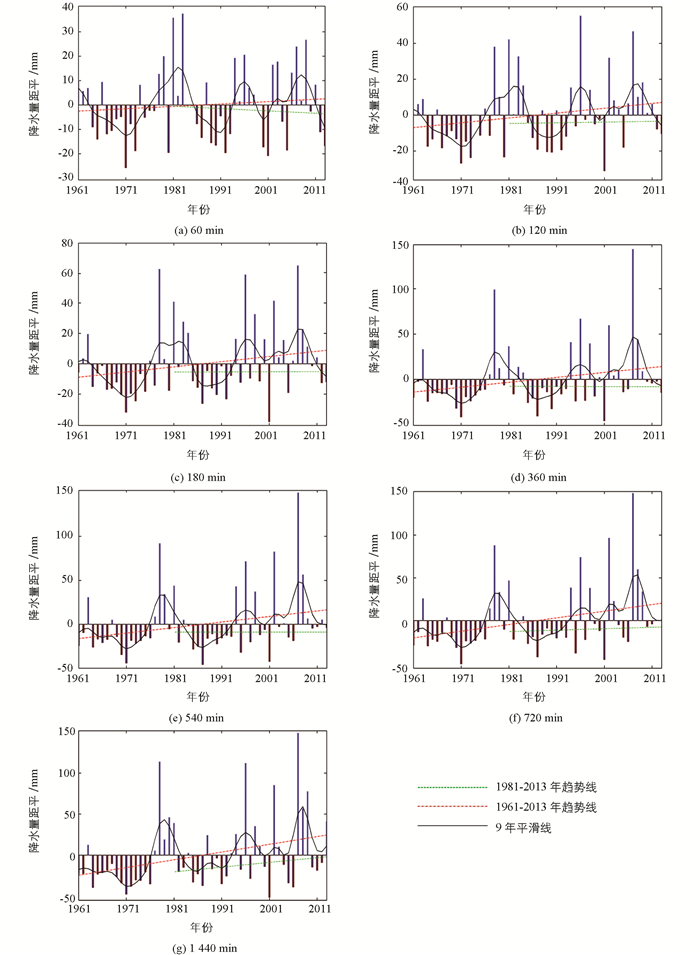
从沙坪坝站1961-2013年60 min年最大降雨量变化趋势(图 1)可以看出,60 min年最大降雨量年际差异较大,大值主要集中在20世纪70年代末至80年代初、90年代中后期和2010年.其中,1983年最大(80 mm),1971年最小(16.9 mm). 1961-2013年,重庆市主城区60 min年最大降雨量平均为42.6 mm,呈小幅增加趋势,增加率为1.0 mm/10a.
同60 min年最大降雨量趋势变化类似,53年来,120,180,360,540,720,1 440 min年最大降雨量呈增多趋势,增加趋势分别为2.7,3.4,5.4,6.4,7.8,9.4 mm/10a,其中360,540,720,1 440 min变化趋势在0.05的检验水平上分析具有统计学意义.各历时年最大降雨量的年际差异明显,在20世纪70年代末至80年代初、90年代中后期至今偏多.如:20世纪70年代中期前、80年代至90年代中期1 440 min年最大降雨量偏少,其余时段偏多,其中2007年7月19时37分钟开始的1 440 min降雨量达271.0 mm,为历年之最.
-
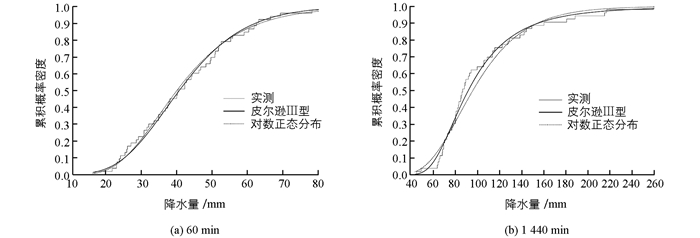
采用年最大值法选样所得样本,该样本不论大雨年或小雨年都有1个资料被选入,其机率为严密的一年一遇发生值,按极值理论,当资料年份很长时,它近似于全部资料选样的计算值,选出的资料独立性强,资料的收集也较容易,在1980年以来的地面气象记录年报表中,均能查到各历时的年最大降雨量. Pearson-Ⅲ分布、Gumbel分布、Exponential分布、Log-normal分布等都是描述极值统计分布的经典理论模式[20],采用上述4种分布函数对年最大值法选取的样本进行分布拟合,并计算了不同历时降雨量的科斯检验值、相关系数与相对误差(表 1). 4种分布函数对各历时降雨量的拟合较好,不同历时的科斯检验结果均通过了95%的信度检验(<0.19),尤其是Pearson-Ⅲ分布和Log-normal分布对各历时的科斯检验结果基本在0.1以下,且相对误差较小(小于0.1),并具有很高的相关性.
图 2为60,1 440 min Pearson-Ⅲ分布和Log-normal分布的理论分布和实测分布图.可以看出理论值和实测值排列紧密,没有较大的偏差,Pearson-Ⅲ分布拟合效果明显比Log-normal分布要好.如图 2a中,40~60 mm对数正态分布拟合偏大,61~80 mm偏小,而Pearson-Ⅲ分布拟合接近实测频率密度. 图 2b中,75~150 mm对数正态分布拟合偏小,151~260 mm偏大,同样Pearson-Ⅲ分布拟合接近实测频率密度. 120,180,360,540和720 min拟合效果与图 2相类似(图略),均是Pearson-Ⅲ分布拟合效果好于Log-normal.利用Pearson-Ⅲ分布拟合各历时降水量重现期的可能极值,得到重庆主城区各历时降水量的重现水平,也就是各历时不同重现期的设计暴雨量(表 2).
-
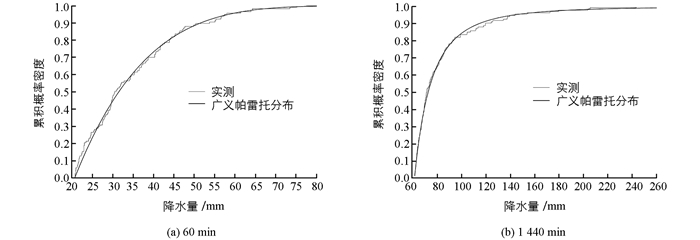
短历时强降水作为随机变量具有一定的不确定性,超过城市雨水排除系统设计标准的短时强降水,有的年份可能出现多次,有的年份可能一次也不会出现.年最大值法每年取一个最大值会遗漏一些数值较大的暴雨,丢掉一些有用信息,而GP分布是根据给定的门限值(即临界值)筛选样本序列中的极值所建立的超过该门限值的极值概率分布,这种抽样方法所拟合的分布模式更加符合实际[21].根据年多个样法,选取每年前8个最大值,拟合其GP分布,参照文献[21]方法对GP分布参数进行估计,通过拟合效果比较,选择科斯检验值和相对误差小、相关系数高的最佳门限值(表 3),并进行重现期的推算(表 4).
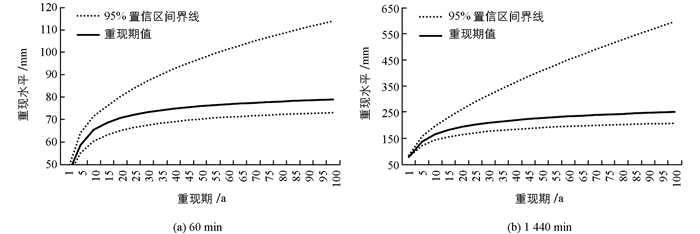
由表 3可见,重庆市主城区沙坪坝站各历时降雨量GP分布拟合结果的科斯检验值较小,计算的实测频数与理论频数的相关较好,相关系数均在0.98以上,相对误差基本小于0.05. 图 3为60 min和1 440 min的GP分布理论与实测累积频率分布曲线,可见,GP分布的理论累积概率曲线与实测累积频率曲线基本吻合.通过GP分布结果的重现期水平图(图 4)得出,推算的重现期都在置信区间内,表明GP分布方法对不同重现期下不同历时降雨量的估算结果可信.
-
《室外排水设计规范》(GB50014-2006,2014版)推荐设计暴雨量采用城市暴雨强度公式计算. 表 5为采用修订后的重庆市沙坪坝单一重现期暴雨强度公式计算的不同历时重现期设计暴雨量.
-
一般来说,设计暴雨量必须符合当地的气候特征. 1961-2013年沙坪坝站1 440 min最大降水量为271 mm(2007年7月17日),是当地有气象记录以来的最大值,中国气象局认为该次区域降水为重庆115年来最大降水,并被评为当年该月全国八大罕见极端气候事件之一[22-23].但从暴雨强度公式计算的不同历时重现期设计暴雨量来看(表 5),1 440 min 100年与50年重现期设计暴雨量为314.2和282.3 mm,按此标准计算,2007年7月17日的降水量还未达到50年一遇,这与实际气候特征不符.其原因是由于重庆主城区暴雨强度公式编制所用资料比本文短,资料年限为1981-2013年,且只采用了5,10,15,20,30,45,60,90和120 min历时资料,未采用大于2h的历时资料.虽然各历时1961-2013年资料包含1981-2013年,但理论极值特征反映的是序列极值的平均特征,受样本随机性影响大[24],加之1961-2013年与1981-2013年变化趋势各不相同(图 1),以致两时段推算的设计暴雨量相差较大.
使用1981-2013年各历时资料,采用与沙坪坝站暴雨强度公式编制相同的频率分布曲线,得到1981-2013年推算的设计暴雨量(表略),其中60,120 min设计暴雨量与表 5相同,但与表 4相比,2,3,5,10,20,30,50和100年重现期平均偏大10.8%,14.2%;180,360,540,720和1 440 min与暴雨强度公式计算值相比(表 5),在2,3,5,10年重现期平均偏小-28.4%,-20.8%,-13.6%,-5.3%,在20,30,50,100年重现期平均偏大2.4%,3.7%,5.1%,7.2%.可见,在使用《室外排水设计规范》(GB50014-2006,2014版)推荐的采用暴雨强度公式计算设计暴雨量时,应注意暴雨强度公式编制时使用的资料年限与历时.
由表 1可见,年最大值法选样拟合中,Pearson-Ⅲ分布拟合效果最好,下面将Pearson-Ⅲ分布与GP分布拟合结果进行比较.从设计暴雨量来看(表 2、表 4),两种方法拟合的不同历时重现期设计暴雨量比较接近;但从拟合效果来看(表 1、表 3),Pearson-Ⅲ分布拟合各历时平均科斯检验值、相关系数、相对误差分别为:0.08,0.90,0.05,GP分布为:0.06,0.99,0.04.可见,GP分布的拟合效果要好于Pearson-Ⅲ,GP分布推算结果可信度更高.
从GP分布拟合的不同历时重现期设计暴雨量可以看出(表 4),60,1 440 min从2年至100年重现期设计暴雨量分别为46.1~79.0 mm,93.9~251.1 mm,从实际降水来看,1961-2013年60,1 440 min最大雨量出现时刻为1983年8月28日23:27~28日0:26、2007年7月16日19:37~17日19:36,实测降雨量为80和271 mm,均超过了百年一遇.与实测资料的对比,GP分布拟合的不同历时重现期设计暴雨量符合重庆市主城区的气候特征.
通过GP分布拟合的不同历时重现期设计暴雨量(表 4)与重庆地区现行水文重现期标准[25]进行对比,1 440,60 min各重现期降雨量标准基本一致,360 min百年一遇值偏大10 mm,各历时重现期设计暴雨量符合实际排水设计要求.
2.1. 各历时降雨量变化特征
2.2. 年最大值法选样的概率分布
2.3. 年多个样法选样的概率分布
2.4. 暴雨强度公式计算
2.5. 结果比较
-
1) 1961-2013年重庆市主城区60,120,180,360,540,720,1 440 min年最大降雨量呈增加趋势,高值主要集中在20世纪70年代中后期至80年代初期、2000年以来至今.
2) 采用Pearson-Ⅲ分布、Gumbel分布、Exponential分布、Log-normal分布对年最大值法选取的样本拟合均在0.05水平检验分析上具有统计学意义,其中Pearson-Ⅲ分布拟合效果最好,但与GP分布对年多个样法选取的样本拟合效果相比,GP分布的拟合效果更好,精度更高.如使用1961-2013年资料推算设计暴雨雨量,推荐使用GP分布拟合的设计暴雨量.
3) 如用户所需设计暴雨量的历时是该地暴雨强度公式编制采用的历时之一,且资料年限一致,则可使用暴雨强度公式计算设计暴雨量,否则将会造成误差.
4) 不同工程勘查设计对不同历时强降水概率分布函数拟合结果的要求不同,在使用时应视具体情况而定.值得注意的是,短历时强降水是自然界中一种复杂随机变量,加之每种概率分布函数对不同数据都有其适用性,拟合推算的设计暴雨量只是在一定可信度条件下的一种带有置信区间的估计,会产生一些不确定性.由于气候变化具有显著的阶段性特征,降水资料本身存在明显的年代际变化,随着重庆主城区城市化建设进程加快,当各历时有新的降水极值出现时,须对设计暴雨量重新进行推算.



 下载:
下载: