通过查阅大量文献资料，确定出用于评价道路通行能力的7个常用评价指标，分别为：车道数目、道路等级、车流量、平均车速、平均行程时间、平均延误时间和平均排队长度，具体指标名称及指标内涵见表 2.

为了用这些指标评价小区开放对周边道路通行的影响，建立基于因子分析的道路通行能力评价模型.首先对7个评价指标进行因子分析，以利用较少个数的假想变量反映原来众多指标的主要信息，并给出各个假想变量的权重，得到最终关于道路通行能力的综合评价得分.

步骤1 选择分析变量对其原始数据进行标准化处理.

选取车道数目c₁、道路等级c₂、车辆数量c₃、平均车速c₄、平均行程时间c₅、平均延误时间c₆和平均排队长度c₇等7个指标作为分析变量.为消除量纲影响，先通过MATLAB编程对原始数据进行标准化处理.

设第i个路段的第j个指标的取值为a_ij，i=1，2，…，9，j=1，2，…，7).将各指标值a_ij转化成标准化指标 ${{{\tilde{a}}}_{ij}}$ ，有

其中：

即μ_j，s_j为第j个指标的样本均值和样本标准差，并记标准化之后的指标为c_i(i=1，2，…，7).

由拉依达准则法，如果实验数据值的总体是服从正态分布的，将有

式中，μ与σ分别表示正态总体的数学期望和标准差.此时，在实验数据值中出现大于μ+2σ或小于μ-2σ数据值的概率是很小的.因此，根据“小概率事件实际不可能性原理”，将大于μ+2σ或小于μ-2σ的实验数据值视为异常值.由于经过Z标准化方法处理后的数据应该满足正态分布，故将Z标准化后小于-2或大于2的样本数据视为异常值.观察标准化处理之后的数据可以知道，所有的数据都是非异常数据.这说明了收集到的数据是非常可靠的，可以用来进行后续的模型建立.

步骤2 计算相关系数矩阵R_cor.

相关系数矩阵，有R_cor=(r_ij)_7×7，有

其中：r_ii=1，r_ij=r_ji，r_ij是第i个指标与第j个指标的相关系数.

经过MATLAB编程求解可得相关系数矩阵

从相关系数矩阵中可以看出：车道数目与道路等级呈显著负相关、与平均延误时间呈显著正相关；车流量与道路等级呈负相关，与平均延误时间呈正相关；平均行程时间与平均车速呈显著负相关；平均延误时间与平均排队长度基本无关.

步骤3 计算初等载荷矩阵.

通过MATLAB编程求解，计算相关系数矩阵R_cor的特征值λ₁≥λ₂≥…≥λ₇≥0，及对应的特征向量μ₁，…，μ₇，其中μ_j=[μ_1j，μ_2j，…，μ_7j]，则可得初等荷载矩阵

步骤4 选择m个主因子.

根据初等荷载矩阵，通过MATLAB计算各个公共因子的贡献率，并选择m个主因子.对提取的因子荷载矩阵进行旋转，得到得到矩阵Λ₂=Λ₁^(m)T(其中Λ₁^(m)为Λ₁的前m列，T为正交矩阵).构造因子模型为：

在本模型中，通过MATLAB编程计算求得前3个主因子的累计贡献率达到93.17%，故在此选取前3个主因子.旋转后的因子贡献及贡献率见表 3、因子载荷见表 4.

由旋转因子分析表可知：变量c₁，c₂，c₃在T^TF₁上有较大载荷，而在其他旋转因子上的载荷较小或可以忽略；变量c₄，c₅，c₇在T^TF₂上有较大载荷，而在其他旋转因子上的载荷较小或可以忽略；变量c₆在T^TF₃上有较大载荷，而在其他旋转因子上的载荷较小或可以忽略.

因此，可称F₁为流量因子，称F₂为交通通达度因子，称F₃为延误时间因子.

步骤5 计算因子得分，并进行综合评价.

用回归方法求单个因子得分函数：

记第j个因子得分的估计值为

则有

且

其中： ${{\mathit{\boldsymbol{X}}}_{0}}={{\left( {{{\tilde{\alpha }}}_{ij}} \right)}_{19\times 7}}$ 是原始数据的标准化数据矩阵；R_cor为相关系数矩阵；Λ₂是步骤4中得到的荷载矩阵.

计算得各个因子得分函数为：

综合因子得分公式为

最后算出的综合因子得分越高，说明道路通行能力越强.

由综合因子得分公式和因子得分函数的系数可知：

1) 流量因子对道路通行能力的影响力＞交通通达度因子对道路通行能力的影响＞延误时间因子对道路通行能力的影响；

2) 车道数目和道路等级的改变，会造成综合得分的较大改变；

3) 车道数目和道路等级改变引起的综合得分的改变，远大于平均车速引起的综合得分的改变.

设某小区开放前，其周边某条道路通过基于因子分析的道路通行能力评价模型算出的综合得分为F，该小区开放后这条道路通过基于因子分析的道路通行能力评价模型算出的综合得分为F′，则最终的该小区开放对这条路的影响评价值为：

其中 ${sgn} =\left\{ \begin{array}{*{35}{l}} 1 & \text{当}x>0\text{时} \\ 0 & \text{当}x=0\text{时} \\ -1 & \text{当}x＜0\text{时} \\ \end{array} \right.$

根据α的取值，可将开放该小区给这条道路带来的影响分为3种情况：

1) 若α＞0，则开放该小区给这条道路带来的影响是有利影响，且α越接近于1，说明影响越有利；

2) 若α＜0，则开放该小区给这条道路带来的影响是不利影响，且α越接近于-1，说明影响越不利；

3) 若α=0，则开放该小区给这条道路带来的影响几乎没有，且α越接近于0，说明影响越微弱.

具体的α的取值范围对应的影响评价见图 1.

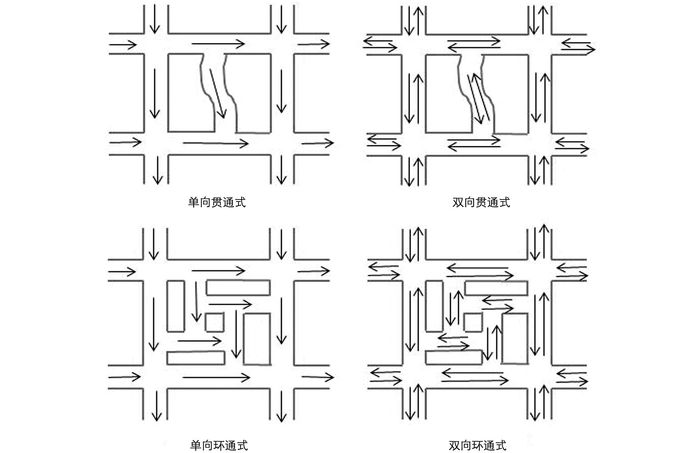
本研究主要以居住区内道路的形态为主要因素，将小区划分成不同的类型.从形态方面来看，居住区内基本呈现3种形态：贯通式、环通式和尽端式.但尽端式的小区，由于其自身结构，即使开放，也会因不能起到连通作用而不能提高周边道路的通行能力.故在此仅考虑贯通式和环通式两种小区内部道路形态.同时，每种形态的道路，又可按照车辆通行方向分为单向通行道路和双向通行道路.也就是说，根据小区内部道路形态的不同，可将小区分成4种类型(图 2).

在这4种小区中，单向贯通式小区与双向环通式小区较典型，故选取这两种小区类型，利用VISSIM软件进行模拟仿真，其具体思路是：通过构建车辆通行环境(道路网、交通控制条件、限速条件等)、驾驶员行为(跟车、换道超车等)、车辆性能特性、需求产生特性等交通要素的计算机模型，“再现”或“预演”交通流在不同的交通流组织方案和交通控制管理方案下的运行特性，达到评价和优选道路交通设施设计、管理方案的目的.

在平面剖分图的部分分两次分别放置单向贯通式小区和双向环通(内向双环)式小区，输入3 000车流量进行模拟，得到综合评价所需指标数据.通过仿真模拟，可得开放两种类型小区前后各路段平均车速、平均延误时间、平均行程时间和车辆数量的对比折线图(图 3-图 6).

从开放两种类型小区前后各路段平均车速对比图(图 3)中可以看出：

1) 当小区周边道路的车道数目为2时，无论开放单向贯通式小区还是内向双环式小区，都会对主干道车速起到消极的影响；

2) 当小区周边道路的车道数目为4且道路级别为快速路时，开放单向贯通式小区，可以在一定程度上提升主干道的车速；

3) 小区周边道路的车道数目越多，开放小区给主干道上车速带来的影响越小.

从开放两种类型小区前后各路段车辆数目对比图(图 5)中可以看出：

1) 无论哪种小区，无论小区周边道路的车道数目和道路等级如何，将小区开放，都会在一定程度上降低主干道上的车流量；

2) 小区周边道路的车道数目越多，开放小区给主干道上车流量带来的影响越大；

3) 无论周边道路车道数目和道路等级如何，开放单向贯通式小区和开放内向双环式小区给主干道上车流量带来的影响都非常接近.

从开放两种类型小区前后各路段平均行程时间对比图(图 6)中可以看出：

1) 无论周边道路车辆数目和道路等级如何，开放小区都会在一定程度上增加主干道车辆的平均行程时间，且开通内向双环式小区造成的平均行程时间提升大于开通单向贯通式小区造成的平均行程时间提升；

2) 开放小区所提升的车辆平均行程时间，会受到周边道路的车道数目和道路等级的共同影响，比如当周边道路为次干道且为4条车道时，开放两种类型的小区造成路段车辆平均行程时间的提升几乎可以忽略；

3) 周边道路等级越高，开放单向贯通式小区和内向双环式小区造成的路段车辆平均行程时间的提升差异越小.

从开放两种类型小区前后各路段平均延误时间对比图(图 6)中可以看出：

1) 开放单向贯通式小区，几乎不会对各路段的平均延误时间造成影响，但开放内向双环式小区会造成平均延误时间的大幅度提升；

2) 当周边道路为次干道、车道数目为4，以及周边大陆为支路，车道数目为3时，开放内环双向式小区给平均延误时间带来的影响几乎可以忽略.

综合图 3-图 6的折线图，研究各类型小区开放前后对道路通行的影响问题，可以得到以下结论：

1) 虽然开放小区会造成主干道上的车流量减少，但也可能造成主干道上的车速降低、平均行程时间提升和平均延误时间提升；

2) 当小区周边路段车道数目较多时，可优先于小区周边路段车道数目较少的情况开通小区；

3) 在车道数目较适中、道路级别为主干道时，开通单向贯通式小区比开通内向双环式小区更合适；

4) 在车道数目较多、道路级别为次干道时，可考虑开通单向贯通式小区.