高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

CR网络中基于最优阈值选取的攻击感知算法

,  , 

上一篇

下一篇

王会, 余阳, 李旭伟. CR网络中基于最优阈值选取的攻击感知算法[J]. 西南大学学报（自然科学版）, 2018, 40(4): 132-138. doi: 10.13718/j.cnki.xdzk.2018.04.018
引用本文: 王会, 余阳, 李旭伟. CR网络中基于最优阈值选取的攻击感知算法[J]. 西南大学学报（自然科学版）, 2018, 40(4): 132-138. doi: 10.13718/j.cnki.xdzk.2018.04.018
shu
Hui WANG, Yang YU, Xu-wei LI. An Attack Perception Scheme Based on Optimal Threshold Selection in Cognitive Radio Networks[J]. Journal of Southwest University Natural Science Edition, 2018, 40(4): 132-138. doi: 10.13718/j.cnki.xdzk.2018.04.018
Citation: Hui WANG, Yang YU, Xu-wei LI. An Attack Perception Scheme Based on Optimal Threshold Selection in Cognitive Radio Networks[J]. Journal of Southwest University Natural Science Edition, 2018, 40(4): 132-138. doi: 10.13718/j.cnki.xdzk.2018.04.018
shu

CR网络中基于最优阈值选取的攻击感知算法

  • 1.

    成都东软学院 计算机科学与工程系，成都 611844

  • 2.

    成都东软学院 信息管理系，成都 611844

  • 3.

    四川大学 计算机学院，成都 610064

  • 基金项目: 国家自然科学基金项目(60902038)；四川省教育厅项目(14ZA0366，18SB0028)；教育部高等教育司项目(201701004019)
详细信息
    作者简介:

    王会(1978-)，女，四川成都人，硕士，副教授，主要从事网络信息安全、软件工程等方面的研究 .

  • 中图分类号: TN929.5

An Attack Perception Scheme Based on Optimal Threshold Selection in Cognitive Radio Networks

  • 1.

    Department of Computer Science and Engineering, Chengdu Neusoft University, Chengdu 611844, China

  • 2.

    Department of Information Management, Chengdu Neusoft University, Chengdu 611844, China

  • 3.

    College of Computer, Sichuan University, Chengdu 610064, China

  • 摘要: 由于认知无线电(Cognitive Radio，CR)网络允许多个未知无线设备接入频谱，使其存在模仿主用户攻击(Primary User Emulation Attack，PUEA)的安全隐患，为此，提出一种具有攻击感知能力的协作感知方案.首先，在授权主用户信号频谱资源处于占用和空闲这2种情况下，估计PUEA伪信号出现的概率；然后，利用得到的估计参数确定最小化总误差概率的最优阈值；最后，融合中心通过感知报告与阈值来判断主用户信号是否存在，以达到感知模仿主用户攻击的能力.仿真试验结果表明：与最优用户选择(Optimal User Selection，OUS)方法相比，提出的方法在应对主用户仿真攻击时具有更好的安全性能，提高了CR网络的安全效能.
    Abstract: Cognitive radio (CR) networks allow multiple unknown wireless devices to access the spectrum, which often makes the networks vulnerable to primary user emulation attacks (PUEA). Aiming at the problem, a novel cooperative sensing scheme with attack-aware capability in the presence of a malicious PUEA is proposed. First, the probability of the occurrence of PUEA pseudo-signals is estimated in two cases, where the licensed user spectrum resources are occupied or idle. Then, the parameters obtained are used to determine the optimal threshold that minimizes the total error probability. Finally, the fusion center can use the sensing report and the threshold to determine whether a primary user signal is present, so as to have the ability to sense a PUEA attack. Simulation results indicate that compared with the method of optimal user selection, the proposed method has better safety against PUEA and improves the performance of CR networks.
  • 加载中

  • 图 1  CR网络系统模型

    下载: 全尺寸图片 幻灯片

    图 2  攻击参数的收敛曲线

    下载: 全尺寸图片 幻灯片

    图 3  虚警概率，漏检概率，误差概率与阈值的关系

    下载: 全尺寸图片 幻灯片

    图 4  误差概率与平均信噪比γ的关系曲线

    下载: 全尺寸图片 幻灯片

    图 5  ρ=0.1时误差概率与平均信噪比γ的关系曲线

    下载: 全尺寸图片 幻灯片

    图 6  ρ=1时误差概率与平均信噪比γ的关系曲线

    下载: 全尺寸图片 幻灯片

    图 7  ρ=10时误差概率与平均信噪比γ的关系曲线

    下载: 全尺寸图片 幻灯片
  • [1] 郑元兵, 朱韵攸, 王灿, 等.基于线性价格机制的多认知无线网络资源配置框架[J].西南大学学报(自然科学版), 2016, 38(6): 172-179. doi: http://xbgjxt.swu.edu.cn/jsuns/jsuns/ch/reader/view_abstract.aspx?file_no=201606028&flag=1
    [2] 贺欢欢, 王兴伟, 黄敏.认知无线电网络的一种演化博弈频谱共享机制[J].系统仿真学报, 2016, 28(3): 756-763. doi: http://www.cnki.com.cn/Article/CJFDTotal-XTFZ201603034.htm
    [3] 王凯, 卢为党, 郭淑琴, 等.基于功率分配的双向协作频谱接入方法[J].西南师范大学学报(自然科学版), 2015, 40(8): 92-98. doi: http://edu.wanfangdata.com.cn/Periodical/Detail/xnsfdxxb201508018
    [4] 申滨, 王舒, 黄琼, 等.基于Gerschgorin圆盘理论的认知无线电宽带频谱感知[J].通信学报, 2014, 35(4): 1-10. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-TXXB201404001.htm
    [5] 刘永姣. 认知无线电中基于能量检测的频谱感知技术研究[D]. 天津: 南开大学, 2012.
    [6] SHEN L, WANG H, ZHANG W, et al. Multiple Antennas Assisted Blind Spectrum Sensing in Cognitive Radio Channels[J]. IEEE Communications Letters, 2012, 16(1): 92-94. doi: 10.1109/LCOMM.2011.110711.111901
    [7] 曾昆, 彭启航, 唐友喜.基于信任节点辅助的安全协同频谱感知策略[J].信号处理, 2011, 27(4): 486-490. doi: http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_xhcl201104002
    [8] 曹开田, 王东林.模拟主用户攻击情况下的压缩宽带频谱感知[J].仪器仪表学报, 2015, 36(1): 167-173. doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yqyb201501021
    [9] 李方伟, 冯德俊, 朱江.一种基于PUE恶意干扰的认知无线电态势感知方案[J].电信科学, 2013, 29(12): 21-27. doi: http://www.cqvip.com/QK/91166X/201409/662559477.html
    [10] CHEN R, PARK J M, REED J. Defense Against Primary User Emulation Attacks in Cognitive Radio Networks[J]. IEEE Journal on Selected Areas in Communications, 2008, 26(1): 25-37. doi: 10.1109/JSAC.2008.080104
    [11] 申滨, 王舒, 黄琼, 等.认知无线电最优用户选择协作频谱感知[J].北京邮电大学学报, 2014, 37(2): 32-37. doi: http://www.oalib.com/paper/4161784
    [12] CHEN C, CHENG H, YAO Y D. Cooperative Spectrum Sensing in Cognitive Radio Networks in the Presence of the Primary User Emulation Attack[J]. IEEE Transactions on Wireless Communications, 2011, 10(7): 2135-2141. doi: 10.1109/TWC.2011.041311.100626
    [13] 杨天鸿. 认知无线电网络中的基于信道特征的主用户仿真攻击防御技术[D]. 杭州: 浙江大学, 2012.http: //cdmd. cnki. com. cn/article/cdmd-10335-1012312462. htm
    [14] 杨建新. 认知无线电网络抵御恶意模拟主用户攻击方法的研究[D]. 昆明: 云南民族大学, 2015.http: //cdmd. cnki. com. cn/Article/CDMD-10691-1015429829. htm
    [15] DIGHAM F F, ALOUINI M S, SIMON M K. On the Energy Detection of Unknown Signals Over Fading Channels[J]. IEEE Transactions on Communications, 2007, 55(1): 21-24. doi: 10.1109/TCOMM.2006.887483
    [16] MA J, ZHAO G, LI Y. Soft Combination and Detection for Cooperative Spectrum Sensing in Cognitive Radio Networks[J]. IEEE Transactions on Wireless Communications, 2008, 7(11) : 4502-4507. doi: 10.1109/T-WC.2008.070941
  • 加载中
图( 7)
计量
  • 文章访问数:  1023
  • HTML全文浏览数:  671
  • PDF下载数:  54
  • 施引文献:  0
出版历程
  • 收稿日期:  2017-06-20
  • 刊出日期:  2018-04-20

CR网络中基于最优阈值选取的攻击感知算法

    作者简介: 王会(1978-)，女，四川成都人，硕士，副教授，主要从事网络信息安全、软件工程等方面的研究
  • 1. 成都东软学院 计算机科学与工程系，成都 611844
  • 2. 成都东软学院 信息管理系，成都 611844
  • 3. 四川大学 计算机学院，成都 610064
  • 收稿日期:  2017-06-20
基金项目:  国家自然科学基金项目(60902038)；四川省教育厅项目(14ZA0366，18SB0028)；教育部高等教育司项目(201701004019)

摘要: 由于认知无线电(Cognitive Radio，CR)网络允许多个未知无线设备接入频谱，使其存在模仿主用户攻击(Primary User Emulation Attack，PUEA)的安全隐患，为此，提出一种具有攻击感知能力的协作感知方案.首先，在授权主用户信号频谱资源处于占用和空闲这2种情况下，估计PUEA伪信号出现的概率；然后，利用得到的估计参数确定最小化总误差概率的最优阈值；最后，融合中心通过感知报告与阈值来判断主用户信号是否存在，以达到感知模仿主用户攻击的能力.仿真试验结果表明：与最优用户选择(Optimal User Selection，OUS)方法相比，提出的方法在应对主用户仿真攻击时具有更好的安全性能，提高了CR网络的安全效能.

English Abstract

    全文HTML

  • 无线通信服务的快速增长带来了严重的频谱短缺问题，认知无线电(Cognitive Radio，CR)的引入很好地解决了这一问题[1-3].在CR网络中，次级或非授权用户仅在对授权主用户(Primary User，PU)的操作不产生干扰的前提下，才被允许使用属于授权主用户的空闲频段.而频谱感知方法用于检测CR网络中的PU信号，存在一系列不确定性问题[4].为了缓解各种衰减问题[5-6]，一般采用协同频谱感知方法(Cooperative Spectrum Sensing，CSS).在CSS中，每个用户独立进行局部感知，随后向融合中心报告测量值.基于接收数据的性质，融合中心选择一个软性或硬性的组合规则以确定信道状态.然而，CR网络架构具有允许多个不同的未知无线设备伺机接入频谱的特性，使得CR网络存在严重的安全隐患[7].例如一些恶意用户通过伪造发射参数和仿真信号从而伪装成一个授权主用户，造成其他CR用户无法正常接入信道，此类攻击被称为模仿主用户攻击[8-9].由于模仿主用户攻击较为常见且破坏大，如何抵御模仿主用户攻击，提高网络的安全性能一直是CR网络的研究热点.

    如文献[8]提出了一种基于位置的防御机制，利用PU信号发射机的物理位置信息和接收信号强度特征进行信息验证.文献[9]讨论了在不使用任何位置信息的情况下抵御模仿主用户攻击的方法，该方法首先基于Fenton近似法推导恶意用户信号接收功率的概率密度函数，然后提出Neyman-Pearson复合假设检测法和Wald序贯概率比检测法，以检测恶意用户.文献[10]研究了一种不同于以上方法的协同频谱感知方案.首先在融合中心对不同CR用户的感知信息进行加权组合；然后，对分配的权重进行优化，以最大化虚报警率进行概率检测.然而，该方案假设模仿主用户攻击在广播环境中始终存在，不符合实际，且造成的能耗更大.文献[11]研究无线信道的特征参数，从用户中独立提取信道特征参数，基于硬判决联合检查方法对发射机身份进行验证，抵御攻击者发起模仿主用户攻击，即最优用户选择(Optimal User Selection，OUS)的协同频谱感知.文献[12]基于改进的能量检测算法和软融合策略推导系统的检测概率和虚警概率之间的关系，在虚警概率一定的情况下，求出最优加权系数矩阵，利用该矩阵抑制PUEA信号.

    现在的大多数研究均是假设PU发射机的物理位置或特有性质等先验信息对于CR用户或融合中心是已知的，但很多时候这些信息并非完全知晓[13-14].为此，本文提出误差概率最小化的阈值选取(Threshold Selection of Minimizing Error Probability，TSMEP)方案，该方案对PU信号发射机的物理位置或特定属性的先验信息不做任何要求.每个CR用户检测其自身的频谱感知，并将测量值发送到融合中心；然后，计算感知测量值的第一阶距和第二阶距，完成2个攻击参数的估计，2个攻击参数分别表示PU信号存在和不存在时，模仿主用户攻击信号的出现概率，通过使用该攻击参数确定能够最小化总误差概率的最优阈值.

1.   系统模型

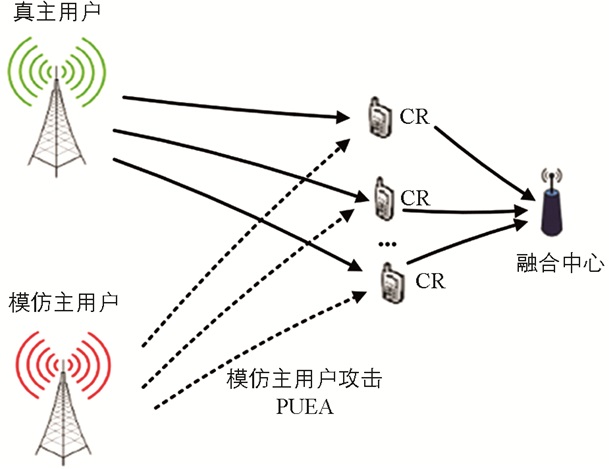
  • 本文采用集中式CR网络系统模型，如图 1所示，包括一个PU发射器、N个CR用户、一个融合中心和一个恶意PUEA发射器.模型假设：N个CR用户随机分布在一个较小的区域内，与PU发射器、PUEA发射器相距较远；同时该PUEA能够精确区分分配给主用户的占用频段和空闲频段.

    按照PU和PUEA信号是否存在的情况，有4种可能状态，具体表示如下：

    Hs0：只存在噪声；

    Hs1：PU+噪声；

    Hs2：PUEA+噪声；

    Hs3：PU+PUEA+噪声.

    第一种状态Hs0出现于CR用户仅接收到噪声的情况下，信道没有被PU或者PUEA信号占用；第二种状态Hs1出现于PU在信道上发射信号且不存在PUEA信号的情况下；第三种状态Hs2表示不存在PU信号且PUEA发射伪装信号，CR用户只能接收到PUEA信号加噪声；最后一种状态Hs3表示同时存在PU信号和PUEA信号.

    本文设定H1和H0分别表示PU信号存在与不存在的2种情况，Eon和Eoff表示PUEA信号存在与不存在的2种情况.基于该种假设，每种可能状态Hsk的概率表示为πk，设参数α和β分别为2个假设情况H1和H0中存在PUEA伪信号的条件概率，即

    其与攻击者的策略相关联.则有：

    对于4种可能状态，第j个用户的第i个样本的接收信号xji可表示为

    其中，nji为第j个CR用户的加性高斯白噪声；参数 $\sqrt {{\gamma _j}} p_j^i$ 和 $\sqrt {{\gamma _j}} e_j^i$ 分别为接收到的能量为γj和λj的PU信号和PUEA信号.本文假设每个nji样本、PU信号pji和PUEA信号eji的噪声均服从独立高斯分布(μ=0，σ=1).同时假设CR用户经过具有相同平均信噪比的独立分组衰减信道.由于CR用户远离PU和PUEA信号发射器，因此，γj和λj随着观察周期的不同而改变，其概率密度函数分别服从均值为γ和λ的指数分布.定义参数ρ=λ/γ表示攻击强度，较大的ρ值(ρ≥1)表示一次强度较大的PUEA.综合式(2)和上述假设，则接收到的信号xji为高斯分布：

    对每个CR用户使用M个样本进行局部能量检测，根据中心极限定理[15]，如果样本数目较大，可假设第j个用户的能量Ej为高斯分布，能量Ej表示如下：

    在CSS中，每个CR用户的局部能量测量值被发送到融合中心，用来对PU信号的存在与否情况进行全局判断.不存在PUEA时，用传统的等增益合并方法[16]计算所有感知报告的总和，并与一个预设阈值相比较.如果报告的总和超过阈值，则该信道被确定为占用状态；反之，为空闲状态.

    通常情况下，PUEA通过向广播环境中发送伪信号欺骗CR用户，以阻止CR用户接入空闲频段，因此可通过对攻击者的分析提出适当的频谱感知规则.设Qfa为CSS中的全局虚警概率，则

    Qm表示全局漏检概率，则

    式中，Don和Doff分别表示融合中心判定PU信号存在和不存在的情况.

    传统方法不考虑PUEA能量，本文定义总误差概率Qe评价存在恶意PUEA情况时CSS的性能.参数Qe表示PU信号检测中作出错误判定的概率，即融合中心判断存在PU信号而实际上并不存在，或融合中心判定不存在PU信号而实际上存在的情况.总误差概率可以表示为

    结合式(1)、式(5)和式(6)，式(7)可变为：

2.   本文攻击感知算法

    2.1.   攻击参数估计

  • 本小节基于接收到的感知测量数值对P(H0)和P(H1)中攻击参数α和β进行统一估计. E(Ej)和E(Ej2)分别为接收到的感知测量值的均值和二阶距，通过式(4)可以得出：

    其中，

    从而有

    考虑到瞬时信噪比γj和λj的指数分布，可得出

    和

    将式(1)代入式(10)和式(12)，有

    式中的参数Ψ0，Ψ1，Ψ2，Ψ3，φ0，φ1定义如下：

    从式(13)中可知，未知攻击参数α和β的数值为

    满足

    下面将对α和β函数的最优阈值进行计算.

    • 2.2.   最优阈值计算

  • 首先，确定不存在PUEA信号(α=β=0)情况下的最优检测阈值.若不存在PUEA信号，将不会出现Hs2和Hs3这2种状态(π2=π3=0).因此，全局误差概率Qe为状态Hs0和Hs1检测时的误差概率.则式(8)为

    利用如下公式求取最小化误差概率Qe的最优阈值η*：

    当PUEA存在时，分别在ρ≤1和ρ＞1两个不同条件下计算最优阈值.

    对于ρ≤1，式(8)中的全局误差概率Qe可表示为

    则最优阈值η*为

    式中的函数F(·)为正态分布的概率密度函数，

    对于式(18)，可利用数值计算方法求取最优阈值η*.

3.   仿真实验结果和分析

  • 本文提出的系统模型中，假定一个检测间隔中共有8个CR用户(N=8)，样本数M=20；信道为分组衰减；已知PU和CR用户间的平均信噪比γ，以及PUEA和CR用户间的平均信噪比λ；先验概率P(H0)和P(H1)分别为0.8和0.2.通过超过10 000轮的蒙特卡洛仿真得出结果.

    为了体现所提方案的优异性，将文献[11]视为对照组.文献[11]从用户中独立提取信道特征参数，基于硬判决联合检查方法对发射机身份进行验证，即最优用户选择OUS的协同频谱感知.本文提出的误差概率最小化的阈值选取TSMEP方案，其特点是对PU信号发射机的物理位置或特定属性的先验信息不做任何要求. 2种方案均考虑了不同的攻击参数和不同的阈值选择情况，如最优阈值和非最优阈值等情况.

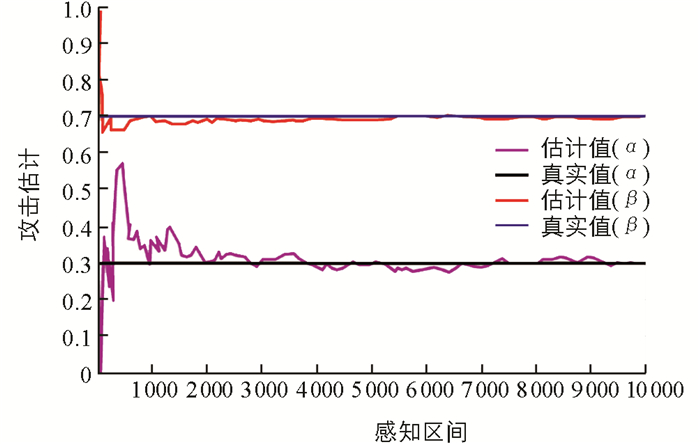
    攻击参数α=0.3，β=0.7时的收敛情况如图 2所示.在进行大约1 000和2 000轮感知测量后，α和β的估计值分别收敛至常数. P(H1)=0.2，α=0.3意味着PUEA在假设情况H1中仅有30%的概率发射伪信号，α的收敛性小于β的收敛性.在仿真中，前2000个感知间隔可设为初始阶段，对攻击参数进行估算，之后寻找最优阈值，以提高恶意PUEA存在的情况下CSS的性能.

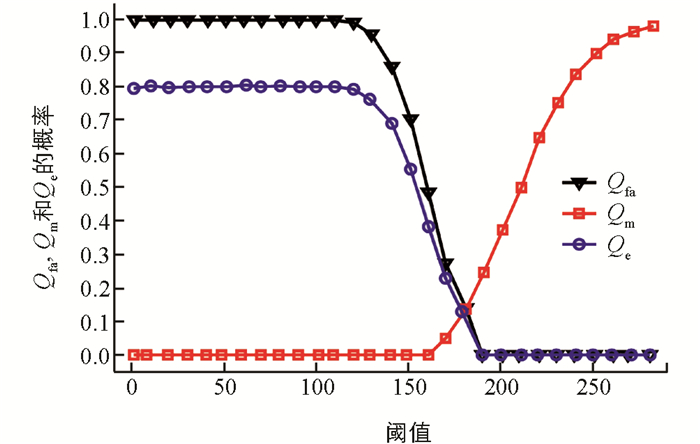
    在没有PUEA伪信号时，虚警概率Qfa、漏检概率Qm和误差概率Qe与决策阈值的函数曲线如图 3所示.平均信噪比γ为-5 dB，阈值变化范围为0~270.可以看出，Qfa随着阈值的增加而降低. Qm与Qfa相反，Qm随着阈值的增加而增加.根据图 3中显示的Qe的形状和Qe最小值存在的特性，可以验证在最优阈值η*处存在最小误差概率Qe.

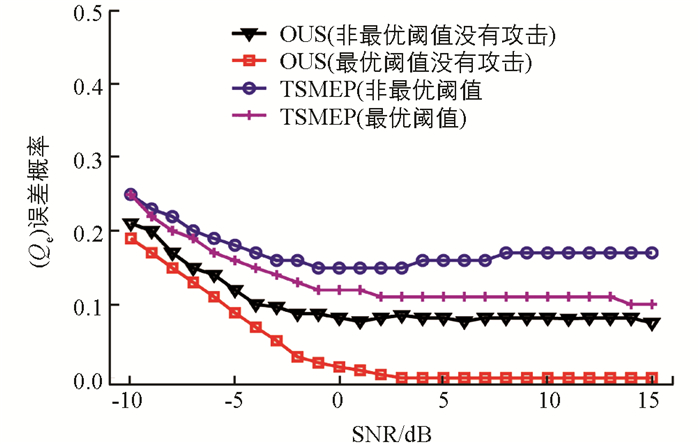
    在不存在攻击和存在攻击的2种情况下，融合中心利用最优阈值和非最优阈值时，其总误差概率Qe随着平均信噪比γ的变化情况如图 4所示.其中，攻击强度ρ设定为0.5；非最优阈值通过将式(8)中的总虚警概率设为常值0.1获得.对比最优阈值和非最优阈值选取方法的误差概率，文献[11]提出的OUS主要是研究无线信道的特征参数，从用户中独立提取信道特征参数，是一种最优用户选择的CSS.从图 4可以看出，最优阈值方法的误差概率更低.本文的所有后续仿真实验均选取最优阈值.

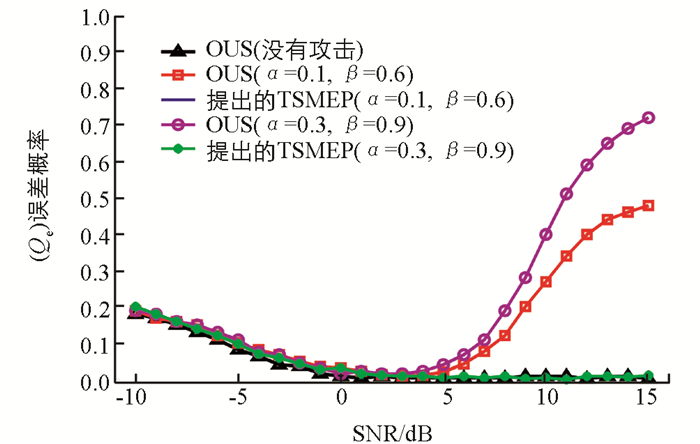
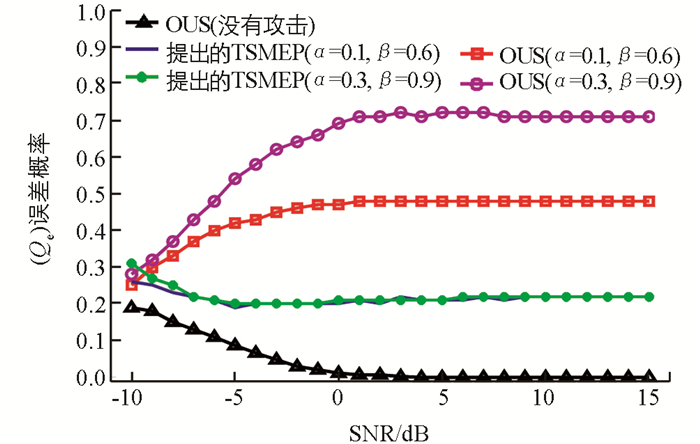
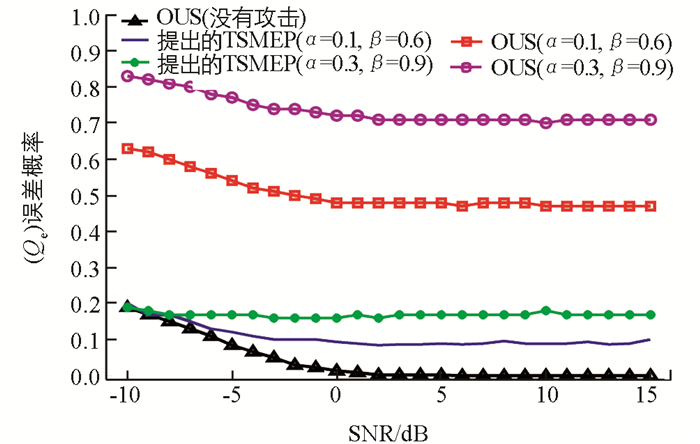
    当攻击强度ρ为0.1，1和10时，误差概率Qe与平均信噪比γ的关系曲线如图 5~图 7.当ρ=0.1时，本文提出的TSMEP方法有效地抵御了PUEA的破坏性影响.在ρ=1的情况下，本文方法的误差概率也没有超过0.2.通过与文献[11]的OUS技术相比，本文提出的TSMEP方法显著提高了CSS抵御恶意PUEA信号攻击的性能.

4.   结论

  • 本文通过对协同频谱感知进行研究，在阈值选取方法的基础上，提出了一种可防御PUEA的协同频谱感知方案.该方案估计2个攻击参数，即存在和不存在PU信号时，PUEA伪信号出现的概率，并利用该参数确定最小总误差概率的最优阈值，使其可以在PU信号检测中得出较小的概率误差.仿真实验结果表明，提出的方案较传统方案更加安全有效.

参考文献 (16)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回