汽车平稳运行与有害气体低排放有赖于理想空燃比的控制，要将其精确地控制在理论空燃比附近存在诸多控制难点，如控制中氧传感器响应存在迟滞性，空燃比反馈控制的响应时间长，因此难以实时正确地反馈空燃比；由于存在动态的充排气现象，导致按照进气量计算出的喷油量出现偏差；进气管内油膜动态特性可能引起油膜蒸发进入气缸和蒸气直接进入气缸，导致空燃比变化；由于喷油过程在进气过程之前，节气门在开关过渡过程中，进气流量可能发生较大变化，因此时间顺序也可能造成空燃比变化等等.导致上述产生空燃比变化的现象是多种多样的，但是从控制论角度剖析其机理，可将其归纳为燃烧过程具有不确定性复杂过程的控制论特性，这正是传统控制面临的挑战^[4-6].表现在：①燃烧过程难以进行数学描述与建模，燃烧过程复杂度高，结构化程度差，具有显著的半结构与非结构特征，影响燃烧的不确定性因素众多.尽管文献[7]对天然气发动机空燃比的自适应控制进行了研究，但是该文并未涉及燃烧过程的数学建模型问题. ②反映燃烧状态的变量之间存在关联耦合，关系错综复杂，难于通过状态解耦变换为单变量的简单控制. ③燃烧过程的强非线性特性因其受不确定性因素影响难于进行量化处理. ④燃烧过程参数呈现参数时滞的未知性与时变性. ⑤燃烧过程与运行状况有关，由于运行所处环境复杂多变，受外部环境干扰影响，运行状态的切换具有极大的不确定性.针对上述控制论特性，传统方法(无论基于经典还是近代控制理论的方法)因受控制器结构的固定约束与控制功能的局限性不可能实现对燃烧过程的理想空燃比控制.

燃烧过程的不确定性导致过程参数与过程模型结构在一个大范围内变化，难以事先预测，因此其控制过程属于病态结构，传统控制策略很难通过对燃烧过程的控制实现期望的理想空燃比.从传统控制角度考虑，理想空燃比的控制本身就是一个理想运动轨迹的过程跟踪问题，但是传统控制系统的输入与输出不接受非数量形式的信息数据，缺乏解决高度非线性等控制问题的有效手段，也难以与外部环境进行信息交换，因此传统控制对不确定性复杂燃烧过程控制是无能为力的.随着人工智能和自动控制理论的发展，智能控制为理想空燃比控制提供了可供参考借鉴的控制策略^[8-10].智能控制是一种无须人工干预就可自主地驱动智能控制器达到期望控制目标的自动控制技术，其中特别值得指出的是仿人智能控制器.仿人智能的控制策略基于人类智能对事物的观察、学习、理解和认识，直观地模仿人类的控制行为，采用产生式规则描述人类对事物的观察、学习、理解、认识、启发与直觉推理和控制行为，即采用条件语句“If condition Then action”表达人类的推理过程和控制行为，仿人智能可以从仿人决策过程与仿人控制功能两个方面体现.人类决策是分层次的，不同层次的决策机制与决策机构所处理的信息抽象程度是不同的，感兴趣的信息也有所不同，文中涉及的属于底层相关控制数据信息处理，因此可通过总结现场实际操作者与控制专家对被控燃烧过程特性的控制经验、控制技巧与智慧，借助产生式规则描述其获得的直觉推理结论和应采取的控制行为，基于在线特征辩识与特征记忆就可以抽象出燃烧过程的误差特征模型与动态特征模型，再将开闭环控制和定性决策与定量控制相互融合，构成基于仿人智能的融合控制策略与多模态控制算法对被控过程实施控制.对燃烧过程而言，如果空燃比偏离理想值，就必须通过直接或者间接方式对其过程施加控制使空燃比恢复到理想值状态.

图 1为基于多模态控制算法的广义控制模型. 图 1中，r(t)，e(t)，P(t)与y(t)分别表示控制系统输入、系统误差、智能控制器输出与控制系统输出.

在基于HSIC的基本控制模态中，仅有两种类型的控制模型态：

① 如果e$ \dot e $≥0与e+$ \dot e $≠0成立，那么可以采用比例-半微分控制模态，即P-HD(proportion-half derivation)控制模态，智能控制器输出为

② 如果e·$ \dot e $＜0或者|e|+|$ \dot e $|≤δ成立，那么可以采用半开环控制模态，即HO(half open-loop)控制模态.智能控制器输出为

在上述两种控制模态中，

其它数学符号的意义为：$ {\dot e} $，${\ddot e} $分别为系统误差的一阶与二阶导数，e_m，i为系统误差的第i个极值，e_m，n为第n次系统误差极值，k_p为比例系数，k为抑制系数，$ \overline{{{P}_{n}}} $为智能控制器输出P第n次需要保持的值.定义：P₀≜0(极值记忆误差)，P_HD为P-HD控制模态输出信号P的半微分分量，$ {\dot e} $_m，i为P-HD控制模态中误差变化率${\dot e} $的第i个极值，$ \widetilde P $_l为P-HD控制模态中P_HD半微分输出分量第l次需要保持的常数值.定义：$ \widetilde P $₀≜0(误差极值记忆)，i，l，n分别为自然数，δ为智能控制器的灵敏度阀值.

基于HSIC的原型控制算法为

该控制算法对不同的控制模态采用不同的控制策略，交替地使用两种控制模态，就可实现对被控燃烧过程开、闭环控制相结合的多模态控制.如果e·$ \dot{e} $＞0∪e=0$ \dot{e} $≠0，则采用比例控制模态；如果e·$ \dot{e} $＜0∪$ \dot{e} $=0，则采用保持控制模态.在融入人类调节技巧、实际控制经验、专家知识与操作者的智能以及智慧后，针对具有不确定性燃烧过程的融合控制算法可采用结构化英语描述方法如下.

If e·$ \dot{e} $≥0 and $ \dot{e} $≠0 Then

If $ \dot{e} $·$ {\ddot{e}} $≥0 Then

If $ \dot{e} $·$ \ddot{e} $＜0 Then

If (e·$ {\dot{e}} $＜0 OR|e|+|$ {\dot{e}} $|≤δ) Then

If|e|≥$ \frac{1}{2} $|e_m，n|＞δ Then

Else P(t)=P_n

上述控制算法融合了人的智能，模仿了人的思维过程，其显著优点在于控制器设计者对燃烧过程无需更多的先验知识，该算法构成的控制系统鲁棒性强，响应速度快，对系统误差变化的灵敏度高，因此其控制精度高.

由于燃烧过程复杂，受到多种不确定性因素的影响，比如含氧量检测存在的迟滞性、动态充排气现象导致的喷油量偏差、进气管内油膜动态特性引起空燃比变化以及进气流量在节气门开关过渡过程中可能发生的变化等，为了方便仿真并不失一般性，可将不确定性因素影响等效为过程参数变化对过程响应的影响.由于含氧量检测具有时间滞后特性，为了仿真实验对比研究有说服力，文中选取Smith预估PID最优控制器作为比较参照算法，因为该算法对时间滞后有良好的补偿效果.此外，为了观察过程响应的细微变化，在仿真实验中的时间尺度人为地加大，将时间尺度放大到秒的量级.假设燃烧过程模型为具有时间滞后特性的二阶模型，即燃烧过程传递函数为

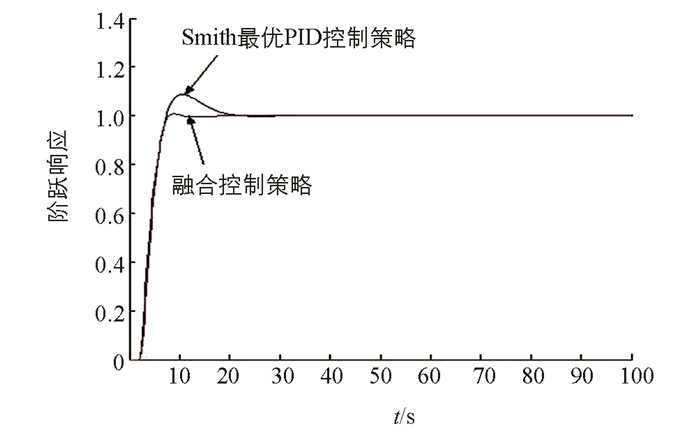
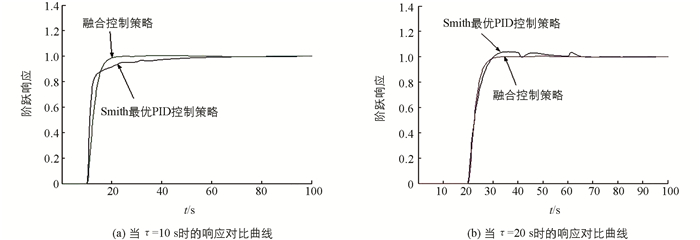
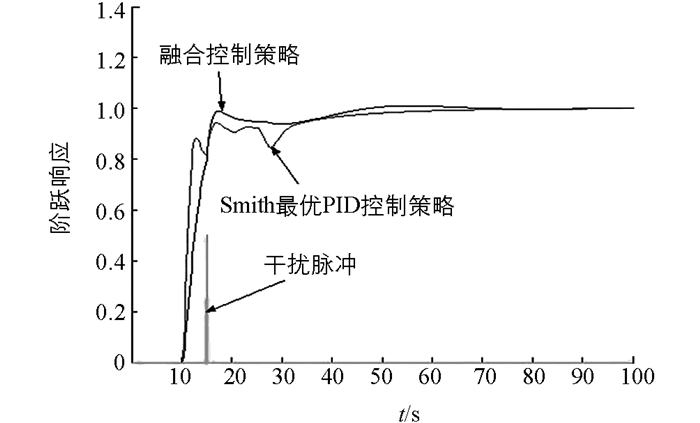
在仿真实验中，时间滞后τ分别选取为τ = 2 s，τ = 10 s和τ = 20 s，在单位阶跃输入条件下，采用Smith最优控制与融合控制策略的过程响应分别如图 2、图 3(a)和图 3(b)所示.图中，纵坐标为系统的单位阶跃响应，是无量刚的相对比较量；横坐标为时间，单位为s. 图 4是时间滞后为τ = 10 s时在15 s时刻加入一个外部扰动干扰(脉冲宽度0.2 s，脉冲幅度0.5)的过程响应.

分析图 2到图 4的过程响应曲线可知，无论过程响应的快速性、跟踪特性与过程响应的超调量指标，还是抗外部脉冲干扰能力，在控制性能方面融合控制策略都优于Smith最优控制器.过程响应的仿真结果显示，基于智能融合的控制策略有更强的鲁棒性能，在调节过程中不会产生超调，响应速度快，调节时间短，跟踪特性更好，受外部扰动时抗干扰能力强.

上述针对发动机燃烧室的控制论特性，探讨了一种燃气发动机空燃比的融合控制策略.基于仿人智能融合控制与Smith最优PID控制算法的仿真对比研究表明，融合控制策略优于Smith最优PID控制策略，过程响应速度快、调节时间短、过程响应无超调与抗外部脉冲干扰能力强，因此对燃气发动机空燃比控制，选取融合控制策略是合理与可取的.