-
电网运行是否正常影响着国家的发展和人民的生活.农网电力公司的供电辖区架空线路大多是沿山地架设,穿越树竹林,线路因“手拉手”率小,绝缘化率较低,抵御外力能力和转移负荷能力均较弱,特别是在迎峰度夏期间,出现风雷暴极端恶劣天气的频率较高且持续的时间较长;高压输电线路通道内的树竹随着时间的增加而不断地生长,相对于电网线路的树竹缺陷概率增加,虽有人工蹲守、群众护线以及通道砍伐等应对措施,但还是引发了大量线路跳闸和95598投诉.现有统计数据显示:大风雷暴等极端天气产生树竹刮蹭裸导线引发线路故障数占总故障次数的67.39%,说明现有的应对措施很难达到理想的效果,同时还消耗了大量的人力和财力.
树竹是国家不可缺少的资源,国家退耕还林和封山育林的政策鼓励大面积的树竹种植与再生,使输电线路在运维通道方面增加了大量的人力、物力和财力.要解决树障问题,同时兼顾到国家利益总体达到最优,可以对树竹生长高度建立一个预测模型,预测到树竹的生长高度将会对线路通道产生影响时,再消除树竹缺陷.有关树竹的生长模型的研究报道较多,时明芝等人[1]在2005年对107杨树阳性冠幅与胸径关系进行了研究,其线性相关系数达到93.99%;张杰伟[2]在2010年对合肥市常见的三类植物(香樟、广玉兰、女贞)分别利用Logistic方程、Gompertz方程、Richards方程、Weibull方程以及S曲线5种模型进行生长模型分析;刘伟琪等人[3]在2013年考虑影响树木生长规律因素,通过对园林树木种植密度分析来构建树木的生长模型;杨楠等人[4]在2017年利用树木的生长模型结合监控设备,对树木生长高度进行预测,对输电线路可能造成的威胁进行预警,从而保证输电线路的正常运行.
由于早期研究时期计算机技术较为落后,国外学者对运维智能评估和评级的研究仅限于运用聚类分析、因子分析以及相关分析等统计学知识.比如,1936年Fisher[5]、1941年Durand[6]根据判别分析方法划分优次等级对信用等级进行了评价.在判别分析进入了评级领域后,更多的先进实用的分类评级技术竞相出现,国外学者开始从大量数据中提取特征来分析行为并作出分类以及预测模型.随着预测模型的出现和发展,决策模型渐渐浮出水面,在1973年,Mangasarian[7]提出递归分割法,递归分割法是将总体样本进行分割再预测结果.在国外学者研究的基础上,国内也逐渐开始了对数据智能评估评级的研究,近10年当中,周晖等人[8]在2007年利用Logistic回归模型识别电力客户欠费概率大小,以以往的客户资料作为数据,根据Logistic回归模型预测欠费的可能性,即输出结果为有欠费风险与无欠费风险,从而减少客户欠费风险.除Logistic模型对数据评级之外,马立新等人[9]在2018年利用K近邻算法对能效指标评级,其过程为筛选能效指标,确定分级,交叉检验选择k值,最后利用模型评估电力用户等级.本研究利用主成分分析得出影响运维质量的3个主要因素,再Logistic回归模型,根据树竹缺陷预测数、缺陷消缺率和资金的合理使用度3个因素评价其运维质量.
本研究的设想是筛选影响架空线路运维质量的树竹缺陷、缺陷消缺数和运维资金使用度3个主要因素,然后根据树竹生长的规律建立一个树竹生长高度预测模型,预测树竹的生长高度,根据高度和树竹与架空线路的水平距离给定一个阈值,预测结果超出这个阈值,就认为是树竹的一个缺陷,根据树竹预测的缺陷数,树竹缺陷的消缺数和资金使用的合理度,建立一个架空线路运维质量的智能评估系统,指导各个供电所按需分配运维资金,避免传统平均划拨运维资金,树竹缺陷密集的供电所运维资金不足,树竹缺陷少的供电所获得了大量的剩余运维资金;节省供电所传统派出人员进行树竹缺陷例行巡查的高成本和抢修抢险的费用,这种例行巡查可能导致了没有树竹缺陷也在巡查,有树竹缺陷却没有巡查或没有巡查到,产生不必要的差旅费用和高额的抢修抢险费用.根据本研究提出的智能评估系统进行评估,其结果可以指导各个供电所采用科学的方法消除数竹缺陷,尽可能地降低线路故障的发生概率,树立电网公司的优质服务形象.
全文HTML
-
影响架空线路运维质量的因素有:树竹生长高度x1、树障缺陷预测数x2、树竹引发故障抢修数x3、巡视人员数x4、15天内消除缺陷数x5、30天内消除缺陷数x6、高峰期投入资金数x7和低峰期投入资金数x8等,这些因素中有些是相关的,有些是相互独立的,为降低模型的识别难度,需要从这些因素中筛选出相互独立的主要影响因素,主成分分析能够用较少的变量去解释原来数据中的大部分差异,通常按照累计贡献率大于80%的原则选取主成分个数,再从主成分中选取权重较大的解释变量作为筛选的主要因素.
设架空线路的影响因素为x1,x2,…,x8,记为
$\mathit{\boldsymbol{X}} = \left( {\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}}\\ \vdots \\ {{x_8}} \end{array}} \right)$ ,将原始影响因素x1,x2,…,x8综合成8个主成分y1,y2,…,y8,记为$\mathit{\boldsymbol{Y}} = \left( {\begin{array}{*{20}{c}} {{y_1}}\\ {{y_2}}\\ \vdots \\ {{y_8}} \end{array}} \right)$ ,yi与x1,x2,…,x8的关系为:记
则主成分写成矩阵形式:
其中C为正交矩阵.
首先获取了8个变量x1,…,x8的270次观测数据的样本观测矩阵:
样本观测矩阵中xij(0)表示第i个变量在第j次的观测数据.为克服量纲的影响,需要将原始数据作标准化处理:
其中
样本观测矩阵的数据经过标准化处理以后,得到数据矩阵X:
主成分y1,y2,…,y8相互正交,270个样本点变换后在主成分y1上有最大的方差,在主成分y2轴上有次大的方差,…,在主成分y8轴上有最小的方差;同时不同的yi和yj轴的协方差为0,即
由于X是原始数据经标准化处理后的数据,XX′实际上是原始数据的相关系数矩阵R,即
于是得到
由此得到
即:
C′的第i列
$\left( {\begin{array}{*{20}{c}} {{c_{i1}}}\\ {{c_{i2}}}\\ {{c_{i2}}}\\ \vdots \\ {{c_{i8}}} \end{array}} \right)$ (或C的第i行向量的转置)就是相关系数矩阵R的特征值λi对应的特征向量,因此求x1,…,x8的主分量转化为求相关系数矩阵R的特征值和特征向量,y1方差为λ1,y2的方差为λ2,…,y8的方差为λ8,并且满足λ1≥λ2≥…≥λ8,将采集样本数据的相关矩阵的特征值计算的结果列于表 1.由于相关矩阵R的特征值λi度量了第i个主成分yi在270次观测中取值变化的大小,一般按选取累计贡献率大于90%的原则选取主成分个数.由于累积贡献率
所以取前3个主成分,而这3个主成分中树竹缺陷数、缺陷消缺数和资金合理使用度的权重最大,因此影响架空线路的主要因素是树竹缺陷数、缺陷消缺数和资金合理使用度.
-
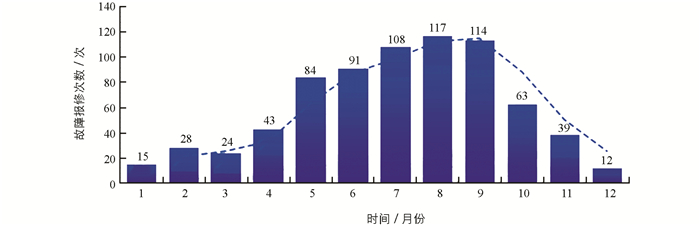
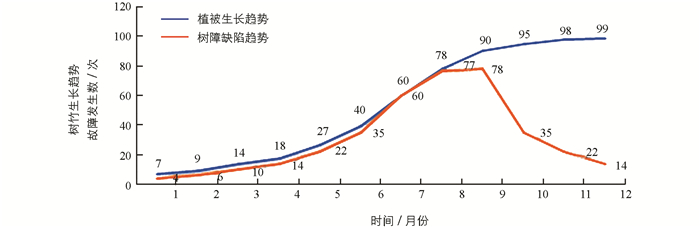
影响架空线路通道运维质量的主要因素是树竹缺陷数、缺陷消缺数和资金合理使用度3个因素,最主要的因素是树竹缺陷数.树竹的生长缺陷将会影响到架空线路的运维质量,一方面,架空线路正下方的树竹长到一定的高度会影响线路的正常运行;另一方面,当架空线路周边的树竹长到一定的高度时,在大风雷暴等极端天气将产生树竹刮蹭裸导线而引发高架线路故障.因此需要对架空线路的树竹高度和架空线路周边的树竹生长高度分别给出阈值,树竹生长高度超过给定的阈值,即可认为树竹生长产生缺陷.为避免公司频繁地派出众多的人员进行巡视,可为树竹生长高度建立一个预测模型,预测树竹生长的缺陷数.树竹的生长与很多因素有关,不同品种树竹的生长规律有一定的差异,即使是同一个品种的树竹,在不同的土壤肥沃程度、二氧化碳浓度、光照温度、树竹的间距和行距等生长条件下,其生长规律也有差异,应该建立树竹的高度与土壤肥沃程度、二氧化碳浓度、光照温度、树竹的间距和行距的多元线性回归模型[10],但要采集到这些数据涉及到很多的部门,部门之间的数据存在壁垒,不能共享.因此在缺失环境数据的情况下,本研究根据树竹生长的高度与时间的关系规律采集样本数据,根据采集到树竹生长规律的样本点分布来看,树竹生长规律与S型生物生长曲线相吻合,也与实际情况吻合.正常情况下,春季温度较低,植被开始生长,其生长速度较慢,规模不大,对架空线路的影响不大;随着温度的升高,植被生长达到旺盛期,其中以6月到9月的生长速度最快,达到一定的规模与高度,这时对架空线路的影响较大,在9月份因树竹刮蹭裸导线引发的故障报修数达到最大值;进入冬季后,植被生长基本停止,极端恶劣天气减少,树竹不容易刮蹭到电线,且在10月之前消除了大部分故障,砍去了对架空线路有较大影响的树竹障碍,因此10月之后的故障数呈下降趋势.以月份为横轴,以月度树竹生长高度和故障发生数为纵轴,得到树竹生长与缺陷引发线路故障的联合趋势分布图(图 1).
一年的实际情况如图 2所示,说明图 1的一年故障趋势图与实际报修故障数有良好的一致性.
由图 1可以看出:树竹生长高度呈现出S型曲线,可以用曲线
进行拟合,其中hi表示第i个月份树竹的高度.
为了估计模型的参数,将原方程变形得到
作变量代换:
(1) 式变为:
对采集的样本训练数据集T={(e-1,y1),(e-2,y2),…,(e-n,yn)},采用最小二乘法得到模型参数的估计式:
表 2中的缺陷预测数是模型预测出的缺陷数,缺陷消缺率是各个供电所消除缺陷数的比例,故障抢修数是各个供电所抢修高架线路的故障数,从表 2可以看出,在这一年中仍然有抢修故障存在,这主要是由于各个供电所的树竹生长缺陷没有消缺完,也可能是预测产生的误差.因此还需要对各个供电所的消缺工作进行评估,督促消缺工作做得差的供电所加强消缺工作,提高架空线路的运维质量.
-
运检PMS2.0系统内树竹缺陷预测数据、巡视到位的数据及消除缺陷数据,再采集营销SG186系统里架空线路故障报修数据、财务管控系统内的通道运维专项资金数据,可对各个供电所的架空线路运维质量进行评估.
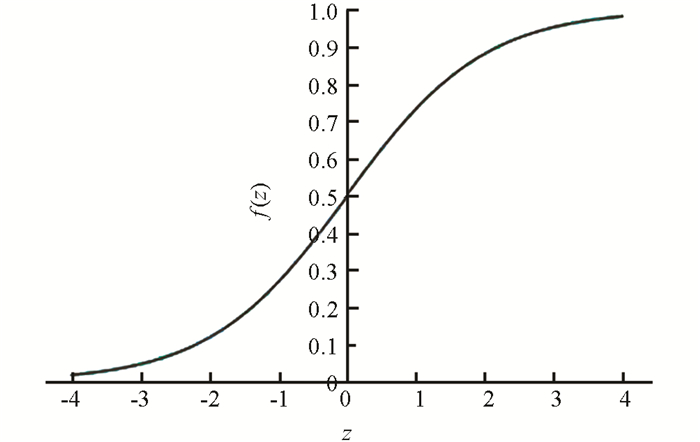
影响架空线路运维质量的有树竹缺陷预测数、缺陷消缺率和资金的合理使用度3个因素,预测准确度、消缺率和资金使用合理度较高,架空线路报修的概率就越小,若3个指标与植被生长趋势、故障报修分布趋势、资金合理使用度趋势相同,架空线路的运维质量就比较好,这可以用逻辑回归的Sigmoid函数进行刻画[11]. Sigmoid函数为
其图像见图 3.
Sigmoid函数的函数值在区间(0,1)内,图像也呈S曲线型,与树竹的生长规律相当吻合,用它来评价线路通道的运维质量比较客观[12].首先将树竹生长缺陷预测数x1、消缺率x2、通道运维资金使用合理度x3综合成一个综合指标z,xi的权重记为ωi,ωT=(ω1,ω2,ω3),XT=(x1,x2,x3),得到综合指标的表达式为
把采集的綦南电网公司的数据,以分成两类为例说明评级的方法.以每年报修10次以下作为好,报修10次以上作为差.权重ωi的估计采用极大似然估计,记:
极大似然函数为
两边取对数,得
由于l(ω)是负值,所以引入代价函数
利用梯度下降法,求使得代价函数J(w)最小的参数wi,
所以得到权重更新的公式为:
把綦南电网公司2017年的17个供电所随机抽取了13个供电所(总量的80%)的数据作为训练集,利用梯度下降法迭代500次,得到树竹缺陷巡视到位率、消缺率、通道运维资金合理使用度对应的权重系数(ω1,ω2,ω3)=(21.491,1.141,2.448),由此得到:
其Wald统计量均通过检验(α<0.05),表明该模型有统计学意义.
由此得到对各个供电所的架空线路的运维质量评价类别为:
(2) 式表示把z值代入p(Y=1)和p(Y=0)的表达式,计算这两个概率值,若p(Y=1)值大,则判别该供电所对架空线路归属于好,若p(Y=0)的值大,则判别该供电所对架空线路归属于差[13].
为检验本研究给出的分类模型的正确性,把采集的綦南电网公司剩下的供电所1.供电所7,供电所14和供电所17的数据作为测试集,预测结果和实际评级结果见表 5.
由表 5可以看出:只有供电所7的架空线路的质量评为好,其他3个供电所的运维质量评为差.
供电所7的巡视到位率和资金的使用度与理想程度的相似度较高,导致故障报修次数较少,线路正常运转的质量概率较高,故障报修次数只有8次,这主要是由于巡视到位率和消缺率也没有达到100%所引起的,但相对于其他供电所运维质量还是比较好的;
供电所1和供电所17的巡视到位率都非常低,巡视到的缺陷数与预测的缺陷数有较大的差异,可以理解为巡视人员巡视工作不细致,敷衍了事,没有消缺的缺陷数导致线路故障的发生;消缺资金的使用与理想的消缺资金使用相似程度太低,运维资金的使用存在较大的漏洞,缺陷没有及时消除,故障报修次数较多,产生高额的抢修抢险费用;
供电所14虽然资金使用相似度较高,主要是巡视到位率较低,没有巡视到的树竹缺陷导致架空线路故障的发生.
从回归模型z=-22.532+21.491x1+1.141x2+2.448x3的权重可以看出:巡视到位率的权重(21.491)最大,说明巡视到位率对架空线路通道运维质量评估结果的影响程度最大,其次是消缺资金使用的合理度的权重(2.448),最后是消缺率的权重(1.141),因为消缺率是由供电公司统一布置,巡视到位的树竹缺陷基本上消除了,只是消除缺陷是否及时的问题.
-
本研究运用科学的统计分析方法筛选出影响架空线路的主要影响因素,为树竹的生长建立了一个恰当的预测模型,从而得到树竹生长的树竹缺陷数[14];利用Sigmoid函数为架空线路的运维质量构建了一个评价模型,对各个供电所的架空线路运维质量进行评价,指导各个供电所提高运维质量;将根据树竹生长模型预测出的树竹生长缺陷数作为巡查树竹缺陷数,然后根据树竹缺陷数,合理地划拨运维消缺资金,再根据树竹生长规律,集中消缺树竹缺陷数,尽可能保持高架线路的畅通,减少因线路的运维质量较低所引发的故障数.为了验证本研究模型及算法的有效性,将本研究建立的模型于2018年试用于重庆市綦南电网公司,公司故障抢修工单比2017年下降18.79%,95598停电投诉比2017年下降27.63%,抢修抢险费用比2017年下降24.76%.本研究提出的智能评估模型为电力公司的架空线路管理提供了基于数据的决策模式,模型兼具安全性、创新性、经济性以及可推广性,实现了“用数据管理企业、用信息驱动业务”的目标.



 下载:
下载: