-
知识图谱(knowledge graph)是一种揭示实体之间关系的语义网络,可以对现实世界的事物及其相互关系进行形式化地描述[1],一般表示为三元组(头实体、关系、尾实体)的形式[2].如WordNet[3],Freebase[4]和YAGO[5]等将知识图谱广泛应用于问答系统、智能搜索和个性推荐等领域,但是很多大型开放知识图谱都是由人工或半自动的方式构建的,这些图谱通常比较稀疏,大量实体之间隐含的关系未被充分挖掘出来[6],因此知识图谱的补全方法成为新的研究热点.
表示学习是实现知识图谱补全的有效方法,它将知识图谱的实体和关系映射到连续的向量空间,利用向量计算方式推出实体之间潜在的语义关系,使得计算复杂度降低[7].表示学习中常用的两个模型是翻译模型和线性模型[8],其中翻译模型包括TransE模型[9]和基于TransE的一系列改进模型,如TransH模型[10]、TransR模型[11]和TransD模型[12]等.线性模型包括DistMult模型[13]、ComplEx模型[14]和ANALOGY模型[15]等,线性模型还具有良好的规则学习属性.但这两种模型对具有较少关系的实体(稀疏实体)表示效果较差[16],因为好的表示依赖于丰富的知识.规则学习也是知识图谱补全的重要手段,主要利用规则的演绎能力进行关系推演,可以保证结果的可靠性和可解释性.规则学习包括基于随机行走的规则挖掘[17-18]、知识图谱关联规则挖掘算法AMIE[19]及改进的AMIE+[20]等基于图结构的规则学习方法.这些方法虽然在结构上加快了推理速度[21],一定程度上缓解了规则学习的高复杂问题,但是仍存在规则搜索空间大、无法较好评估规则和仅考虑知识图谱结构等问题.
2019年,Zhang等人[22]提出了IterE模型,首次利用具有丰富语义OWL2中的对象属性表达公理进行演绎推理,有效提升了稀疏实体的表示效果和规则学习的效率.但该模型仅包含表示学习层和规则学习层,其泛化能力较弱,且模型中所采用的Frobenius范数计算方式复杂、无法显著区分高分公理.在航空安全事件知识图谱的研究方面,王红等人[23-24]研究了民航突发事件实体与关系的自动抽取方法,初步解决了航空安全事件知识图谱的构建问题,但未充分考虑实例层和概念层(本体)内稀疏实体之间隐含的语义关系.
为此,本研究提出一种改进的知识图谱补全方法(I_IterE),通过增加特征层和改进的评分机制获得高分公理进行演绎推理,旨在更好地利用高分公理进行演绎推理和链接预测,实现航空安全事件知识图谱的进一步补全,为基于知识图谱的航空安全事件语义分析提供更好的数据支持.
全文HTML
-
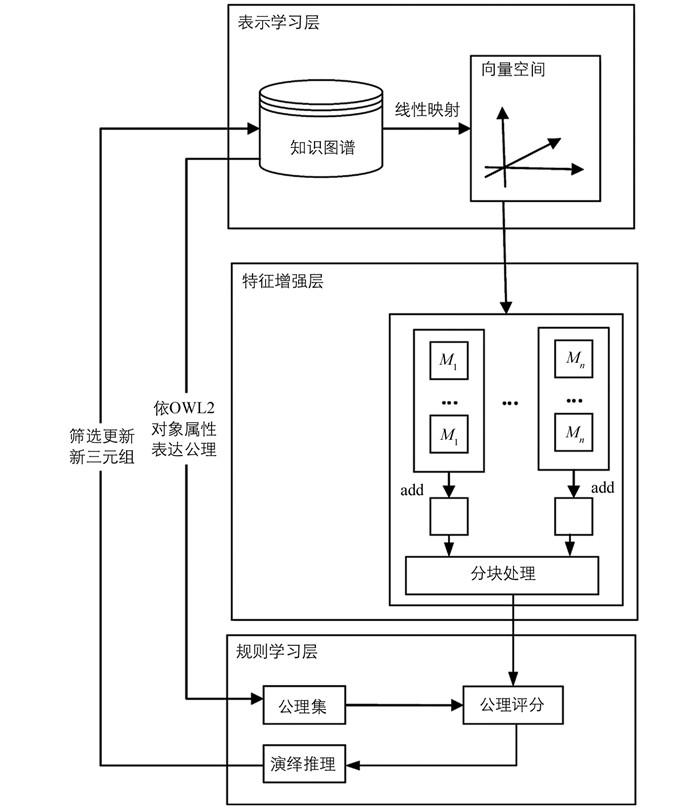
IterE模型包括表示学习层和规则学习层,通过表示学习层获得的关系特征,结合规则学习层挖掘的公理集,采用相应的评分机制获得高分公理进行演绎推理.为了提升模型的泛化能力和规则学习的效率,本研究提出的改进模型I_IterE(图 1). 图 1中:
(1) 表示学习层 利用线性模型将知识图谱中的实体和关系映射到向量空间中.
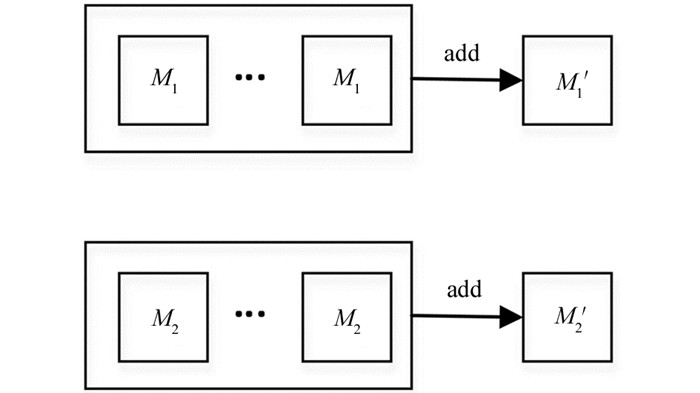
(2) 特征增强层 对表示学习层的关系特征利用add[25]方法对关系特征叠加从而增强特征.
(3) 规则学习层 将生成的公理集与增强后的关系特征采用改进的评分机制对公理进行评分,获得高分公理进行演绎推理,从而实现知识图谱的更新.
-
知识图谱可以描述为G={E,R,T},其中E为实体的集合,R为关系的集合,T={(h,r,t)|h,t∈E;r∈R}为三元组的集合.在三元组(h,r,t)中,h,r和t分别为头实体,关系和尾实体.表示学习层的输入集I表示为:
其中:lhrt是三元组的标签,用以评估三元组的可靠性;Taxiom是规则学习层生成的三元组;Tnegative是通过将(h,r,t)∈T的h或t随机替换为e∈E或者将r替换为r′∈R生成的负样本集.
若(h,r,t)∈T,则lhrt=1;若(h,r,t)∈Tnegative,则lhrt=0;若(h,r,t)∈Taxiom,则lhrt=π(h,r,t).其中π(h,r,t)是由公理演绎预测的标签值.
对于输入集I,采用交叉熵作为损失函数,即如
其中:n表示输入的三元组数量,φ(h,r,t)采用线性模型中表现较好的ANALOGY模型的得分函数,表示为
其中:Vh∈
${{\mathbb{R}}^{1\times d}} $ ,Vt∈${{\mathbb{R}}^{1\times d}} $ 是h和t的向量表示,Mr∈${{\mathbb{R}}^{d\times d}} $ 是r的矩阵表示,d是表示维度,σ是sigmoid函数.经过表示学习层之后,可得到实体特征的集合ε和关系特征集合
$\mathbb{R} $ . -
由于公理的评估以关系特征为基础,而演绎推理主要依据高分公理,因此关系特征具有重要意义.
泛化能力是指模型对于新鲜样本(测试集)的预测能力,提升模型泛化能力的方法包括使用更多的数据、数据过采样、修改损失函数、改进模型深度和权重惩罚等,本研究采用改进模型深度的方法,通过增加特征层来提升模型泛化能力.
特征增强的具体过程:以某一公理包括M1和M2两个关系特征的公理为例,为避免不同语义信息的关系特征混杂产生噪音影响公理的评估,采用add方法[25]对关系特征进行特征增强.如图 2所示,add方法将关系特征中元素对应相加,并且相加后特征维度不变,只是每一维下的信息量在增加,进而增强语义信息较强的区域,通过特征重用提升最终的链接预测结果.其中,关系特征层数的选择通过链接预测的结果来确定,层数为3层时可使模型链接预测结果达到最佳.由于ANALOGY模型获得的关系特征对角相等,经特征增强后仍相等,因而仅根据关系特征的某一对角的相关值进行计算即可,利用Python中的split函数对增强后的关系特征进行分块(分片)处理,可以获得代表整个特征的块对角特征,极大降低计算复杂度.
-
规则学习层包括公理集生成、改进的评分机制和演绎推理三部分.首先依据OWL2的7种对象属性表达公理挖掘出知识图谱中存在的公理集,之后结合特征增强层的关系特征和改进的评分机制对各公理进行评分计算,最后根据高分公理进行演绎推理.
-
OWL2中7种对象属性表达公理见表 1所述.
表 1中,r,r1,r2表示关系变量,x,x0,x1,x2,y,z表示实体变量.
将知识图谱每个关系γ∈R生成图谱中可能存在的公理主要分为3个步骤.
步骤1:生成带关系变量的公理ReflexiveOP(γ),SymmetricOP(γ),TransitiveOP(γ),EquivalentOP(γ,r′),SubOP(γ,r′),InverseOP(γ,r′)和SubOP(OPChain(r′,r″),γ),其中{r′,r″}需用知识图谱中实际关系来替换的关系变量.
步骤2:知识图谱中随机选择与γ有关的k个三元组(e′,γ,e″)∈T,将直接链接到e′或者e″的关系替换步骤1公理中的r′或r″,从而具体化步骤1的公理.
其中k应尽可能小,并使公理集能覆盖所有可能公理的概率高于公理覆盖阈值,k的约束条件为
其中:N是三元组(e′,γ,e″)∈T的数目,p为最小公理概率,存在概率大于p的公理为高可能性公理,t为公理覆盖阈值.因此在固定的p,t的情况下,k的最佳选择应该是方程
$f\left( N \right)=N-N{{\left( 1-t \right)}^{\frac{1}{{{p}^{N}}}}} $ 的上限.步骤3:在知识图谱中查找并统计每个公理的支持数,将支持数大于等于1的公理添加到公理集Ω.
由于输入的知识图谱是固定的,因此公理集Ω仅需生成一次.
-
在评分处理之前,首先将表 1中的规则用表示学习层学到的实体特征和关系特征进行表示,并归纳得出相关规则结论(表 2).
例如,对于公理InverseOP(hasWife,hasHusband),如果知识图谱中存在(Carl,hasWife,Mary),根据表 1的规则,可以推出另一个三元组(Mary,hasHusband,Carl).假设Mary,Carl,hasWife和hasHusband的表示分别为VMary,VCarl,MhasWife和MhasHusband,对于上述两个三元组,根据线性映射假设,可得到两个等式:VCarlMhasWife=VMary,VMaryMhasHusband=VCarl.依据上述等式可推出:MhasWifeMhasHusband=I,其中I表示单位矩阵,该等式表明仅与两个对应的关系特征有关,与具体的实体特征无关,因此可将其视为公理InverseOP(hasWife,hasHusband)的一般结论. 表 2给出了每个公理规则结论的详细信息.
表 2中V和M分别表示实体特征和关系特征,I是单位矩阵.
给定关系特征的集合
$ \mathbb{R}$ 和公理集Ω,评分机制是基于每个公理类型的规则结论为公理a∈Ω计算得分.以M1a=M2a的形式来表示规则结论,其中M1a和M2a是单个关系特征或两个关系特征相乘后的特征.由于规则结论是从理想的线性映射中得到的,但表示学习层学到的关系特征各不相同.因此,通过比较M1a和M2a之间的相似性对公理a进行评分.IterE模型采用Frobenius范数进行评分,其计算公式为
其中:d表示关系特征M1a和M2a的维度.表示学习层经ANALOGY方法学习后关系特征对角块矩阵相同,因此在(5)式中重复计算对角块特征,目的是增大关系特征之间相似与不相似的差距.但关系特征中各值均在[-0.01,0.01]范围内,关系特征之间的差距经平方后会被大幅度缩小,从而无法较好过滤低分公理.为此,改进评分公式为
其中:F′表示改进的Frobenius范数,sa′(F′)表示通过改进的Frobenius范数计算出公理a的得分. (6)式将(5)式中的平方换成常量线性乘法,因为在[-0.01,0.01]范围内,常量线性乘法比平方更能较好地增大高分公理与低分公理的差距,利于筛选,进而有效进行演绎推理.但是因不同类型的公理sa′(F′)值变化很大,因此需将sa′(F′)归一化,等到
其中:t是公理a所属的公理类别,smax′(t)和smin′(t)是公理集Ω中所有类型t的最大和最小得分. sa′∈[0, 1]是公理a的最终得分,sa′越高,公理a的可信度越高.
-
给定知识图谱G和公理集Ω,首先利用公理的演绎能力推出新三元组,并预测其标签,然后过滤掉与稀疏实体无关的三元组,最后将Taxiom更新到知识图谱中.
利用公理的基本形式进行演绎推理,如公式(8)所示.
其中(hi,ri,ti)∈T且i∈[1,n]而(ha,ra,ta)∉T需添加到知识图谱中.为了预测(ha,ra,ta)的标签,首先将(8)式转换为
基于t范数的模糊逻辑[26]对公式(9)进行计算,例如(h1,r1,t1)⇒(h2,r2,t2)的标签由三元组(h1,r1,t1)和(h2,r2,t2)的标签确定,这是通过逻辑表示符号⇒定义,且遵循逻辑与、或和非的逻辑定义:
其中:b和c是逻辑表达,π(x)是x的标签.基于上述条件,可通过(10)-(13)式计算任何规则的标签.例如ga:(h1,r1,t1)∧(h2,r2,t2)⇒(ha,ra,ta):
因此,可得到
将(7)式计算的公理a的得分sa′作为ga的标签,即π(ga)=sa′.知识图谱中存在的三元组标签依据表示学习层的标签进行标记.若(h,r,t)∈T,则π(h,r,t)=1.因此,对于任何类型的公理a,可知三元组(ha,ra,ta)的标签为:
通过高分公理推出一组新三元组的集合Taxiom={(ha,ra,ta)|ha∈Esparse or ta∈Esparse},其中Esparse表示知识图谱的稀疏实体的集合.实体的稀疏性为
其中:f(e)是实体作为头实体或尾实体出现在图谱中的频率,fmax和fmin是所有实体里出现在图谱中的最大和最小频率. r(e)∈[0, 1],若r(e)=0,则表示e是图谱中出现最频繁的实体;若r(e)=1,则表示e是图谱中出现频率最小的实体.当r(e)>θsparsity,将实体e作为稀疏实体,其中θsparsity是稀疏阈值.以此推出所有可能的新三元组后,并过滤掉与稀疏实体无关的三元组,可以实现知识图谱的更新.
-
实验采用WN18-sparse,WN18RR-sparse,FB15k-sparse和FB15k-237-sparse数据集[22],它们是由知识图谱补全常用的公开数据集WN18和FB15k生成的[17]. 表 3中给出了各数据集的实体、关系、训练集、验证集和测试集的数量.
表示学习层采用均匀分布U(-0.01,0.01)初始化实体和关系.规则学习层中的最小公理概率一般取p=0.5,公理覆盖阈值t=0.95,由(4)式可知每个关系选择的相关三元组的数量设置为k=6.对于公理演绎,评分高的公理更可靠且不易产生噪声,因此为每个数据集设置阈值θ为0.9,并将saxiom′≥θ的公理作为高分公理.
对于WN18-sparse和FB15k-sparse,最大训练迭代次数设置为100,而WN18RR-sparse和FB15k-237-sparse的最大训练迭代次数设置为150.采用Adam优化器[27],其优势能够在训练过程中自动调整恰当的学习率,使得模型能够较快收敛,并适用于解决包含高噪声或稀疏梯度的问题[28].结合表示维度d∈(100,200)和L1正则化权重λ∈{10-4,10-5,10-6},最终在验证集中表现最好的实验参数见表 4.
-
链接预测是对知识图谱中的实体或关系进行预测.链接预测实验采用平均倒数排名(MRR)的原始设置和过滤设置,Hits@1,Hits@3和Hits@10在过滤设置情况下的得分作为模型性能评价指标,通常较高的MRR或Hits@n表示具有较好的预测效果.
对比模型考虑了表示学习方法中翻译模型的经典模型TransE和线性模型DistMult,ComplEx,ANALOGY以及基础模型IterE. WN18-sparse,WN18RR-sparse,FB15k-sparse和FB15k-237-sparse在不同方法上的链接预测结果见表 5和表 6.
由表 5和表 6可知,在各个数据集上,I_IterE的链接预测结果均高于其他模型,并且与模型IterE相比,在Hits@1,Hits@3和Hits@10指标上,最低高出了1.0%,最高高出了3.4%,达到了较好的实验效果.表明增加特征层和改进的评分机制,有效提升了模型的链接预测效果.
-
规则学习的效率通过学习的时间评估,而规则学习的质量通过高质量规则(HQr)的数量及其所占挖掘出的所有规则的比例(%).规则的质量通常使用头覆盖率(HC)进行评估.对于规则rule的头覆盖率定义如公式(16)所示.
其中head(rule)(e,e′)={(e,r,e′)∈T,support(rule)是rule的支持度,并且将HC>0.7的规则视为高质量规则.
对比模型为规则学习中效果较好的AMIE+[20]和基础模型IterE[22],规则评估结果见表 7.
由表 7可知,I_IterE模型的规则学习效率均优于IterE模型和AMIE+模型,同时高质量的规则数量增加.实验结果表明,评分公式中的平方替换为常量线性乘法,降低了计算复杂度,筛选出较多的高质量规则.
1.1. 表示学习层
1.2. 特征增强层
1.3. 规则学习层
1.3.1. 公理集生成
1.3.2. 改进的评分机制
1.3.3. 公理演绎
1.4. 实验效果分析
1.4.1. 实验数据与参数设置
1.4.2. 链接预测
1.4.3. 规则评估
-
航空安全事件知识图谱的数据集来自航空安全事故调查报告2007-2020年的1 879个航空安全事件,共提取出8 830个实体、32种关系和20 000个三元组.将三元组按6:2:2比例分别抽取到训练集、测试集和验证集中.参照公共数据集的实验设置进行实验,选出在验证集中表现最好的链接预测结果.
-
步骤1:采用均匀分布U(-0.01,0.01)向量初始化表示航空安全事件知识图谱的实体和关系,再经ANALOGY模型训练得到较好表示知识图谱的实体特征的集合和关系特征的集合.
步骤2:按照1.2节所述方法,对知识图谱的关系特征进行特征增强,之后利用Python的split函数对新关系特征进行分块(分片)处理.
步骤3:依据OWL2的7种对象属性表达公理,按照1.3.1节的3个步骤挖掘航空安全事件知识图谱中可能存在的公理集.
步骤4:结合步骤2获得的关系特征和步骤3的公理集,采用1.3.2节改进的评分机制对各公理进行评分并归一化.
步骤5:从步骤4中筛选出大于等于0.9的高分公理推演出新三元组并根据公式(14)对三元组进行标记,并将新三元组中实体属于稀疏实体的保留,反之过滤.最后更新航空安全事件知识图谱.
-
将I_IterE模型应用于航空安全事件数据集进行链接预测,并通过MRR和Hits@n来反映实验效果,使用IterE模型与I_IterE模型进行比较,实验结果见表 8.
由表 8可知,在航空安全事件数据集上,I_IterE模型的链接预测结果相比于IterE模型均有显著提高,表明I_IterE模型利于航空安全事件知识图谱的补全.针对航空安全事件知识图谱补全效果进行分析,如下所述.
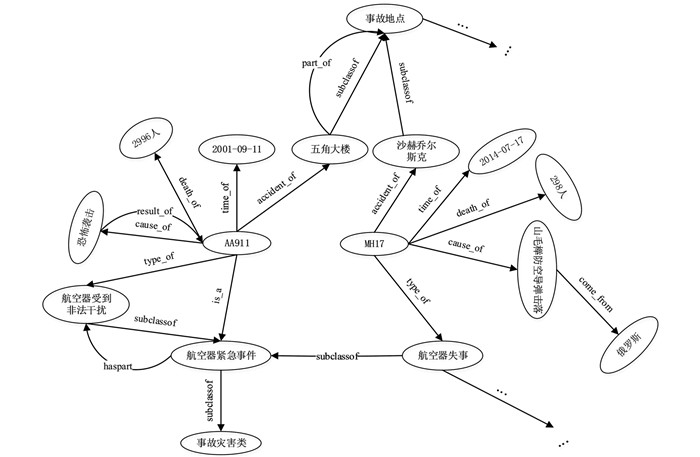
首先,表示学习层需输入航空安全事件知识图谱(图 3).
其次,依据OWL2的7种对象属性表达公理生成可能的公理集,并结合增强后的关系特征与改进的评分机制对公理进行评分(表 9).
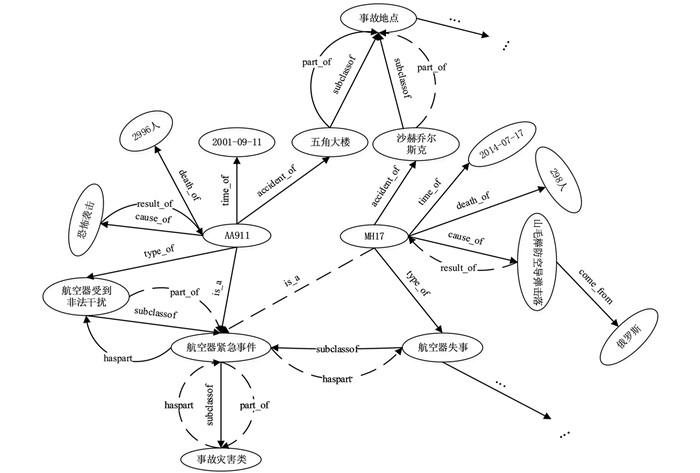
最后,基于得分大于等于0.9的公理推演出新三元组见表 10,加黑的三元组表示新三元组,并将其更新到知识图谱(图 4),虚线箭头表示新添加的两实体间存在的语义关系.
2.1. 实验过程
2.2. 效果分析
-
本研究提出了一种改进的知识图谱补全方法(I_IterE),通过增加模型深度且改进评分机制,有效提升了链接预测的准确率和规则学习的效率,在获得较多高质量规则实现推理的同时,进一步提高了模型的泛化能力.将该方法应用于航空安全事件数据集,较好地解决了航空安全事件知识图谱的补全问题.未来围绕OWL2的数据属性表达公理和类属性表达公理,可以进一步研究知识图谱补全的优化方法.



 下载:
下载: