设E是非空集，对于固定的整数n＞0和所有的x∈E，映射f：E→E的n次迭代被定义为fⁿ(x)=f(f^n-1(x))和f⁰(x)=x.

迭代运算是数学中的重要运算之一，它在许多复杂的问题，如分岔、混沌和分形^[1-3]问题、多项式^[4-8]、拟多项式^[9-10]、线性分式^[11]和有理函数^[12]等问题中有广泛的应用. 在一维的情况下，高次迭代的计算也是一项复杂的工作. 随着C⁰映射迭代理论的发展^[13-14]，人们也逐渐开始研究不连续映射或者集值映射等“坏映射”的迭代和它们的迭代根^[15-18].

通常，人们认为一个“坏映射”可能会通过迭代运算变得更加复杂，但文献[19]表明不连续的自映射通过迭代运算可能变为连续的自映射，并给出了在紧区间上只有一个间断点的分段C⁰自映射的二次迭代连续性的充要条件. 文献[20]进一步研究了在紧区间上只有一个非光滑点的连续自映射二次迭代的光滑性，并给出了它们的二次迭代是C¹光滑映射的充要条件. 文献[20]的工作不是对文献[19]的工作的重复，因为文献[20]所考虑的映射的导数可能不是自映射. 综合文献[19-20]，我们可以判断在紧区间上只有一个间断点的分段C¹自映射四次迭代的C¹光滑性. 但是我们还不能判断：在紧区间上什么不连续的自映射的二次迭代不仅连续而且C¹光滑? 例如，自映射

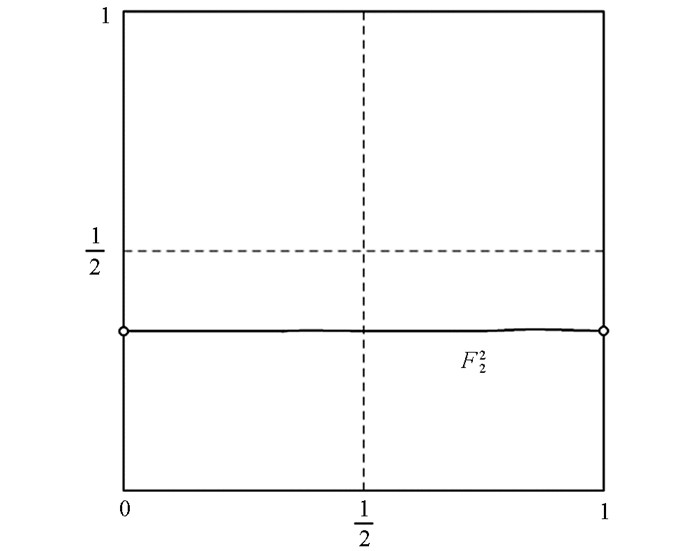
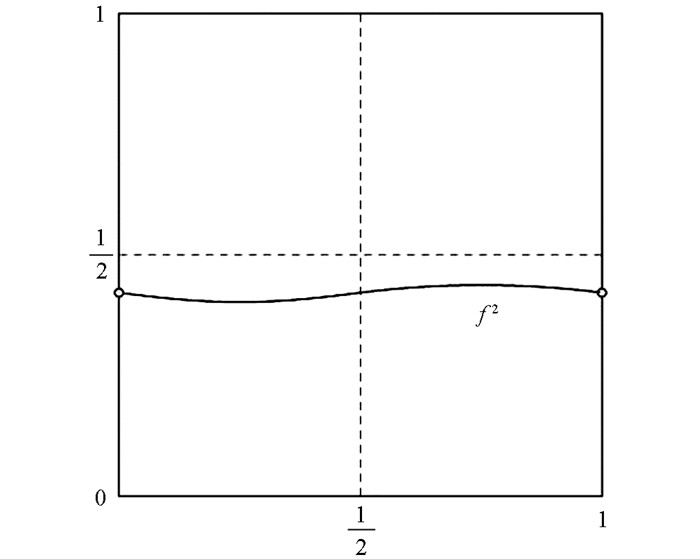
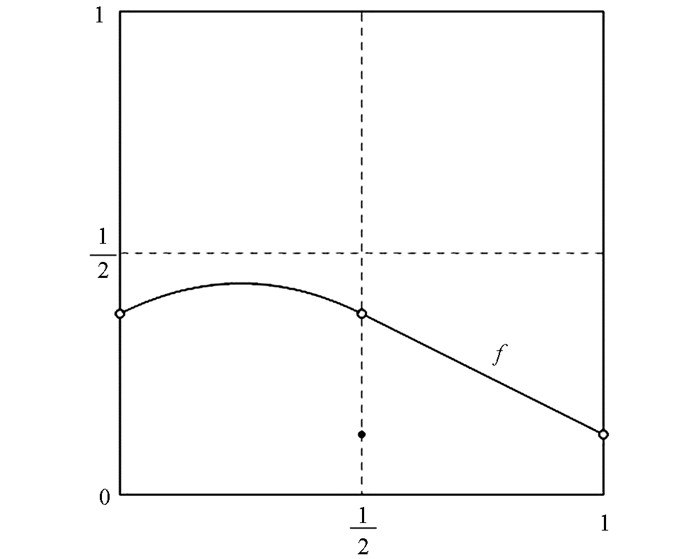
它有一个可去间断点 ${x_0} = \frac{1}{2}$ (图 1)，但它的二次迭代

在(0，1)上是C¹光滑的(图 2).

本文研究在区间I=(0，1)上只有一个可去间断点的所有分段C¹自映射V_r(I，I). 每个f∈V_r(I，I)能被表示为

其中，x₀∈(0，1)是f唯一的可去间断点，f₁和f₂分别在I₁和I₂上是C¹光滑的，c∈(0，1)是一个常数. 为了研究在V_r(I，I)中映射的二次迭代的光滑性，我们需要将V_r(I，I)分成一些子类，即V_r(I，I)=V_rr(I，I)∪V_rj(I，I)∪V_ro(I，I)∪V_r∞(I，I)，其中：

f∈V_rr(I，I)表示f∈V_r(I，I)，且导数f^′有一个可去间断点x₀，也就是$\mathop {\lim }\limits_{x \to x_0^ - } f_1^\prime (x){\rm{ }}$和$\mathop {\lim }\limits_{x \to x_0^ + } f_2^\prime (x)$存在并相等；

f∈V_rj(I，I)表示f∈V_r(I，I)，且导数f^′有一个跳跃间断点x₀，也就是$\mathop {\lim }\limits_{x \to x_0^ - } f_1^\prime (x)$和$\mathop {\lim }\limits_{x \to x_0^ + } f_2^\prime (x)$存在但是不相等；

f∈V_ro(I，I)表示f∈V_r(I，I)，且导数f^′有一个振荡间断点x₀，也就是f₁^′和f₂^′两者都有界，但是$\mathop {\lim }\limits_{x \to x_0^ - } f_1^\prime (x){\rm{ }}$和$\mathop {\lim }\limits_{x \to x_0^ + } f_2^\prime (x)$中至少有一个不存在；

f∈V_r∞(I，I)表示f∈V_r(I，I)，且导数f^′有一个无穷间断点x₀，也就是$\mathop {\lim }\limits_{x \to x_0^ - } f_1^\prime (x) = \infty $，或者$\mathop {\lim }\limits_{x \to x_0^ + } f_2^\prime (x) = \infty $.

本文讨论V_r(I，I)中映射的二次迭代的C¹光滑性. 首先给出了在V_rτ(I，I)中映射的二次迭代是C¹光滑映射的充要条件，其中τ∈{r，j，o}，获得了在V_r∞(I，I)中映射的二次迭代是C¹光滑映射的必要条件. 其次说明了找V_r∞(I，I)中映射的二次迭代是C¹光滑映射的充分条件的困难. 最后用例子展示了在V_r(I，I)中映射的二次迭代是C¹光滑映射的条件.

下面讨论由(1)式定义的f∈V_r(I，I)的二次迭代的光滑性. 记

为了方便，记

我们用D₊f和D_-f分别表示f的右导数和f的左导数.

定理1   假定f∈V_rτ(I，I)由(1)式定义，其中τ∈{r，j，o}，且f有唯一的间断点x₀∈(0，1). 令y₀由(2)式定义. 那么，f²在I上是C¹光滑的当且仅当y₀∈I_i，f(I₁∪I₂)⊆I_i成立(i=1，2)和f∈C_rτ(I，I).

证   首先证明必要性. 假定f²在I上是C¹光滑的，那么f²在I上是连续的. 由文献[19]的定理1知，y₀∈I_i，f(I₁∪I₂)⊆I_i和

其中i=1，2. 在下文中，我们只讨论y₀∈I₁和f(I₁∪I₂)⊆I₁的情况，因为y₀∈I₂和f(I₁∪I₂)⊆I₂情况的讨论与y₀∈I₁和f(I₁∪I₂)⊆I₁情况的讨论是完全类似的. 下证在y₀∈I₁和f(I₁∪I₂)⊆I₁的情况下，有

假设f∈V_rτ(I，I)，其中τ∈{r，j，o}.

情形1   f∈V_rr(I，I). 由(3)式和C_rr(I，I)的定义，我们知道f∈C_rr(I，I).

情形2   f∈V_rj(I，I). 由V_rj(I，I)的定义，我们有

由(4)式得到f²在x₀的左导数和右导数分别为

因为f²在I上是C¹光滑的，所以D_-f²(x₀)=D₊f²(x₀). 注意到y₁≠y₂. 由(5)式和(6)式得到f₁^′(y₀)=0. 再由y₀∈I₁，有

由(3)，(7)式和C_rj(I，I)的定义，我们知道f∈C_rj(I，I).

情形3   f∈V_ro(I，I). 由V_ro(I，I)的定义，有$\mathop {\lim }\limits_{x \to x_0^ - } {f_1}(x) = \mathop {\lim }\limits_{x \to x_0^ + } {f_2}(x) = {y_0}$，且$\mathop {\lim }\limits_{x \to x_0^ - } f_1^\prime (x)$和$\mathop {\lim }\limits_{x \to x_0^ + } f_2^\prime (x)$中至少有一个不存在. 由(4)式得到f²在x₀的左导数和右导数分别为

注意到

因为f²在I上是C¹光滑的，所以f²在x₀的左导数D_-f²(x₀)和右导数D₊f²(x₀)都存在. 因此(7)式成立. 反证法，假设(7)式不成立，我们有f^′(y₀)=f₁^′(y₀)≠0，由(8)式和(9)式得到$\mathop {\lim }\limits_{x \to x_0^ - } f_1^\prime (x) $和$\mathop {\lim }\limits_{x \to x_0^ + } f_2^\prime (x)$都存在. 因为

这与$\mathop {\lim }\limits_{x \to x_0^ - } f_1^\prime (x)$和$\mathop {\lim }\limits_{x \to x_0^ + } f_2^\prime (x)$中至少有一个不存在相矛盾. 因此(7)式成立. 由(3)，(7)式和C_ro(I，I)的定义，我们知道f∈C_ro(I，I). 于是，必要性得证.

其次证明充分性. 我们仅证明y₀∈I₁，f(I₁∪I₂)⊆I₁的情况.

如果f(I₁∪I₂)⊆I₁，则(4)式成立. 因为f₁和f₂分别在I₁和I₂上是C¹光滑的，所以f²在I₁∪I₂上是C¹光滑的. 因为y₀∈I₁，所以f(y₀)=f₁(y₀)，f^′(y₀)=f₁^′(y₀). 由于f∈C_rτ(I，I)，其中τ∈{r，j，o}，所以分3种情况讨论：

当f∈C_rr(I，I)时，由C_rr(I，I)的定义有f(y₀)=f₁(y₀)=Γ(c)和f∈V_rr(I，I). 由文献[19]的定理1知f²在I上是连续的. 因为f∈V_rr(I，I)，则

由(4)式能获得(5)式和(6)式，则D_-f²(x₀)=D₊f²(x₀). 因此，f²在I上是C¹光滑的.

当f∈C_rj(I，I)时，由C_rj(I，I)的定义，我们有f(y₀)=f₁(y₀)=Γ(c)，f∈V_rj(I，I)和f^′(y₀)=f₁^′(y₀)=0. 类似地，我们知道f²在I上是连续的. 因为f∈V_rj(I，I)，则$\mathop {\lim }\limits_{x \to x_0^ - } {f_1}(x) = \mathop {\lim }\limits_{x \to x_0^ + } {f_2}(x) = {y_0}, {\bar y_1} = \mathop {\lim }\limits_{x \to x_0^ - } f_1^\prime (x) \ne {\bar y_2} = \mathop {\lim }\limits_{x \to x_0^ + } f_2^\prime (x)$. 由(4)式能获得(5)式和(6)式，假设f₁^′(y₀)=0，得到D_-f²(x₀)=D₊f²(x₀)=0. 因此，f²在I上是C¹光滑的.

当f∈C_ro(I，I)时，由C_ro(I，I)的定义有f(y₀)=f₁(y₀)=Γ(c)，f∈V_ro(I，I)和f^′(y₀)=f₁^′(y₀)=0. 类似地得到f²在I上是连续的. 因为f∈V_ro(I，I)，则$\mathop {\lim }\limits_{x \to x_0^ - } {f_1}(x) = \mathop {\lim }\limits_{x \to x_0^ + } {f_2}(x) = {y_0}$，且$\mathop {\lim }\limits_{x \to x_0^ - } f_1^\prime (x){\rm{ }}$和$\mathop {\lim }\limits_{x \to x_0^ + } f_2^\prime (x)$中至少有一个不存在，但是f₁^′和f₂^′都有界. 由(4)式能得到(8)式和(9)式，由假设f₁^′(y₀)=0，有

因为f₁^′和f₂^′都有界，结合(8)，(9)式和无穷小量的性质，得到D_-f²(x₀)=D₊f²(x₀)=0.

综上所述，f²在I上是C¹光滑的.

定理2   假定f∈V_r∞(I，I)由(1)式定义，x₀∈(0，1)是f的唯一间断点. 令y₀由(2)式定义. 假设f²在I上是C¹光滑的，则y₀∈I_i，f(I₁∪I₂)⊆I_i(i=1，2)，且f∈C_r∞(I，I).

证   证明方法与定理1中f∈V_ro(I，I)的必要性的证明完全类似.

注1   定理2没有给出f²在I上是C¹光滑映射的充分条件，因为我们不能确定f²在x₀的左导数${D_ - }{f^2}\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to x_0^ - } f_i^\prime \left( {{f_1}(x)} \right)f_1^\prime (x)$或者右导数${D_ + }{f^2}\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to x_0^ + } f_i^\prime \left( {{f_2}(x)} \right)f_2^\prime (x)$的存在性，其中i=1，2. 事实上，如果y₀∈I₁，f(I₁∪I₂)⊆I₁和f∈C_r∞(I，I)，与定理1类似的讨论可得到(8)式和(9)式. 又因为f∈C_r∞(I，I)，则$\mathop {\lim }\limits_{x \to x_0^ - } f_1^\prime \left( {{f_1}(x)} \right) = \mathop {\lim }\limits_{x \to x_0^ + } f_1^\prime \left( {{f_2}(x)} \right) = f_1^\prime \left( {{y_0}} \right) = {f^\prime }\left( {{y_0}} \right) = 0$，且$\mathop {\lim }\limits_{x \to x_0^ - } f_1^\prime (x) = \infty $或者$\mathop {\lim }\limits_{x \to x_0^ + } f_2^\prime (x) = \infty $. 由(8)式和(9)式，我们无法确定D_-f²(x₀)或者D₊f²(x₀)的存在性. 类似地，对另一种情形，我们也无法确定D_-f²(x₀)或者D₊f²(x₀)的存在性.

例1   考虑映射f：(0，1)→(0，1)：

有唯一的可去间断点 ${x_0} = \frac{1}{2}$ (图 1)，因为

其中

则f∈V_rr(I，I). 注意到${I_1} = \left( {0, \frac{1}{2}} \right), {I_2} = \left( {\frac{1}{2}, 1} \right)$. 容易验证$c = \frac{1}{8} \in {I_1}, {y_0} \in {I_1}, f\left( {{I_1} \cup {I_2}} \right) \subseteq {I_1}$，而且f(y₀)=f₁(y₀)=f₁(c)，即f∈C_rr(I，I). 这说明定理1的假设条件满足. 另外，我们能算出f的二次迭代f²在(0，1)上是C¹光滑的(图 2).

例2   考虑映射F₁：(0，1)→(0，1)：

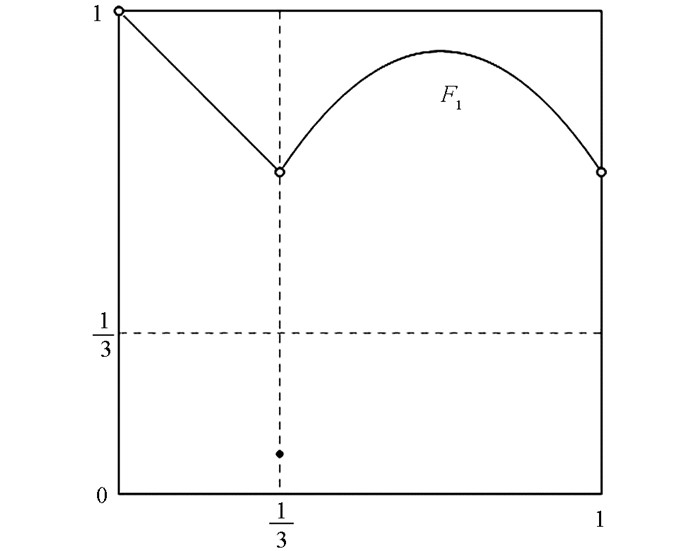
它有唯一的可去间断点${x_0} = \frac{1}{3}$ (图 3)，因为

其中

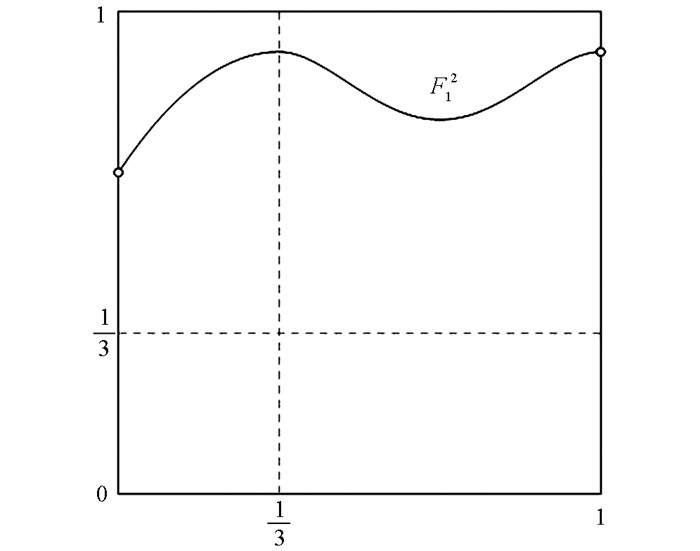
则F₁∈V_rj(I，I). 注意到${I_1} = \left( {0, \frac{1}{3}} \right), {I_2} = \left( {\frac{1}{3}, 1} \right)$. 容易验证$c = \frac{1}{{12}} \in {I_1}, {y_0} \in {I_2}, {F_1}\left( {{I_1} \cup {I_2}} \right) \subseteq {I_2}$，而且F₁(y₀)=f₂(y₀)=f₁(c)和F₁^′(y₀)=f₂^′(y₀)=0，即F₁∈C_rj(I，I). 这说明定理1的假设条件满足. 另外，我们能算出F₁的二次迭代为

它在(0, 1) 上是C¹光滑的(图 4).

例3   考虑映射F₂：(0，1)→(0，1)：

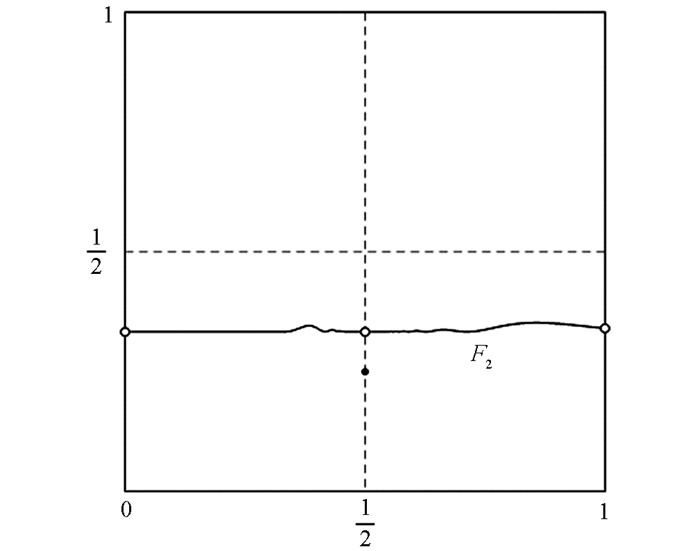
它有唯一的可去间断点${x_0} = \frac{1}{2}$ (图 5)，因为

而且

都不存在，但是f₁^′和f₂^′都有界，其中

则F₂∈V_ro(I，I). 注意到

容易验证$ c = \frac{1}{4} \in {I_1}$，y₀∈I₁，F₂(I₁∪I₂)⊆I₁，而且F₂(y₀)=f₁(y₀)=f₁(c)和F₂^′(y₀)=f₁^′(y₀)=0，即F₂∈C_ro(I，I). 这说明定理1的假设条件满足. 另外，我们能算出F₂的二次迭代为

它在(0，1)上是C¹光滑的(图 6).

注2   如果I=[0, 1]是一个闭区间，我们研究

其中f₊^′(0)=f_-^′(1)=0. 显然，$\hat f \in {V_r}(I, I)$但f∈V_r(I，I).

在这篇文章中，我们仅考虑了(1)式定义的映射唯一的间断点是可去间断点的情形，对(1)式定义的映射唯一间断点是跳跃或者振荡间断点的情形，我们将在后续文章中加以研究.