高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

丘陵地区地表温度垂直递减率的变化特征——以重庆市为例

, 

上一篇

下一篇

廖代强, 柴闯闯. 丘陵地区地表温度垂直递减率的变化特征——以重庆市为例[J]. 西南大学学报（自然科学版）, 2021, 43(9): 124-130. doi: 10.13718/j.cnki.xdzk.2021.09.014
引用本文: 廖代强, 柴闯闯. 丘陵地区地表温度垂直递减率的变化特征——以重庆市为例[J]. 西南大学学报（自然科学版）, 2021, 43(9): 124-130. doi: 10.13718/j.cnki.xdzk.2021.09.014
shu
LIAO Daiqiang, CHAI Chuangchuang. Fluctuation in Vertical Decline Rate of Surface Temperature in Hilly Areas——A Case Study of Chongqing[J]. Journal of Southwest University Natural Science Edition, 2021, 43(9): 124-130. doi: 10.13718/j.cnki.xdzk.2021.09.014
Citation: LIAO Daiqiang, CHAI Chuangchuang. Fluctuation in Vertical Decline Rate of Surface Temperature in Hilly Areas——A Case Study of Chongqing[J]. Journal of Southwest University Natural Science Edition, 2021, 43(9): 124-130. doi: 10.13718/j.cnki.xdzk.2021.09.014
shu

丘陵地区地表温度垂直递减率的变化特征——以重庆市为例

  • 1.

    重庆市气候中心，重庆 401147

  • 2.

    重庆舍特气象应用研究所，重庆 401147

  • 基金项目: 国家重点研发计划项目(2017YFC1502402)；重庆市气象局业务技术攻关项目(YWGGMS-201803，YWJSGG-202015)
详细信息
    作者简介:

    廖代强，硕士，教授级高级工程师，主要从事气候应用服务研究 .

  • 中图分类号: P423.1

Fluctuation in Vertical Decline Rate of Surface Temperature in Hilly Areas——A Case Study of Chongqing

  • 1.

    Chongqing Climate Center, Chongqing 401147, China

  • 2.

    Chongqing Institute of Applied Meteorology, Chongqing 401147, China

  • 摘要: 基于重庆市2008-2019年34个国家气象观测站和重庆市所有1 802个区域自动站的逐小时地表温度资料，通过线性拟合法分析丘陵地区的地表温度垂直递减率. 结果表明：年、月、坡向和水体边温度垂直递减率的日变化趋势基本一致，大致可划分为3个阶段：平稳期，上升期，下降期；季节变化是夏季变化幅度最大，冬季最小；月变化幅度最大是7月；东坡大于北坡和西坡，南坡最小；地表温度递减率日内变化起伏较大，最大值均出现在19时，最小值出现在10时或11时.
    Abstract: Based on thehourly surface temperature data from 34 national meteorological observation stations of Chinaand 1 802 regional automatic stations in Chongqing from 2008 to 2019, this paper analyzes the vertical decline rate of surface temperature in hilly areas with the linear fitting method. The results are as follows. The diurnal variation trend of year, month, slope direction and the vertical decline rate of water side temperature is basically the same, which can be roughly divided into three stages: astationary phase, anascending phase and a descending phase. The seasonal variation is the largest in summer and the smallest in winter. The monthly change is the largest in July, being larger in the eastern slope than in the northern slope and the western slope, and the smallest in the southern slope. The diurnal fluctuation of the land surface temperature decline rate is great, with the maximum value appearing at 19o'clock and the minimum at 10 or 11 o'clock.
  • 加载中

  • 图 1  重庆市2018年地面气象观测站点分布

    下载: 全尺寸图片 幻灯片

    图 2  年内地表温度递减率月变化分布

    下载: 全尺寸图片 幻灯片

    图 3  年内地表温度递减率日变化分布

    下载: 全尺寸图片 幻灯片

    图 4  年内季节变化

    下载: 全尺寸图片 幻灯片

    图 5  不同季节地表温度递减率日内分布

    下载: 全尺寸图片 幻灯片

    图 6  各月份地表温度递减率日内分布

    下载: 全尺寸图片 幻灯片

    图 7  不同坡向和水体边地表温度递减率日内分布

    下载: 全尺寸图片 幻灯片

    表 1  不同坡向和水体的样本数

    属性 样本数量 属性 样本数量
    东坡 465 北坡 201
    南坡 635 水体 65
    西坡 436
    下载: 导出CSV

    表 2  不同属性和时间尺度的温度递减率公式

    时间和属性 方程 R R2
    年 T=-0.005 8h+19.923 0.915* 0.837
    春季 T=-0.005 9h+19.969 0.917* 0.841
    夏季 T=-0.005 9h+28.801 0.922* 0.849
    秋季 T=-0.005 4h+19.88 0.927* 0.859
    冬季 T=-0.005 8h+10.092 0.916* 0.839
    东坡 T=-0.005 9h+19.968 0.931* 0.867
    南坡 T=-0.005 7h+19.924 0.925* 0.856
    西坡 T=-0.005 5h+19.854 0.928* 0.861
    北坡 T=-0.005 6h+19.851 0.914* 0.835
    水体边 T=-0.005 4h+20.423 0.613* 0.375
    1月 T=-0.005 6h+9.2327 0.906* 0.820
    2月 T=-0.005 9h+10.751 0.910* 0.828
    3月 T=-0.006 2h+16.129 0.898* 0.807
    4月 T=-0.005 8h+20.593 0.911* 0.830
    5月 T=-0.005 5h+23.154 0.928* 0.861
    6月 T=-0.005 4h+26.383 0.935* 0.875
    7月 T=-0.006 1h+30.298 0.900* 0.811
    8月 T=-0.006 3h+29.725 0.909* 0.826
    9月 T=-0.005 3h+24.529 0.917* 0.841
    10月 T=-0.005 4h+20.039 0.924* 0.853
    11月 T=-0.005 6h+15.049 0.916* 0.839
    12月 T=-0.005 8h+10.285 0.916* 0.839
    注：表示p=0.01水平差异具有统计学意义.
    下载: 导出CSV
  • [1] doi: http://www.researchgate.net/profile/Harry_Kambezidis/publication/304252069_Estimation_of_the_monthly_and_annual_mean_maximum_and_mean_minimum_air_temperature_values_in_Greece/links/576aadf708aefcf135bd3944/Estimation-of-the-monthly-and-annual-mean-maximum-and-mean-minimum-air-temperature-values-in-Greece.pdf GOUVAS M A, SAKELLARIOU N K, KAMBEZIDIS H D. Estimation of the Monthly and Annual Mean Maximum and Mean Minimum Air Temperature Values in Greece[J]. Meteorology and Atmospheric Physics, 2011, 110(3/4): 143-149.
    [2] GARDNER A S, SHARP M J, KOERNER R M, et al. Near-Surface Temperature Lapse Rates over Arctic Glaciers and Their Implications for Temperature Downscaling[J]. Journal of Climate, 2009, 22(16): 4281-4298. doi: 10.1175/2009JCLI2845.1
    [3] STONE P H, CARLSON J H. Atmospheric Lapse Rate Regimes and Their Parameterization[J]. Journal of the Atmospheric Sciences, 1979, 36(3): 415-423. doi: 10.1175/1520-0469(1979)036<0415:ALRRAT>2.0.CO;2
    [4] ROLLAND C. Spatial and Seasonal Variations of Air Temperature Lapse Rates in Alpine Regions[J]. Journal of Climate, 2003, 16(7): 1032-1046. doi: 10.1175/1520-0442(2003)016<1032:SASVOA>2.0.CO;2
    [5] doi: http://www.onacademic.com/detail/journal_1000034476303310_3634.html PEPIN N. Lapse Rate Changes in Northern England[J]. Theoretical and Applied Climatology, 2001, 68(1/2): 1-16.
    [6] PEPIN N. Twentieth-Century Change in the Climate Record for the Front Range, Colorado, USA[J]. Arctic, Antarctic, and Alpine Research, 2000, 32(2): 135-146. doi: 10.1080/15230430.2000.12003349
    [7] 刘伟刚, 张东启, 柳景峰, 等. 喜马拉雅山中段地区气温直减率变化特征[J]. 干旱气象, 2013, 31(2): 240-245. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-GSQX201302003.htm
    [8] 方精云. 我国气温直减率分布规律的研究[J]. 科学通报, 1992, 37(9): 817-820. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-KXTB199209013.htm
    [9] 郑成洋, 方精云. 福建黄岗山东南坡气温的垂直变化[J]. 气象学报, 2004, 62(2): 251-255. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-QXXB200402012.htm
    [10] 田杰, 王庆伟, 于大炮, 等. 长白山北坡气温的垂直变化[J]. 干旱区资源与环境, 2013, 27(4): 65-69. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-GHZH201304010.htm
    [11] 林长伟, 常晓丽. 山区地表温度垂直递减率的时空分布特征——以祁连山为例[J]. 地球科学前沿(汉斯), 2018, 8(3): 691-698.
    [12] 江志红, 祝亚鹏, 马红云, 等. 同化自动站资料建立三峡地区2014年1月高分辨率温度场的模拟研究[J]. 大气科学学报, 2018, 41(3): 289-297. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-NJQX201803001.htm
    [13] 毛文书, 彭骏, 周强, 等. 基于Barnes滤波原理的降水场客观分析及尺度分离[J]. 成都信息工程学院学报, 2008, 23(6): 668-672. doi: 10.3969/j.issn.1671-1742.2008.06.016
    [14] 刘劲宏, 姚宜斌, 桑吉章. 温度递减率对加权平均温度的影响[J]. 大地测量与地球动力学, 2019, 39(6): 639-642. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-DKXB201906017.htm
    [15] 王浩. 陆地水体对气候影响的数值研究[J]. 海洋与湖沼, 1991, 22(5): 467-473. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-HYFZ199105010.htm
    [16] 李书严, 轩春怡, 李伟, 等. 城市中水体的微气候效应研究[J]. 大气科学, 2008, 32(3): 552-560. doi: 10.3878/j.issn.1006-9895.2008.03.12
  • 加载中
图( 7) 表( 2)
计量
  • 文章访问数:  3776
  • HTML全文浏览数:  3776
  • PDF下载数:  537
  • 施引文献:  0
出版历程
  • 收稿日期:  2020-07-17
  • 刊出日期:  2021-09-20

丘陵地区地表温度垂直递减率的变化特征——以重庆市为例

    作者简介: 廖代强，硕士，教授级高级工程师，主要从事气候应用服务研究
  • 1. 重庆市气候中心，重庆 401147
  • 2. 重庆舍特气象应用研究所，重庆 401147
  • 收稿日期:  2020-07-17
基金项目:  国家重点研发计划项目(2017YFC1502402)；重庆市气象局业务技术攻关项目(YWGGMS-201803，YWJSGG-202015)

摘要: 基于重庆市2008-2019年34个国家气象观测站和重庆市所有1 802个区域自动站的逐小时地表温度资料，通过线性拟合法分析丘陵地区的地表温度垂直递减率. 结果表明：年、月、坡向和水体边温度垂直递减率的日变化趋势基本一致，大致可划分为3个阶段：平稳期，上升期，下降期；季节变化是夏季变化幅度最大，冬季最小；月变化幅度最大是7月；东坡大于北坡和西坡，南坡最小；地表温度递减率日内变化起伏较大，最大值均出现在19时，最小值出现在10时或11时.

English Abstract

    全文HTML

  • 山地气候的垂直变化是一个经典的地理学和气候学问题，对生态学研究也十分重要，是区域生态系统、城市热岛、天气预报、水温循环和环境演化等分析研究和模型模拟的重要变量和基础资料. 一般认为，在对流层内自由大气的温度递减率为0.065 ℃/km. 但在不同的环境条件下，温度递减率往往有所差异. 影响温度递减率变化的要素复杂多样[1-3]，包括下垫面条件、海拔、空气湿度、云量、能量平衡组成等，其中空气湿度扮演着重要的角色[4]. 而且自由大气与地面递减率不同. 在一个温度较高的地方，地表温度递减率可能会发生变化[5].

    目前，国内外学者非常重视山区气候变化，也对温度垂直递减率进行过研究，Pepin[6]对美国落基山脉地表递减率的系统变化进行了研究；刘伟刚等[7]研究了喜马拉雅山中段地区气温直减率变化特征；方精云[8]的研究显示我国地面温度垂直递减率在0.025~0.063 ℃/km范围内波动；郑成洋等[9]对福建黄岗山东南坡温度的垂直变化分析得出年均温的递减率为0.043 ℃/km；田杰等[10]研究了长白山北坡温度的垂直变化. 这些方法虽然能反映山区气候的一般趋势，取得一定的研究成果，但山地气候因复杂的地理、地形等条件具有明显的区域小气候特征，因此传统意义上的温度递减率结果并不适用于山地气候区[11]，特别是丘陵地区，由于受气象台(站)条件监测的限制，温度的连续观测一般难以实现，从而很难准确地获得连续、多年的温度变化信息.

    本文利用重庆市2008-2019年2 055个(经过质量控制后，剩余1 802个站点)加密的区域自动站的资料，弥补了以前观测资料的不足且避免了遥感资料的误差，对重庆温度垂直递减率的时空分布特征做了较详细的分析研究，为山地丘陵地区水文、农业、林业、旅游和生态等合理地、科学地开发及可持续发展提供数据参考和科学依据.

1.   资料与方法

    1.1.   研究区域

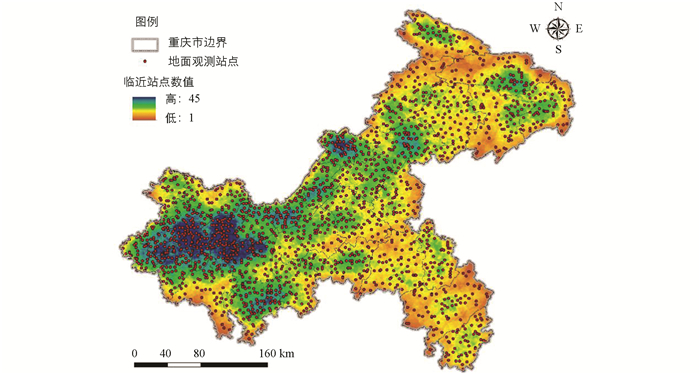
  • 研究区域：重庆市地处中国内陆西南部，地貌以丘陵、山地为主，其山地丘陵占76%，东邻湖北、湖南，南靠贵州，西接四川，北连陕西. 地跨东经105°11′-110°11′、北纬28°10′-32°13′之间. 研究数据选取34个国家气象观测站点和重庆市所有2 055个(经过质量控制后，剩余1 802个站点)区域自动站资料，具体区域和站点情况如图 1所示.

    • 1.2.   数据检验与处理

  • 由于自动站资料存在缺测或观测错误，因此必须对其进行质量控制. 参考江志红等[12]的研究成果对数据进行温度极值检验、时间连续性检验、空间连续性检验.

    • 1.2.1.   温度极值检验

  • 首先直接剔除数据已标识为缺测的数据，然后通过判断要素数据是否位于特定阈值范围内，从而进一步对可疑数据进行筛除. 根据重庆本地的气候状况，日平均温度的阈值设置为-20~40 ℃，超过该阈值的数据便判断为缺省值.

    • 1.2.2.   时间连续性检验

  • 温度变化与时间存在较为显著的相关性，邻近日期的要素值应当是连续均匀变化的，时间连续性检验就是将出现过度变化或变化过小的气象要素值判断为可疑数据进行剔除处理. 本研究中以温度连续4 d的平均变率为基础，若某一站点4 d的平均变率超过15 ℃或小于0.5 ℃，则设置为缺省值.

    • 1.2.3.   空间连续性检验

  • 同一区域范围内的站点观测数据可表现出相似的空间分布特征，若某个测站的要素值与邻近站差异较大，则可判断此站点的要素为可疑数据. 将距离质控站点周围一定范围内的所有站点作为样本，根据Barnes客观分析法插值[13]到质控站点位置，然后判断站点原数据与插值数据间的残差，若超过特定阈值则该要素值判断为缺测. 相关计算方程为

    式(1)中x'为残差值，xj和xi分别为质控站点原始值和周围站点值，ωi为周围站点权重，r为周围站点到质控站点的距离，R为影响半径.

    由于进行空间连续性检查需要使用周边站点进行插值，若某个还未进行质控的可疑站点也参与到插值中势必会对结果造成影响，因此研究中采用了二次迭代方案，即首先对所有站点进行1次空间连续性检验，然后在第2次检验中只使用通过了第1次检验的站点进行插值. 若某个站点在第2次空间连续性检验中依然被判断为可疑值，便剔除；反之，则保留. 进行质控时，影响半径设为20 km，温度的最大残差值为6 ℃. 利用经过质量控制后的资料，剩余1 802个站点作为本文的基础数据样本(表 1).

    • 1.3.   研究方法

  • 温度的垂直变化与高度有着较吻合的线性关系，这个线性关系的系数就是温度垂直递减率，简称温度递减率. 由于温度受纬度、下垫面、气流等因素的影响，温度递减率随地点、季节、昼夜的不同而变化. 本文为了准确分析丘陵地区温度垂直变化特征，建立不同海拔的温度(T)和海拔(H)之间的一元回归方程，方程的斜率即是温度递减率(δ). 计算公式为：

    式(3)中，Ts为地表温度，单位为℃；δ为温度递减率，单位为℃/km.

    将温度递减率作为待拟合参数，采用最小二乘法原理对观测的温度垂直廓线进行线性拟合，即可求得对应观测时刻的温度递减率[14].

2.   结果分析

    2.1.   年、季、月的温度递减率公式

  • 利用重庆市2008-2019年1 802个自动气象观测站的逐小时温度资料，根据以上温度递减率的计算公式，采用最小二乘法拟合得到重庆市不同坡向、水体边(与长江和嘉陵江距离1 km以内[15-16)、年、季、月的温度递减率公式(表 2).

    • 2.2.   年内月、日分布特征

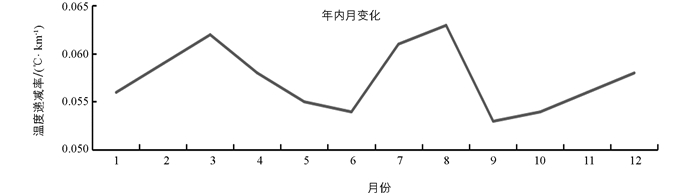
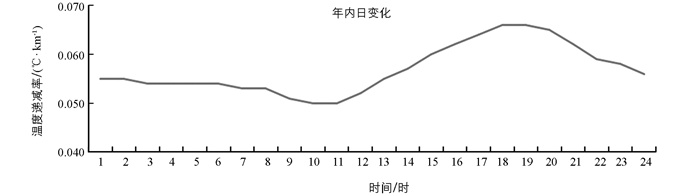
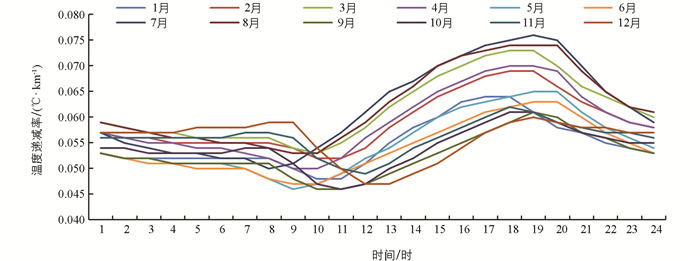
  • 为了探讨地表温度垂直递减率在各月的变化特征，根据选取的全市自动站资料分析得到年内不同月份和日内地表温度垂直递减率变化特征折线图，分别见图 2、图 3.总体来看，各月的地表温度递减率变化幅度不大，其中最大值出现在8月(0.063 ℃/km)，最小值出现在9月(0.053 ℃/km)，相差仅0.01 ℃/km. 相比年月变化而言，年内日变化幅度相对较大，为0.016 ℃/km；变化趋势分为3个阶段，1时-10时为变化不大的平稳期，11时-19时为上升期，10时-24时为下降期. 地表温度递减率的日变化是地表大气湍流交换过程的具体体现[7]，在19时左右，大气湍流运动最剧烈，地表温度递减率最高；而在11时左右，大气层结相对稳定，常有逆温发生，这时地表温度递减率最低.

    • 2.3.   不同季节分布特征

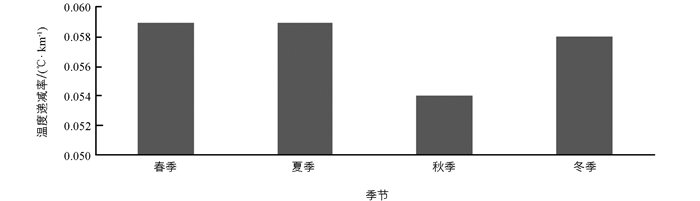
  • 为了解1年内4个季节中的变化情况，按照春季(3-5月)、夏季(6-8月)、秋季(9-11月)和冬季(12-翌年2月)分别统计地表温度垂直递减率在不同季节的分布特征. 从图 4可以明显看出，地表温度垂直递减率在不同季节波动幅度存在差异. 秋季的地表温度垂直递减率为4个季节中最低(0.054 ℃/km)，其次是冬季、春季和夏季，其中夏季最高(0.059 ℃/km).

    • 2.4.   不同季节日内分布特征

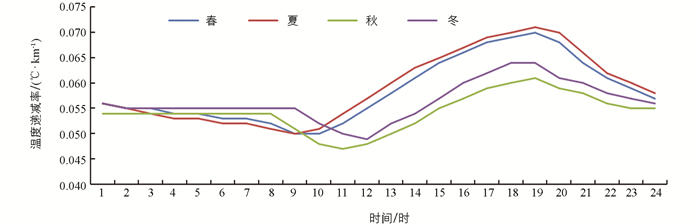
  • 为分析不同季节地表温度垂直递减率在日内的变化特征，根据计算结果绘制不同季节日内地表温度垂直递减率变化特征折线图(图 5). 总体来说，4个季节的平均地表温度垂直递减率在日内(1时-24时)变化形式基本一致，大致可划分为3个阶段：平稳期(1时-10时)，上升期(11时-19时)，下降期(20时-24时)，变化过程均呈“勺子”形；其中夏季变化幅度最大，冬季最小. 从平均尺度上看，丘陵地区的地表温度垂直递减率从大到小依次为夏季和春季、冬季、秋季，其中春季和夏季平均变化情况基本相同；各个季节的地表温度垂直递减率日变化特征差异较大，最大值出现在夏季19时(0.071 ℃/km)，最小值是秋季的11时(0.047 ℃/km)，差值达到0.024 ℃/km.

    • 2.5.   不同月份日内分布特征

  • 图 6是各月份地表温度递减率在日内的起伏情况，与图 3、图 5的基本趋势一致，从1时开始至9时，基本保持不变，然后先上升后下降. 最大值均出现在下午(19时)，最小值出现在上午(10时和11时)，其中7月的变化幅度最大，11月、12月幅度最小. 由此可知，丘陵地区地表月份温度垂直递减率的日内变化与季节、年的日变化相似. 其中7月份(19时)的差值最大，高达0.076 ℃/km，最小值是10月(12时)，仅为0.046 ℃/km.

    • 2.6.   不同坡向和水体边日内分布特征

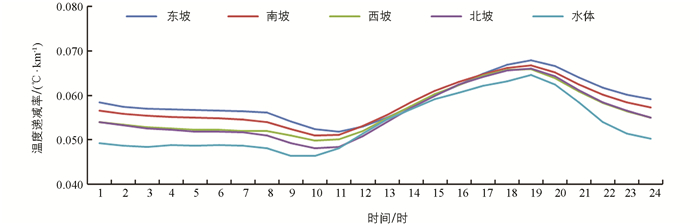
  • 图 7是不同坡向和水体边日内地表温度递减率的分布特征，与图 3、图 5和图 6的基本趋势一致.

    从1时开始至9时，基本保持不变，然后先上升后下降. 最大值均出现在下午(19时)，最小值出现在上午(10时和11时). 其中东坡是所有坡向中地表温度递减率最大的，其次是南坡，北坡和西坡最小且变化特征基本一致；水体边的温度递减率由于水的热容量大，导致其温度递减率最小.

3.   结语

    3.1.   主要结论

  • 本文利用重庆市2008-2019年34个国家气象观测站和1 802个区域自动站的逐小时地表温度资料，分析得到丘陵地区(重庆)地表温度递减率的时空分布特征. 主要结论如下：

    1) 重庆市平均温度随着海拔梯度升高呈明显的下降趋势，年平均温度递减率为0.058 ℃/km. 一年之中，8月份温度递减率最大，9月份最小.

    2) 重庆市年、季、月地表温度垂直递减率的变化趋势基本一致，大致可划分为3个阶段：平稳期、上升期，下降期；不同坡向中，东坡在所有坡向中地表温度递减率最大，水体边的温度递减率最小.

    3) 年、月、坡向和水体边的地表温度递减率在日内的变化情况都是1时-9时基本保持不变，然后先上升后下降. 最大值出现在下午(19时)，最小值出现在上午(10时和11时).

    • 3.2.   存在的不足

  • 本文主要研究丘陵地区(重庆市)地表温度垂直递减率的时空分布，其中空气湿度、大气稳定度对地表温度递减率的影响明显. 由于地形、下垫面条件、降水等均可能对温度递减率产生影响，因此未来还需要做进一步探讨.

参考文献 (16)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回