高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

双圈图的邻和可区别边染色

,  ,  , 

上一篇

下一篇

谭钧铭, 强会英, 刘欢, 等. 双圈图的邻和可区别边染色[J]. 西南大学学报（自然科学版）, 2022, 44(6): 80-87. doi: 10.13718/j.cnki.xdzk.2022.06.009
引用本文: 谭钧铭, 强会英, 刘欢, 等. 双圈图的邻和可区别边染色[J]. 西南大学学报（自然科学版）, 2022, 44(6): 80-87. doi: 10.13718/j.cnki.xdzk.2022.06.009
shu
TAN Junming, QIANG Huiying, LIU Huan, et al. Neighbor Sum Distinguishing Edge Coloring of Bicyclic Graphs[J]. Journal of Southwest University Natural Science Edition, 2022, 44(6): 80-87. doi: 10.13718/j.cnki.xdzk.2022.06.009
Citation: TAN Junming, QIANG Huiying, LIU Huan, et al. Neighbor Sum Distinguishing Edge Coloring of Bicyclic Graphs[J]. Journal of Southwest University Natural Science Edition, 2022, 44(6): 80-87. doi: 10.13718/j.cnki.xdzk.2022.06.009
shu

双圈图的邻和可区别边染色

  • 1.

    兰州交通大学 数理学院, 兰州 730070

  • 2.

    兰州理工大学 机电工程学院, 兰州 730050

  • 基金项目: 国家自然科学基金项目(61962035, 11961041)
详细信息
    作者简介:

    谭钧铭，硕士研究生，主要从事图论及其应用的研究 .

  • 中图分类号: O157.5

Neighbor Sum Distinguishing Edge Coloring of Bicyclic Graphs

  • 1.

    School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou 730070, China

  • 2.

    School of Mechanical and Electrical Engineering, Lanzhou University of Technology, Lanzhou 730050, China

  • 摘要: 设G是阶数不小于3的简单连通图. u，v是图G的一个k-正常边染色的任意相邻的两个顶点，如果点u所有关联边的颜色加和与点v所有关联边的颜色加和不相等，则称该染色是邻和可区别的. 对G进行邻和可区别边染色所需要的最少的颜色数k称为G的邻和可区别边色数. 根据双圈图的结构特点，对双圈图的有根树的树高进行分类，运用结构分析法、反证法、构造染色法，以及组合零点定理等方法，研究了双圈图的邻和可区别边染色问题，得到了双圈图的邻和可区别边色数.
    Abstract: Let G be a simple connected graph with order not less than 3. A k-proper edge coloring of G is called neighbor sum distinguishing if for any two adjacent vertices u, v, the sum of colors taken on the edges incident to u is different from the sum of colors taken on the edges incident to v. The smallest k required for a neighbor sum distinguishing edge coloring of G is called the neighbor sum distinguishing edge chromatic number. According to the structures and characteristics of bicyclic graphs, the tree height of the rooted trees of bicyclic graphs was classified. The neighbor sum distinguishing edge colorings of bicyclic graphs were studied by using the methods of structural analysis, contradiction, constructing the colorings, together with Combinatorial Nullstellensatz. Their neighbor sum distinguishing edge chromatic numbers were obtained.
  • 加载中

  • 图 1  无悬挂点的双圈图

    下载: 全尺寸图片 幻灯片

    图 2  满足情形1.2与情形1.3(2)的双圈图的基本结构

    下载: 全尺寸图片 幻灯片

    表 1  H1的邻和可区别边染色

    r，s，t P1 P2 P3
    r，s，t≡0(mod 3) $(123)^{\frac{r}{3}}$ $(231)^{\frac{s}{3}}$ $(312)^{\frac{t}{3}}$
    r，s，t≡1(mod 3) $(231)^{\frac{r-1}{3}} 2$ $(312)^{\frac{s-1}{3}} 3$ $(123)^{\frac{t-1}{3}} 1$
    r，s，t≡2(mod 3) $(231)^{\frac{r-2}{3}} 23$ $(312)^{\frac{s-2}{3}} 31$ $(123)^{\frac{t-2}{3}} 12$
    r，s≡0(mod 3)，t≡1(mod 3) $(213)^{\frac{r}{3}}$ $(312)^{\frac{s}{3}}$ $(123)^{\frac{t-1}{3}} 1$
    r，s≡0(mod 3)，t≡2(mod 3) $(213)^{\frac{r}{3}}$ $(321)^{\frac{s}{3}}$ $(123)^{\frac{t-2}{3}} 12$
    r，s≡1(mod 3)，t≡0(mod 3) $(132)^{\frac{r-1}{3}} 1$ $(231)^{\frac{s-1}{3}} 4$ $(312)^{\frac{t}{3}}$
    r，s≡1(mod 3)，t≡2(mod 3) $(231)^{\frac{r-1}{3}} 2$ $(312)^{\frac{s-1}{3}} 3$ $(123)^{\frac{t-2}{3}} 14$
    r，s≡2(mod 3)，t≡0(mod 3) $(123)^{\frac{r-2}{3}} 12$ $(231)^{\frac{s-2}{3}} 23$ $(321)^{\frac{t}{3}}$
    r，s≡2(mod 3)，t≡1(mod 3) $(231)^{\frac{r-2}{3}} 23$ $(321)^{\frac{s-2}{3}} 32$ $(123)^{\frac{t-1}{3}} 1$
    r≡0(mod 3)，s≡1(mod 3)，t≡2(mod 3) $(123)^{\frac{r}{3}}$ $(231)^{\frac{s-1}{3}} 2$ $(312)^{\frac{t-2}{3}} 31$
    下载: 导出CSV
  • [1] FLANDRIN E, MARCZYK A, PRZYBYLO J, et al. Neighbor Sum Distinguishing Index[J]. Graphs and Combinatorics, 2013, 29(5): 1329-1336. doi: 10.1007/s00373-012-1191-x
    [2] CHEN X E, LIU S Y. Adjacent Vertex Distinguishing Proper Edge Colorings of Bicyclic Graphs[J]. IAENG International Journal of Applied Mathematics, 2018, 48(4): 401-411.
    [3] 潘文华, 徐常青. 无K4-图子式的图的邻和可区别边染色[J]. 数学进展, 2017, 46(6): 839-847. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-SXJZ201706004.htm
    [4] 杨笑蕊, 强会英, 李雨虹. 两类冠图的邻和可区别全染色[J]. 兰州交通大学学报, 2019, 38(5): 114-117. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-LZTX201905017.htm
    [5] 朱海洋, 王淑玲, 刘嫚, 等. 平面图的单射染色[J]. 西南师范大学学报(自然科学版), 2017, 42(4): 7-13. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-XNZK201704002.htm
    [6] 王文杰, 黄丽娜, 李沐春. T-型六角系统的点可区别边染色[J]. 西南大学学报(自然科学版), 2018, 40(10): 77-82. doi: http://xbgjxt.swu.edu.cn/article/doi/10.13718/j.cnki.xdzk.2018.10.013
    [7] 谭钧铭, 强会英, 王洪申. 单圈图的邻和可区别边染色[J]. 山东大学学报(理学版), 2022, 57(2): 78-83, 91. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-SDDX202202013.htm
    [8] 霍京京. 图的邻点及邻和可区别染色[D]. 苏州: 苏州大学, 2017.
    [9] 陈祥恩, 张爽, 李泽鹏. K2, 4, p的点可区别IE-全染色[J]. 电子与信息学报, 2020, 42(12): 2999-3004. doi: 10.11999/JEIT190829
    [10] 林育青. 一类图的邻点可区别全染色[J]. 数学的实践与认识, 2020, 50(20): 263-271. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-SSJS202020031.htm
    [11] 姚京京. 图的邻和可区别染色[D]. 天津: 河北工业大学, 2015.
    [12] 谭钧铭, 强会英, 姚丽. 路和圈的广义Mycielski图的邻和可区别全染色[J]. 淮阴师范学院学报(自然科学版), 2021, 20(1): 1-5. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-HYSK202101001.htm
    [13] 李红杰. 简单图的邻和可区别边染色[D]. 济南: 山东大学, 2016.
    [14] 尚华辉, 闫晓芳, 苗连英. 关于双圈图的动态色数[J]. 太原理工大学学报, 2018, 49(4): 642-644. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-TYGY201804021.htm
    [15] 田双亮, 杨环, 杨青, 等. 路的联的邻和可区别边染色[J]. 山东大学学报(理学版), 2020, 55(9): 29-35. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-SDDX202009004.htm
    [16] DING L H, WANG G H, YAN G Y. Neighbor Sum Distinguishing Total Colorings Via the Combinatorial Nullstellensatz[J]. Science China Mathematics, 2014, 57(9): 1875-1882. doi: 10.1007/s11425-014-4796-0
  • 加载中
图( 2) 表( 1)
计量
  • 文章访问数:  615
  • HTML全文浏览数:  615
  • PDF下载数:  242
  • 施引文献:  0
出版历程
  • 收稿日期:  2021-06-30
  • 刊出日期:  2022-06-20

双圈图的邻和可区别边染色

    作者简介: 谭钧铭，硕士研究生，主要从事图论及其应用的研究
  • 1. 兰州交通大学 数理学院, 兰州 730070
  • 2. 兰州理工大学 机电工程学院, 兰州 730050
  • 收稿日期:  2021-06-30
基金项目:  国家自然科学基金项目(61962035, 11961041)

摘要: 设G是阶数不小于3的简单连通图. u，v是图G的一个k-正常边染色的任意相邻的两个顶点，如果点u所有关联边的颜色加和与点v所有关联边的颜色加和不相等，则称该染色是邻和可区别的. 对G进行邻和可区别边染色所需要的最少的颜色数k称为G的邻和可区别边色数. 根据双圈图的结构特点，对双圈图的有根树的树高进行分类，运用结构分析法、反证法、构造染色法，以及组合零点定理等方法，研究了双圈图的邻和可区别边染色问题，得到了双圈图的邻和可区别边色数.

English Abstract

    全文HTML

  • 开放科学(资源服务)标志码(OSID):

  • 图的染色问题是图论主要研究内容之一. 文献[1]首次提出了图的邻和可区别染色的概念，给出了猜想：对于至少含3个点的连通图G，若G≠C5，有χ'Σ(G)≤Δ(G)+2，并得到了路、圈、完全图等图的邻和可区别边色数. 文献[2]研究了双圈图的邻点可区别边染色. 更多的染色结论，可参见文献[3-8]. 本文研究了双圈图的邻和可区别边染色，得到了双圈图的邻和可区别边色数.

    图G表示一个双圈图，图上的树的高度称为双圈图的有根树的高度. 树上最长路的长度，称为有根树的高. V(G)，E(G)，Δ(G)分别是图G的点集合、边集合、最大度. dG(v)表示在图G中点v的度，Sφ(v)表示在φ下所有与点v相关联的边所染颜色构成的色集合，[k]表示{1，2，…，k}组成的色集合. GΔ表示图G的全体最大度顶点在图G中的导出子图. 文中未加说明的符号可参见文献[9-12].

1.   预备知识

  • 定义1[13]  设φ：E(G)→[k]是阶数至少为3的简单图G的一个k-正常边染色，fφ(v)表示所有与点v相关联的边所染颜色的加和. 如果对∀uv∈E(G)，都有fφ(u)≠fφ(v)，则称φ是图G的一个k-邻和可区别边染色，简记为k-NSDPEC. χ'Σ(G)=min{k|G有k-NSDPEC}.

    定义2[14]  边数等于顶点数加1的简单连通图叫做双圈图.

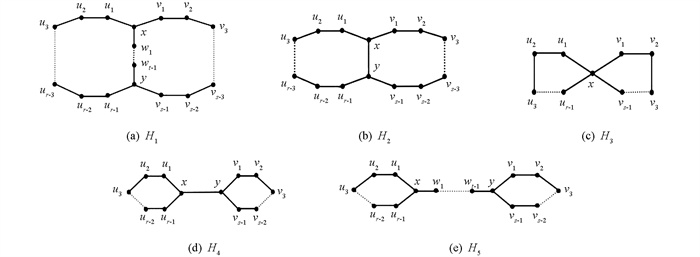
    定义3  设图H是无悬挂点的双圈图，则H∈{H1，H2，H3，H4，H5}.

    引理1[15]  对任意阶数至少为3的图G，有χ'Σ(G)≥Δ(G). 若GΔ≠Ø，则χ'Σ(G)≥Δ(G)+1.

    引理2  若图G有一个圈长恒等于1(mod 3)的圈，且该圈仅有1个3度点，则χ'Σ(G)≥4.

    证  记圈长r(r≡1(mod 3))的圈为C=v1v2…vrv1，且dG(v1)=3，dG(vi)=2(2≤i≤r). 由引理1得，χ'Σ(G)≥3. 假设G有3-NSDPEC，则用1，2，3依次循环染v1v2，…，vr-1vr. 由于边v1v2，vr-1vr分别染1，3，根据正常边染色的条件，vrv1只能染2，则f(vr-1)=f(vr)=5，矛盾. 则χ'Σ(G)≥4.

    引理3(组合零点定理)[16]  设F为任一数域，P=P(x1，x2，…，xn)是F=F[x1，x2，…，xn]上的多项式. 设$\operatorname{dep}(P)=\sum\limits_{i=1}^{n} k_{i} $，其中ki为非负整数，P中x1k1x2k2…xnkn的系数非零. 若S1，S2，…，Sn⊆F且|Si|>ki(1≤i≤n)，则存在s1∈S1，s2∈S2，…，sn∈Sn，使得P(s1，s2，…，sn)≠0.

2.   主要结论

  • 定理1  记树高都为0的双圈图分别为H1，H2，H3，H4，H5(如图 1所示)，则

    证  对于图H1. 记P1=xu1…ur-1y，P2=xv1…vs-1y，P3=xw1…wt-1y，显然这3条路是对称、等价的，且χ'Σ(H1)≥3. 现根据路长r，s，t分别给出H1的$\left(\begin{array}{l} 3 \\ 1 \end{array}\right)+\left(\begin{array}{l} 3 \\ 1 \end{array}\right)\left(\begin{array}{l} 2 \\ 1 \end{array}\right)+\left(\begin{array}{l} 1 \\ 1 \end{array}\right)=10 $种染色(如表 1).

    现需证当r，s≡1(mod 3)，t≡0(mod 3)或r，s≡1(mod 3)，t≡2(mod 3)时，H1无3-NSDPEC.

    反证法：假设当r，s≡1(mod 3)，t≡0(mod 3)时，H1有3-NSDPEC. 不妨令P1依次循环染1，3，2，P3依次循环染3，1，2，路xv1…vs-1依次循环染2，3，1. 因为边yur-1染1，边ywt-1染2，边yvs-1只能染3，则f(vs-1)=f(vs-2)=4，矛盾. 故χ'Σ(H1)≥4. r，s≡1(mod 3)，t≡2(mod 3)时的证明类似. 定理1成立.

    对于图H2. 由引理1得，χ'Σ(H2)≥4. 下面给出H2的一个4-NSDPEC：边xy，yur-1，xv1分别染3，4，4，路xu1u2…ur-1依次循环染2，1，3，路yvs-1vs-2…v1依次循环染1，2，3. 定理1成立.

    对于图H3. 由引理1得，χ'Σ(H3)≥4. 下面给出H3的一个4-NSDPEC：边xur-1，xvs-1分别染2，4，路xu1u2…ur-1依次循环染1，4，3，路xv1v2…vs-1依次循环染3，1，2. 定理1成立.

    对于图H4. 由引理1得χ'Σ(H4)≥4. 下面给出H4的一个4-NSDPEC：边xur-1，xy，yvs-1分别染2，1，4，路xu1u2…ur-1依次循环染4，1，3，路yv1v2…vs-1依次循环染3，1，2. 定理1成立.

    对于图H5. 由引理1得，χ'Σ(H5)≥3.

    若r≡1(mod 3)或s≡1(mod 3). 由引理2知，χ'Σ(H5)≥4. 下面给出H5的一个4-NSDPEC：边xur-1染4，路xu1…ur-1依次循环染3，2，1，边yvs-1染2，路yv1…vs-1依次循环染3，1，4. 边ywt-1染4，路xw1…wt-1依次循环染1，3，2. 定理1成立.

    若r≢1(mod 3)且s≢1(mod 3). 给出H5的一个3-NSDPEC：路xw1…wt-1y依次循环染1，2，3. 令ywt-1染a，且{1，2，3}\{a}={b，c}. 当s≡0(mod 3)时，圈yv1…vs-1y依次循环染c，a，b；当s≡2(mod 3)时，圈yv1…vs-1y依次循环染b，c，a. 圈xu1…ur-1x与yv1…vs-1y的染法相似. 定理1成立.

    将有根树的树高大于0且Δ(G)=3的双圈图分为3种：α-型双圈图，β-型双圈图，γ-型双圈图.

    α-型双圈图：设图G是n阶双圈图(n≥16)，且同时满足：(a) Δ(G)=3，GΔ=Ø；(b) 图G是在H1的基础上连接着树，且在连接(x，y)的3条路中，有任意2条路的路长都恒等于1(mod 3)，另一条路的路长恒等于2(mod 3)；(c) 在路长恒等于2(mod 3)的路中，存在内点z，使得(x，z)与(z，y)的路长均为1(mod 3)；(d) 任意v∈V(H1)\z，dG(v)=dH1(v).

    β-型双圈图：设图G是n阶双圈图(n≥10)，且同时满足：(a) Δ(G)=3，GΔ=Ø；(b) G中存在圈C，该圈圈长为r(r≡1(mod 3))，且圈上仅有1个3度点.

    γ-型双圈图：除α-型双圈图、β-型双圈图之外的Δ(G)=3的n阶(n≥4)双圈图.

    定理2  若图G是α-型双圈图或者β-型双圈图，则χ'Σ(G)=4.

    证  由引理2与定理1的证明可知，不论图G是α-型双圈图还是β-型双圈图，都有χ'Σ(G)≥4.

    情形1   有根树最大高度为1.

    若图G是α-型双圈图. 记路P1的长r≡1(mod 3)，路P2的长s≡1(mod 3)，路P3的长t≡2(mod 3). 在表 1中r，s≡1(mod 3)，t≡2(mod 3)时4-NSDPEC的基础上，给出G的一个4-NSDPEC：因GΔ=Ø，故t≥8. 在H1中，点z与其圈上的2个邻点的色集合分别是{1，2}，{1，3}，{2，3}，则给z的悬挂边染3即可.

    若图G是β-型双圈图. G只能由H5连接悬挂边所得，且悬挂边不可能同时在G的2个圈长都恒为1(mod 3)的圈上，也不可能在圈长为3的圈上，有可能在路w2…wt-2(t≥4)上. 给G增加悬挂边，使G的3条路的所有顶点都有悬挂边(记该图为G0). 在定理1的H5的4-NSDPEC的基础上，给出G0的一个4-NSDPEC：路u2…ur-2上的ui(2≤i≤r-2)的悬挂边染4；路v2…vs-2上的vi(i≡2(mod 3))的悬挂边染3，其他点的悬挂边染2；路w2…wt-2上的wi(2≤i≤t-2)的悬挂边染4.

    现在去掉所有添加的悬挂边，容易得到图G的一个4-NSDPEC.

    情形2   有根树最大高度大于1.

    选树上具有最大高度的路，其悬挂点为v. v的邻点w不在圈上，w仅有一个非悬挂邻点u. 反证法：设G是一个极小反例，即G是Δ(G)=3，且使|V(G)|+|E(G)|最小的不存在4-NSDPEC的图，则G的任意真子图G′有一个4-NSDPEC φ′. 令G′=G-wv，下面在G′的基础上，给边wv染色，将φ′拓展为G的4-NSDPEC φ.

    若dG(w)≠dG(u)，则给边wv正常边染色就会使w与u邻点可区别. 又因为dG(w)≤3，dG′(w)≤2，故在φ′下，w至少有2色未表现，总有一种色给wv，使得w与u邻和可区别，得到G的一个4-NSDPEC. 与G是极小反例矛盾.

    若dG(w)=dG(u)=2，则给边wv染上G′中点u未表现的色，即可使得w与u邻和可区别，得到G的一个4-NSDPEC. 与G是极小反例矛盾.

    综上所述，定理2成立.

    定理3  若图G是γ-型双圈图，则

    证  记图Gi是在Hi的基础上连接有根树得到的双圈图，因为Δ(G)=3，故i≠3.

    情形1   有根树最大高度为1.

    情形1.1   若GΔ=Ø，则G=G1，G5. 由引理1知χ'Σ(G)≥3，下面给出图G的一个3-NSDPEC.

    当G=G1时，根据图H1的3条路的路长，分以下几种情况讨论：

    1) 若H1的3条路的路长是表 1中除r，s≡1(mod 3)，t≡0(mod 3)或r，s≡1(mod 3)，t≡2(mod 3)之外的8种情况，则在定理1中H1的3-NSDPEC的基础上，给G所有悬挂边正常边染色，使G中所有3度点的色集合都是{1，2，3}，即得到G的一个3-NSDPEC.

    2) 若H1的3条路的路长是r，s≡1(mod 3)，t≡0(mod 3)的情况. 图G的悬挂点可以在P1，P2或P3上.

    若P1的点uj(j≠2，r-1)上存在悬挂点，记其中一个悬挂点为v. 给边xu1，u1u2，…，uj-1uj，ujv，ujuj+1，…，ur-1y染$(132)^{\frac{r-1}{3}} 13$，P2染$(231)^{\frac{s-1}{3}} 2$，P3染$(321)^{\frac{t}{3}}$，则S(y)=S(x)={1，2，3}. 若3条路还存在其他悬挂边，则给其正常边染色，使G所有3度点的色集合都是{1，2，3}，即得到G的一个3-NSDPEC.

    若P2的点vj(j≠2，s-1)上存在悬挂点，记其中一个悬挂点为v. 给P1染$(132)^{\frac{r-1}{3}} 1$，边xv1，v1v2，…，vj-1vj，vjv，vjvj+1，…，vs-1y染$(231)^{\frac{s-1}{3}} 23$，P3染$(312)^{\frac{t}{3}}$，则S(y)=S(x)={1，2，3}. 若3条路还存在其他悬挂边，则给其正常边染色，使G所有3度点的色集合都是{1，2，3}，即得到G的一个3-NSDPEC.

    若P3的点wj(j≠2，t-1)上存在悬挂点，记其中一个悬挂点为v. 给P1染$(132)^{\frac{r-1}{3}} 1$，P2染$(231)^{\frac{s-1}{3}} 2$，边xw1，w1w2，…，wj-1wj，wjv，wjwj+1，…，wt-1y染$(312)^{\frac{t}{3}} 3$，则S(y)=S(x)={1，2，3}. 若3条路上还存在其他悬挂边，则给其正常边染色，使G所有3度点的色集合都是{1，2，3}，即得到G的一个3-NSDPEC.

    3) 若图H1的3条路的路长是r，s≡1(mod 3)，t≡2(mod 3)的情况，证明方法与r，s≡1(mod 3)，t≡0(mod 3)的情况类似.

    当G=G5时，方法与G=G1时类似.

    情形1.2   若GΔ≠Ø，则G=G1，G2，G4，G5. 由引理1得χ'Σ(G)≥4. 给图G增加悬挂边，使得图G上的点，除悬挂点外，都是3度点(记该图为G'i(i=1，2，4，5)). 下面在定理1中Hi(i=1，2，4，5)的邻和可区别边染色的基础上，给出图G'i(i=1，2，4，5)的一个4-NSDPEC：

    给出图G'1的一个4-NSDPEC：

    1) 当H1是表 1中除r，s≡1(mod 3)，t≡0(mod 3)或r，s≡1(mod 3)，t≡2(mod 3)外的8种情况时，则给G'1的所有悬挂边染4.

    2) 当H1是r，s≡1(mod 3)，t≡0(mod 3)情况时，给P1上的ur-1的悬挂边染3，其他点的悬挂边染4. 给P2上的vs-1的悬挂边染3，点vi(i≡2(mod 3))的悬挂边染2，其他点的悬挂边染4. 给P3上的wt-1的悬挂边染3，其他点的悬挂边染4.

    3) 当H1是r，s≡1(mod 3)，t≡2(mod 3)的情况时，给wt-1的悬挂边染2，vs-1的悬挂边染1，其他悬挂边染4.

    去掉所有添加的悬挂边，即得到G1的一个4-NSDPEC.

    给出图G'2的一个4-NSDPEC：先看路xu1u2…ur-1y. 当r≡2(mod 3)时，给u1，…，ur-2的悬挂边依次循环染3，4，4，ur-1的悬挂边染1. 特别地，当r=2时，u1的悬挂边染1. 当r≢2(mod 3)时，给u1，…，ur-2的悬挂边依次循环染3，4，4，ur-1的悬挂边染2. 再看路xv1…vs-1y. 当s≡2(mod 3)时，给v1的悬挂边染2，点vs-1，…，v2的悬挂边依次循环染3，4，4. 特别地，当s=2时，v1的悬挂边染2. 当s≢2(mod 3)时，给v1的悬挂边染1，点vs-1，…，v2的悬挂边依次循环染3，4，4.

    去掉所有添加的悬挂边，即得到G2的一个4-NSDPEC. 若G=G4或G=G5，染法类似.

    情形2   有根树的最大高度大于1. 当GΔ=Ø时，χ'Σ(G)≥3；当GΔ≠Ø时，χ'Σ(G)≥4. 反证法：设G是一个极小反例，即G是Δ(G)=3，且使|V(G)|+|E(G)|最小的不存在s-NSDPEC的图，G的任何真子图G′有一个s-NSDPEC φ′. 其中

    选树上有最大高度的路，其悬挂点为v. v的邻点w不在圈上，w仅有一个非悬挂邻点u. 令G′=G-wv，下面在G′的基础上，给wv染色，将φ′拓展为G的s-NSDPEC φ.

    情形2.1   若GΔ=Ø，则χ'Σ(G)≥3.

    当dG(w)≠dG(u)时，若dG(w)=3，则给wv正常边染色，必有fφ(w)≠fφ(u)；若dG(w)=2，则dG′(w)=1，在G′中w有2色未表现，故总有1色给wv，使得fφ(w)≠fφ(u)，从而得到图G的一个3-NSDPEC. 与G是最小反例矛盾.

    当dG(w)=dG(u)时，给wv染上u未在G′表现的色，即得到G的一个3-NSDPEC. 与G是最小反例矛盾.

    情形2.2   若GΔ≠Ø，则χ'Σ(G)≥4.

    当dG(w)≠dG(u)时，因dG(w)≤3，dG′(w)≤2，则在G′中w至少有2色未表现，则总有1色给wv，使得fφ(w)≠fφ(u)，从而得到G的一个4-NSDPEC. 与G是最小反例矛盾.

    当dG(w)=dG(u)，且φ′的点w表现的色都在u上表现时，则给wv染上u未在G′中表现的色，即可得到图G的一个4-NSDPEC. 与G是最小反例矛盾.

    当dG(w)=dG(u)，且φ′的点w表现的某色没在u上表现时，由于dG(w)≤3，dG′(w)≤2，则在G′中w至少有2色未表现，总有1色给wv，使得fφ(w)≠fφ(u)，从而得到G的一个4-NSDPEC. 与G是最小反例矛盾.

    综上所述，定理3成立.

    定理4  若图G是Δ(G)≥4的，且有根树最大高度大于0的双圈图，则

    证  记图Gi是在Hi(1≤i≤5)的基础上连接有根树得到的双圈图.

    情形1   若有根树的最大高度为1，则根据有根树的位置和圈上相邻点的度分3种情况讨论.

    情形1.1   图H上所有2度点z在图G中的度也为2，即dH(z)=dG(z)=2. 则悬挂边只能在x或y处. 不妨设dG(x)=k，dG(y)=l，且k≥l≥1.

    若G=G1，则χ'Σ(G)≥Δ(G)=k+3. 由于G中的H1有4-NSDPEC，则与点y相邻的2度点的色集合的所有元素之和范围是3~7. 显然dG(y)≥3. 当dG(y)=3时，G中y与y的邻点一定邻和可区别；当dG(y)≥4时，f(y)≥10，则对y的悬挂边正常边染色就能使y与y的邻点邻和可区别.

    又因为k≥l≥1，故dG(x)=Δ(G)，则对点x的所有悬挂边正常边染色就能使得点x与x的邻点邻和可区别，即得到图G的一个Δ(G)-NSDPEC.

    当G=Gi(2≤i≤5)时，方法与G=G1类似.

    情形1.2   图H上存在2度点z，使得dH(z)=2且dG(z)≥3，且对任意满足该条件的点z，有dG(z)=dG(z′)=dG(z″). 其中z′，z″是z在H上的2个邻点.

    由于GΔ≠Ø，故χ'Σ(G)≥Δ(G)+1. 反证法：设G是一个极小反例，G的任何真子图G′都有一个(Δ(G)+1)-NSDPEC. 所有满足情形1.2的双圈图G都有结构1(如图 2(a)所示)，且Δ(G)=k+2.

    令G′=G-zz1-zz2，对zz1，zz2重新染色x1，x2. f′(z)表示在G′中z的色集合的所有元素的加和. 边zz1，zz2可用颜色集分别为S1，S2，由正常边染色的条件得

    再由邻和可区别边染色的条件得

    去掉Q(x1，x2)的常数得$Q^{\prime}\left(x_{1}, x_{2}\right)=\left(x_{1}-x_{2}\right)\left(x_{1}+x_{2}\right)^{2}=x_{1}^{3}+x_{1}^{2} x_{2}-x_{1} x_{2}^{2}-x_{2}^{3}$. 因x12x2的系数为1≠0，由引理3，可在S1，S2中选取x1，x2，即得到G的一个(Δ(G)+1)-NSDPEC. 与G是最小反例矛盾.

    情形1.3   图H上存在一个2度点z，使得dH(z)=2且dG(z)≥3，且dG(z)≠dG(z′). 其中z′，z″是点z在H上的2个邻点.

    若GΔ=Ø，则χ'Σ(G)≥Δ(G). 反证法：设G是一个极小反例，则G的任何真子图G′都有一个Δ(G)-NSDPEC.

    1) 当H=H3，Δ(G)=4，且x是G的唯一最大度点时. 令G′=G-zv，zv是悬挂边. 因3度点z与其邻点仅有1+2+3=2+4，1+2+4=3+4邻和相等的情况. 故z与z′，z″的公共边染2，4，导致z最多与一个2度点邻和相等. 在G′的4-NSDPEC的基础上，zv有2色未表现，则总存在1色给zv，得到G的一个4-NSDPEC. 与G是最小反例矛盾.

    2) 其他情况时，令G的最大度点为u，uv是悬挂边. 令G′=G-uv，对uv正常边染色即得到G的一个Δ(G)-NSDPEC. 与G是最小反例矛盾.

    若GΔ≠Ø，则χ'Σ(G)≥Δ(G)+1. 反证法：设G是一个极小反例，则G的任何真子图G′都有一个(Δ(G)+1)-NSDPEC. 由于GΔ≠Ø，当G有1个最大度点在H的2度点上时，则G一定有结构1，证明方法如情形1.2. 当G中最大度点都不在H的2度点上时，即最大度点只能同时在x，y处. 且圈上一定存在点u(u≠x，y)，使得3≤dG(u)≤Δ(G)-1. G一定有结构2(如图 2(b)所示).

    令G′=G-uu1，则对uu1重新染色x1. 记uu1可用颜色集为S1. 由正常边染色的条件得

    再由邻和可区别边染色的条件得

    去掉Q(x1)的常数得到另一个多项式：Q′(x1)=x12.

    由于x12的系数为1≠0，则可在S1中选取满足邻和可区别边染色条件的x1，得到图G的一个(Δ(G)+1)-NSDPEC. 与G是最小反例矛盾.

    情形2   有根树的最大高度大于1.

    当GΔ=Ø时，χ'Σ(G)≥Δ(G)；当GΔ≠Ø时，χ'Σ(G)≥Δ(G)+1. 反证法：设G是一个极小反例，即G是使|V(G)|+|E(G)|最小的不存在s-NSDPEC的图，G的任何真子图G′有一个s-NSDPEC φ′. 其中

    选树上具有最大高度的路，其悬挂点为v. 点v的邻点w不在圈上，且w仅有1个非悬挂邻点u. 令G′=G-wv，下面在G′的基础上，给边wv染色，将φ′拓展为G的s-NSDPEC φ.

    情形2.1   若GΔ=Ø，则χ'Σ(G)≥Δ(G). 下面分3种情况去证明图G有Δ(G)-NSDPEC.

    当dG(w)≠dG(u)时，给wv正常边染色可使Sφ(w)≠Sφ(u). 故给wv染色时，只需考虑fφ(w)与fφ(u)是否相等. 若dG(w)=Δ(G)，给wv正常边染色，必有fφ(w)≠fφ(u)；若dG(w)≤Δ(G)-1，则dG′(w)≤Δ(G)-2，即在G′中w至少有2色未表现，且最多有1色给wv，使得fφ(w)=fφ(u). 故总有1色给wv，使得w与u邻和可区别，从而得到G的一个Δ(G)-NSDPEC. 与G是最小反例矛盾.

    当dG(w)=dG(u)，且φ′的点w表现的色都在u上表现时，给边wv染上点u未在φ′中表现的色，即可得到图G的一个Δ(G)-NSDPEC. 与G是最小反例矛盾.

    当dG(w)=dG(u)，且φ′的点w表现的某色未在u上表现时，由于dG(w)≤Δ(G)-1，则dG′(w)≤Δ(G)-2，即在G′中w至少有2色未表现，且最多有1色给wv，使得fφ(w)=fφ(u). 故总有1色给wv，使得w与u邻和可区别，从而得到G的一个Δ(G)-NSDPEC. 与G是最小反例矛盾.

    情形2.2   若GΔ≠Ø，则χ'Σ(G)≥Δ(G)+1. 证明图G有(Δ(G)+1)-NSDPEC时，证明思路分3种：dG(w)≠dG(u)；dG(w)=dG(u)且φ′的点w表现的色都在点u上表现；dG(w)=dG(u)且φ′的点w表现的某种色没有在点u上表现. 详细过程与情形2.1类似.

    综上所述，定理4成立.

参考文献 (16)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回