收发器消耗的能量用于在传感器处发送和接收数据、发射机电子设备的能量使用、放大过程中的能量耗散和在感知目标时的能量使用. 本文使用e_tx(b，d)，e_rx(b)和e_sx(b)来表示两个距离为d的传感器间链路发送、接收和感测b位数据所消耗的能量.

其中，e_el表示发射机电子设备消耗的能量，e_am表示运行发射器每位消耗的能量，η表示路径损耗指数，取值范围在2~6之间，取决于环境的衰落条件. e_s是感测1比特数据所消耗的能量，发送、接收和感测数据的b比特能量需求可以表示为：

发送、接收和感测b位数据后的剩余能量可以表示为：

其中，e_i表示传感器的初始能量.

设传感区域为a×a的正方形，S={s₁，s₂，…，s_N}为在区域内服从泊松点过程的传感器集合，T={t₁，t₂，…t_n}是在传感区域内服从泊松点过程的n个目标的集合. 当t_i∈T∀i，1≤i≤N时，如果至少存在一个传感器s_j，1≤j≤N使得d(t_i，s_j)≤r，则称T中每个目标被S中的至少一个传感器s_j覆盖，如果s_j∈C_k，则称T被C_k覆盖，其中r为传感器的感测范围，C_k为覆盖集. 设$\lambda=\frac{N}{a^{2}}$是该区域满足上述条件所需传感器的密度，$p(X=x)=e^{-\lambda} \frac{\lambda^{x}}{x !}$为泊松分布的概率分布函数(PDF)，p(x=0)=e^-λ，p(x≥1)=$1-e^{-\frac{N}{a^{2}}}$，可以从上面方程中为p(x≥1)≥0.9选择适当的N值.

感测区域中的传感器形成网络，其中如果d(s_i，s_j)≤R，∀1≤i，j≤N，则两个传感器通过无线链路连接，R表示传输范围. 本文将传感器集合划分为两个不相交的集合S_t和S_r，S_t为覆盖至少一个目标的传感器集合，S_r为不覆盖任何目标的传感器集合. 设C_k⊂S_t∪S_r∀k=1，2，…，N是一组传感器，使T被C_k覆盖和连接，则可以用数学公式表示为：

1) 当t_i∈T∀i，1≤i≤N时，如果至少存在一个传感器j，1≤j≤N使得d(s_i，s_j)≤r和s_j∈C_k，则称T被C_k覆盖.

2) 当t_i∈T∀i，1≤i≤N时，如果存在一组传感器C_kj⊆C_k使得C_k包含来自S_t的仅一个成员和S_r的零个或多个成员，且存在通过这些传感器从汇点到属于S_t传感器的路径，则称T由C连接.

本文需要解决的问题是在保证C_k∀k=1，2，…，N的传感器数量最优和最小化网络整体能耗的情况下，最大限度地减少覆盖集的数量，即寻找可能的最大覆盖数量，其中每个传感器S_i，1≤i≤N仅属于一个覆盖集C_k.

本文将寻找可能最大覆盖数量的问题表述为整数线性规划(Integer Linear Program，ILP)问题. 令C={C₁，C₂，C₃…C_u}表示所有可能的覆盖集集合，每个覆盖集覆盖所有目标.

ILP的目标为：

式(8)的目标函数用来最大化不相交集合的数量，每个集合覆盖所有目标并通过将待激活传感器的数量乘以小的正系数ρ(ρ≤1)来施加约束，从而最小化每个集合中所使用的传感器数目. ILP存在k个变量和(n+k)个约束条件，式(9)规定了传感器至多用于一个覆盖集的条件. 上述ILP公式提供了最优解，但对于大型问题实例是不可行的，本文基于多项式时间算法来逼近问题的解.

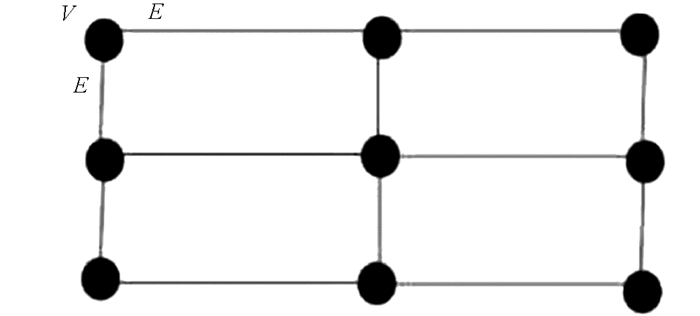
汇聚节点的位置对网络性能有很大影响，因此位置非常重要. 无线传感器网络中汇聚节点的优化定位存在参数多、路由算法不同、涉及大量传感器节点、传感器节点不同能力等诸多挑战. 因为会影响诸如能量消耗、延迟、吞吐量和网络连接等性能指标，汇聚节点定位需要精确地选择汇聚节点的位置. 调整汇聚节点的位置可以提高WSN的可靠性，因为汇聚节点最理想的初始位置可能会由于网络的变化而变得无效. 本文汇聚节点位于目标节点附近，将WSN限制为网状拓扑，如图 1所示. 图 1中黑色圆点表示传感器网络节点. 对系统模型进行如下假设：

1) 所有传感器节点都是静止的，并且位于具有相同大小单元的二维正方形网格中.

2) 所有传感器节点具有相同的初始能量.

3) 范围是固定的，等于网格中两个相邻节点之间的距离，即一跳是一个网格单元边长.

4) 传感器节点通过沿最短路径的多跳将数据中继到汇聚节点.

5) 汇聚节点只能位于网格中的特定位置.

传感器网络可以由点和边组成的图G(V，E)来表示，其中V是传感器节点的顶点，E边缘充当两个相邻节点间的单跳连接. 如果传感器节点通过一跳连接到汇聚节点，那么数据以简单的方式进行转发，否则将通过多跳进行数据转发.

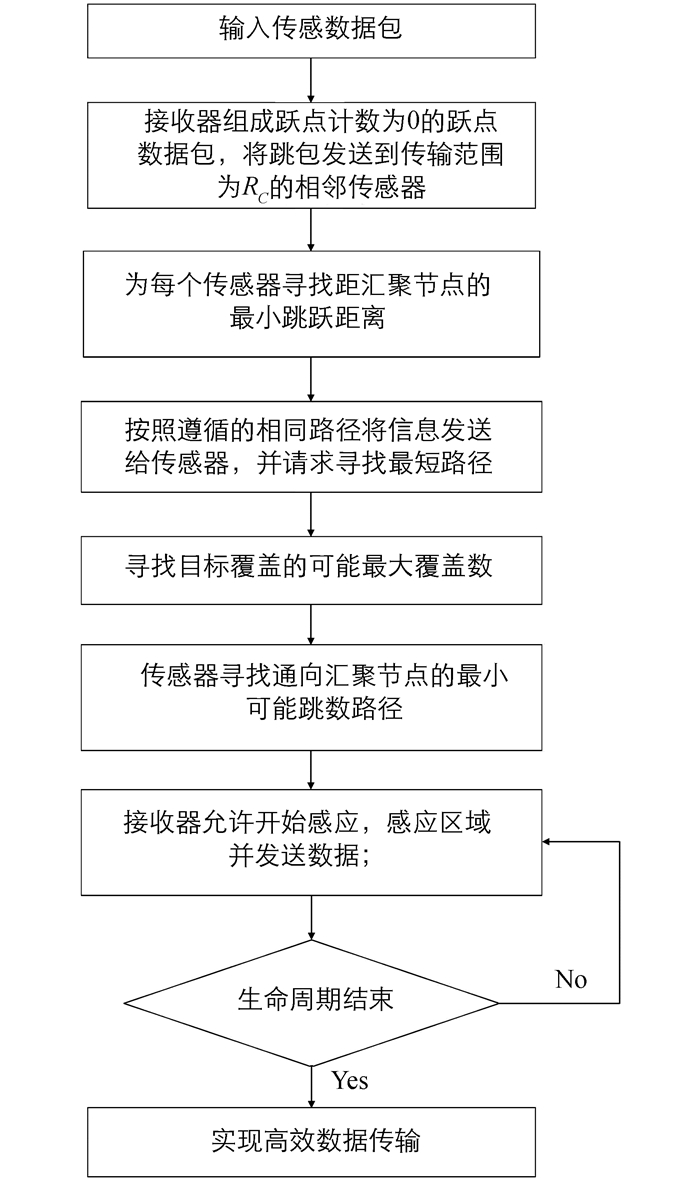
本文提出的算法首先为每个传感器找到距汇聚节点的最小跳跃距离，随后所有目标覆盖传感器都将各自具有目标身份的信息发送到汇聚节点，请求寻找从传感器覆盖目标到汇聚节点使用最小能量的最小跳跃路径. 当所有请求都到达汇聚节点，开始生成目标覆盖传感器的覆盖集. 汇聚节点选择一组不为空的覆盖集，获得应答数据包的传感器开始搜索到汇聚节点的最小可能跳数路径(Minimum Possible Hop Count Path，MPHCP)，汇聚节点按照用于侦听的相同路径向这些传感器发送许可数据包，选定的发送器在获得许可数据包后开始感测. 在重新计算能量后，通过先前找到的最节能路径将生成的数据发送到汇聚节点，一旦这组覆盖集的寿命结束，汇聚节点就为另一组传感器做同样的工作，当完成了所有这样的覆盖集后，汇聚节点就终止感测过程，具体流程如图 2所示.

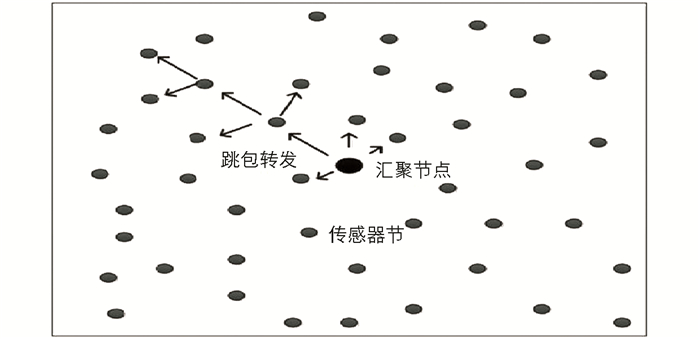
汇聚节点生成一个0跳的跳包，并在其周围的传输范围R_c中转发该数据包. 假设汇聚节点位于感测区域的中间(图 3)，所有传感器都用1跳和初始能量进行初始化，获得跳包的传感器存储跳数和能量的值. 如果跳数小于所存储的跳数值，更新跳数. 传感器在等待一段时间后广播相同的内容，每个传感器中的能量也会根据能耗模型进行更新. 每个相邻节点处的剩余能量也与跳数信息一起被广播到相邻节点，以便传感器具有关于其最小距离和来自汇聚节点最小能量的信息. 在将跳数转发到下一个传感器之前，传感器会将其递增1，这有助于下一个传感器知道从汇聚节点到自身的确切跳数及路由，因为数据包还包含其所经过的传感器ID. 传感器具有关于自身能量、邻居能量、传感器ID和跳数的信息，每个传感器重复此广播和更新过程，直到覆盖整个网络.

传感器存储有关传感器的信息，传感器已向它们发送了具有最小跳数的数据包、每个邻居节点的剩余能量及自身的剩余能量. 用于存储关于跳包信息的表包含以下字段：跳数、传感器身份和剩余能量. 如果某个节点剩余能量相比其他节点严重不足时，不能作为中继节点使用.

跳距的目标是将最小跳数和剩余能量传递给每个传感器，因此必须确保在可能的范围内具有较低跳计数值的传感器必须开始参考数据包，以避免冗余传输并延长使用寿命. 等待时间应该是传感器可用跳数的函数，引入等待时间的曲线可以防止跳包碰撞. 具体表达为：

其中，φ_i是等待时间指数分布的速率参数，λ为传感器密度，hc_i为跳数. D_i是第i个传感器的等待时间，t是均匀随机变量. 为了避免跳包的冲突，必须保证在4πr²范围内一次仅一个传输，即$\varphi_{i} \propto \frac{4 \lambda \pi r^{2}}{N}$，r为区域半径. 此外，φ_i跳数的依赖性可以表示为$\varphi_{i} \propto \frac{1}{h_{i}}$，其中h_i是具有第i个传感器的跳数值. φ_i的最终表达式可由$\varphi_{i}=\frac{4 \lambda {\rm{ \mathsf{ π} }} r^{2}}{N h_{i}}$给出. 第i个传感器的等待时间由以下公式给出：

该算法在线性时间内运行，算法中没有循环，除了传感器的等待时间外，几乎每个传感器都需要恒定的时间来执行数据包转发. 传感器的等待时间由式(12)求得，虽然是指数型，但随着时间t的增加迅速收敛.

该过程由覆盖至少一个目标的所有传感器启动，随后搜索其邻居的列表发送包含其身份及所覆盖目标身份的请求数据包，跳包转发生成最初从汇点到所有传感器的多跳路径池. 为了找到最短路径，传感器总是将请求数据包转发到从中获得最小跳数数据包和高剩余能量的同一传感器，所有收到请求数据包的传感器都会向发送方传感器发送确认. 如果传感器未收到确认，会将数据包重新发送到另一个传感器，该传感器是其列表中下一个最远的传感器.

由于本节只有一个循环在所有传感器上运行，因此本节算法以线性时间运行，不需要任何额外的传输来探索从传感器到接收器的最小跳跃路径. 通过这种方法，可以保证算法运行时除数据感知和信息发送外的能耗最小.

本文基于多项式时间算法来逼近问题的解. 一旦生成覆盖集，就从s_t中移除属于该覆盖集的相应传感器，并且再次按照式(8)和式(9)来求解问题，重复这个过程可迭代地生成所有可能数量的覆盖集. 本文采用贪婪的方法寻找最小成本覆盖集作为上述问题的解决方案，为此选择包含覆盖目标最多并且具有最高能量的传感器. 该算法从左到右遍历传感器覆盖目标的邻接表，如果两个传感器具有相同数量的覆盖目标，则选择那个具有较大能量值的传感器. 将已取走的传感器删除，重复该过程到没有需要删除的传感器为止.

在生成第一个覆盖集后汇聚节点向传感器发送应答数据包允许感测. 按照覆盖集的生成顺序选择允许的传感器组，应答数据包包含数据包要遵循的路径、接收传感器的标识、覆盖集编号和开始感测的时间，应答包遵循的路径与底层传感器请求包的路径保持相同. 通过这种机制，可以节省大量的时间和能量，并且应答包在尽可能短的时间内到达目的地.

所有收到请求应答包的传感器都会启动MPHCP算法. 在该算法下，传感器找到从自身到汇聚节点的最小可能跳数路径，位于覆盖集中的传感器不需要找到这样的路径. 传感器使用MPHCP算法获取应答包的相同路径，此路径是从汇聚节点到传感器的最小可能路径. 之所以说“最小可能”，是因为需要找到从底层传感器到汇聚节点的最短路径，但是路径的任何部分都不应与另一条路径共用，任何传感器只能参与一条路径. 一旦一组传感器找到MPHCP，汇聚节点启动另一组覆盖集开始查找其MPHCP. 在此算法中，已经属于另一条路径的传感器不计入路径查找中.

为了优化路径的能量消耗，传感器从多跳路径池中选择路径，该多跳路径池由跳包从汇聚节点转发到所有传感器. 本文选择具有优化能耗最小跳数的路径进行数据传输. 参与数据包传输、接收和检测目标的路径的所有传感器所消耗的能量e_p表示为：

其中，路径p由h个跳数组成，h个跳数连接p中的1个传感器. 最小化路径p中的跳数意味着最小化路径能量e_p，最小化e_p可设置为优化准则，并表示为：

其中，δ是每跳的平均进度，Max(δ)表示最大单跳距离，并且e_q表示在移除一个或多个跃点之后通过新的路由q从源传感器向汇聚节点传输数据的能量消耗.

最小化路径中的跳数，使得在移除路径中的一个或多个跳数(具有较少跳数的新路由)之后，通过新路由q从源传感器向汇聚节点传输数据所产生的能量消耗小于现有路由p的能耗. 本文通过最大化朝向汇聚节点的单跳进度来最小化跳数. 路径中的平均单跳距离E(s)和平均跳数E(c)由以下公式给出：

其中，a是正方形传感区域的边长，$\lambda=\frac{N}{a^{2}}$是传感器的密度，r_max是传感器的最大传输范围.

根据本文提出的能量模型，传感器在发射、接收和感知目标时消耗能量，传输过程中消耗的能量是发送方传感器和接收方传感器之间距离的幂. 在两个相邻传感器之间传输b比特数据，每跳的平均能量消耗E(e_t(b，d))可以表示为：

因此，参与包传输、接收和检测目标的路径中所有传感器消耗的平均能量E(e_p)可以表示为：

在本文所提出的算法中，当汇聚节点生成一个跳包时，汇聚节点只发送一次信标，其计数值为0，并且在跳距算法的初始化阶段将其转发到周围的传输范围，从而循环关于其跳计数值1和初始能量的信息. 在发送请求阶段，不需要发送额外的协调消息. 在发送请求阶段，每个传感器节点将请求数据包转发到获得最小跳数数据包的同一传感器，并为ACK发送一次信标进行确认. 应答包遵循的路径与传感器请求包的路径保持相同，这将节省时间和能量，并且使应答包在尽可能短的时间内到达目的地. 由于发送或接收单个数据包而消耗的能量几乎与传感器之间传递的指令数量相同，当考虑实际的传感器网络时，由于竞争而导致的重传将能量消耗提高到很高的水平，甚至发送消息. 因此，在本文提出的协议中传输消息数量非常少，这对于最小化能量消耗和延长系统寿命是可取的. 与减少通信开销所节省的能量相比，复杂计算所消耗的任何额外能量都可以忽略不计.

本文在MATLAB中开发的模拟器中生成了模拟场景，模拟器由传感器部署模块、拓扑生成模块等不同模块组成，模拟了一个由400个传感器节点按照泊松点过程随机分布的网络，每个传感器的感应范围为10 m，传输范围为50 m. 每次模拟运行20次，取平均值来计算结果，每个目标生成1 kb的恒定数据流量. 本文算法的仿真参数如表 1所示. 将实验结果与文献[13]中提到的优化连接覆盖集启发式(Optimized Connected Coverage Heuristic，OCCH)算法和文献[14]中提到的通信加权贪婪覆盖(Communication Weighted Greedy Cover，CWGC)算法进行分析和比较，OCCH和CWGC算法以能够覆盖所有目标的贪婪方式选择源，生成到信宿的最短路由路径，并更新通信开销避免选择具有低剩余能量的节点，因此选择这两个算法与本文算法进行比较分析.

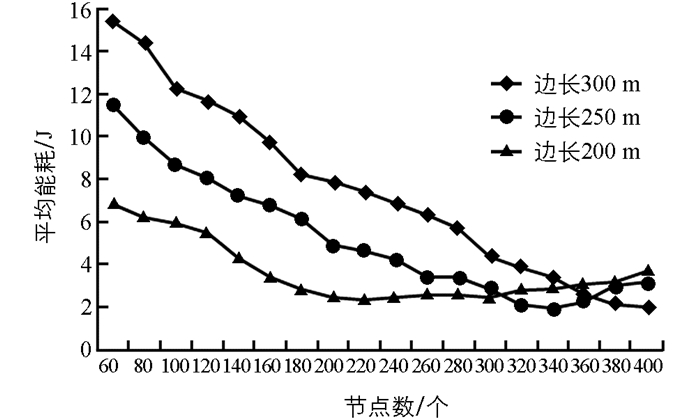
图 4给出了在边长为200 m，250 m和300 m的网络区域中部署30个目标、传感器从50~400个变化时，本文算法的平均能耗. 在本实验中，平均能耗包括为满足覆盖性和连接性要求而花费的能量.

由图 4可以看出，在边长为200 m的网络区域中部署200~225个传感器的能耗最小，边长为250 m的网络区域中部署325~350个传感器的能耗最小，在边长为300 m的网络区域中部署375~400个传感器的能耗最小. 因此，实现最小能耗的传感器数量随着边长增加而增加，这是因为平均单跳距离随着网络面积增加而增加，传输的能量需求是任意两个相邻传感器之间距离因子的幂.

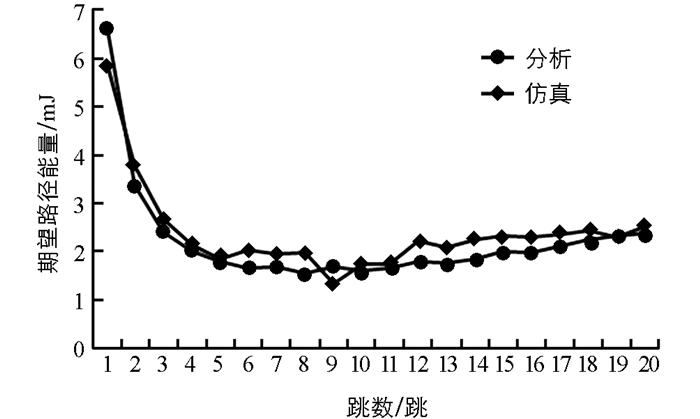
图 5给出了期望路径能量相对于跳数的分析结果. 期望路径能量定义为所有参与传输、接收和感知路径的传感器节点所消耗的能量. 该模拟使用30个随机部署的目标，传感器数量从50~300个变化. 由图 5可以看出，在较少的跳数下路径节点消耗的能量要高得多. 当跳跃从10增加到20时，路径能量增加. 这是因为每跳距离随着跳数增加而减小，需要更多的多跳传输，从而消耗了更多的能量. 对于5~10个跳数，路径能量保持最小. 因此，应该首先考虑5~10跳范围内的替代节能路由.

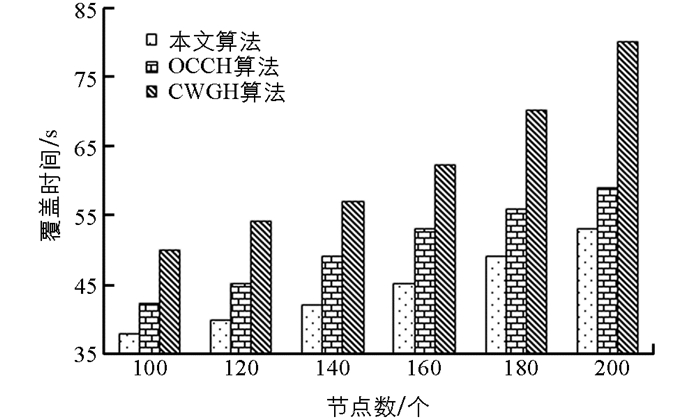
覆盖时间定义为生成所有可能的覆盖集所需的时间. 图 6给出了节点数不同时各算法的覆盖时间，覆盖时间表示为生成所有可能的覆盖集所需的时间.

由图 6可以看出，覆盖时间随着节点密度增加而增加，这是因为当节点密度增加时，重复执行相同操作所消耗的时间增加. 本文算法的性能比OCCH和CWGC好，这是因为本文算法首先为每个传感器找到距汇聚节点的最小跳跃距离，然后请求寻找从传感器覆盖目标到汇聚节点使用最小能量的最小跳跃路径，最后获得应答数据包的传感器开始搜索到汇聚节点的最小可能跳数路径. 通过这种机制，可以节省大量的时间和能量.

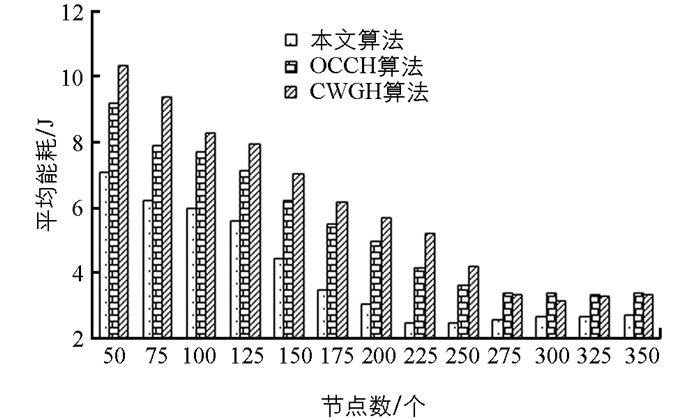
图 7给出了节点数不同时各算法的平均能量消耗. 平均能耗是网络中所有传感器总能耗与传感器数量的比率，包含传感器在满足覆盖性和连通性要求时所消耗的能量. 由图 7可以看出，平均能耗随着传感器数量的增加而下降，这是因为任何两个传感器之间的平均距离随传感器数量的增加而减小，所消耗的能量也随之减少. 本文算法的平均能量消耗低于OCCH和CWGC，这是因为本文算法除了采用最小跳跃距离、最小跳跃路径和最小可能跳数路径这种机制进行数据传输外，另外采用贪婪的方法寻找最小成本覆盖集，包含覆盖目标最多并且具有最高能量的传感器，节省了大量能量.

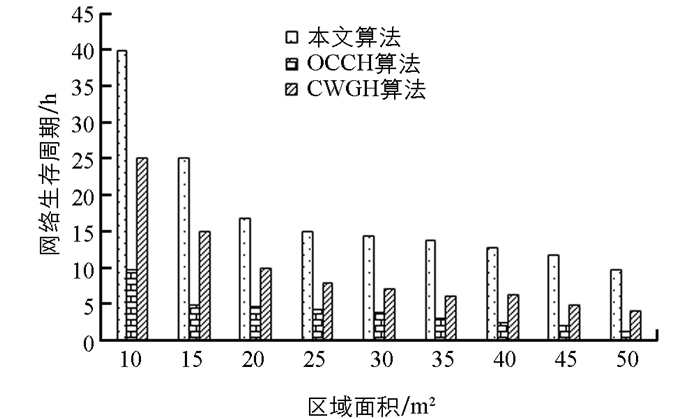
网络生存周期是指一个目标不能被任何传感器节点监控或任何传感器节点不能再将数据转发到接收器的持续时间. 图 8给出了在由300个传感器和30个目标组成的WSN环境下，本文算法与OCCH算法和CWGC算法的网络寿命随区域面积的变化情况.

由图 8可以看出，通信距离随着面积的增加而增加，导致传感节点的密度降低. 由于节点密度降低，网络可靠性降低，导致吞吐量降低和通信开销增加，使得各算法对区域变化敏感. 本文算法在网络生命周期方面比其他两个算法高出20%~30%.

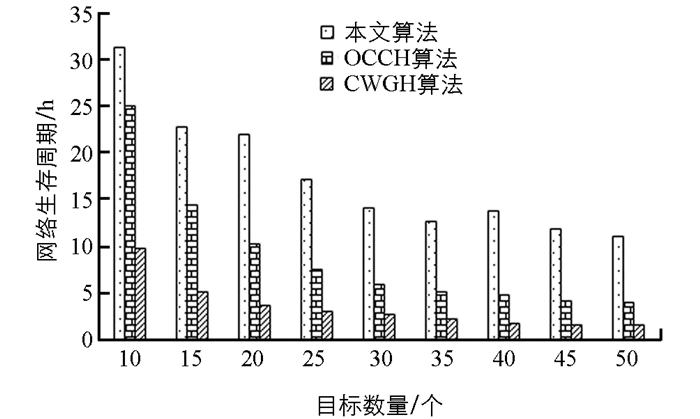
图 9给出了在由300个传感器和面积为200×200 m²组成的WSN环境下，本文算法与OCCH算法和CWGC算法的网络寿命随目标数量的变化情况. 由图 9可以看出，网络寿命随着目标数量的增加而缩短，这是因为随着网络中放置目标数量增加，需要更多的传感器处于活动状态，并且由于数据量的增加，通信量负载也会加重. 本文算法在不同目标数量的网络生存周期比OCCH和CWGC高出近20%.

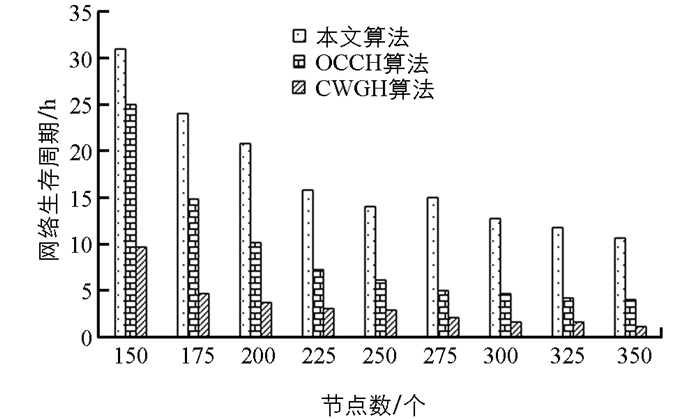
图 10给出了在固定面积和目标的情况下，本文算法与OCCH算法和CWGC算法的网络寿命随传感器数量的变化情况. 由图 10可以看出，网络寿命随节点密度增加而减少，OCCH算法和CWGC算法的网络寿命较短. 本文提出的算法DCCA比在不同节点数的网络生存周期OCCH和CWGC高出近50%.

图 9和图 10中本文算法性能都优于OCCH和CWGC算法. 这是因为本文算法在发送请求阶段，每个传感器节点将请求数据包转发到获得最小跳数数据包的同一传感器，并为ACK发送一次信标进行确认. 应答包遵循的路径与传感器请求包的路径保持相同，并且应答包在尽可能短的时间内到达目的地，减少了冗余，节省了通信开销. 而OCCH和CWGC使用公共节点通过增加关键节点的通信权重来中继数据，增加了通信开销.

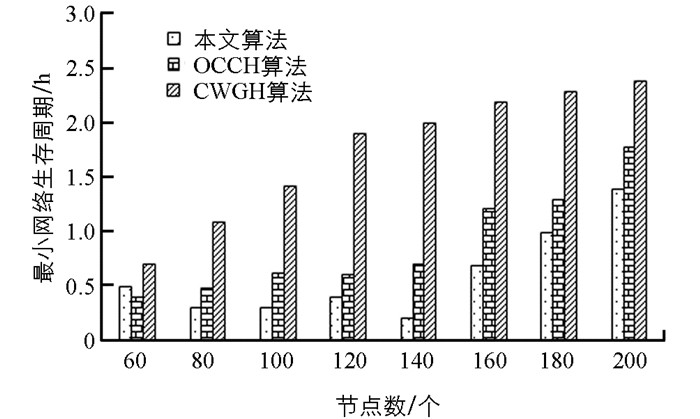
图 11给出了3种算法在区域200×200 m²网络字段中部署的节点数量的最小网络寿命，数据由20个模拟生成. 由图 11可以看出，最小网络生存周期随着节点数量增加而增加. 与OCCH和CWGC算法相比，本文算法的最小网络生存周期优于所对比的方法. 当节点比较多时，本文算法的可扩展性优于OCCH和CWGC算法. 这是因为算法的性能与网络拓扑结构有关，增加节点数量会削弱这种影响.

为了延长网络寿命和降低WSN的平均能耗，本文提出一种高效的无线传感器网络目标覆盖算法. 该算法通过生成不相交的覆盖集来延长覆盖的持续时间，通过提供多个覆盖集来使传感器消耗的能量相当，达到最大化使用寿命的目的，并跟踪传感器正在监控的目标数量及剩余能量寻找从信源到信宿的最小能量路径为感测数据提供扩展的连接性. 实验表明，在节点数为200时，本文方法的覆盖时间为63 s，OCCH算法为60 s，CWGC算法为80 s；本文方法的平均能耗为3 J，OCCH算法为5.5 J，CWGC算法为6.3 J；本文方法的网络生存周期为22 h，OCCH算法为10 h，CWGC算法为4 h. 由此，说明本文方法性能优于OCCH算法和CWGC算法. 另外，不同面积和不同目标的实验结果也表明了本文方法的优越性. 未来的工作是评估分布式环境中的目标覆盖，并将其用于其他类型的覆盖问题，例如区域覆盖或k-覆盖问题.