高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

基于分组量化的高效超维计算分类方法

, 

上一篇

下一篇

姚晓芳, 田波. 基于分组量化的高效超维计算分类方法[J]. 西南大学学报（自然科学版）, 2022, 44(9): 197-204. doi: 10.13718/j.cnki.xdzk.2022.09.020
引用本文: 姚晓芳, 田波. 基于分组量化的高效超维计算分类方法[J]. 西南大学学报（自然科学版）, 2022, 44(9): 197-204. doi: 10.13718/j.cnki.xdzk.2022.09.020
shu
YAO Xiaofang, TIAN Bo. Efficient Hyperdimensional Computing Classification Method Based on Grouping Quantization[J]. Journal of Southwest University Natural Science Edition, 2022, 44(9): 197-204. doi: 10.13718/j.cnki.xdzk.2022.09.020
Citation: YAO Xiaofang, TIAN Bo. Efficient Hyperdimensional Computing Classification Method Based on Grouping Quantization[J]. Journal of Southwest University Natural Science Edition, 2022, 44(9): 197-204. doi: 10.13718/j.cnki.xdzk.2022.09.020
shu

基于分组量化的高效超维计算分类方法

  • 铜仁学院 大数据学院 计算机科学系，贵州 铜仁 554300

  • 基金项目: 国家自然科学基金项目(61741214)；贵州省科技厅基础研究项目(黔科合基础[2020]1Y260)；铜仁市科技局项目(铜市科研[2018]17号)
详细信息
    作者简介:

    姚晓芳，硕士，讲师，主要从事计算机应用技术、软件工程的研究 .

  • 中图分类号: TP393

Efficient Hyperdimensional Computing Classification Method Based on Grouping Quantization

  • Department of Computer Science, School of Big Data, Tongren University, Tongren, Guizhou 554300, China

  • 摘要: 针对当前超维计算(hyperdimensional computing，HD)中大多数方法计算量大、效率低的问题，提出了一种基于分组量化的高效超维计算分类方法，在保证准确性的情况下提高HD模型的计算效率. 该方法首先使用点积操作替代余弦相似度运算来降低HD计算推理阶段的计算量；其次，考虑到查询超向量的相似度计算随着类数的增加而增加，设计了一个分组查询方案，通过检查类的子集来减少相似度计算；最后，使用双值2次幂的量化方式来消除推理阶段的乘法运算，进一步提高计算速度. 实验结果表明，与其他HD计算模型相比，所提方法性能优良，在相同的精度水平下，明显降低了能耗和执行时间.
    Abstract: Aiming at the problem of large amount of calculation and low efficiency of most methods used in current hyperdimensional computing (HD), an efficient hyperdimensional computing classification method based on grouping quantization was proposed, which could improve the computational efficiency of the HD model while ensuring the accuracy of calculation. Firstly, the method used dot product operation instead of cosine similarity operation to reduce the amount of calculation in HD computing reasoning stage. Secondly, considering the similarity calculation of query super vector increasing with the increase of the number of classes, a grouping query scheme was designed to reduce the similarity calculation by checking the subset of classes. Finally, the double value 2-power quantization method was used to eliminate the multiplication in reasoning stage, and further improved the calculation speed. Experimental results show that compared with other HD computing models, the proposed method achieved the best performance and significant reduction in the energy consumption and execution time at the same accuracy level.
  • 加载中

  • 图 1  超维计算的基本流程

    下载: 全尺寸图片 幻灯片

    图 2  所提方法的具体流程

    下载: 全尺寸图片 幻灯片

    图 3  分组量化对HD计算模型分类准确性影响

    下载: 全尺寸图片 幻灯片

    图 4  所提方法在每个阶段的能量消耗和执行时间

    下载: 全尺寸图片 幻灯片

    图 5  不同HD方法的准确度对比

    下载: 全尺寸图片 幻灯片

    图 6  不同HD方法的执行时间对比

    下载: 全尺寸图片 幻灯片
  • [1] IMANI M, MORRIS J, MESSERLY J, et al. BRIC: Locality-Based Encoding for Energy-Efficient Brain-Inspired Hyperdimensional Computing[C] // Proceedings of the 56th Annual Design Automation Conference 2019. Las Vegas: ACM, 2019: 1-6.
    [2] KARUNARATNE G, LE GALLO M, CHERUBINI G, et al. In-Memory Hyperdimensional Computing[J]. Nature Electronics, 2020, 3(6): 327-337. doi: 10.1038/s41928-020-0410-3
    [3] 李翠锦, 瞿中. 基于卷积神经网络的跨层融合边缘检测算法[J]. 计算机应用研究, 2021, 38(7): 2183-2187. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-JSYJ202107051.htm
    [4] GE L L, PARHI K K. Classification Using Hyperdimensional Computing: A Review[J]. IEEE Circuits and Systems Magazine, 2020, 20(2): 30-47. doi: 10.1109/MCAS.2020.2988388
    [5] KHALEGHI B, SALAMAT S, THOMAS A, et al. SHEARer: Highly-Efficient Hyperdimensional Computing by Software-Hardware Enabled Multifold Approximation[C] //ISLPED '20: Proceedings of the ACM/IEEE International Symposium on Low Power Electronics and Design. New York: IEEE Computer Society Press, 2020: 241-246.
    [6] MOIN A, ZHOU A, BENATTI S, et al. Analysis of Contraction Effort Level in EMG-Based Gesture Recognition Using Hyperdimensional Computing[C] //2019 IEEE Biomedical Circuits and Systems Conference (BioCAS). New York: IEEE Computer Society Press, 2019: 1-4.
    [7] IMANI M, MORRIS J, BOSCH S, et al. AdaptHD: Adaptive Efficient Training for Brain-Inspired Hyperdimensional Computing[C] //2019 IEEE Biomedical Circuits and Systems Conference (BioCAS). New York: IEEE Computer Society Press, 2019: 1-4.
    [8] IMANI M, YIN X Z, MESSERLY J, et al. SearcHD: a Memory-Centric Hyperdimensional Computing with Stochastic Training[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2020, 39(10): 2422-2433. doi: 10.1109/TCAD.2019.2952544
    [9] MORRIS J, IMANI M, BOSCH S, et al. CompHD: Efficient Hyperdimensional Computing Using Model Compression[C] //2019 IEEE/ACM International Symposium on Low Power Electronics and Design (ISLPED). New York: IEEE Computer Society Press, 2019: 1-6.
    [10] CHANG E J, RAHIMI A, BENINI L, et al. Hyperdimensional Computing-Based Multimodality Emotion Recognition with Physiological Signals[C] //2019 IEEE International Conference on Artificial Intelligence Circuits and Systems. New York: IEEE Computer Society Press, 2019: 137-141.
    [11] CHENG Y C, YU C C, WU A Y. Task-Projected Hyperdimensional Computing for Multi-Task Learning[C] //The 16th IFIP International Conference on Artificial Intelligence Applications and Innovations(AIAI). Berlin: Springer, 2020: 241-251.
    [12] IMANI M, MESSERLY J, WU F, et al. A Binary Learning Framework for Hyperdimensional Computing[C] //2019 Design, Automation & Test in Europe Conference & Exhibition (DATE). New York: IEEE Computer Society Press, 2019: 126-131.
    [13] XIA K, HUANG J G, WANG H Y. LSTM-CNN Architecture for Human Activity Recognition[J]. IEEE Access, 2020, 8: 56855-56866. doi: 10.1109/ACCESS.2020.2982225
    [14] CHUANG Y C, CHANG C Y, WU A Y A. Dynamic Hyperdimensional Computing for Improving Accuracy-Energy Efficiency Trade-Offs[C] //2020 IEEE Workshop on Signal Processing Systems (SiPS). New York: IEEE Computer Society Press, 2020: 1-5.
  • 加载中
图( 6)
计量
  • 文章访问数:  654
  • HTML全文浏览数:  654
  • PDF下载数:  291
  • 施引文献:  0
出版历程
  • 收稿日期:  2021-07-06
  • 刊出日期:  2022-09-20

基于分组量化的高效超维计算分类方法

    作者简介: 姚晓芳，硕士，讲师，主要从事计算机应用技术、软件工程的研究
  • 铜仁学院 大数据学院 计算机科学系，贵州 铜仁 554300
  • 收稿日期:  2021-07-06
基金项目:  国家自然科学基金项目(61741214)；贵州省科技厅基础研究项目(黔科合基础[2020]1Y260)；铜仁市科技局项目(铜市科研[2018]17号)

摘要: 针对当前超维计算(hyperdimensional computing，HD)中大多数方法计算量大、效率低的问题，提出了一种基于分组量化的高效超维计算分类方法，在保证准确性的情况下提高HD模型的计算效率. 该方法首先使用点积操作替代余弦相似度运算来降低HD计算推理阶段的计算量；其次，考虑到查询超向量的相似度计算随着类数的增加而增加，设计了一个分组查询方案，通过检查类的子集来减少相似度计算；最后，使用双值2次幂的量化方式来消除推理阶段的乘法运算，进一步提高计算速度. 实验结果表明，与其他HD计算模型相比，所提方法性能优良，在相同的精度水平下，明显降低了能耗和执行时间.

English Abstract

    全文HTML

  • 开放科学（资源服务）标志码（OSID）：

  • 类脑超维计算(brain-inspired hyperdimensional computing，HD)通过模拟大脑的工作原理进行建模，使用神经活动模式进行计算，并通过定义良好的向量空间操作在超维空间中处理认知任务[1]. HD计算通过使用高维空间中的向量(超向量)进行计算来模拟认知任务，以替代传统的确定性计算，其中超向量是独立且分布相同的伪随机向量，超向量的维数通常是数万的范围[2]. HD计算作为一种高效节能的快速学习计算范式，在学习和分类任务中具有学习能力强、计算效率和准确性高的优点[3]，在面部检测、语言和手势识别、文本分类、脑机接口等实际应用中大获成功[4-5].

    HD计算和传统计算技术之间的主要区别在于表示数据的方式，因为HD计算将数据表示为近似模式，可以非常有效地对数据进行缩放. HD由编码器和关联存储器组成. 编码器块将输入数据映射到高维向量，并将它们组合以为每个现有类别生成一个模型. 在推理期间，关联存储器通过查看输入超向量与每个存储的模型超向量的相似性来执行推理任务. HD计算支持单次通过训练[6]. 但是，在实际分类问题上，使用单次训练的HD计算模型分类准确性明显较低. 为了解决HD计算在训练迭代上缺乏可控性的问题，文献[7]提出了一种基于高清计算的自适应学习方法，通过引入基于动态学习率的自适应训练方法来解决HD训练问题. 此外，HD计算的分类精度还与模型大小有关，当模型大小增加后，能够增加模型的信息存储能力，从而获得更好的分类效果[8]. 但是，当模型尺寸变大时，计算成本会相应增加，并且随着类的数量而快速增长. 文献[9]为了解决这个问题，提出了一种新颖的压缩方法，利用高维空间的数学原理将超向量压缩为较短的向量，同时保留全长超向量的信息，从而实现了在压缩HD模型尺寸的同时，保持原始模型准确性的目标. 作为一种轻量级算法，HD计算在物联网的边缘计算等许多需要低功耗设计的领域中也取得了较好的效果. 但是，当将其应用于多任务学习(multi-task learning，MTL)时，HD计算的内存开销会随着MTL方案下的任务数量而显著增加[10]. 文献[11]提出了任务投影HD计算方法，通过利用超空间中的冗余维数使HD模型同时支持多个任务. 此外，为了降低关联搜索时的计算量，文献[12]试图对超维计算模型进行二值化处理，这种方法简化了与汉明距离测量的余弦相似度，使得HD能够在硬件中更快、更高效地运行. 然而，二值化的整数模型造成了HD分类准确度下降幅度较大，从而迫使HD使用余弦相似度来提高精度，这在嵌入式设备上运行时会产生巨大的成本.

    针对上述HD计算模型所遇到的问题，本文提出了一个基于分组量化的HD计算框架，用于减少模型计算的复杂度和能耗. 所提出的HD框架利用高维空间中的点积运算代替余弦相似，并且按照相似度将类超向量分为多个子集，以分组的方式减少推理阶段所需的计算量. 此外，通过将训练的HD模型中的值量化为2次幂的形式消除相似性检查中的乘法运算，进一步降低计算的复杂度. 为了保证分类准确度，本文还设计了量化检查，将量化与训练过程结合起来，使HD模型适应量化值.

1.   超维计算

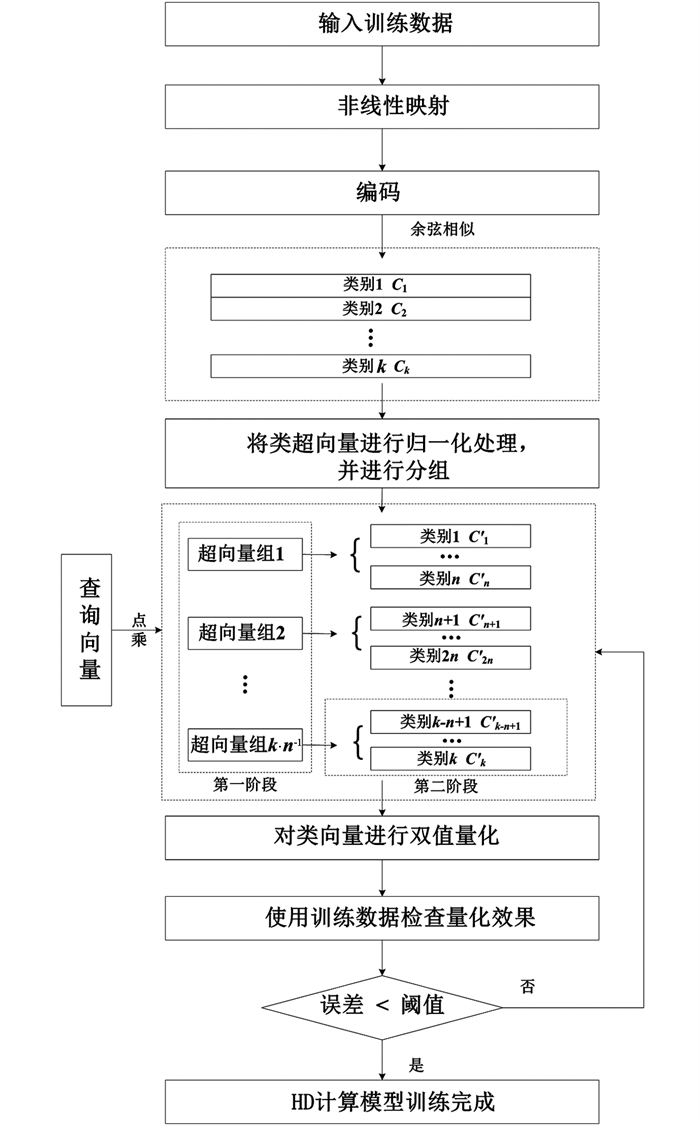
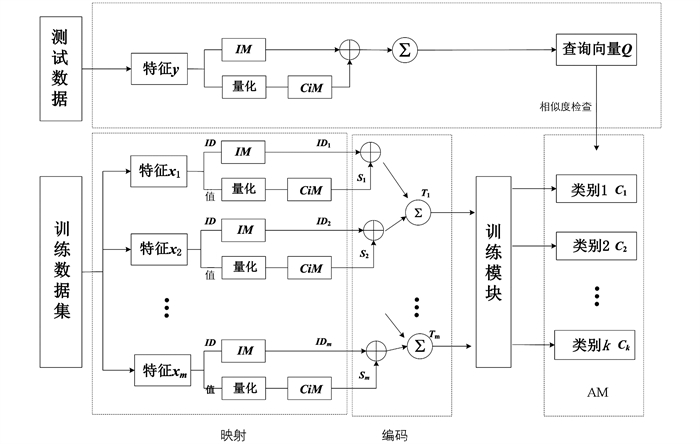
  • 受到人脑神经活动模式的启发，HD计算使用超向量的概念，其维数在数万左右. 作为一种新兴的计算方法，HD计算主要用于解决认知任务问题，具有学习速度快、能量效率高、任务分类精度高等优点. HD计算对输入的超向量执行乘法、加法和置换3个操作，用于转换数据. 这些输入的超向量预先存储在项目存储器中，以形成关联或连接. 在分类问题中，首先在训练阶段训练与类关联的超向量；然后在测试阶段将测试超向量与类超向量进行比较. 从训练数据中生成的超向量称为类超向量，并存储在关联内存中，从测试数据生成的超向量称为查询超向量. 执行关联搜索以预测给定查询超向量的类别. HD计算的基本流程分为非线性映射、编码、训练、分类4个步骤，如图 1所示.

    第1步是非线性映射. 映射的主要目的是将特征向量x投影到具有d维的HD向量上，其中$x \in \mathbb{R}^m$具有m个分量. 特征标识符ID作为一个基本字段，特征的实际值作为该字段的填充值. HD计算从构建项目内存IM和连续项内存CiM开始. IM={ID1，ID2，…，IDm}，其中IDk∈(-1，1)d，k∈{1，2，…，m}对应于第k个特征分量的ID. 当d足够大时，IM中任意两个不同的HD向量几乎正交，即

    式中：Cos(·)和Ham(·)分别是两个向量之间的余弦相似度量和归一化汉明距离.

    连续项内存CiM在HD计算中作为函数实际值的查找表. 建立CiM的过程首先找到每个特征的最大值Vmax和最小值Vmin；然后，将Vmax和Vmin之间的范围量化为l个层次，即L1∈(-1，1)d对应Vmin，Ll∈(-1，1)d对应Vmax，CiM中的每个向量对应于一个实际值范围. 因此，CiM={L1，L2，…，Ll}，其中Lk∈(-1，1)d，k∈{1，2，…，l}. 根据两个HD向量对应值的差异，通过调整Li和Lj之间的汉明距离来保持空间的层次关系. 换言之，特征分量的每个值采用量化的方式与Lk形成关联，并以此在CiM中查找对应的向量{S1，S2，…，Sm}，实现了每个特征值到超空间的非线性映射. 在将数据的每个特征分量映射到HD向量之后，向量对集合I={(ID1，S1)，(ID2，S2)，…，(IDm，Sm)}可以在向量空间操作的下一阶段中极为容易地查询和使用.

    第2步是编码. 在编码过程中，模型首先对I中的每两个向量对执行绑定操作，即两个HD向量之间进行逻辑按位异或操作，如果两个HD向量的值不相同，则异或结果为1，否则，异或结果为0. HD向量绑定操作之后，采用位加法聚合集合I中的m个HD向量. 最后，对聚合结果进行二值化处理，二值化后的HD向量可以表示为T∈(-1，1)d. 整个编码过程可以表述为

    第3步是训练. 所有训练样本经过前两个阶段，得到的向量T被发送到联想存储器(associative memory，AM)进行训练. 对于第i类，同一类的训练样本得到的向量Ti进行聚合以形成一个HD类向量：

    式中：ni表示第i个类的训练样本数. 对于k类分类任务，AM包括k类HD向量，表示为{C1，C2，…，Ck}.

    第4步是分类. 在推理中，HD使用编码和关联搜索进行分类. 首先，HD使用与训练模块相同的映射和编码将测试数据点映射到查询超向量Q∈(-1，1)d. 在HD空间中，相似性度量用于确定查询超向量Q与每个类超向量Ci之间的匹配强度. HD计算中最常用的度量是余弦相似度：

    在查询器超向量Q和分类器中的每个类别超向量之间计算余弦相似度后，选择具有最高余弦相似度的类别作为输出类别.

2.   基于分组量化的超维计算

  • HD计算在对具有k个类的d维模型进行推理时，余弦相似度在查询和类超向量之间需要执行k×d次乘法和加法. 对于资源有限的嵌入式设备而言，关联搜索的计算量是巨大的. 一种解决方案是降低HD模型的维数. 该方法有效地减少了模型尺寸和推理运算次数，从而提高了计算效率. 然而，降低维度会导致精度的下降. 此外，还有学者试图对高清模型进行二值化处理，通过简化与汉明距离测量的余弦相似度来提高计算速度，但是该方法仍以牺牲精度为代价.

    本文的目标是设计一个框架，该框架能够在不影响分类精度的情况下提高HD计算的效率. 为了实现这一目标，提出了一种基于分组量化的HD计算方法，该方法在原始HD计算模型的基础上进行了改进：首先，将余弦相似度计算简化为查询和类超向量之间的点积操作；其次，在HD计算模型中添加一个类别层，以分组搜索方式减少推理计算所需的操作数量；最后，对训练后的HD模型进行量化，利用两个权值的幂来消除相似性检查中的乘法运算. 图 2给出了所提方法的具体流程.

    图 2显示了分组超向量的HD训练和推理过程. 在训练阶段，首先训练一个普通的高清计算模型，其中每个超向量代表一个现有的类，并对超向量进行归一化$\frac{\boldsymbol{C}_i}{\left\|\boldsymbol{C}_i\right\|}$；其次，检查超向量的相似性，以便对类进行分组. 在相似性检查期间，查询超向量是所有类的公共向量，而且HD的目标是找到最大的相对相似度，而不是精确的余弦值. 此外，向量的点积与它们夹角的余弦成正比，点积越大，说明夹角越小，对应的相似度越大. 因此，为了降低计算量，可以采用点积的方式计算，即(4)式可以修改为：

    然后，将n类超向量分组为一个超向量组，得到$\frac{k}{n}$个超向量组，并将$\frac{k}{n}$个超向量组存储到分类阶段. 分组是通过成对检查类超向量的相似性并合并具有最高相似性的类来实现的. 最后，对分组模型的值进行量化.

    • 2.1.   分组量化方法

  • 尽管点击降低了关联搜索的计算量，但这种相似性检查仍涉及许多计算，且随着类的数量线性增加. 为了解决这个问题，本文首先对超向量进行了分组，根据训练的类超向量的相似性将它们分为$\frac{k}{n}$个超向量组；然后将关联搜索分为两个阶段：第一阶段是在$\frac{k}{n}$个超向量组$\left\{\boldsymbol{C}_j^{\text {group }} \mid j=1, \cdots, \frac{k}{n}\right\}$中进行搜索，标识查询超向量所属的类组；第二阶段是在查询超向量所属的超向量组中进行搜索，找到最大相似度的类超向量Ci进行类别输出.

    尽管对类超向量进行分组减少了计算量，但点积相似性检查仍然具有许多昂贵的乘法. 为了进一步降低HD计算的复杂度，考虑对每个类值采用单值量化为2次幂的近似值(2i，$i \in \mathbb{Z}$)，使用移位操作来消除乘法运算. 但是，这种量化方式存在一个缺点，当类别值位于2i-1和2i之间时，会导致HD计算引入较大的误差. 误差的大小取决于类的数量以及类的相似程度. 对于具有许多类别或高度相关的类超向量的应用程序，此量化方式可能会降低分类的准确性. 为克服这一缺点，本文提出了一种更精确的量化方法，该方法将每个类元素分配给两个值的2次幂组合(2i+ 2j，$i, j \in \mathbb{Z}$)，从而将每个训练的类别元素分配给一个更接近实际元素的值，实现更精确的量化，同时对精度的影响也得到相应降低. 该策略通过使用两个移位和单个加法运算来实现乘法运算，提高了计算效率.

    • 2.2.   迭代训练

  • 由于类超向量是高度相关的，因此即使这种量化方法也会对分类精度产生很大影响. 当HD模型在没有经过训练的情况下使用量化值，可能会因为引入误差而降低模型的性能. 为了确保最小的性能损失，本文设计了迭代训练的方式来减少量化可能带来的性能损失.

    如图 2所示，为了获得更好的分类精度，使用训练数据集对HD模型进行多次迭代训练. 在一次迭代中，HD检查所有训练数据点与当前HD模型的相似性. 如果模型错误地对数据Q进行了分类，HD模型则需要对模型进行一定的调整：

    首先，在关联搜索的第二阶段，将查询超向量添加到其所属的类中，并将其从与之错误匹配的类超向量中去除，其数学公式可以定义为

    式中：CiT表示超向量Q的真实类别，CiF表示超向量Q被错误分类的类别，$\hat{\boldsymbol{C}}_i^T$和$\hat{\boldsymbol{C}}_i^F$分别表示模型调整后的真实类别和错误类别.

    其次，类似地，在关联搜索的第一阶段，将查询超向量添加到其所属的超向量组中，并将其从与之错误匹配的超向量组中去除，其数学公式可以定义为

    式中：Cjgroup，T表示CiT所在的超向量组，Cjgroup，F表示CiF所在的超向量组，$\hat{\boldsymbol{C}}_j^{\text {group }, T}$和$\hat{\boldsymbol{C}}_j^{\text {group }, F}$分别表示模型调整后的正确超向量组和错误超向量组. 模型调整需要进行多次迭代，直到HD计算的精度满足条件为止.

3.   实验与结果分析

  • 本文在UCI-HAR行动识别数据集[13]上验证所提模型的有效性，使用准确度、能耗和计算时间作为评估指标，并将测试结果与压缩HD计算(compression HD computing，CompHD)[9]和基于阈值的动态HD计算(threshold-based dynamic HD computing，TD-HDC)[14]等方法进行对比. 其中，CompHD模型利用高维空间的数学知识将超向量压缩为较短的向量，同时保持了全长超向量的信息，从而有效降低模型尺寸，提高模型效率. TD-HDC模型通过设置合适的阈值来保证输入数据被动态地分配二进制和整数HD模型计算资源，实现精度和能耗的有效平衡.

    实验参数设置为：HD空间的尺寸d=10 000，量化参数l=10，分组数量n=1，2，3，4，所有HD计算模型的性能都达到饱和. 连续项内存CiM在HD计算中作为函数实际值的查找表. 建立CiM的过程首先需找到每个特征的最大值Vmax和最小值Vmin；然后，将Vmax和Vmin之间的范围量化为l个层次.

    所有实验均进行了50次独立运行，以获得平均模拟结果. 为了降低硬件成本，映射和编码模块在所有任务之间共享. 所有特征分量都是连续的，实值的，并且缩放到[-1, 1]的范围内. HD计算框架在Python中实现，使用RTL System-Verilog描述推理函数，并使用标准数字ASIC流程来设计专用硬件. 此外，使用ModelSim提取设计切换活动，使用Synopsys PrimeTime测量HD模型的功耗. 所有实验的运行环境为Windows 10系统，AMD Core TR-2950X处理器，128 GB内存.

    • 3.1.   数据集

  • UCI-HAR数据集是根据8位受试者在5 min内以自己的风格进行19种不同活动的记录建立的. 使用来自5个传感器单元的运动传感器数据，每个单元包含9个传感器，根据以50 Hz恒定速率捕获的3轴线性加速度和3轴角速度检测人类活动. 该数据集包含10 299个样本，每个样本具有561个属性.

    • 3.2.   实验结果分析

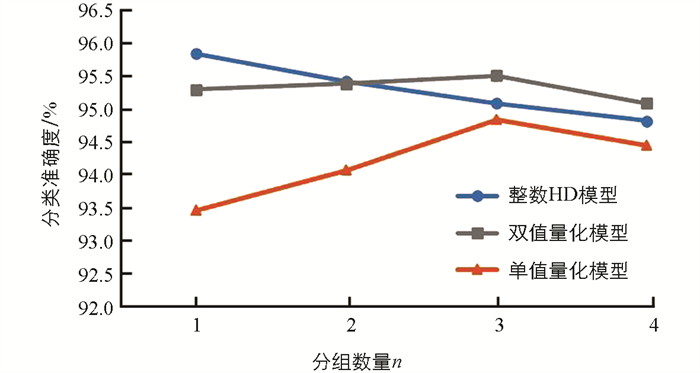
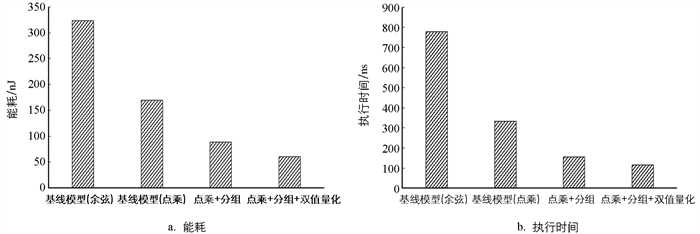
  • 首先，对分组数量n和量化方式进行测试，评估所提方法的有效性. 图 3给出了将类超向量分成$\frac{k}{n}$组、每组包含n个类超向量时的HD分类准确度. 从图 3中可以清楚地看到，分组对标准HD模型的分类准确度存在一定的影响，随着n的增大，分类准确度是逐渐降低的. 但量化技术的引入，可以部分弥补分类准确度，特别是本文设计的双值量化方式，能够在n较大时取得较好的准确度.

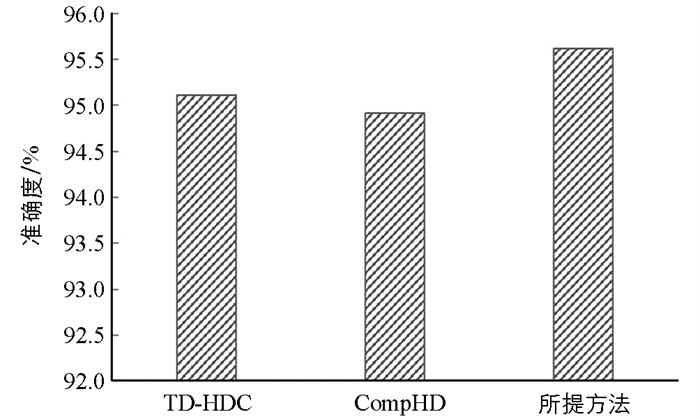
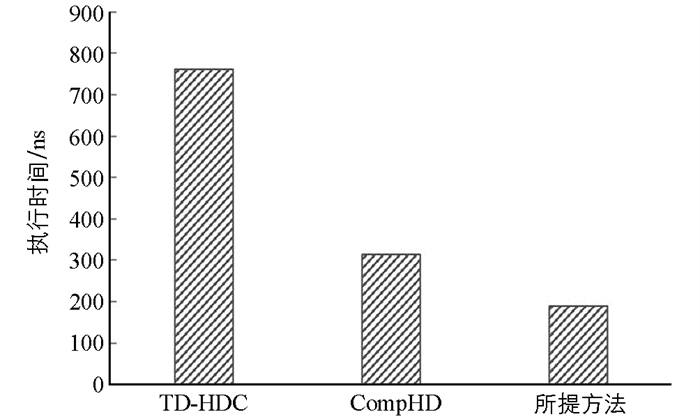
    图 4给出了所提出方法在推理阶段的能量消耗和执行时间. 为了进行公平比较，基线HD使用与本文所提的HD分类方法相同的编码和再训练迭代次数. 从图 4中可以看出，与使用余弦相似度的基线HD计算模型相比，类超向量分组能够明显改善模型的能量效率和计算速度. 这是因为对于一个有k类的应用程序，所提方法减少了推理过程所需的计算数量，即将超向量数量从k个降至$\frac{k}{m}+m$个. 此外，类元素的双值量化技术可以通过去除计算复杂度高的乘法操作来进一步提高模型的效率.

    本文目标是使HD可以在资源有限的嵌入式设备上使用. 为了进一步验证所提方法的优越性，图 5，6给出了本文方法与CompHD，TD-HDC两种方法在分类准确度和执行时间上的对比结果. 从图 5，6中可以看出，本文方法在2个评估指标上均具有优势，从而在保证精度不变的条件下，改善了HD计算模型的计算效率.

4.   结语

  • 本文提出了一种基于分组量化的高效HD计算分类方法，用于解决当前HD计算模型中计算量大、效率低的问题. 实验结果表明，所提模型在保证准确性的情况下降低了计算能耗，可以作为轻量分类器用于小型嵌入式设备上.

参考文献 (14)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回