高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

一种弱监督细粒度深度网络的木材分类方法

,  ,  ,  ,  ,  , 

上一篇

下一篇

戴天虹, 谢千程, 黄建平, 等. 一种弱监督细粒度深度网络的木材分类方法[J]. 西南大学学报（自然科学版）, 2022, 44(10): 161-172. doi: 10.13718/j.cnki.xdzk.2022.10.017
引用本文: 戴天虹, 谢千程, 黄建平, 等. 一种弱监督细粒度深度网络的木材分类方法[J]. 西南大学学报（自然科学版）, 2022, 44(10): 161-172. doi: 10.13718/j.cnki.xdzk.2022.10.017
shu
DAI Tianhong, XIE Qiancheng, HANG Jianping, et al. A Wood Classification Method Based on Weakly Supervised Fine-grained Deep Network[J]. Journal of Southwest University Natural Science Edition, 2022, 44(10): 161-172. doi: 10.13718/j.cnki.xdzk.2022.10.017
Citation: DAI Tianhong, XIE Qiancheng, HANG Jianping, et al. A Wood Classification Method Based on Weakly Supervised Fine-grained Deep Network[J]. Journal of Southwest University Natural Science Edition, 2022, 44(10): 161-172. doi: 10.13718/j.cnki.xdzk.2022.10.017
shu

一种弱监督细粒度深度网络的木材分类方法

  • 1.

    东北林业大学 机电工程学院, 哈尔滨 150040

  • 2.

    无锡科技职业学院 人工智能学院, 江苏 无锡 214000

  • 基金项目: 中央高校基本科研业务费专项资金资助项目(2572019CP17，2572019CP19)；黑龙江省自然科学基金项目(C201414，TD2020C001)；哈尔滨市科技创新人才项目(2014RFXXJ086)
详细信息
    作者简介:

    戴天虹，博士，教授，主要从事图像处理、木材缺陷与检测、无线传感器网络路由协议及汇聚节点选址算法等研究 .

    通讯作者: 李克新，博士，副教授，硕士研究生导师

  • 中图分类号: TP389.1

A Wood Classification Method Based on Weakly Supervised Fine-grained Deep Network

  • 1.

    College of Mechanical and Electrical Engineering, Northeast Forestry University, Harbin 150040, China

  • 2.

    Artificial Intelligence Academy, Wuxi Vocational College of Science and Technology, Wuxi Jiangsu 214000, China

  • 摘要: 针对使用木材的微观结构对木材树种进行识别分类，提出一种新的基于细粒度图像识别的深度卷积神经网络自动分类算法，在阐述Navigator Teacher Scrutinizer Network算法的基础上，首先，利用分段线性激活函数对特征的存在程度和缺失程度的选择能力进行改进，在改进后的特征选择模型算法中搜寻最优α参数；其次，在改进后的算法中加入一个全局K-max池化层并应用在木材分类中，获得最佳的分类结果. 实验结果表明，相比于原始NTS神经网络，本文所提算法能够更准确地实现数据分类，该模型的实验准确率为88.36%，准确率高，实用性强，可以提高木材树种分类精度，为木材树种快速分类提供参考.
    Abstract: Aiming at the identification and classification of the species of wood with the microstructure of wood, a new automatic classification algorithm of deep convolutional neural network based on fine-grained image recognition was proposed. On the basis of elaborating the Navigator Teacher Scrutinizer Network algorithm, the piecewise linear activation function was adopted firstly to improve the selection ability of the existence and lack degrees of the feature, and optimal parameters were searched in the improved feature selection model algorithm. Secondly, a global K-max pooling layer was added to the improved algorithm and applied to wood classification and obtained the best classification results. Finally, experimental results showed that the proposed algorithm can achieve more accurate data classification in comparison with original NTS neural network. The experimental accuracy rate of this model was 88.36%. This accuracy rate is high, and with strong practicability. It can improve the accuracy of wood species classification and provide a reference for rapid classification of wood species.
  • 加载中

  • 图 1  木材的3种切面

    下载: 全尺寸图片 幻灯片

    图 2  NTS-Net网络模型描述图(特征由可视化CNN网络Grad-CAM解释得出)

    下载: 全尺寸图片 幻灯片

    图 3  算法原理结构图

    下载: 全尺寸图片 幻灯片

    图 4  函数的激活功能

    下载: 全尺寸图片 幻灯片

    图 5  合适的激活函数所得决策边界(预想)

    下载: 全尺寸图片 幻灯片

    图 6  全局K-max池化层模型概述

    下载: 全尺寸图片 幻灯片

    图 7  样本扩展方法及效果展示

    下载: 全尺寸图片 幻灯片

    图 8  基于改进NTS-Net算法分类流程图

    下载: 全尺寸图片 幻灯片

    图 9  不同斜率下的分类准确率

    下载: 全尺寸图片 幻灯片

    图 10  数据集上K-max池化层上不同K值的准确率

    下载: 全尺寸图片 幻灯片

    图 11  可视化卷积特征图

    下载: 全尺寸图片 幻灯片

    图 12  训练集损失值变化情况图

    下载: 全尺寸图片 幻灯片

    图 13  测试集损失值变化情况

    下载: 全尺寸图片 幻灯片

    图 14  测试集准确率变化情况

    下载: 全尺寸图片 幻灯片

    表 1  激活函数

    函数名 激活功能
    ReLU y(x)=max(x，0)
    LReLU y(x)=max(x，0)+min(0.01x，0)
    分段线性激活函数 y(x)=max(x，0)+min(αx，0)
    下载: 导出CSV

    表 2  卷积神经网络各层级信息

    层 输出形状 参数
    conv1 224×224 $ \begin{gathered} 7 \times 7,64, \mathrm{~s} 2 \\ 3 \times 3, \max \text { pool, s2 } \end{gathered} $
    covn2_x 112×112 $ \left[\begin{array}{cc} 1 \times 1, & 64 \\ 3 \times 3, & 64 \\ 1 \times 1, & 256 \end{array}\right] \times 3$
    covn3_x 56×56 $\left[\begin{array}{ll} 1 \times 1, & 128 \\ 3 \times 3, & 128 \\ 1 \times 1, & 512 \end{array}\right] \times 4 $
    covn4_x 28×28 $ \left[\begin{array}{ll} 1 \times 1, & 256 \\ 3 \times 3, & 256 \\ 1 \times 1, & 1024 \end{array}\right] \times 6$
    covn5_x 14×14 $\left[\begin{array}{l} 1 \times 1, 512 \\ 3 \times 3, 512 \\ 1 \times 1, 2048 \end{array}\right] \times 3 $
    特征图进入导航网络
    下载: 导出CSV

    表 3  分类准确率计算方法

    预测 合计
    1 0
    实际 1 真阳性(TP) 真阴性(TN) 实际总阳性(AP)
    0 假阳性(FP) 假阴性(FN) 实际总阴性(AN)
    合计 预测总阳性(PP) 预测总阴性(PN) TP+FN+FP+TN
    准确率 P=(TP+TN)/(TP+FN+FP+TN)×100%
    下载: 导出CSV

    表 5  测试结果对比

    卷积神经网络 测试集准确率/% 测试时间/s
    Alexnet 57.12 2 350
    Moblienet 61.03 1 962
    Inception v3 70.51 1 414
    Nts-Net 82.57 366
    改进NTS-Net 88.36 366
    下载: 导出CSV
  • [1] RICHTER H, GROSSER D, HEINZ I, et al. IAWA List of Microscopic Features for Softwood Identification[J]. Iawa Journal, 2004, 25: 1-70. doi: 10.1163/22941932-90000349
    [2] SILVA D N, RIDDER M D, BAETENS J M, et al. Automated Classification of Wood Transverse Cross-Section Micro-Imagery from 77 Commercial Central-African Timber Species[J]. Annals of Forest Science, 2017, 74(2): 1-14.
    [3] MALLIK A, TARRÍO-SAAVEDRA J, FRANCISCO-FERNÁNDEZ M, et al. Classification of Wood Micrographs by Image Segmentation[J]. Chemometrics and Intelligent Laboratory Systems, 2011, 107(2): 351-362. doi: 10.1016/j.chemolab.2011.05.005
    [4] CHEN G S, ZHAO P. Wood Cell Recognition using Geodesic Active Contour and Principal Component Analysis[J]. Optik International Journal for Light & Electron Optics, 2013, 124(10): 949-952.
    [5] IORA F, GURAU L, TIMAR M, et al. Image Processing Method as A Supporting Tool for Wood Species Identification[J]. WOOD FIBER, 2013, 45: 303-313.
    [6] 吴啸天. 基于多特征提取和SVM分类器的木材显微识别[J]. 陕西林业科技, 2017(5): 11-14. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-SXLJ201705003.htm
    [7] GEUS A R, SILVA S F, GONTIJO A B, et al. An Analysis of Timber Sections and Deep Learning for Wood Species Classification[J]. Multimedia Tools and Applications, 2020, 79(45/46): 34513-34529.
    [8] 王伟, 吴芳基于注意机制和循环卷积神经网络的细粒度图像分类算法[J]. 西南师范大学学报(自然科学版), 2020, 45(1): 48-56. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-XNZK202001010.htm
    [9] YANG Z, LUO T, WANG D, et al. Learning to Navigate for Fine-grained Classification[J]. ECCV, 2018, 11218: 438-454.
    [10] HORNIK K. Approximation Capabilities of Multilayer Feedforward Networks[J]. Neural Networks, 1991, 4(2): 251-257.
    [11] BASIRAT M, ROTH P. Learning Task-Specific Activation Functions Using Genetic Programming[C] //Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications. February 25-27, 2019. Prague, Czech Republic. SCITEPRESS-Science and Technology Publications, 2019: 533-540.
    [12] 王元东. 基于ResNet模型的图像分类方法及应用研究[D]. 南昌: 华东交通大学, 2019.
    [13] ZHENG H L, FU J L, MEI T, et al. Learning Multi-attention Convolutional Neural Network for Fine-Grained Image Recognition[C] // 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy. IEEE, 2017: 5209-5217.
    [14] KONIUSZ P, YAN F, MIKOLAJCZYK K. Comparison of Mid-Level Feature Coding Approaches and Pooling Strategies in Visual Concept Detection[J]. Computer Vision and Image Understanding(CVIU), 2013, 117(5): 479-492.
    [15] DURAND T, THOME N, CORD M. WELDON: Weakly Supervised Learning of Deep Convolutional Neural Networks[C] // 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE, 2016, 4743-4752.
    [16] 石洪康, 田涯涯, 杨创, 等. 基于卷积神经网络的家蚕幼虫品种智能识别研究[J]. 西南大学学报(自然科学版), 2020, 42(12): 34-45. doi: http://xbgjxt.swu.edu.cn/article/doi/10.13718/j.cnki.xdzk.2020.12.004
  • 加载中
图( 14) 表( 4)
计量
  • 文章访问数:  3835
  • HTML全文浏览数:  3835
  • PDF下载数:  187
  • 施引文献:  0
出版历程
  • 收稿日期:  2021-03-23
  • 刊出日期:  2022-10-20

一种弱监督细粒度深度网络的木材分类方法

    通讯作者: 李克新，博士，副教授，硕士研究生导师
    作者简介: 戴天虹，博士，教授，主要从事图像处理、木材缺陷与检测、无线传感器网络路由协议及汇聚节点选址算法等研究
  • 1. 东北林业大学 机电工程学院, 哈尔滨 150040
  • 2. 无锡科技职业学院 人工智能学院, 江苏 无锡 214000
  • 收稿日期:  2021-03-23
基金项目:  中央高校基本科研业务费专项资金资助项目(2572019CP17，2572019CP19)；黑龙江省自然科学基金项目(C201414，TD2020C001)；哈尔滨市科技创新人才项目(2014RFXXJ086)

摘要: 针对使用木材的微观结构对木材树种进行识别分类，提出一种新的基于细粒度图像识别的深度卷积神经网络自动分类算法，在阐述Navigator Teacher Scrutinizer Network算法的基础上，首先，利用分段线性激活函数对特征的存在程度和缺失程度的选择能力进行改进，在改进后的特征选择模型算法中搜寻最优α参数；其次，在改进后的算法中加入一个全局K-max池化层并应用在木材分类中，获得最佳的分类结果. 实验结果表明，相比于原始NTS神经网络，本文所提算法能够更准确地实现数据分类，该模型的实验准确率为88.36%，准确率高，实用性强，可以提高木材树种分类精度，为木材树种快速分类提供参考.

English Abstract

    全文HTML

  • 开放科学(资源服务)标志码(OSID):

  • 木材是一种坚硬的纤维结构组织，它构成了森林树木的茎和根. 木材物种分类是一个重要的研究领域，可以帮助打击非法采伐、提供木材证书、征收木材税等. 然而，由于木材组成复杂，现有树种多样性高，很难对木材进行正确的分类. 目前木材树种分类识别主要可以分为宏观和微观两种分类方法. 北罗卡莱纳州立大学维护着一个用于硬木鉴定的在线数据库，该数据库使用国际木材解剖学家协会(IAWA)鉴定的硬木显微特征列表[1]来描述5700多种标本的木材，使用这些特征通常可以在属级区分物种，但是，在种级进行鉴定却很困难，并且由于木材生长环境复杂，极易造成颜色、纹理等特征被改变或破坏，使得木材错分率增加. 另一种方法是使用木材的微观结构对木材树种进行识别分类，即根据木材解剖特征(即组成木材的细胞与组织的形态和排列方式)进行分析、检索并做出判断. 尽管宏观上(指用肉眼包括使用放大镜)观察木材判定或区分树种的方法在生产实践上应用价值很大，但准确性较差，所以，具有较高的分类正确率的微观识别方法极具研究价值.

    木材的显微三维结构需要从3个不同的角度以不同的显微镜放大倍数进行观察，如图 1. 首先，观察横截面：沿纵轴切片，观察导管的布局、年轮和轴向薄壁组织的模式、放大后细胞壁的厚度. 其次，观察弦切面：通过平行与主轴且与年轮相切的方向进行切片获得，弦切面主要用于研究木射线. 最后，观察径切面：通过沿半径切割获得，径切面有助于我们了解木射线. 为了确定木材的种类，从3个角度以不同放大倍数观察来分析树种的解剖特征，观察到的特征与来自专家文献或数据库的数据进行比较[2].

    在计算机领域中实现树种归类的方法主要有两种：木材微观细胞结构分类和木材表面的宏观特性分类. 宏观特征识别技术是通过木材的纹理、颜色和光谱等特征来识别. 微观细胞结构识别技术是通过显微镜得到木材的细胞结构图像，然后对得到的图像进行识别分类. 近些年，基于微观的木材自动分类显示出了一定的潜力. Mallik等[3]提出一种基于图像分割的木材显微分类方法，在放大1 500倍扫描电镜显微图像分割得到的一些特征的基础上，通过SVM和神经网络监督分类方法进行木材分类. Chen等[4]提出一种基于测地线活动轮廓和主成分分析的方法进行木材细胞识别，该方法识别精度高，能够有效区分种内细胞形状变化和种间细胞形状变化. 但这些方法却依赖于分割，而分割效果的不同可能导致不同的分类结果. Iora等[5]基于医学显微镜图像处理程序Image J，提出了一种基于图像分析的方法，并将其应用于3件需要修复的家具物品的物种识别中，但实验物种较少，具有局限性. Silva等[2]使用局部向位量化和局部二进制模式提取纹理特征向量，应用线性判别分析和主要成分分析进行降维，最后使用监督分类来预测样本，获得了较高的分类精度，由于其研究方法严格来说属于半自动分类系统，虽然平均分类准确率高，但工作量大，鉴定耗时. 吴啸天[6]利用支持向量机结合图像的图像梯度方向直方图和局部二值模式特征，对小规模的木材细胞图像的识别分类进行了实验，但训练样本较少，可能会导致分类模型训练不足，结果不够准确. Geus等[7]研究了从预先训练的深度神经网络中迁移学习用于木材物种分类的方法，并将其结果与预先设计的特征方法进行比较，结果证明了使用横截面图像分类的准确率优于预先设计的分类准确率. 针对以上问题，本文提出一种基于深度学习神经网络的自动分类技术，用于识别木材横截面显微图像的种类.

    由于各种木材显微图像特征的相似度高，木材自动分类问题属于细粒度图像分类问题，这就要求分类模型能找到更加细微的局部特征以进行更好的分类[8]. 导航—教师—审查网络(Navigator Teacher Scrutinizer Network，NTS-Net)[9]是一种弱监督卷积神经网络，其在经典的CUB-200-2011鸟类数据集上实现了87.5%的识别准确率(在弱监督分类网络中最佳)，但是在木材分类领域还没有此算法的应用，故本研究将基于NTS-Net的弱监督卷积神经网络对木材进行横截面显微图像分类.

1.   NTS-Net算法和激活函数

    1.1.   NTS-Net算法

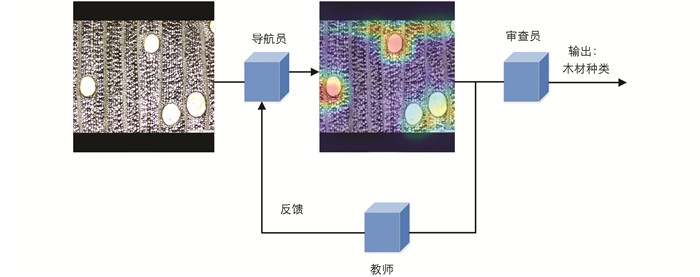
  • 本研究所采用的算法为NTS-Net，该算法专用于细粒度图像识别，模型由3部分组成：一个导航员代理、一个教师代理和一个审查员代理. 该算法设计了一种新的训练范式，使导航员能够在教师的指导下检测出信息量最大的区域，之后审查员仔细检查导航员中建议的区域并进行预测. 该算法在各细粒度图像如飞机和斯坦福汽车等数据集上均展现了良好的计算性能. 图 2为算法模型描述示意图. Navigator为导航员模型，将重点放在信息最丰富的区域(用矩形框表示)，而教师则评估Navigator提出的区域并提供反馈，然后审查员网络仔细检查这些区域以做出预测.

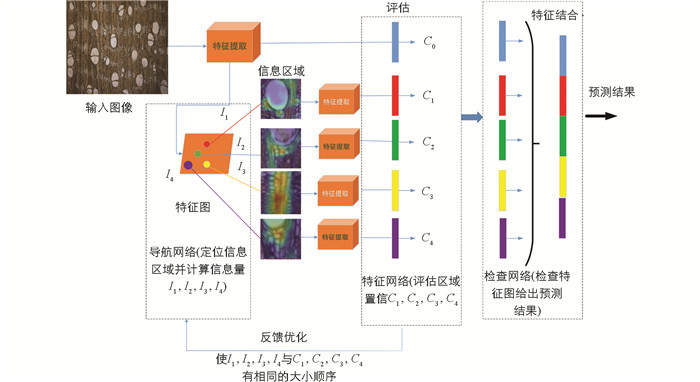
    该算法主体采用残差网络(Resnet-50)基线，Resnet-50是深度为50层的卷积神经网络，网络本身具有先进的特征提取能力，并设计了一个学习排序模块. 网络的主要目标是定位对象(图片)信息最丰富的区域. 假设所有区域都是矩形，将A表示为给定图像中所有区域的集合. 定义了计算区域R和A的信息量的信息函数I，并定义了置信函数C作为分类器来评估该区域R属于标注真值类的置信度，信息量较大的区域应具有较高的置信度，因此应满足以下条件：

    该网络使用导航员网络来近似信息函数I，教师网络近似置信度函数C. 为了简单起见，在区域空间A中选择M个区域，对于每个区域AM，导航员网络评估其信息量I(RI)，教师网络评估其置信度C(RI). 为满足条件，本文采用优化Navigator network以使得信息量{I(R1)，I(R2)，…，I(RM)}和置信度{C(R1)，C(R2)，…，C(RM)}具有同样的顺序.

    综上所述，该网络将Navigator网络预测的M个信息最丰富的区域表示为R={(R1)，(R2)，…，(RM)}，区域的信息量为I={(I1)，(I2)，…，(IM)}，并由教师网络预测其置信度为C={(C1)，(C2)，…，(CM)}. 算法最核心的思想便是使置信度C与信息量I具有相同的顺序从而优化信息区域，如图 3所示. 以下为导航员损失和教师损失函数.

    导航损失函数：

    教师损失函数：

    其中f函数是非增加函数，如果Cs＞Ci，则鼓励Is＞Ii. 导航损失函数惩罚I和C之间的反向对，并鼓励I和C处于相同的顺序.

    当导航员网络导航到信息最丰富的区域{(R1)，(R2)，…，(RK)}时，审查网络产生细粒度识别结果P=S{X，(R1)，(R2)，…，(RK)}，最后使用交叉熵损失作为分类损失：

    • 1.2.   激活函数

  • 从简单的阈值函数开始，最初开发激活函数时的重点是逼近函数，如Sigmoid和Tanh. 万能逼近定理[10]中所述，若激活函数是连续、有界且单调递增的，则任何连续实值函数都可以由具有一个隐层的前馈网络很好地逼近，然而，当网络越来越深时，这类函数都存在梯度消失的问题.

    为了克服这个问题，人们引入了各种非逼近函数，其中ReLU函数为深度学习的成功奠定了基础，当ReLU的正输入导数为1时，梯度不会消失，同时，所有的负值都会被映射到零，由此会产生两个问题：

    1) 存在没有负值的信息流，也就是所谓的“死亡ReLU”；

    2) 激活值的统计平均值将会大于零，所有负值都被同等对待.

    表 1为目前广泛使用的激活函数.

2.   改进NTS-Net网络的木材物种分类方法

  • 为了更有效地捕捉相似的类之间微小细微的差异，我们提出一种改进的NTS-Net算法，以适合复杂的细粒度图像分类任务.

    • 2.1.   分段线性激活函数

  • 在神经网络中，单个神经元j的输出aj由下式计算：

    其中a是n个相连神经元(来自前一层)的输出，ωi，j是相关权重，f(x)称为激活函数的非线性函数. 在f(x)的编码输入中，某个特征存在或不存在的状态表示为：如果f(x)＞0，则该特征存在，如果f(x)≤0，则该特征不存在.

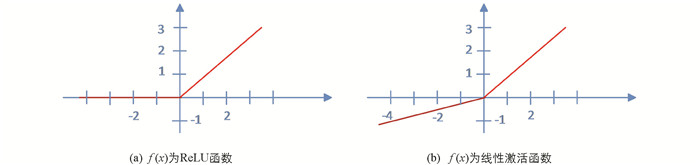
    对于现有的大多数激活函数来说，其存在度的定义有很多且表现良好. 图 4表示了表 1所示目前广泛使用的激活函数.

    在ReLU函数的情况下，通过函数的正部分(即x＞0)实现的，但却不能够很好地捕捉特征缺失程度. 例如，ReLU函数定义了一个明确的“关断状态”或“去激活状态”，即对于所有负值，f(x)=0，通过这种方式，神经元不会模拟任何可以传播到下一层的缺失程度信息. 对于包括粗粒度视觉分类在内的许多应用来说，只考虑存在的特征. 然而，对于细粒度视觉分类来说，仅仅对存在的特征进行建模是不够的，在细粒度视觉分类中，不同的类通常具有相似的外观，并且通常在细微的视觉差异上有所不同.

    由于特征的存在，缺失程度与R的正域和负域有关，我们采取分段函数对正值x＞0和负值x≤0进行建模，如式(6)：

    其中α≥0定义了负部分线性函数的斜率. 对α参数设置为：α=0.01，便得到了LReLU激活函数. 实验表明，这种小斜率对于粗粒度视觉分类来说效果显著，对于细粒度视觉分类来说表现不佳，主要因其缺少特征的存在缺失程度，不能够准确地建模分类. 公式(6)同样适用于随机选择斜率的RReLU函数，至于PReLU函数，其斜率参数是依据数据估计的，因为优化器经常陷入局部极小值，所以该函数在实践中不够灵活，推广较难.

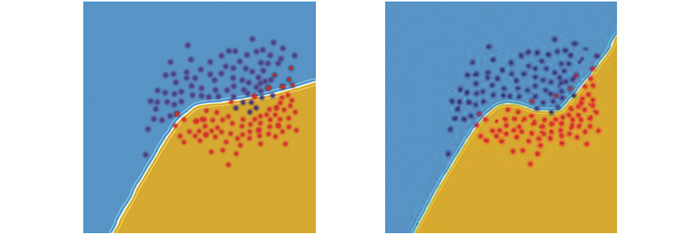
    从以上分析可知，参数α的合理设置是解决特征存在、缺失程度问题的关键所在. 根据文献[11]可知，不同的问题没有唯一的解决方案. 文献[11]还表明，对于不同复杂性的分类任务，不同的激活函数计算效果显著，不同的数据集可能具有不同的可分性，需要学习具有不同属性的激活函数，可根据选择合适的斜率(参数α)来实现，如图 5所示.

    • 2.2.   全局最大池化层

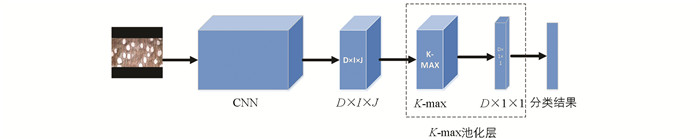
  • 通常在Resnet-50的最后一个卷积层和分类层之间使用全局平均池化层(GAP)[12]，这些池化操作允许分解最终卷积层的空间维度并获得描述图像的单个向量. 对于细粒度视觉分类而言，已表明基于部分的方法(例如文献[13])可以提高分类性能. 为此，本文使用全局K-max池化层(GKMP)[14]，使得NTS-Net网络可以在图像最重要的K个激活特征进行学习(在反向传播期间，误差通过K个最重要的部分进行传播，不同于全局最大池化层的一个部分，也不同于全局平均池化层的全部)，其可视为一种简单的注意力机制.

    如图 6所示，全局K-max池化层定义如下：给定一个输入图像x，设y∈RD×I×J为Resnet-50最后一个卷积层的输出，其中y的空间分辨率为I×J(在本文中为14×14)，包含D个特征映射. 此外，给定一个特定的d∈{1，…，D}，其排序向量Sd包含以降序排序的yd值：

    然后，针对指定K的全局K-max池化操作可定义为

    该定义源于文献[15]中所使用的池化操作，但其中还包括K个最小激活定义，而本文实验表明，当包括最小激活时，此定义不会有助于识别性能的改善. 因此，我们使用式(8)中定义的全局K-max池，若选择K=1，则式(8)为标准全局最大池化层，若选择K=i×j，则为全局平均池化层，本文选取K=4进行最优试验.

    • 2.3.   数据预处理

    2.3.1.   数据获取

  • 本研究针对中非70种商业木材的横截面显微图像[2]进行木材分类，木材显微图像数据库由25科58属77种刚果木材的1 221张图片组成. 根据这份清单，在光学显微镜下检查了中非皇家博物馆(Tervuren Xylarium)所有可用解剖切片的横截面显微图像，仅选择无裂纹和伪影(如封闭气泡)、质地均匀、足够薄且无染色剂的切片，横切面用滑动切片机切割，分级乙醇系列(50%，75%，96%和100%)脱水，并用优巴拉尔(Euparal)固定.

    • 2.3.2.   数据增强

  • 深度学习是一种标准的数据驱动模型方法，深度网络作为黑箱依赖于大量数据解决问题，本研究中采集的数据集数量略小，所以本文对实验的数据集进行了扩展.

    分类网络的数据集扩展的方法通常有平移旋转等仿射变换法、镜像法、弹性形变法等，本研究中利用旋转、加噪声等方法对数据集进行扩展，将实验数据集扩展为10倍，共计12 210张，图 7是数据增强方法和效果展示.

    • 2.3.3.   环境搭建及参数设置

  • 本研究中分类精度为种级，对于样本的标注，根据数据集原本种属标签逐一进行标注，确保样本标签的准确性.

    实验在搭建的深度学习工作站中进行，系统环境为ubuntu14.04，使用的深度学习框架为pytorch，并且使用CUDA工具包建立开发环境，利用GPU加速深度学习，使用的GPU型号为NVIDIA TITAN XP，显存为24G. 实验中，预先处理图像大小为448×448. 算法使用完全卷积网络ResNet-50作为特征提取器，并使用批量标准化作为正则化器. 算法使用Momentum SGD作为优化方法，学习率设置为0.001，模型训练共用时4 h.

    • 2.4.   基于NTS-Net网络的木材物种分类模型

    2.4.1.   卷积神经网络模型参数

  • 改进的卷积神经网络算法各层级信息如表 2所示，我们使用全卷积网络作为特征提取器，没有全连接层. 具体来说，卷积层逐层计算特征层次，经过分段线性激活函数和K-max池化，得到一系列不同分辨率的特征图.

    输入448×448尺寸的图像，经过第一个7×7大小，s=2的卷积核卷积运算，再由3×3窗口，s=2的池化层降采样操作，输出224×224尺寸的特征图；之后的4个组块(各组块中各有3个bottleneck残差结构)共12个bottleneck残差结构的计算，输出特征图缩小到14×14. 再将特征图输入导航网络. 由表 2可以看到随着特征提取过程的进行，特征图的尺寸不断减小，算法逐步提取出更多且更高级的图像特征信息，以更好地胜任分类识别任务.

    • 2.4.2.   基于NTS-Net网络的木材识别流程

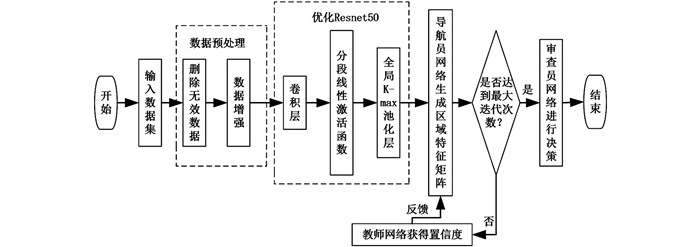
  • 基于以上构建的改进NTS-Net工作流程如图 8所示，主要包含以下几部分：图像数据输入预处理模块、卷积网络特征模块和NTS-Net弱监督网络分类模块.

    输入数据预处理模块：对原始图像数据进行预处理的操作主要包括删除掉模糊重复的无效数据，对图像进行加噪、旋转等操作，以扩充图像数据，并将木材图像增强后的共12210张木材显微图像按训练集和测试集8∶2的比例划分，输入卷积网络；卷积网络特征提取模块：将输入图像数据，分别输入到构建的基于优化ResNet50模型进行特征提取；NTS网络分类模块：导航网络将模型导航到信息最丰富的特征区域，而教师网络评估建议的区域提供反馈，之后，审查网络审查这些区域以做出预测.

3.   实验结果分析

  • 为了验证本文所提算法的分类性能，我们在木材横截面显微图像数据集上进行以下实验，80%的样本用于训练，20%的样本用于测试. 准确率(P)计算方式如表 3所示[16].

    1) 在原始NTS算法上进行改进ReLU函数算法试验，验证当测试10种木材样本时最适合分段线性激活函数斜率α的值；

    2) 在最优斜率α的改进算法上，在Resnet中加入全局K-max池化层，测试10种木材样本下，K分别等于1，2，4，8，16，32，196时算法的准确率.

    3) 改进的NTS-Net与其他网络分类准确率的实验对比.

    • 3.1.   ReLU函数斜率α实验

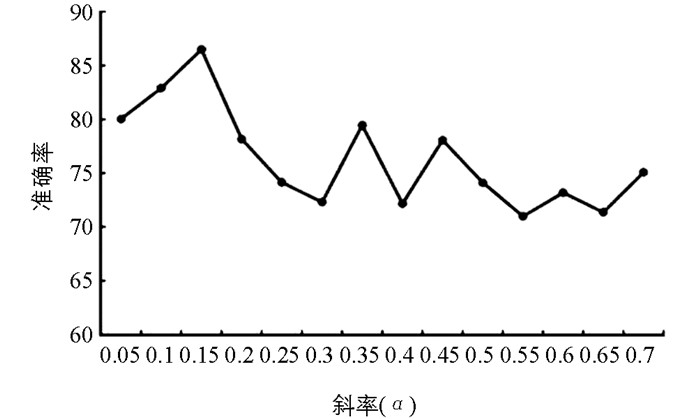
  • 基于不同斜率α的测试函数实验测试结果如图 9所示. 由仿真实验数据可知：该算法具有良好的收敛效果与较高的求解精度，即增加斜率会降低算法的分类精度. 然而，实验证明0.05至0.2范围内的轻微斜率(峰值在0.15)与原始算法相比较，明显优于ReLU函数，由此得出结论，由于细粒度视觉分类种类间更加相似，任务更加复杂，因此，模拟特征缺失程度变得越来越重要.

    • 3.2.   全局K-max池化层实验

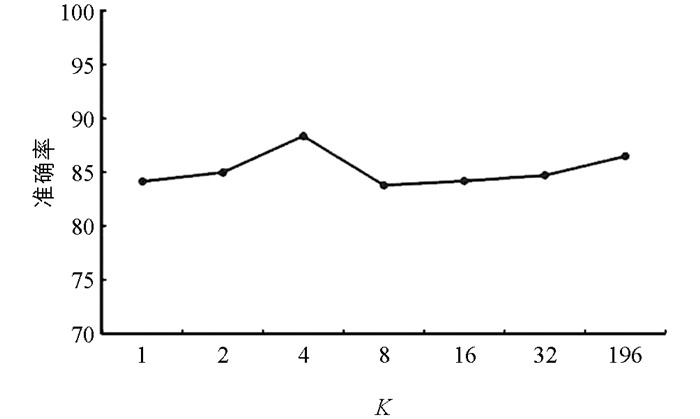
  • 图 10显示了在全局K-max池化层选择不同K值的效果，特别当K=1时，相当于全局最大池化层. 我们可以观察到，K=4左右的值似乎是最佳的，与原始算法相比，改进了1.07%的绝对值.

    此外，为更好地分析本文网络获得图像特征表达的过程，分别将各模块中卷积层的输出特征图可视化，如图 11所示，可以看出随着网络层数的提高，所提取的图像特征越来越抽象，特征的纹理性逐渐被更高级的语义性所取代. 而本文提出的网络从过程上看获得了较为丰富的边缘信息，从结果上看又取得了较高的识别精度，适用于木材显微图像的识别.

    • 3.3.   改进的NTS-Net与其他网络分类准确率的实验对比

  • 作为比较，本研究还与Alexnet，Inception v3，Mobilenet等经典卷积神经网络进行了木材分类预测对比实验，在对比实验中，3个卷积神经网络均在tensorflow深度学习框架下运行，系统环境与参数设置均与本研究网络NTS-Net相同. 实验结果如表 5所示.

    • 3.4.   改进算法实验结果

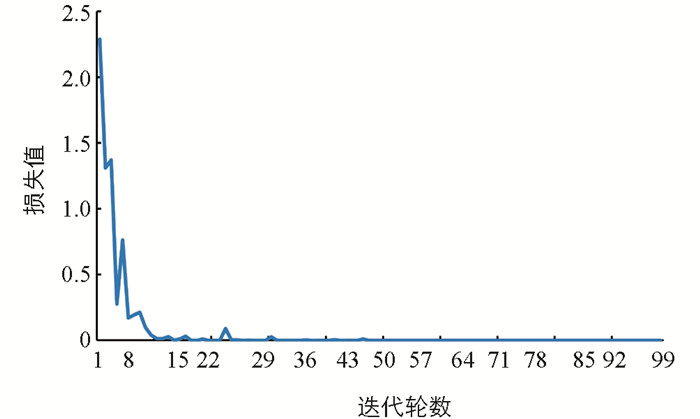
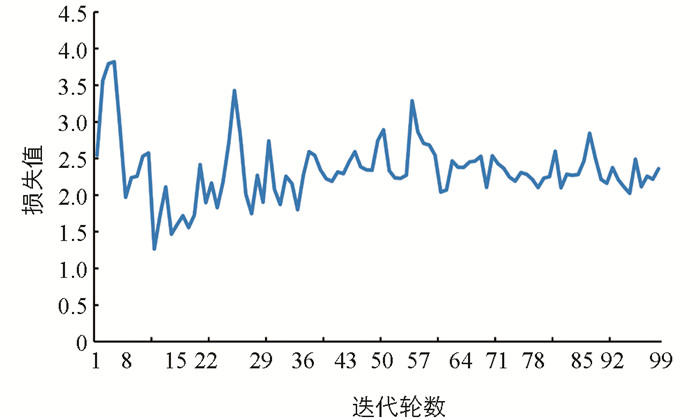
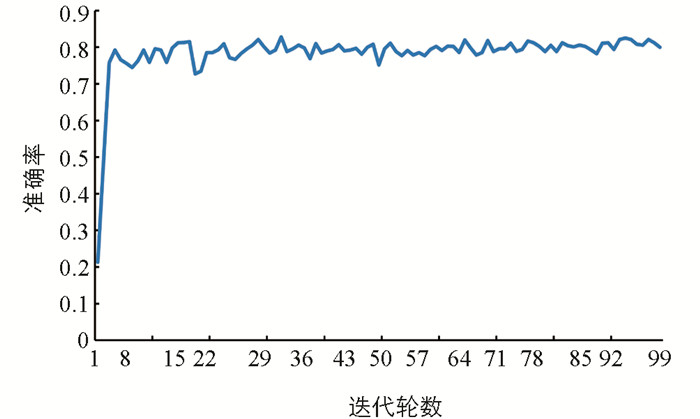
  • 本实验最终达到了88.36%的准确率，这在同类的识别算法中实现了最佳的性能，说明了本网络在NTS-Net中加入分段线性激活函数和全局K-max池化层的有效性. 训练过程中的训练集损失变化情况如图 12所示，测试集损失变化如图 13所示，测试集准确率变化如图 14所示. 从图中可以看出，本文提出的改进算法收敛速度快，识别准确率高，训练集的损失值在11轮左右便下降到接近于0的数值，测试准确率在5轮左右就已经达到80%.

4.   讨论

  • 虽然目前没有公认的标准来比较木材解剖鉴定分类获得的结果，但上述实验的高准确率清楚地说明了本研究算法自动分类的潜力. 对分类准确率最高和最低的木材种类进行分析，狄氏黄胆、黑驼峰楝、西非铁青木3个树种的分类准确率较低，分别为77%，75%，81%，实验准确率较低的原因可能是这些物种都有较大的导管、较低的导管密度和较大的木射线. 非洲肉豆蔻和古夷苏木两个物种的分类准确率为100%，或是因为这些物种有特定的导管排列顺序和网状轴向薄壁细胞，最有可能导致分类结果的原因是有无轴向薄壁细胞，这也是本文提出算法的优点，将每个提出的区域扩大到相同大小，再从中提取特征，将区域特征与整幅图像的特征联合处理，进行细粒度分类，信息区域有助于更好地表征物体，因此，将信息区域的特征与全图像融合能获得更好的性能.

    由以上分析可知，应用本文方法仅用木材横截面显微图像就可以区分物种. 但是，非洲肉豆蔻有一些非常特殊的木材解剖特征，在横截面显微图像上没有显现，因此，在后续研究中会将木材弦切面显微图像和径切面显微图像加入到实验中，再分析算法分类的准确性.

5.   结论

  • 本文利用一种基于细粒度图像识别的深度卷积网络的改进算法进行木材分类，该算法自动提取木材显微图像局部特征并结合整个木材横截面显微图像特征进行木材分类. 显微图像经简单处理后实现端到端的木材分类过程，通过多个仿真实验验证了所提方法的性能. 通过与原始NTS-Net算法进行对比，结果表明，在改进ReLU激活函数与加入全局K-max池化层的样本数据中，所提改进算法能够有效提升分类准确率，并且实现端到端的木材分类，算法收敛速度快，评估准确度高，节省了大量的时间. 从应用的角度看，如果将本研究成果应用于木材分类实际操作中，该算法可以快速大量给出分类结果，其分类结果可以作为木材专家进行木材分类的一个参考依据.

参考文献 (16)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回