-
开放科学(资源服务)标志码(OSID):

-
在岩土工程领域,边坡稳定性问题是最基本的问题之一,广泛存在于天然边坡、人工边坡、挡土结构、水库大坝等结构的整体及局部稳定性分析当中,其中,确定边坡潜在滑动面的位置和形状对边坡稳定性分析结果具有决定性和控制性作用[1].
关于边坡危险滑动面的获取与确定问题目前已经开展了广泛的研究,取得了较多的成果,边坡危险滑动面的获取分析理论大致有极限平衡理论、滑移线场理论、极限分析理论、数值分析方法和差分理论等5种方法[2]. 其中以极限平衡法[3]和数值分析方法[4]应用最为广泛. 极限平衡法是通过对边坡内某一给定形状确定的滑面,计算该滑面对应的安全系数,进而搜索边坡不同位置所有可能的滑面,找出安全系数最小的滑面作为潜在最危险滑面[5]. 数值分析方法与强度折减概念相结合在目前也开展了许多研究,包括参数折减模型[6-7]、失稳判据[8]、滑面推算[9]、安全系数[10]、计算精度[11]、各种特殊工况下的应用[12-13]等,已经成为边坡滑移面推算与搜索的主要数值分析手段. 强度折减理论通过逐步折减边坡岩土强度参数取值,最终促使边坡逼近极限平衡状态,极限平衡状态下强度参数折减倍数即为安全系数,此时滑移面可通过相应判据规律确定. 由于基于有限元法或有限差分法的强度折减法不需要提前设定滑动面的位置和形状,从而显著地减少了推算过程中的人工干预,所得滑面结果更加精确. 因此,部分学者采用此类方法进行边坡次级滑动面的搜索与确定,其中包括了赵尚毅等[14]采用最大剪应变增量原则确定边坡滑动面及求解最小安全系数;孙冠华、聂治豹等[15-16]以等效塑性应变为判据计算边坡滑动面. 此外,基于应力影响系数法的边坡滑面确定方法及基于极限应变的判断原则,以能量突变为依据的判定方法等方法也得到了发展. 但有限元强度折减法也存在一些难以避免的不足,如极限平衡状态的判据问题、从塑性区中提取滑面的算法问题、有限元计算中的网格畸变问题等. 由于有限元方法在模拟计算大变形区域过程中会产生数值不稳定性,从初始状态到后续大变形的整个变形过程难以连续求解,因此,计算流体动力学(CFD)建模和离散建模(如DEM)等方法逐渐发展了起来. 而CFD计算要求材料是特殊类型的流体[17],难以解决静态变形问题,DEM离散建模也不适合处理基于连续介质近似的土体本构模型[18].
综上所述,确定土坡滑面位置的演化,进而分析土坡的稳定性与动态滑动,是目前传统的极限平衡法和有限元方法难以解决的问题,然而这个过程的求解显然十分重要,整个变形过程中包含了许多信息(如破坏区、滑面演化、破坏过程、破坏时间、推移距离、冲击力等). 因此,以土坡从小变形到大变形连续求解整个变形过程的视角出发,探究土坡滑面的位置和演化过程具有重要意义.
无网格法作为求解整个变形过程的一种方法,是一种有潜力、有效的大变形求解方法. SPH方法属于拉格朗日方法,可以解决大变形问题而不产生网格畸变,在岩土工程问题中有较好的发展潜力. 此外,由于SPH方法基于连续介质近似,能够较好地表达控制方程和现有岩土材料的本构模型,进而求解岩土材料的整个变形过程. 目前SPH方法已被用于解决许多相关岩土问题并取得了一些显著的成果[19-22],但目前的研究中尚缺少基于SPH从整个变形过程的视角出发,确定土坡的滑面位置的相关研究.
基于土体理想弹塑性本构模型,根据最大剪切应变率原则选取最大剪切应变率SPH粒子,多组最大剪切应变率粒子贯通可确定滑面位置与形态. 文中采用了Fortran编程进行SPH理论计算与滑面确定,所确定的滑面与极限平衡法确定滑面进行了比较,并分析了土坡稳定性与土坡形变间的关系,此方法为土坡滑面的确定与分析提供了一种新的方式.
全文HTML
-
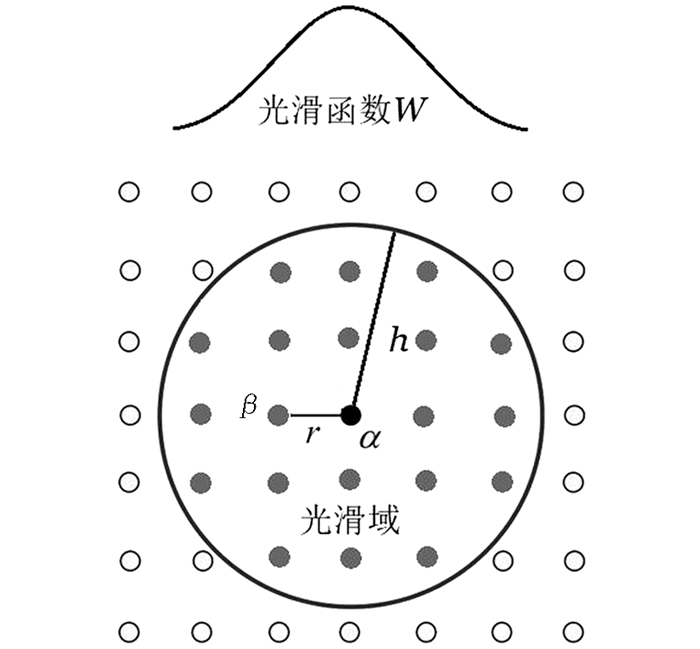
在SPH方法中,计算对象用一系列粒子的集合表示. 一方面,粒子的运动可以单独求解;另一方面,SPH方法通过采用了独特的插值理论,将一系列粒子结合起来以表示连续介质的变形. 上述插值理论包括两个关键步骤:核近似和粒子近似. 使用核近似法,对于参考粒子α,基于支持域内的相邻粒子β,引用光滑函数W插值计算,如图 1所示,h是光滑域半径,影响域半径的h由粒子间的初始距离r乘以参数kd得到。
核近似场函数表示为[23]
光滑函数W用来表示临近的β粒子对α粒子的影响. 本文中三次样条函数取为光滑函数[24].
其中,R=|x-x′|/h,在二维和三维空间,αd分别取15/(7πh2)和2πh3.
另外,粒子近似将粒子的信息用光滑域内的其他粒子表示,其特征如下:
其中Wij=W(xi-xj,h),m和ρ分别表示粒子的质量和密度.
-
本文中使用的控制方程是基于固体力学的方法,连续性方程和运动方程可以表示为
其中ui是速度矢量,ρ是密度,σij是应力张量和Fi是外力向量. 将SPH插值理论应用于状态方程,上式可以写为
其中Cij为人工黏性项与人工应力项,表示为
式中δij是克罗内克δ函数,
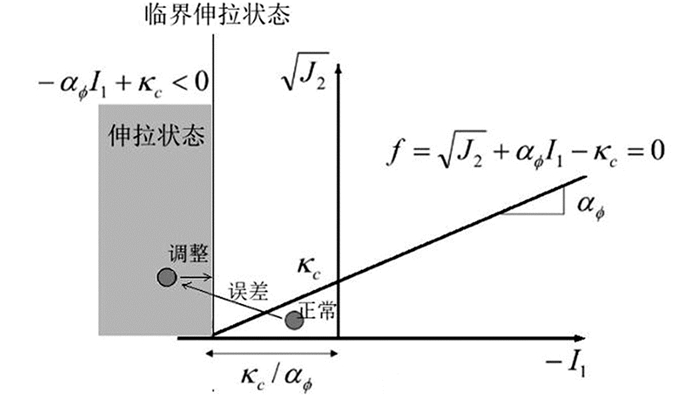
$\prod\limits_i$ 是人工黏性,Rijα和Rijβ是人工应力张量,fαβ是排斥力项,nAS是常数,可设置为4. 人工黏性项与人工应力项是为了解决SPH算法中数值不稳定性问题,拉伸不稳定性,尤其是张拉变形计算的不稳定性,是固体力学SPH方法主要存在的问题之一.本文研究中将岩土体假设为理想弹塑性材料,采用Drucker-Prager屈服准确定岩土体的塑性流动状态,其抗剪强度使用黏聚力和内摩擦角来表示. 当岩土体的应力状态处于塑性屈服状态时,它随屈服函数的变化而变化. 然而,数值误差会导致应力状态超过屈服函数. 因此,模拟计算过程中需要及时纠正计算粒子的应力状态,本文采用Chen等[25]提出的应力映射调整算法. 图 2为拉伸开裂处理示意图. 如果计算粒子的应力状态在计算中出现误差,处在了拉伸状态,即对应式(9)条件,将静水压力应力分量进行调整,修正到临界拉伸状态.
式(9)中σijn和σij′分别为应力拉伸状态处理调整前后的粒子应力张量.
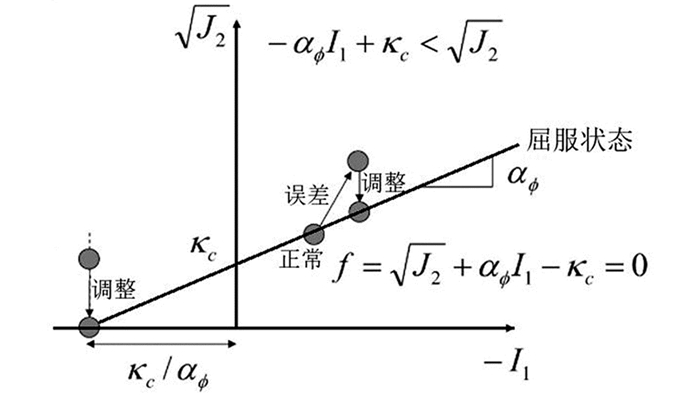
图 3表明了在计算模拟过程中出现计算误差、粒子应力状态超出了屈服表面、采取应力调整的过程. 按比例系数R减小偏切应力分量,静水应力分量I1保持不变,如式(10)所示.
其中σij′是经粒子伸拉状态处理后的粒子应力张量;R是调整比例系数,由式(11)计算.
除了上述应力调整之外,本文还采用了Jaumann应力速率来考虑刚体自旋运动的影响.
-
在边坡稳定性分析中(极限平衡法),安全系数通常定义为抗滑力与下滑力的比值,因此,以弹塑性岩土体为例,极限平衡临界状态意味着滑面上岩土体均处于塑性屈服状态. 与基于有限元法或有限差分法的强度折减法相似,基于SPH的边坡稳定性分析的强度折减法通过对整个土坡的岩土体抗剪强度参数c和φ进行一系列折减得到ct和φt,如式(12)和式(13)所示.
上式中c和φ为岩土体实际抗剪强度参数;ct为强度折减后的黏聚力值;φt为强度折减后内摩擦角值;FOSt为试算的安全系数(折减倍数). 一般初始时刻FOSt设置得足够小,以便系统稳定. 随后,FOSt值逐渐增加,直到出现贯穿的滑面并持续呈现,边坡失稳,使边坡出现临界失稳状态的FOSt的最终值被定义为边坡的安全系数.
基于有限元法或有限差分法的强度折减法在确定边坡的极限平衡状态时有多种判别标准,如计算收敛、塑性区贯通、最大位移等[26]. 与此不同的是基于SPH的强度折减法在模拟计算过程中,可以连续求解从小应变到大变形的整个变形过程,而且可以求解破坏区、破坏时间、移动距离等.
-
应用强度折减法确定滑动面的形态计算时,确定极限平衡状态与判定滑动面位置是其中的关键. 从连续求解由小应变到大变形的整个变形过程的视角出发,不同于有限元方法,SPH框架下土坡在整个变形过程中确定极限平衡状态临界点的意义不大,因为土坡变形的计算过程必定会趋于收敛,故采用SPH方法重要的一步是判断滑动面位置.
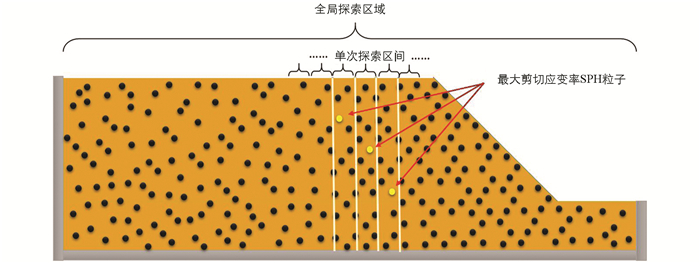
当土体承受的剪切力达到最大抗剪强度后,随着土体的连续变形,土体抗剪强度便降到残余强度,本文的研究假设不考虑滑面上岩土体材料塑性屈服后剪切强度的减弱,也就是说,切面残余剪切强度仍等于峰值剪切强度. 在判断土坡滑面位置的分析中,时间间隔Δt内,每个滑面搜索区间内最大剪切应变率的粒子发生的剪切位移是最大的,因此,粒子最大剪切应变率可以作为土坡中滑动面判定的标准. 具体而言,若任一土坡其稳定性不足,即会发生变形,进而失稳滑动. 在土体滑动发生的过程中,首先在全局搜索区域(土坡全长或滑面可能出现范围)中划分单次搜索区间,单次搜索区间的最优长度是1.1~1.2倍初始粒子间距,即S=(1.1~1.2)d,根据单次搜索区间的最大剪切应变率原则选取最大剪切应变率SPH粒子,在土坡滑动进行的某一时刻开始,多组最大剪切应变率粒子会形成贯通,即确定了土坡的滑面位置与形态,如图 4所示.
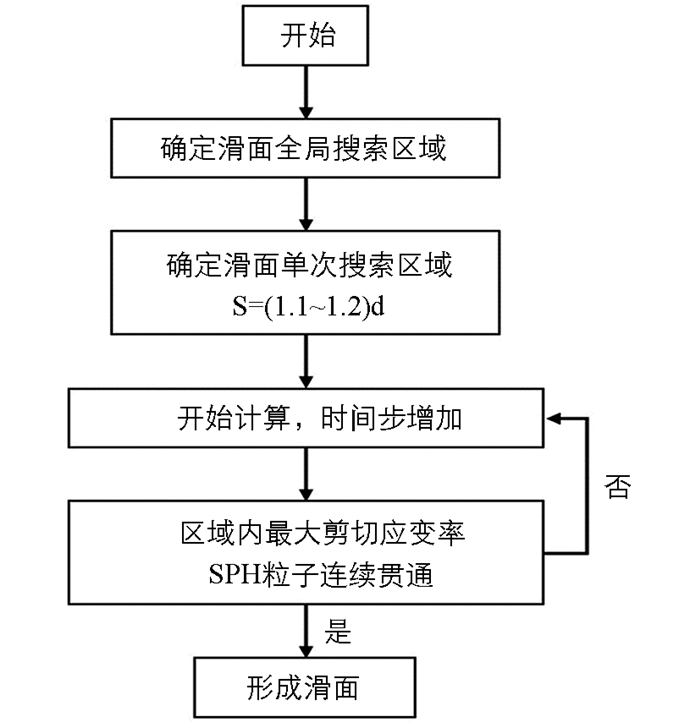
上述SPH方法的土坡滑面确定流程图如图 5所示,依次确定滑面全局搜索区域、单次搜索区域、开始计算和时间步增加,直至某一时刻下多组最大剪切应变率粒子形成贯通,即确定出土坡滑面. 值得注意的是:(1) 当土坡强度参数足够保持稳定时,显然土坡处于稳定状态,此时通过SPH方法进行土坡模拟计算,土坡不会发生变形与运动,因而不会形成滑面,若引入强度折减法降低土坡强度参数,某一状态下土坡会开始变形与运动,此时才能形成滑面;(2) 某一状态下土坡会开始变形与运动,当多组最大剪切应变率粒子形成贯通后,随着土坡运动的发展,不同时刻下最大剪切应变率粒子贯通的滑面并不一致,他们是位置相互靠近且十分接近,这表明某一状态下的土坡运动过程中滑面位置并非丝毫不变,而是有一定变化,并且滑面位置均十分靠近而形成“滑带”,这与土坡失稳运动后的实际情况是一致的.
1.1. SPH的基本理论
1.2. 固体力学的SPH方法
1.3. 基于SPH的强度折减方法
1.4. 滑面分析方法
-
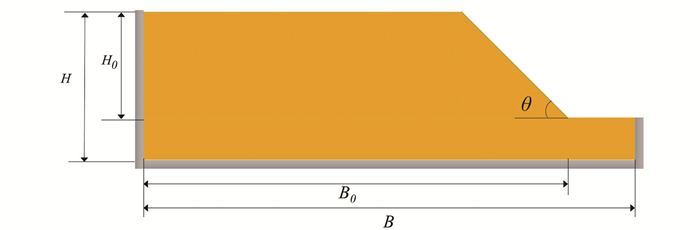
基于弹塑性本构的土体SPH模型精度在前期的研究中已经得到验证[27],在这个算例中,为了满足经典瑞典条分法的分析条件,计算中将剩余强度设置为峰值强度. 图 6是数值算例的尺寸示意图,边坡由均质土体构成,为了尽量消除竖直边界条件对模拟结果的影响,模型加大了底面尺寸建立了如图形状简单的模型. 模型左侧是90°垂直边界,右侧是坡角45°的斜坡,表 1列出了本次模拟使用的参数. 模拟使用了Drucker-Prager屈服准则,模型底部的边界采取了无滑移边界处理,模拟考虑了Jaumann应力速率,没有考虑孔隙水压力的影响,在静止土压力的基础上对边坡进行重力加载.
根据前述模型尺寸与参数建模计算,在初始强度参数(c=12.31 kPa,φ=31.30°)下,计算结果中模型随时间推移并没有发生明显的形变,说明边坡处于稳定状态. 按照强度折减的理念,逐渐增加折减系数依次进行计算,当折减倍数为0.85时,土坡开始在重力作用下发生失稳破坏、滑动. 图 7-图 11中横坐标与纵坐标均表示模型尺寸.
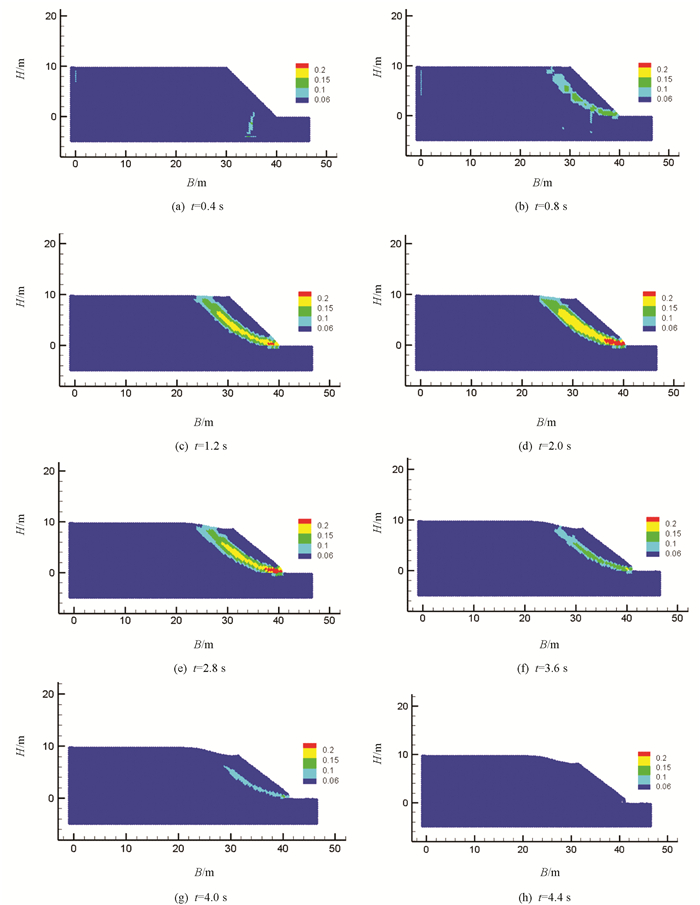
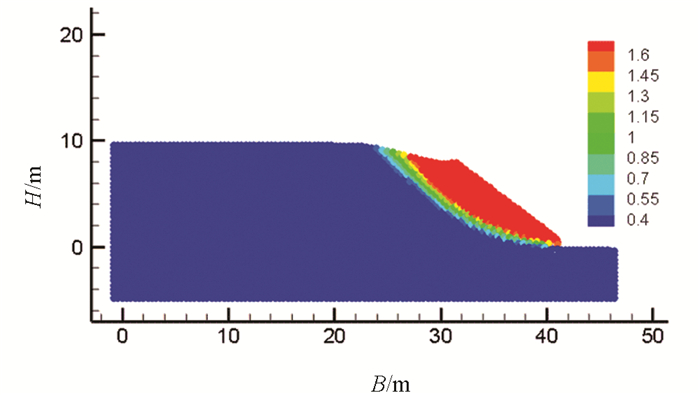
图 7展示了算例在SPH框架下从小变形到大变形连续求解的过程,显示了土坡SPH粒子在不同时刻的瞬时剪切应变率分布,图 7(a)-7(b)可见土坡的剪切应变率逐渐增大,分布由分散状态逐渐聚集为条状,但土体塑性屈服区尚未贯穿;图 7(c)-7(e)土坡变形速率增大,剪切应变率继续增大到最大值,形成贯穿的塑性屈服区,即塑性剪切带;图 7(f)-7(g)中土坡变形速率逐渐减小,剪切应变率也逐渐减小,部分剪切区瞬时剪切应变率降低为零;图 7(h)中时间到4.4 s以后土坡运动停止,瞬时剪切应变率均为零.
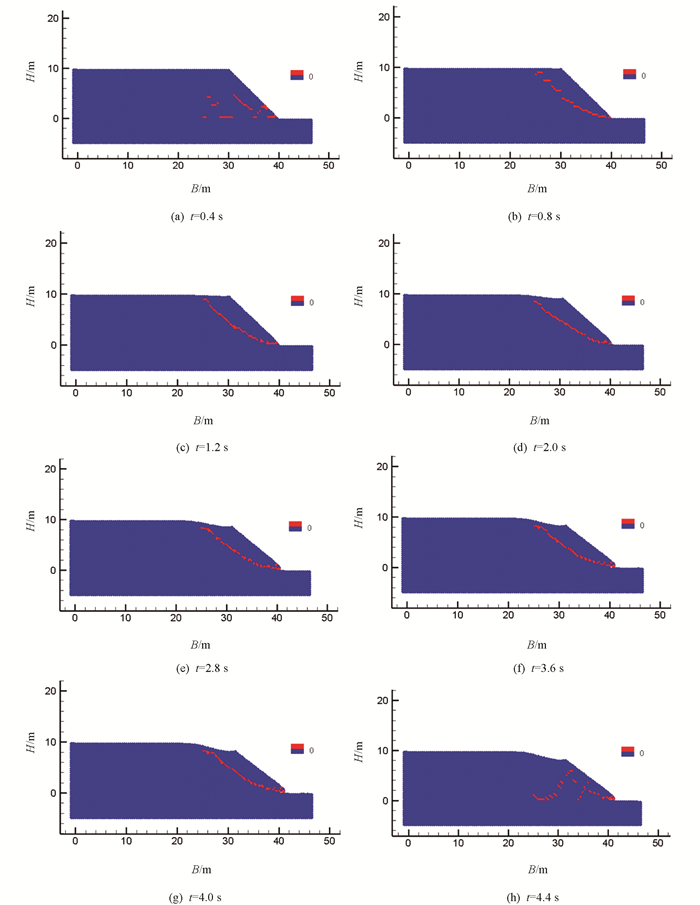
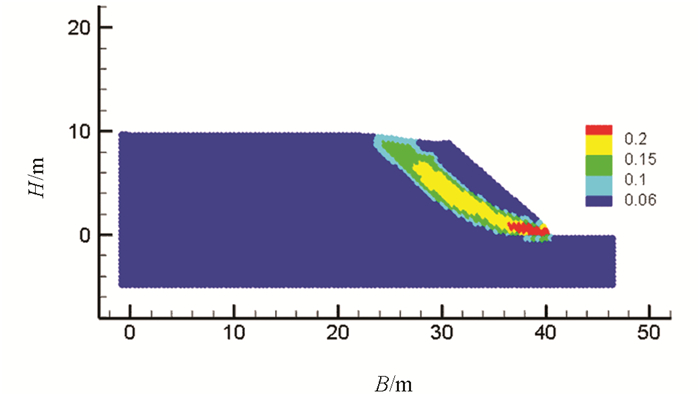
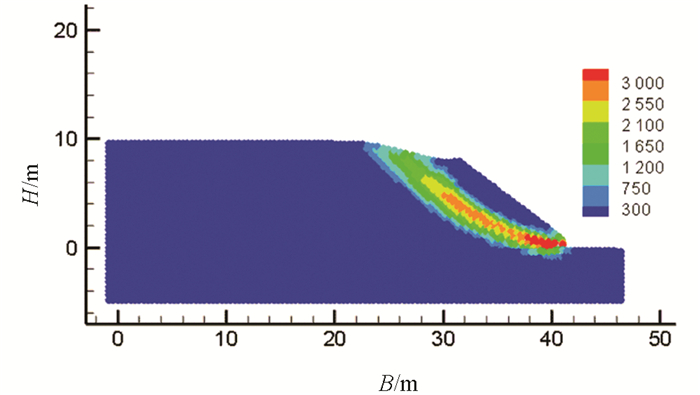
图 8显示了与图 7相对应时刻滑面判定的最大剪切应变率SPH粒子位置的分布,图 8(a)-8(b)可见滑面尚未贯穿,图 8(c)-8(g)显示土坡运动过程中可确定其滑面,图 8(g)可见土坡运动停止后,最大剪切应变率SPH粒子位置分布呈无序状态. 图 9提取了计算过程中最大剪切应变率出现的时间(1.7 s),此时最大剪切应变率值为0.298 0,图 10与图 11分别显示了算例中滑坡变形运动终止时的位移分布与累计塑性应变分布.
-
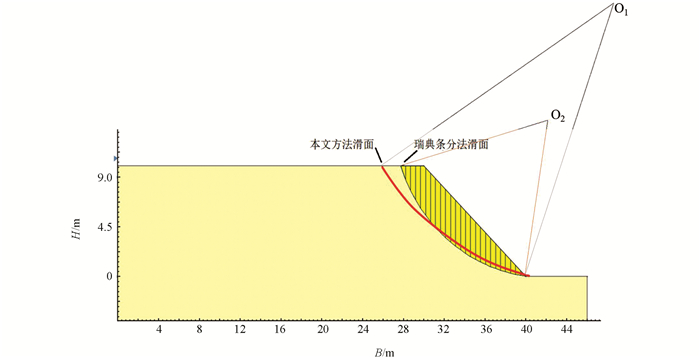
目前极限平衡法是边坡稳定性分析中最成熟、最方便、应用最广的方法,常用的极限平衡法有瑞典条分法、毕肖普条分法等,由于几种方法所算得的最危险滑面位置与安全系数较为接近,本文用瑞典条分法求解滑面,并与SPH方法进行比较分析.
图 12中,黑色实线圆弧表示用瑞典条分法获得的最小安全系数的圆弧,红色实线代表本文SPH最大剪切应变率粒子滑面,可见本文方法与瑞典条分发得到的滑面位置均通过土坡坡角,由于滑面形状预先的假设,瑞典条分法滑面是完美的圆弧形状,而本文方法求解的滑面为近似平滑圆弧曲线,其圆心O1距边坡外侧更远,半径更大. 本文方法得到的滑面位置更接近于使用作图法得到的滑面位置,即破坏面与大主应力作用方向(坡面)夹角θ=45°-φ/2.
-
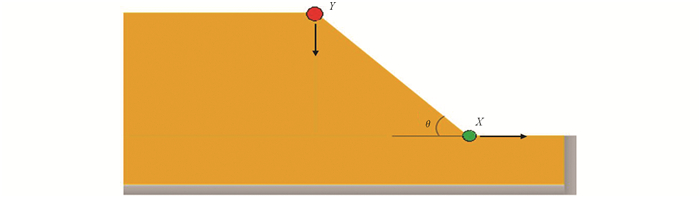
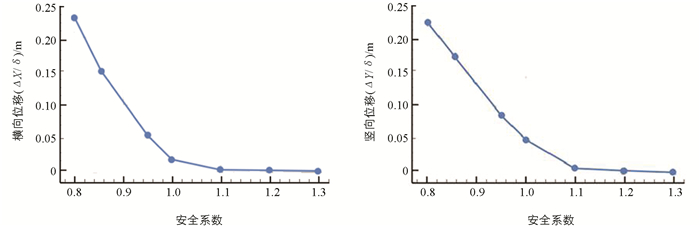
不同于判定滑面位置问题计算收敛的确定性,在SPH框架下土坡的稳定性分析需要首先确定整个变形过程中的极限平衡临界状态. 然而,SPH框架下土坡的稳定性分析的极限平衡临界状态,不是上述最大剪切应变率粒子贯通形成滑面时,而是在土坡塑性剪切区域形成过程中,故难以明确极限平衡临界状态. 本文从土坡安全系数与坡体位移量的关系出发,对土坡形变与稳定性关系作一定的探讨. 选取坡面上具有代表性两个位置的位移量:坡角水平位移(X)和坡顶竖向位移(Y)如图 13. 通过前述基于SPH的强度折减法,不断折减算例中岩土体材料的强度参数黏聚力c与内摩擦角φ,同时记录位移量X与Y,如表 2. 不同强度参数对应安全系数下横向位移与竖向位移水平如图 14所示.
由图 14可知,当安全系数接近1.1时,ΔX/δ与ΔY/δ都小于0.01,没有观察到较明显变形. 在安全系数逐渐减小的过程中,坡顶的竖向位移和坡角的水平位移呈现逐渐增大的趋势,与工程边坡中滑体后缘形成裂缝和前缘向前滑动的特征相对应起来. 反之,当安全系数小于1.0时,剪切带发育明显,边坡变形明显. 当安全系数接近1.0时,水平位移ΔX与坡面高度δ之比接近0.02,而竖向位移ΔY与坡面长度δ之比接近0.05,较前者大,造成二者差异的原因可能是在边坡初始状态,在粒子自重的影响下,SPH粒子间相互作用力与相互距离在计算初始阶段出现一定的调整引起的. 若认为极限平衡法的安全系数是可信的,则当安全系数为1.0时,土坡出现明显变形,ΔX/δ为0.018 8(<0.02),表明土坡在极限平衡状态下时,出现不明显变形;当安全系数小于1.0时,土坡开始出现明显变形(安全系数0.95,ΔX/δ为0.055 20).
综上所述,本文依据SPH对土坡变形过程连续求解的方式,可以确定土坡滑面的位置与形态,并且评估土坡稳定性与形变的关系. 传统的极限平衡法预先设定的滑面形状,考虑了满足力和力矩的平衡条件,忽略了岩土体应力—应变的关系,特别是变形的发展. 同时,由于忽略了失稳过程中岩土体应力—应变的关系,因而极限平衡法缺失了边坡的变形信息,但从实际工程的边坡监测中来看,边坡发生较大变形、出现较大位移时,边坡的平衡条件发生了变化,稳定性系数也随之改变;另一方面,极限平衡法的土坡滑动面是提前假设的,假设的滑动面是设定的而非精确计算的. 因此,与传统的滑面确定方法相比,基于SPH的滑面确定方法更能准确地预测在安全与危险边界处岩土材料的变形.
2.1. 土坡滑面的确定
2.2. 与极限平衡法滑面位置的对比
2.3. 土坡形变与稳定性分析
-
土坡滑面的确定对其稳定性分析起着决定性和控制性的作用. SPH方法作为一种能够连续求解岩土体整体变形过程的方法,在处理土体大变形方面具有较大的优势. 本文基于SPH算法框架下土体的理想弹塑性本构提出了土坡滑面判定方法,得出如下结论:
1) 从连续求解整个变形过程的视角出发,在全局搜索区域中划分单次搜索区间,依据强度折减法与最大剪切应变率原则,提出了滑面判定方法,得到了理想弹塑性本构土体下土坡的滑面,并与极限平衡条件下条分法所确定滑面进行了对比分析,本文方法求解的滑面为近似平滑圆弧曲线,其圆心距边坡外侧更远,半径更大;
2) 依据强度折减法,可通过SPH土坡全过程模拟方法初步分析土坡稳定性与土坡形变间的关系,与传统的滑面确定方法相比,基于SPH的滑面确定方法更能准确地预测在安全与危险边界处岩土材料的变形. 本文为土坡滑面确定与稳定性分析提供了一种新的、有效的方式,较极限平衡法与有限元法,本文方法能够从土坡滑面确定与稳定性分析中提取出土坡全过程变形信息,是此类问题分析较好的补充.



 下载:
下载: