高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

锂电池的电化学建模研究

,  , 

上一篇

下一篇

梁新成, 张志冬, 黄国钧. 锂电池的电化学建模研究[J]. 西南大学学报（自然科学版）, 2023, 45(3): 214-221. doi: 10.13718/j.cnki.xdzk.2023.03.018
引用本文: 梁新成, 张志冬, 黄国钧. 锂电池的电化学建模研究[J]. 西南大学学报（自然科学版）, 2023, 45(3): 214-221. doi: 10.13718/j.cnki.xdzk.2023.03.018
shu
LIANG Xincheng, ZHANG Zhidong, HUANG Guojun. Research on the Electrochemical Modeling of Lithium-ion Batteries[J]. Journal of Southwest University Natural Science Edition, 2023, 45(3): 214-221. doi: 10.13718/j.cnki.xdzk.2023.03.018
Citation: LIANG Xincheng, ZHANG Zhidong, HUANG Guojun. Research on the Electrochemical Modeling of Lithium-ion Batteries[J]. Journal of Southwest University Natural Science Edition, 2023, 45(3): 214-221. doi: 10.13718/j.cnki.xdzk.2023.03.018
shu

锂电池的电化学建模研究

  • 1.

    西南大学 工程技术学院，重庆 400715

  • 2.

    西南大学 人工智能学院，重庆 400715

  • 基金项目: 重庆市自然科学基金项目(cstc2021jcyj-msxmX1062)
详细信息
    作者简介:

    梁新成，博士，讲师，主要从事新能源汽车、机械振动和汽车动力学研究 .

  • 中图分类号: TM912

Research on the Electrochemical Modeling of Lithium-ion Batteries

  • 1.

    College of Engineering and Technology, Southwest University, Chongqing 400715, China

  • 2.

    College of Artificial Intelligence, Southwest University, Chongqing 400715, China

  • 摘要: 锂离子电池作为电动汽车重要的储能单元，在反复的充放电过程中出现性能衰退等老化现象不可避免. 本质上锂电池完成的充放电过程是持续的电化学反应，因此基于电化学建模方法比等效电路方法更为精准和可靠. 本文首先从理论上阐述了电化学建模的过程，然后应用COMSOL软件对模型进行了仿真，为验证仿真分析的可靠性，对18650锂离子电池进行了多个温度、倍率的充放电，将仿真数据与实验结果进行对比发现吻合较好，表明了电化学建模方法的可靠性较高. 随着放电倍率的增大，仿真结果和实验数据吻合变差，如何在建模时考虑电池的老化、热耦合等因素以确保始终吻合良好是未来研究的内容.
    Abstract: As an important energy storage unit of electric vehicles, performance degradation and other aging phenomena of lithium-ion battery are inevitable during the process of repeated charging and discharging. In essence, the charging and discharging process of lithium-ion battery is a continuous electrochemical reaction, so the electrochemical modeling method is more accurate and reliable than the equivalent circuit method. In this study, firstly, the process of electrochemical modeling was theoretically described, and then the model was simulated by COMSOL software. To verify the reliability of the simulation analysis, the 18650 lithium-ion battery was charged and discharged at multiple temperatures and rates, and the simulation results was compared with the experimental data. Since the simulation curve is in good agreement with the experimental data, it shows the reliability of the electrochemical modeling method. With the increase of discharging rate of current, the coincidence rate becomes worse. Consequently, aging and thermal coupling factors will be considered in the model to ensure a good coincidence rate as the content of future research.
  • 加载中

  • 图 1  锂电池的结构

    下载: 全尺寸图片 幻灯片

    图 2  电池电化学一维模型

    下载: 全尺寸图片 幻灯片

    图 3  基于变化电流的仿真结果

    下载: 全尺寸图片 幻灯片

    图 4  基于恒定电流的仿真结果

    下载: 全尺寸图片 幻灯片

    图 5  实验设备原理图

    下载: 全尺寸图片 幻灯片

    图 6  锂电池HPPC实验流程

    下载: 全尺寸图片 幻灯片

    图 7  新旧电池HPPC实验结果

    下载: 全尺寸图片 幻灯片

    图 8  仿真数据和实验结果对比

    下载: 全尺寸图片 幻灯片
  • [1] 江浩斌, 张旺, 陈龙, 等. 基于双电层结构的锂离子电池电化学建模[J]. 电池, 2018, 48(4): 244-248. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-DACI201804008.htm
    [2] 梁新成, 张勉, 黄国钧. 基于BMS的锂离子电池建模方法综述[J]. 储能科学与技术, 2020, 9(6): 1933-1939. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-CNKX202006039.htm
    [3] 李光远, 马彦. 锂离子电池电化学建模及其简化方法[J]. 吉林大学学报(信息科学版), 2018, 36(3): 260-268. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-CCYD201803006.htm
    [4] DOYLE M, FULLER T F, NEWMAN J. Modeling of Galvanostatic Charge and Discharge of the Lithium Polymer Insertion Cell[J]. Journal of the Electrochemical Society, 1993, 140(6): 1526-1533. doi: 10.1149/1.2221597
    [5] 冯毅. 锂离子电池数值模型研究[D]. 上海: 中国科学院, 2008.
    [6] DARLING R, NEWMAN J. Modeling Side Reactions in Composite LiMnO Electrodes[J]. Journal of the Electrochemical Society, 1998, 145(3): 990-998. doi: 10.1149/1.1838376
    [7] 张立军, 程洪正. 基于相似理论的锂电池三维电化学跨尺度建模[J]. 同济大学学报(自然科学版), 2016, 44(4): 605-613. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ201604016.htm
    [8] HAN X B, OUYANG M G, LU L G, et al. Simplification of Physics-Based Electrochemical Model for Lithium Ion Battery on Electrical Vehicle. PartⅠ: Diffusion Simplification and Single Particle Model[J]. Journal of Power Sources, 2015, 278: 802-813. doi: 10.1016/j.jpowsour.2014.12.101
    [9] HAN X B, OUYANG M G, LU L G, et al. Simplification of Physics-Based Electrochemical Model for Lithium Ion Battery on Electric Vehicle. PartⅡ: Pseudo-Tow-Dimensional Model Simplification and State of Charge Estimation[J]. Journal of Power Sources, 2015, 278: 814-825. doi: 10.1016/j.jpowsour.2014.08.089
    [10] YUAN S F, JIANG L, YIN C L, et al. A Transfer Function Type of Simplified Electrochemical Model with Modified Boundary Conditions and Padé Approximation for Li-ion Battery: Part 2. Modeling and Parameter Estimation[J]. Journal of Power Sources, 2017, 352: 258-271. doi: 10.1016/j.jpowsour.2017.03.061
    [11] 李涛, 程夕明, 胡晨华. 锂离子电池电化学降阶模型性能对比研究[J]. 物理学报, 2021, 70(13): 429-440. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB202113037.htm
    [12] 程麒豫, 张希, 高一钊, 等. 基于降阶电化学模型估算锂离子电池状态[J]. 电池, 2021, 51(2): 110-113. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-DACI202102002.htm
    [13] 徐文军, 胡芃. 基于电化学-热耦合模型的21700型锂离子电池充放电过程热行为分析[J]. 中国科学技术大学学报, 2020, 50(5): 645-653. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-ZKJD202005012.htm
    [14] 李夔宁, 谢运成, 谢翌, 等. 基于电化学热耦合模型的富镍锂离子电池产热分析[J]. 储能科学与技术, 2021, 10(3): 1153-1162. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-CNKX202103039.htm
    [15] SMITH K, WANG C Y. Power and Thermal Characterization of a Lithium-Ion Battery Pack for Hybrid-Electric Vehicles[J]. Journal of Power Sources, 2006, 160(1): 662-673.
    [16] CHATURVEDI N A, KLEIN R, CHRISTENSEN J, et al. Modeling, Estimation and Control Challenges for Lithium-ion Batteries[C] //Proceedings of the 2010 American Control Conference. June 30-July 2, 2010, Baltimore, MD, USA. IEEE, 2010: 1997-2002.
  • 加载中
图( 8)
计量
  • 文章访问数:  1857
  • HTML全文浏览数:  1857
  • PDF下载数:  896
  • 施引文献:  0
出版历程
  • 收稿日期:  2021-08-30
  • 刊出日期:  2023-03-20

锂电池的电化学建模研究

    作者简介: 梁新成，博士，讲师，主要从事新能源汽车、机械振动和汽车动力学研究
  • 1. 西南大学 工程技术学院，重庆 400715
  • 2. 西南大学 人工智能学院，重庆 400715
  • 收稿日期:  2021-08-30
基金项目:  重庆市自然科学基金项目(cstc2021jcyj-msxmX1062)

摘要: 锂离子电池作为电动汽车重要的储能单元，在反复的充放电过程中出现性能衰退等老化现象不可避免. 本质上锂电池完成的充放电过程是持续的电化学反应，因此基于电化学建模方法比等效电路方法更为精准和可靠. 本文首先从理论上阐述了电化学建模的过程，然后应用COMSOL软件对模型进行了仿真，为验证仿真分析的可靠性，对18650锂离子电池进行了多个温度、倍率的充放电，将仿真数据与实验结果进行对比发现吻合较好，表明了电化学建模方法的可靠性较高. 随着放电倍率的增大，仿真结果和实验数据吻合变差，如何在建模时考虑电池的老化、热耦合等因素以确保始终吻合良好是未来研究的内容.

English Abstract

    全文HTML

  • 开放科学(资源服务)标志码(OSID)：

  • 锂电池是电动汽车主要的储能单元，其质量优劣对电动汽车动力学等性能具有极大的影响. 汽车的行驶工况极为复杂，而锂电池的比功率、温度等指标还有待改进，否则会导致实际应用中出现过流、过压等问题，甚至酿成冒烟、燃烧、爆炸等恶性事故. 锂电池建模研究有助于提高其参数如荷电状态(state of charge，SOC)、健康状态(state of health，SOH)的估计精度，实现对电池的精准化管理并延长使用年限[1-2]，也一直是行业研究的焦点.

    针对锂电池的建模及理论分析，国内外已经取得了一些进展. 电化学模型主要分为准二维模型、单粒子模型、平均值模型等，其中最基础的是准二维模型[3]. Doyle等[4]在20世纪90年代就建立了最早的电化学模型——准二维电化学模型；冯毅[5]在准二维模型的基础上模拟了LiCoO2/MCMB电池体系的电流密度分布；Darling等[6]在准二维模型的基础上提出了电池容量老化模型；张立军等[7]基于电化学过程的相似准则，建立了三维跨尺度的模型；Han等[8-9]研究了固相和液相锂离子浓度的分布和电势分布，建立模型并分析了电池的老化状态；Yuan等[10]通过帕德近似方法进行扩散方程的降阶和边界条件的修正，得到了简化的电化学模型；李涛等[11]研究了锂离子电池电化学降阶模型的对比性能，以更少的参数实现较高的计算精度；程麒豫等[12]通过降阶的电化学模型，提高了估计的精度和收敛速度；徐文军和李夔宁等[13-14]对电化学-热耦合模型进行了综合分析并通过实验验证了结果. 与锂电池的等效电路模型相比，电化学模型的参数量大且包含多个偏微分方程，对其理论模型进行降阶并改进算法的收敛速度具有重要的工程应用价值.

1.   电化学模型的建立

    1.1.   锂离子电池的平均值模型

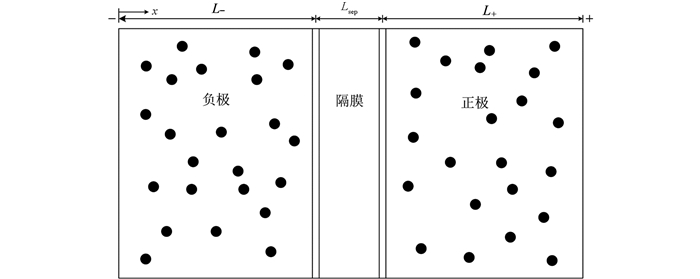
  • 准二维模型的通用性较好，更复杂的电化学模型都是在其基础上延伸和发展的，针对该模型做了如下的假设：①电池内部只有锂离子参与了化学反应，暂不考虑副反应的发生；②锂离子在固、液相中仅发生扩散和迁移，其液相的体积分数保持不变；③电极的活性物质视为半径相等的固体球形颗粒；④固、液相交界面处的电化学反应规律符合Bulter-Volmer方程. 为了对电池的SOC进行估计，论文将从准二维模型推导出平均值模型. 此外，电池以三维的形态存在，假定固相和液相的电势与浓度是均匀分布的，仅需要考虑其在x方向的变化. 电池的结构如图 1.

    在准二维模型中锂离子电池的端电压表达式为

    在式(1)中，φs为固相电势，Rf为电极表面膜电阻，I为输入的电流密度，L为电极宽度.

    根据参考文献[15]，固相和液相交界面处电化学反应产生的过电势与固相电势、液相电势及开路电压之间的关系为

    其中，η为球形颗粒表面过电势，φe为液相电势，U(cse(x))为与固相颗粒表面锂离子浓度有关的电极稳态开路电压，cse为固相和液相交界面处锂离子浓度.

    总电压等于锂离子电池的端电压与电池内部电化学反应之后的各相电势的代数和

    根据前述假设，球形颗粒表面的锂离子浓度可表示电池的荷电状态Soc，引入电极利用率

    其中Cse(t)为固相和液相交界面处的锂离子浓度，Cs，max为固相锂离子浓度的最大值. 则Soc可表示为

    其中θ0%和θ100%分别为电池完全放电及满电时球形颗粒表面电极利用率.

    • 1.2.   锂离子流量密度平均值求解

  • 考虑到固体球形颗粒是完全无差异的，故可任意取一个球形颗粒并认为锂离子固相扩散发生在其中，负极和隔膜界面xn处的液相电流密度为

    再根据液相电流密度ie|(xn)的边界条件ie|x=0=0和ie|x=xn=i可以得到

    由负极电荷守恒方程可得在0≤x≤xn时锂离子流量密度的平均值[16]

    类似可以推得在正极最右端L处的液相电流密度及在xp≤x≤L的锂离子流量密度平均值

    • 1.3.   电化学一维模型的建立与仿真分析

  • 应用COMSOL软件多物理场仿真以获得精确的分析结果，并能在一个环境中应用多种物理场对目标结构进行分析. 该软件建模的基本步骤如下：①全局参数定义. 全局定义主要是提供电池完整的物理参数如标称电压、最小放电终止电压、最大充电终止电压、电池容量等，通过时间管理可设定仿真时间. ②组件1的设置. 组件1的设置包括定义、几何、材料和电池接口，可按照提示逐一填写. ③变化电流和恒定电流的设置. 主要包括电流分布初始化和电流瞬态建立，其中电流分布初始化的计算与求解基于一次电流分布类型，确保求解过程简单和仿真结果准确. 而瞬态的建立与全局定义中的默认模型输入类似，主要参数为电解质、电流密度1、电流密度2、多孔电极1、多孔电极2等. ④求解器的配置. 主要分为编译方程、因变量1的设置. 恒定电流的求解相比变化电流不需要设置复杂的电解质浓度等，仅需设置锂离子电池物理场的控制参数，以及对变化电流中的电池放电倍率的参数化扫描.

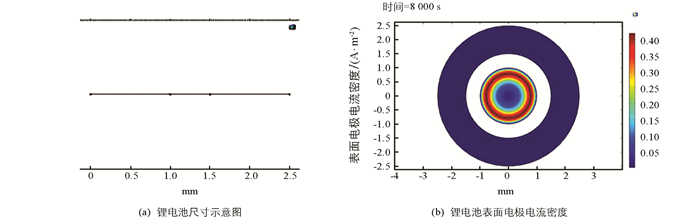
    结合前述的理论推导，应用COMSOL软件建模并通过对编译方程、恒定电流、变化电流及电流分布等参数的初始化及求解，得到图 2的一维模型. 其中图 2(a)为电池的尺寸示意图，可视为正极、负极和隔膜三部分；图 2(b)为电极电流密度分布规律，仿真的时间是8 000 s，右侧的云图表明红色之处的电极电流密度分布最大.

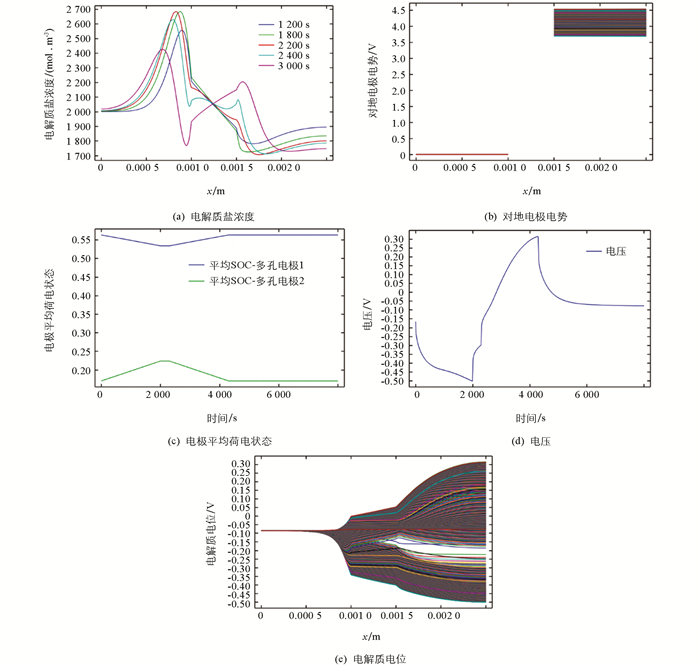
    运行模型可求得电解质盐浓度、对地电极电势、电极平均荷电状态、电压及电解质电位等结果，具体见图 3(a)-(e).

    锂电池工作时锂离子在电极之间传输，图 3(a)电解质盐浓度在负极升高而在正极降低，仿真时间越长则电解质盐浓度在负极越低，而在正极越高. 如3 000 s时的仿真曲线相比其他4条曲线的电解质盐浓度在负极最低，而在正极最高. 图 3(b)的负极电势为零，正极电势经过4 140 s放电后至3.6 V，其右侧密集的线段是以10 s为间隔的正极电势. 由于电池的电化学反应是由电解质材料与电极材料所决定的，当电池老化时其内部电化学反应减缓，锂离子电池容量逐渐衰减且内部电阻增大. 图 3(c)是多孔电极1和多孔电极2的平均荷电状态曲线，其中多孔电极1荷电曲线在前2 000 s呈缓慢下降趋势，在2 000~2 300 s荷电状态曲线保持不变，在2 300~4 300 s之间呈缓慢上升，而在4 300~8 000 s基本保持恒定. 多孔电极2荷电曲线除在前2 000 s缓慢上升和2 300~4 300 s缓慢下降外，其余与多孔电极1荷电状态曲线一致. 图 3(d)的电压曲线在前2 000 s呈下降之势，在2 000~4 300 s呈上升趋势，然后又下降到零，基本反映了锂电池的工作过程. 图 3(e)电解质电位曲线在负极分布于-0.08 V，在隔膜处分布于-0.4~0.05 V，而在正极分布于-0.5~0.3 V，曲线总体呈喇叭状.

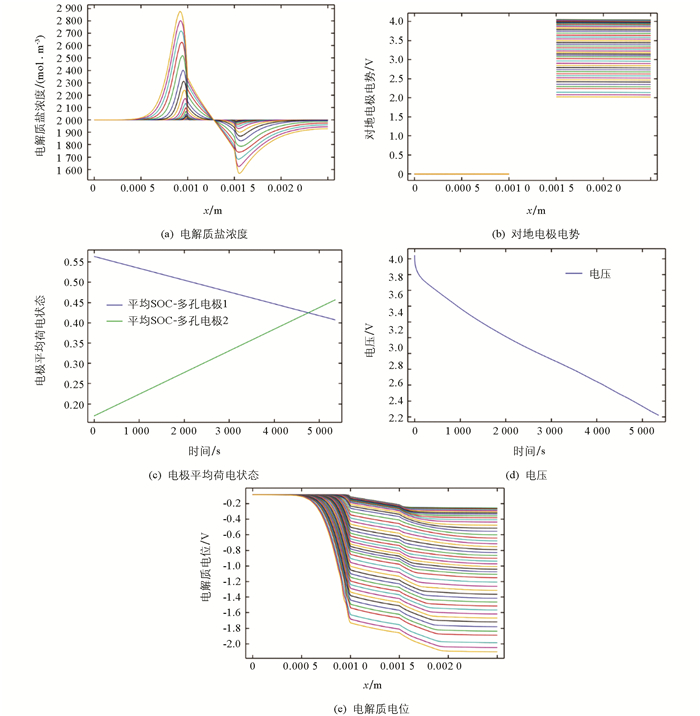
    当电动汽车匀速行驶时，则电池为恒定电流放电，类似于变电流的求解过程，图 4为一些参数的仿真结果.

    其中，图 4(a)的电解质盐浓度在负极达到最大，在正极最小，且波峰和波谷靠近隔膜两侧. 图 4(b)和图 3(b)相似，负极对地电极电势基本为零，正极对地电极电势随仿真时间的延长而电势降低. 图 4(c)中的多孔电极1和多孔电极2的平均荷电状态在0~5 500 s内皆为一条斜线，多孔电极1荷电状态曲线倾斜向下，而多孔电极2的荷电状态曲线倾斜上升. 图 4(d)的电压在0~5 500 s内呈现下降趋势，也近似为一条斜线. 图 4(e)的电解质电位曲线类似于图 3(e)，显著的区别是单侧下降，且电解质电位皆为负值.

    总之，对变化电流和恒定电流的仿真结果而言，各参数随时间的变化规律符合电池的工作过程，这也从侧面证明了模型的可靠性. 不足之处是建模时为了降低难度，前述模型并未涉及电池的老化、热耦合等因素，后续的研究应该一并考虑，使模型的仿真结果与实验数据始终吻合较好.

2.   电池充放电实验分析

    2.1.   实验的设备和原理

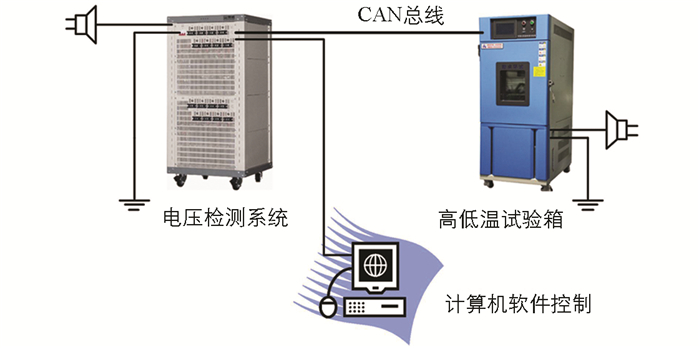
  • 由于锂电池电化学模型的参数较多，为简化计算过程做了较多的假设. 尽管前述的仿真结果在趋势上符合电池的工作过程，为了更精准地研究电池的充放电过程特点及规律，仍有必要进行实验测试以便对仿真结果进行验证，基于此搭建了图 5所示的实验平台，其主要包括电池高低温实验箱、电池充放电与电压检测系统、NEWARE仿真测试软件三大部分. 高低温实验箱为东莞勤卓环测高低温试验箱，该设备在-40 ℃~150 ℃均可按照温度的变化速度无极精准调节；电池检测系统采用新威CT-8000工况模拟电池检测系统；实验对象为H18650CIL型镍钴锰酸锂单体电池，其额定容量为2 400 mAh，额定电压是3.6 V，放电终止电压为2.75±0.03 V，充电终止电压为4.20±0.03 V，充电截止电流为24 mA，25 ℃最大的充电电流为1C(2 400 mA)，最大放电电流为2C(4 800 mA).

    • 2.2.   电池的HPPC充放电实验

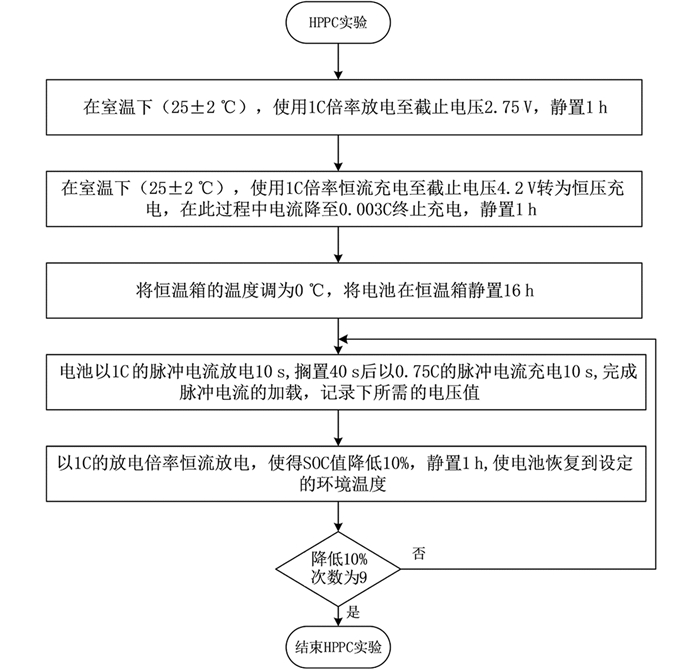
  • 混合功率脉冲特性(Hybrid Pulse Power Characteristic，HPPC) 实验通常用于对电池的放电循环特性及单体功率性能进行测试验证. HPPC实验的流程如图 6所示，为了对比电池的相关特性，选择了特斯拉早期使用的旧电池进行室温(25 ℃)下的HPPC实验.

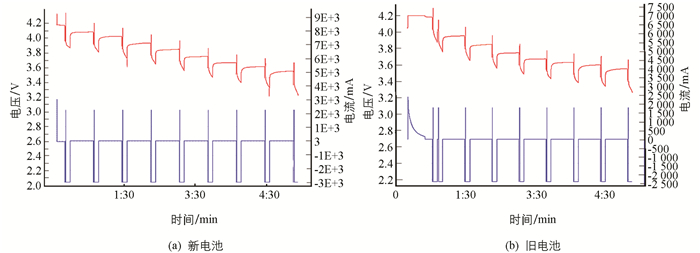
    HPPC实验的目的是得到实验所用电池在不同的SOC、不同脉冲时间下的放电和回馈脉冲功率的能力，此外，脉冲放电时间不同也会导致电池放电能力各异. 实验采用静置30 min后进行10 s脉冲放电，图 7为新旧电池的HPPC实验结果，其中红色曲线为电压，蓝色曲线为电流，新电池始放电阶段相比旧电池稳定平缓，这表明新电池单体功率性能比旧电池好.

    考虑到温度对电池内阻的影响，还在0 ℃和40 ℃下进行了新旧电池HPPC实验，限于篇幅不再单独列出. 通过对实验数据的分析可知：当环境温度过高或者过低时，电池充放电能力相比常温变差，而旧电池经过多次放电后其充放电能力明显下降，主要表现在电池内阻明显增加. 总之，电池在不同温度、电流和寿命状态下，其充放电能力是存在差异的.

    • 2.3.   电池恒流放电工况实验

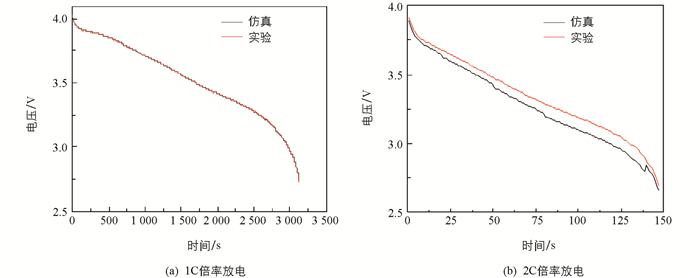
  • 当电池的放电倍率较大时难以精准描述电池内部化学反应的机理，为此，还进行了1C和2C的电流恒流充放电，以反映汽车在匀速行驶工况下的放电状况. 实验电池的额定电压是3.6 V，额定容量为2 400 mAh，将实验数据与仿真曲线进行比较，结果如图 8所示.

    图 8(a)仿真分析的电压与实验数据基本吻合，可以认为一维建模正确度较高. 图 8(b)相比1C放电倍率差异较大，原因是较大倍率放电时锂电池液相的锂离子扩散、液相离子传导和固相电子传导对电池的内部电化学反应影响较大所导致.

    和等效电路等理论模型相比，电化学模型能够更详细地描述锂电池工作过程中各参数的具体变化，但要在锂电池工作过程中准确地测试电流密度等参数目前存在较大困难，还需要在实验方案等方面进行完善. 因此，如何在不破坏锂电池物理结构的前提下测试更多的参数并与电化学仿真结果进行对比，是未来要进行研究的重要内容.

3.   结论

  • 1) 从准二维模型出发推导得到一维的均值模型，应用COMSOL软件可以进行建模.

    2) 仿真了电解质盐浓度、对地电极电势、电压等参数，能够准确反映电池的工作过程.

    3) 仿真模型与实验数据吻合较好，表明电化学模型较为可信，当放电倍率增大时吻合变差.

参考文献 (16)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回