-
开放科学(资源服务)标志码(OSID):

-
随着计算机科学技术的发展,汽车制造业逐渐从传统制造向智能制造转型. 汽车智能制造的关键环节包括汽车零件下料,也称为排样,是指将一系列不规则多边形零件不重叠地排放在给定的原板材上,目标是使板材利用率达到最高,当给定的原板材是定宽无限长板材时,该排样又称为二维不规则排样,此问题属于NP-HARD问题. 原始材料的利用率对企业的市场竞争和经济效益有很大影响,特别是在全球自然资源有限的情况下,最大程度地节约资源,确保企业可持续发展显得至关重要. 因此,该问题长期受到国内外研究人员的关注.
汽车零件排样属于二维不规则排样范畴,因此和传统二维不规则排样一样,明确待排零件的排样策略与排放次序是解决汽车零件排样问题的关键. 排样策略有“底左”策略[1]、“重心最低”策略[2]、“混合定位”策略[3]等. 确定定位策略后,问题就转化为所有待排零件排放顺序优化问题. 目前国内外大量文献都将排样算法与智能优化算法相结合解决排样次序优化问题. 汤德估等人[4]提出GEFHNA排样方法结合遗传算法和禁忌搜索算法优化排样顺序,选取ESICUP网站的通用数据集进行实验,仿真结果明显优于原始的GEFHNA排样方法;刘海明等人[5]提出小生境遗传算法来求解二维不规则排样问题,在遗传算法中引入排挤原理的小生境策略,改善了遗传算法的早熟现象;杨卫波等人[6]首次将实数编码的量子进化算法与不规则排样问题相结合,为不规则排样问题的求解提供了新思路;王静静等人[7]提出并行交叉遗传算法求解二维不规则排样,该算法构造两个种群进行杂交进化,同样改善了遗传算法的早熟现象;Burke等人[8]提出了一种改进型“底左”填充算法来解决传统“底左”算法的缺陷,并将其与爬山算法以及禁忌搜索算法相结合,对26个通用数据集进行了测试,表现出更好的排样性能;Rao等人[9]提出了混合分支限界禁忌搜索方法求解二维不规则排样问题,该算法将分支限界搜索的全局寻优能力和禁忌搜索算法的局部寻优能力结合,弥补两种算法的缺陷;Shalaby等人[10]使用基于实数编码的粒子群优化算法优化多边形的排放次序,改善了以往十进制离散编码容易早熟的现象. 然而,现有文献中用于求解二维不规则排样问题的优化算法大都有一定的缺陷,例如遗传算法容易早熟并且局部寻优能力差,模拟退火算法全局寻优能力较差等. 虽然后续论文在原有算法基础上进行了一定的改进,但是效果并不明显,并且大多数文献的实验都是选用ESICUP网站提供的通用数据集进行算法验证,并没有针对具体应用进行实际效果测试,利用改进智能优化算法对实际汽车零件排样进行研究,国内还未见相关文献报道.
二维不规则排样过程涉及大量多边形重叠计算以及靠接位置计算,现有多边形重叠检测算法的时间复杂度为O((M+N)log(M+N)),其中N和M为两多边形的边数. 为了提高算法的运行效率,有学者提出了临界多边形[11]的概念,排样过程采用临界多边形模型可以省略重叠计算,还可以提供待排零件所有可能的靠接位置. 基于上述分析,本文提出一种改进的免疫遗传算法,优化零件排放次序,使用临界多边形作为工具计算待排零件所有靠接位置进而基于“底左”策略选择排放点. 算法验证方面首先使用ESICUP网站提供的通用数据集测试,然后使用汽车生产厂商提供的实际汽车零件进行排样测试.
全文HTML
-
二维不规则排样要保证零件与零件不重叠、零件不超出原材料标示范围. 本文研究的是二维矩形带排样问题,即原材料定宽无限长. 假设待排零件集合为P={p1,p2,…,pn},n为零件数,pi表示第i个零件,O为允许的旋转角度集合,结合二维不规则带排样的目标及约束给出二维不规则条带排样的数学模型如式(1)所示:
式(1)中优化目标L为原材料长度,即寻找一种排样方案使得L最小;(x,y)表示零件二维坐标点;pi(oi)表示零件pi按角度oi进行顺时针旋转以后的坐标点集合;C(W,L)指原材料表示的坐标范围;W为原材料的宽度;约束条件中pi(oi) ∩ pj(oj)=Ø保证零件之间不重叠,pi(oi)⊆C(W,L)保证零件被排放在原材料内.
-
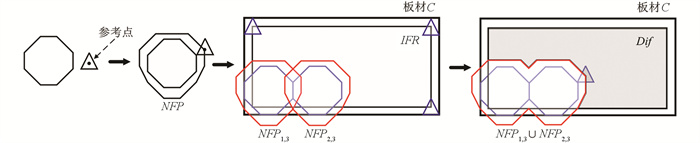
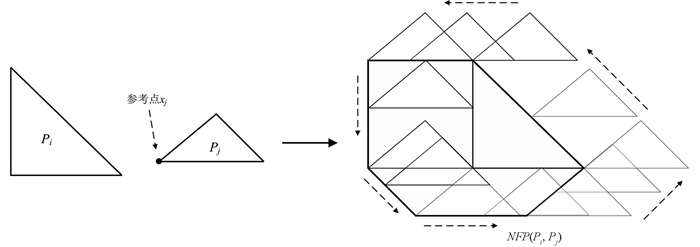
临界多边形(No Fit Polygon,NFP)[11]:给定多边形Pi,Pj,Pi静止,选Pj边上或内部点作参考点,将Pj不旋转地绕Pi滑动一周,滑动过程Pj始终与Pi相切,Pj上的参考点所形成的轨迹叫做Pj相对于Pi的临界多边形,记为NFP(Pi,Pj). 如图 1,xj为Pj的参考点:
NFP有如下重要特性:选取Pj的参考点在临界多边形内部时多边形Pi和Pj重叠;选取Pj的参考点在NFP边上时多变形Pi和Pj相切但不重叠;选取Pj的参考点在NFP外部时多边形Pi和Pj处于相离状态.
内靠接矩形(Inner Fit Rectangle,IFR)[12]:指多边形Pi在矩形C内部滑动过程参考点形成的轨迹,滑动过程中也要满足两多边形边不相交,如图 2所示:
依靠NFP与IFR可以计算待排零件在板材内部的所有靠接位置,假设P1,P2,…,Pi-1为已排零件,当前待排零件为Pi,原材料为矩形C,具体算法步骤如下:
步骤1 计算Pi与P1,P2,…,Pi-1的临界多边形,记为NFP1,i,NFP2,i,…,NFPi-1,i;
步骤2 计算Pi与C的内靠接矩形,记为IFRi;
步骤3 计算NFP1,i∪NFP2,i∪…∪NFPi-1,i,并集记为UnionNFP;
步骤4 计算IFRi-UnionNFP,差集多边形记为Dif,Dif边上点都是Pi的可排放位置.
计算示意图如图 3所示,假设待排零件为三角形,选取三角形的重心作为参考点,已排零件为两个正八边形,灰色区域即为差集多边形,边上所有点即为待排零件的可排放点.
上述算法省去了零件之间的重叠计算,只需将待排零件的参考点移动到差集多边形上某一点即可,排放就简化为基于差集多边形的定位选优过程. 基于该算法,如果较大零件之间产生孔洞,后续面积较小的零件还可以填充该孔洞.
-
重心临界多边形(Grivaty-NFP,GNFP)指选取滑动多边形的重心作为参考点构造的临界多边形. 同样,重心内靠接矩形(Grivaty-IFR,GIFR)的构造也选取滑动多边形重心作为参考点. 在多边形定位算法中,应用最多、最广泛的是“底左(Bottom-Left,BL)”[1]定位算法,其基本思想是将待排零件尽量往板材的最左最下角排放. 采用GNFP与GIFR模型计算排样点后,将待排零件放到最左最下位置,可以保证零件的重心位置最低. 零件的重心位置越低,越有利于降低整体排样方案的重心位置,从而有利于提高面积分布密度,提高原板材的利用率. 降低每个零件重心位置还可以使剩余板材的边界较为平缓,有利于后续零件的放置.
2.1. 临界多边形
2.2. 通过GNFP和GIFR选取BL排样点
-
遗传算法(Genetic Algorithm,GA)[13]是一种模拟自然界物种遗传进化机理的算法,具有很强的全局寻优能力,但是局部寻优能力较差. 免疫算法(Immune Algorithm,IA)[14]是受人体免疫学原理启发而提出的,该算法通过免疫选择、克隆及变异操作实现对解空间的局部搜索,因此具有很强的局部寻优能力. 若将两种算法结合,既可以继承遗传算法的全局寻优能力,又可以兼顾免疫算法的局部寻优能力.
-
遗传算法应用于二维不规则排样问题容易产生早熟现象,算法运行初期种群个体容易变得极为相似,这时交叉操作很难改变个体基因顺序,而变异概率往往取值很小,导致算法停滞. 文献[15]通过自适应调整遗传算法步骤,以及交叉、变异概率,有效避免了遗传算法产生早熟现象. 本文改进简化文献[15]的算法过程,在每次迭代进行交叉变异前根据平均适应度favg与最好适应度fbest的比值与δ的关系(δ一般取(0.9,1))修订相关操作及参数,如果比值小于δ,说明种群个体比较分散,则按传统遗传算法步骤先交叉再变异,如果比值大于等于δ,说明种群比较集中,交叉操作不易产生较大改变,这时增大变异概率,让变异概率等于交叉概率,先进行变异再进行交叉,可以帮助种群跳出局部解.
-
个体浓度表征种群多样性. 个体浓度偏高意味种群中相似个体较多,种群会集中在某一区间,不利于全局搜索,因此算法应对浓度过高的个体进行抑制,保证种群多样性. 个体浓度一般定义为:
D(pi)表示第i个个体的浓度;N为种群规模;s(pi,pj)表明个体pi与pj之间是否相似,相似取值为1,否则取值为0. 具体公式如下:
a(pi,pj)表示个体pi与个体pj的相似度;δs为相似度阈值;d为解的维度;pik为pi的第k维度. 个体之间相似度计算根据个体编码方式不同采用不同的计算方式. 本文个体采用十进制顺序编码,所以采用基于海明距离[16]的计算方法. 综合考虑适应度和浓度,计算种群所有个体激励度的方法如下:
S(pi)为个体pi的激励度;F(pi)为pi的适应度;α和β为权重系数,满足α + β=1,用于调节个体适应度和浓度对激励度的影响. 进行选择操作时,根据种群个体激励度进行选择可以有效保证种群的多样性.
-
人工免疫算法免疫选择操作需要选择种群中的个体进行克隆,假设每次迭代选择的个体数N固定,如果N取值较大会影响算法的运行效率,取值较小会影响算法的收敛精度. 所以N的取值很关键,本文通过自适应调整N的取值来确保算法的效率以及精度,具体公式如下:
Savg(G)为第G代种群平均激励度;SG(pi)为第G代个体pi激励度;n表示种群规模;M(G)表示克隆选择出的个体集合.
选择出的个体需要进行克隆操作,假设每个个体复制出Nc份,同样Nc取值太大影响算法运行效率,取值太小影响收敛精度. 通过自适应调整Nc的值能够提高算法的运行效率,具体公式如下:
C(pj)为个体pj克隆出的个体数;ω为克隆系数;CL免疫选择的个体数;int()表示向上取整操作.
-
基于以上分析,本文使用的改进免疫遗传算法(IGAA)具体步骤如下:
步骤1 设置参数,初始化种群,计算初始种群的适应度;
步骤2 判断是否满足终止条件,若满足输出最优解并停止迭代,否则执行步骤3;
步骤3 计算种群平均与最高适应度favg,fbest,如果favg/fbest≤δ,则执行步骤4,否则执行步骤5;
步骤4 种群进行交叉变异操作,计算子代适应度、浓度,根据式(4)选择产生新一代种群;
步骤5 临时调整变异概率等于交叉概率,种群进行变异交叉操作,计算子代适应度、浓度,根据式(4)选择产生新一代种群;
步骤6 根据式(5)(6)计算免疫选择操作需要选择出的个体数量,并进行免疫选择操作;
步骤7 根据式(7)计算经免疫选择的个体需要复制出的数量,并进行克隆操作;
步骤8 将步骤7中复制出的个体进行变异操作;
步骤9 克隆抑制操作,计算步骤8中变异后每个个体的适应度,保留适应度最高的克隆变异个体,如果其适应度比原克隆体适应度高就进行替换. 否则不替换,并转步骤2.
3.1. 自适应遗传算法设计
3.2. 改进选择操作
3.3. 自适应免疫选择与克隆
3.4. 改进免疫遗传算法步骤
-
优化算法首要解决的问题是个体的编码问题,本文采用十进制顺序编码,例如某个体编码:[(1,90),(2,90),(3,180),(4,0),(5,90)],每一个基因由两位组成,第一位表示零件编号,第二位表示对应零件的旋转角度.
-
本文采用顺序循环交叉:两个父辈个体P1,P2交叉产生子代个体Son1,Son2,先生成随机数pos1,pos2,P1,P2个体[pos1,pos2]之间的基因不变. 以Son1为例进行说明:遍历P2个体的基因,并赋给P1的[0,pos1)和(pos2,N),遍历过程中若P2的基因已经在P1的[pos1,pos2]之间出现则直接跳转到P2的下一位,Son2同理. 具体操作如下:假设pos1=2,pos2=5,并且有两个父代个体P1,P2:
P1,P2中加下划线的表示不变的基因位,交叉后产生子代个体:
-
本文基因的变异方法使用以下3种:
序号插入法:随机选取染色体中的某一位基因插入到随机位置,设染色体:[(1,90),(2,90),(3,0),(4,180),(5,270)],假设将下标为1的基因插入到下标为3的位置,插入后变成:[(1,90),(3,0),(4,180),(2,90),(5,270)].
两个零件交换位置:随机选取两位基因交换位置,设染色体:[(1,90),(2,90),(3,0),(4,180),(5,270)],交换下标为1和下标为3的基因,交换后变成[(1,90),(4,180),(3,0),(2,90),(5,270)].
两组零件交换顺序:随机选取两组基因交换位置,先对染色体基因进行分组,将染色体基因分成若干个一组,然后随机交换两组基因的位置.
前两种变异方式适用于小规模零件的排样,第三种方式适用于大规模零件的排样.
上述3种变异方法是对个体基因顺序变异,如果不对角度变异就无法产生新的旋转角度. 角度变异通过随机选择基因位,然后根据可旋转角度随机修改该基因位的角度值. 每次进行角度变异时,随机选择int(numPieces/10)位基因进行角度变异,其中numPieces为待排零件的数量.
-
本文研究的是二维矩形带排样问题,即原材料是定宽无限长,排样的目标就是使排样方案所切割的板材长度尽可能短,所以个体适应度表示如下:
上式pi表示第i个个体;Pj表示第j个零件;A(Pj)表示第j个零件的面积;L为切割的板材长度; W为板材宽度.
-
假设种群规模为M,交叉概率Pc,变异概率Pm,pbest用于记录每次迭代种群中适应度最高个体. 迭代过程中,若出现超过K代种群最优解未发生变化,说明算法陷入极值点,此时对种群中除最优个体外所有个体进行变异以便种群跳出局部极值.
步骤1 构造初始种群并计算种群适应度,记录适应度最高的个体到pbest中;
步骤2 判断是否满足终止条件,若满足则输出最优解并停止迭代,否则执行步骤3;
步骤3 计算当前种群平均适应度favg以及适应度最高个体fbest,如果favg/fbest≤δ,则执行步骤4,否则执行步骤5;
步骤4 将种群个体随机组合,遍历每一对个体,根据交叉变异概率进行交叉变异操作,转向步骤6;
步骤5 临时让Pm=Pc,将种群中的个体随机组合,遍历每对个体,根据变异交叉概率进行变异交叉操作,转向步骤6;
步骤6 计算交叉变异后子代个体的适应度,将子代与父代合并,计算所有个体浓度以及激励度,选择激励度最高的前M个个体形成新的种群;
步骤7 计算免疫选择出的个体数量,进行免疫选择以及克隆操作;
步骤8 对所有克隆出的个体进行变异操作并计算变异后所有克隆体的适应度;
步骤9 克隆抑制,将变异个体中适应度最高个体与原个体适应度比较,如果比原个体高就进行替换,否则不替换;
步骤10 若新种群中适应度最高的个体比pbest的适应度更高,更新pbest,否则判断是否超过K代pbest未更新,是则需要对种群中除适应度最高个体外的所有个体进行变异,否则转步骤2.
4.1. 编码方法
4.2. 交叉算子
4.3. 变异算子
4.4. 适应度计算
4.5. 算法步骤
-
为了验证算法的可行性及性能,本文下载ESICUP的14个基准问题来测试算法性能,然后使用汽车生产厂商提供的汽车零件图测试本文算法. 本文算法仿真使用的计算机为PC机,处理器为AMD R7 5800H,基准频率为3.2 GHz,内存为16 G,Win11操作系统,在VisualStudio2017平台进行,使用C++作为仿真语言. 本文将每个测试用例测试30次,记录最优结果以及平均结果. 相关参数以及操作说明:
1) 初始化参数说明:IGAA中的免疫克隆操作后会对所有克隆体进行适应度评估,为了保证算法收敛速度,种群规模不宜太大,设置种群规模为12. 交叉概率过小不利于种群特征遗传,变异概率过大会使算法近似于随机搜索,因此交叉概率设为0.9,变异概率设为0.1;阈值δ和δs一般取接近1的数,本文δ=δs=0.95;在能够找到最优解的情况下尽可能减少迭代次数以减少算法运行时间,因此最大迭代次数设为200次;克隆系数与种群规模有关,为了保证每代都能产生克隆体,本文ω=20,激励度计算的权重系数α=0.9,β=0.1;在迭代过程中,若出现超过K代种群最优解未发生变化,说明算法陷入极值点,此时对种群中除最优个体外所有个体进行变异操作以便种群跳出局部极值,K取值太大起不到作用,取值太小算法随机性太强,本文K=15.
2) 本文取零件数为30,60为分界值,当小于30时零件数较少,以相同概率采取4.3部分所述的前两种变异方式;大于30小于60时以0.4的概率采取第三种变异方式;大于60时,以0.9的概率采取第三种变异方式.
3) 种群初始化:种群初始化方法包括按零件面积递减、递增排序;按矩形度递减、递增排序;按零件长边递减、递增排序;其他个体随机产生.
-
目前,用于求解二维不规则排样的优化算法大多都是遗传算法(GA)、模拟退火(SA)等,因此本文首先选取3种传统优化算法GA、SA、IA以及近几年被提出的鲸鱼优化算法(WOA)[17-18]、乌鸦搜索算法(CSA)[19-20]等5种优化算法与IGAA进行比较,其中WOA与CSA解的编码方式使用文献[10]中的方法,对比结果见表 1. 其次,本文还将IGAA与文献[9]的混合分支限界禁忌搜索算法(BSTS)以及文献[21]的混合遗传模拟退火算法(GSAA)进行对比,结果见表 2. 表中Best表示运行的最优利用率;Avg表示运行的平均利用率;Dev表示算法最优结果与平均结果的差值;最后一行的Tot Avg表示14个数据库对应指标的平均值. 从表 1可以看出,混合IGAA算法无论在最优利用率还是平均利用率方面都要优于单一智能优化算法.
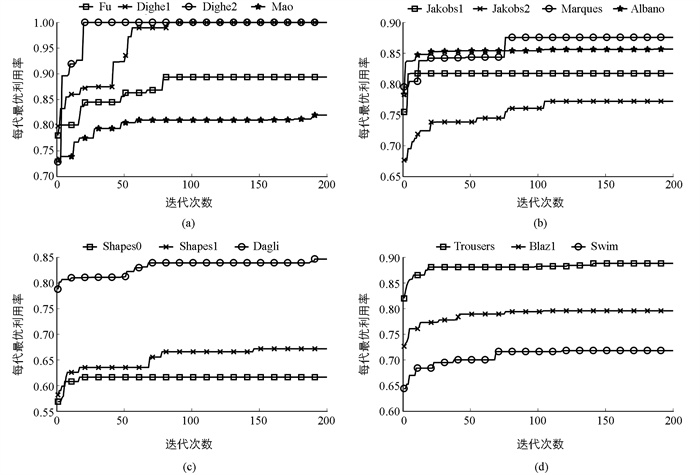
分析表 2中14个数据集的运行结果,IGAA在10个数据集的最优利用率结果高于BSTS的最优利用率;IGAA在9个数据集的平均利用率高于BSTS的平均利用率,其中Dighe1、Dighe2、Dagli数据集的平均利用率比BSTS的最优利用率都要好;与GSAA比较,IGAA的所有数据集,无论是最优优利用率还是平均利用率,都比GSAA的要高;分析总体平均Total Avg值,无论是最优利用率还是平均利用率,IGAA均为最高;算法稳定性方面分析每一行Dev的值,由于Dighe1、Dighe2属于“拼图”类型的排样,零件数较少,所以IGAA的平均利用率与最优利用率相差很大,但是随着数据集规模的增大,IGAA算法的稳定性要比BSTS、GSAA的稳定性要好. 图 4展示了算法运行所有数据集的收敛曲线:
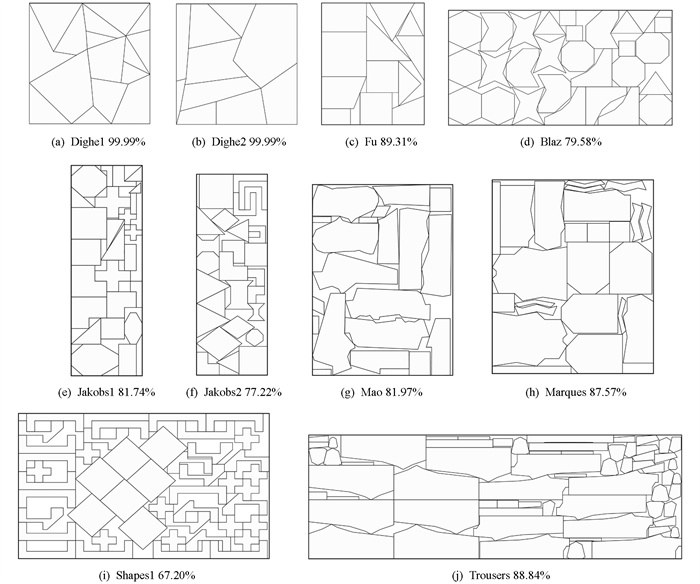
分析图 4,Fu、Dighe1、Dighe2、Jakobs1、Marques、Shapes0曲线可以在100代内收敛;Albano、Jakobs2、Shapes1、Blaz1、Trousers、Swim曲线可以在150代内收敛,Mao、Dagli曲线在150代以后出现轻微变化. 总的来说IGAA可以在150代以内收敛到一个不错的解. 图 5展示了几个基准数据集排样图.
-
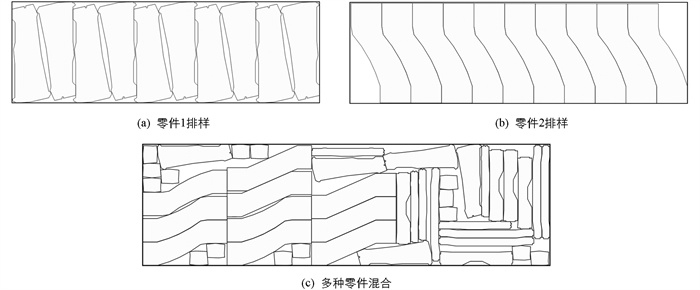
为了验证本文算法的实用性,本文选取重庆某汽车装配制造公司提供的汽车零件数据进行算法测试. 实际生产当中,往往需要对单一零件进行排样,因此本文测试单一零件的排样以及多种零件的混合排样,并将本文算法的运行结果同开源软件SvgNest以及5.1节的GA、IA、SA、WOA、CSA的运行结果进行对比,将每个汽车零件数据集运行20 min并记录最终结果,对比结果见表 3.
从表 3可以看出,无论是单一零件还是多种零件混合排样,IGAA算法仿真结果都要优于其他算法的仿真结果. 表明本文的IGAA算法具有一定的实用性. 图 6为IGAA算法的排样结果.
5.1. ESICUP的通用数据集测试
5.2. 实际汽车零件排样测试
-
本文针对二维不规则排样问题,使用基于重心临界多边形选取“BL”排放点,保证将待排多边形排放到重心最低的位置;在确定定位规则后,问题就转化为基于序列的优化问题,对于此,本文提出一种改进的免疫遗传算法,兼顾了两者的全局与局部寻优特性,并且自适应调整算法的运行步骤及相关参数,从而有效避免算法的早熟现象. 对相关基准问题测试,表明了该算法的有效性. 对于实际汽车零件的排样,本文算法表现出的排样效果也优于开源软件SvgNest和现有5种智能优化算法的排样结果. 总的来说,本文提出的IGAA算法在解决汽车零件排样问题方面具有一定的应用价值.



 下载:
下载: