-
开放科学(资源服务)标志码(OSID):

-
精准农业是许多发达国家和发展中国家十分关注的方向,精准农业的实现需要以尽可能完备、齐全、精确的农田信息为基础,其中包含了土壤、作物、微气象等信息,信息获取是精准农业能够大范围应用并获得高经济收益的基本保障[1]. 光谱[2]信息是农业信息的主要采集内容,其主要采集方式有无人机[3-5]空中采集和地面人工架设光谱设备采集. 前者存在大量的图像拼接工作,不仅增加了数据处理的工作量,还可能带有一定的累计误差,且价格较昂贵;后者需要人力架设设备进行数据采集,人力采集过程中需要随时移动设备并调整设备高度、角度等,费时费力,采集效率低下. 随着果园机械化、智能化水平的发展[6],具有调平功能的作业平台[7-8]对于农业生产的意义愈发重要.
国外对自动调平平台研究起步较早,技术相对成熟,已经研发了适用于各种情况的多自由度并联机构[9-10]. 以斯图尔特平台为代表的并联机构[11]平台,有刚度大、无累计误差、动态特性好等优点,被认为是理想的平台类型,但运动耦合程度高、控制难度大[12]的缺点也使得该平台的应用受到了限制. 其他具有调平功能的实际产品,比如澳大利亚Crendon Machiner公司生产的Squirrel系列工作平台[13]、英国NP Seymour公司生产的Windegger Picking Platforms[14]工作平台,行走部分都采用了轮式结构,动力源有液压和纯电驱动多种形式,但只能应用于平整度和通过性较好的果园中. 日韩等国因丘陵地区较多,更多使用履带式行走机构和液压执行元件. 在国内相关研究中,樊桂菊等[15]研究了拖拉机牵引的悬臂式调平平台,非行进状态调平后最大误差为1.74°,吕昊暾等[16]针对调平平台进行了自动调平前馈PID控制算法的研究,运动过程中仰角最大误差为3°. 目前采用的大多是液压驱动[17-18]的调节方式,且多数只有俯仰方向的运动,然后通过二次调平[19]的方式进行调平. 上述装置的液压执行机构能耗高、执行滞后、超调且自重大、调平精度差,仅有俯仰方向调平功能,需要手动对齐斜坡而不能完全自动调平,无法满足丘陵山地复杂工作环境下信息采集设备的需求.
因此,设计一种可以在丘陵山地复杂工作环境下搭载信息采集设备的全向自动调平平台,对于提高丘陵山地作物信息采集效率,降低设备移动架设的劳动强度有重要意义.
全文HTML
-
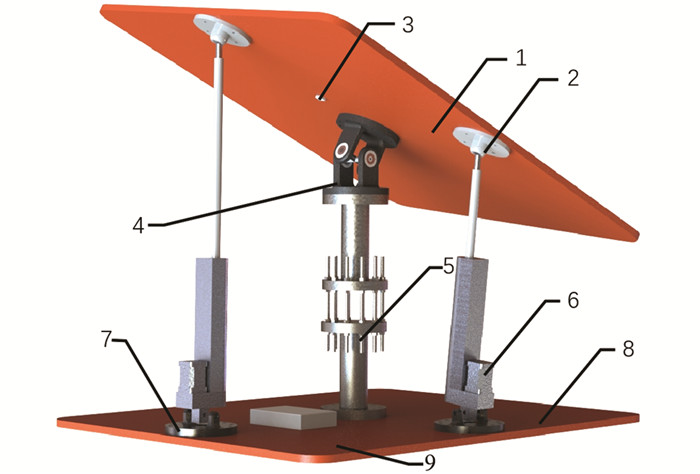
平台三维模型如图 1所示,机械结构主要包含上平台、下平台、立柱、两个直线推杆和其他连接件. 整体而言,该机构属于并联机构,能有效保证平台的强度与刚度. 推杆一端通过铰支座与下平台铰接,另一端通过球铰与上平台铰接,同一平面的3个连接中心点为直角三角形的3个顶点. 仰角方向推杆支座距中心位置380 mm,滚角方向为480 mm,立柱与万向节总高730 mm.
根据自平衡平台的结构可知其运动特性与并联机构一致,该平台是为搭载作物信息采集设备,实现在丘陵山地地区替代人工架设采集设备而设计的. 下平台固定在可行走的履带车底盘,并随之移动,根据丘陵山地的坡度变化进行自动调平,其设计要求如下:
(1) 平台额定负载为50 kg;
(2) 调平横滚、俯仰两个方向上的倾斜角度,正常工作范围为±15°,极限工作范围±18°;
(3) 静态调平精度小于等于0.3°,动态调平精度小于等于3°.
-
平台倾斜角度可分解为仰角与滚角,由两个直线推杆进行控制,当需要进行调平工作时,由传感器获取当前上平台姿态角度,单片机判断计算后发送信号给驱动器,驱动对应的推杆电机执行运动,在驱动过程中依据传感器反馈的姿态信息进行实时调整,两个方向相互叠加后可形成各个方向不同角度的倾斜,最终达到调平位置.
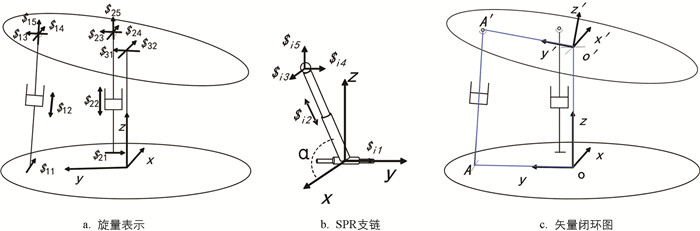
如图 2a所示,两条SPR支链(S为球副,P为移动副,R为转动副)与支撑轴分别与上下平台连接,SPR支链的旋转副轴线互相垂直,移动副驱动平台运动,建立如图 2a的并联机构运动螺旋系[20].
根据旋量理论,$ij表示第i个链上的第j个运动副对平台施加的约束螺旋,Li为第i个SPR支链的长度,α,β为支链与各自坐标系x轴的夹角. 在机构的不同位姿下,以其中一个SPR支链为例,如图 2b所示,可得出各运动螺旋系和反螺旋系,其中支链1的运动螺旋为:
对U1求互易积可得支链1的反螺系:
同理可得:
对于U链(U为万向副),其运动螺旋为:
对U3求互易积得反螺旋有4个:
式中,$1r表示约束力,该作用力平行于x轴且作用点过球副中心;$2r是平行于y轴的约束力;$31r,$32r,$33r分别为平行于x,y,z轴的约束力,且作用点过U副中心;$34r为力偶,其方向沿U副法线方向. 对于上平台而言,它受到了5个约束力和1个约束力偶的共同作用,其中$1r,$2r分别与$31r,$32r平行,即线性相关,则上平台有2个过约束. 因此机构自由度为上平台绕着万向节的x轴旋转和y轴旋转. 机构自由度可根据修正的G-K公式[21]计算:
式中,M为机构自由度,n为构件数,g为运动副数,fi为第i个运动副的自由度,μ为过约束数目. 在本文中n=6,g=7,μ=2. 计算可得即M=2,与螺旋理论分析结果一致. 综上所述,上述机构有着2转动(2R)的工作能力,其自由度为2.
-
运动学上主要通过寻求逆解的方法对并联机构进行分析,即已知动平台位姿,求解各执行关节变量. 设下平台中心为坐标系o-xyz的坐标原点,y轴指向支链1,x轴指向支链2,坐标系o′-x′y′z′则为上平台的平台中心,x′,y′与下平台指向一致,支链1与上下平台连接点为A,A′,支链2与上下平台连接点为B,B′,如图 2c所示,则o′-x′y′z′相对于o-xyz的旋转变换矩阵为:
其中α,β分别为绕x和y轴转角,在本文中分别为滚角和仰角.
从图 2c可看出,SPR支链的腿长L1,即移动副P的长度.
其中
$\overrightarrow{o^{\prime} A^{\prime}}$ 在坐标系o-xyz中表示为$R_{x y} \overrightarrow{O^{\prime} A^{\prime}}$ ,带入上述公式,故:通过上式可知,旋转矩阵Rxy与位姿相关,其余为构件尺寸长度. 需要指出的是,一般情况下默认的静平台是保持不变的,即下平台,而本文所研究的下平台是随地面起伏而变化的. 设计要求为±15°可达位姿,将极限角度代入,机械结构上
$\overrightarrow{o o^{\prime}}$ 长度为730 mm,$\overrightarrow{o^{\prime} A^{\prime}}, \overrightarrow{o A}$ 长度为480 mm,$\overrightarrow{o^{\prime} B^{\prime}}, \overrightarrow{o B}$ 长度为380 mm,则:即推杆行程至少为248.4 mm,考虑到行程和负载需求一定的余量,行程选用300 mm,计算可得整体极限位姿约为±18°.
1.1. 总体结构和要求
1.2. 调平工作原理
1.3. 推杆行程及控制调整极限角度
-
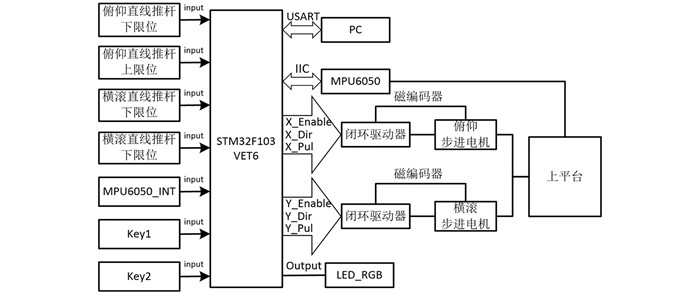
调平平台的控制系统部分采用单片机控制,主控芯片为STM32F103VET6,推杆、姿态传感器、步进电机驱动参数如表 1.
驱动器与推杆电机同轴安装,接收单片机脉冲信号后对步进电机进行驱动,在步进电机轴尾部加装径向磁铁用于驱动器的板载磁编码器读取反馈. 姿态传感器自身坐标系x轴、y轴分别与上平面仰角、滚角平行安装. 自动调平控制原理图如图 3.
目标控制角度默认为滚角、仰角都为0°,当姿态传感器检测到上平台角度与设定角度不一致时,控制器通过脉冲、使能和方向3个输出信号控制相应驱动器工作,驱动器则驱动直线推杆电机并保证其不丢步与正常情况下不堵转,其中脉冲频率决定电机转速,使能决定是否运动,方向决定电机旋转方向. 主控芯片开发环境为Keil5,C语言,在程序编写时,启用MPU6050的DMP特性,降低主控MCU的计算压力并在有新数据的时候在INT引脚上产生中断信号,其中包含了卡尔曼滤波算法. 控制系统结构如图 4.
-
板上外设选用了GPIO、串口通讯、IIC通讯和定时器,其中GPIO用于限位、启停按钮、驱动器使能、方向、LED,串口通讯用于连接电脑便于监控系统状态,IIC通讯用于MPU6050与主控芯片的通讯. 定时器为高级定时器TIM8,使用两个通道用于脉冲输出,其挂载于APB2总线,时钟频率fTIM8_CLK为72 MHz. 预分频因子TIM_PRESCALER设定为3,初始计数溢出值为0XFFFF,向上计数,不分频,重复计数器设置为0,使用比较输出模式,极性为高电平,互补通道也为高电平,空闲电平为低电平. 设置快速下计数翻转值为90,慢速为360. 翻转频率以下式进行参数计算:
在偏离设定位置角度大于0.2°的情况下,推杆电机将使用快速模式,此时步进驱动器接受到的脉冲频率为100 KHz,而慢速情况下为25 KHz. 42步进电机闭环典型矩频特性曲线[22],以雷赛公司的同类产品为例,在转速500 rpm时对应的脉冲频率在32细分下约为53 KHz,本文采用的低速运行频率25 KHz,约为235 rpm,经过减速后推杆末端执行速度约为3.5 mm/s,高速100 KHz,约为938 rpm,经过减速后推杆末端执行速度约为14 mm/s,均处于典型矩频特性曲线中扭矩较高位置.
-
程序设计是控制系统的核心部分,对系统有重大影响,程序主要循环由传感器与主控的通讯、两轴的插补和外部可视化3部分组成. 姿态传感器将姿态信息传递到主控芯片后,插补程序进行响应,同时外部LED灯进行周期闪烁表示调平过程的进行. 在系统开始运行时,程序将会对系统进行初始化,包括板上外设和传感器的初始化,然后在启动调平功能后开始循环调平,该程序流程图如图 5所示.
为了保护平台上的设备,整体动作过程要求尽量平稳且快速. 本文采取直线插补[23]的方式进行调平,在调平过程使用逐点比较法,使整个过程按照一定的步骤向平衡方向靠拢. 直线插补示意图如图 6所示.
假设调平过程在第一象限中,目标点设为g,以固定的步长1进行移动. 初始偏差为y方向进给步数的负值,每次进给后若偏差为正,则减去y轴进给步数,若偏差为负,则加上x轴进给步数. 依照此算法,偏差为正时,点在直线上方,偏差为负时,点在直线下方. 第一步固定为x轴(x,y方向都有进给量时),即到达a点,在此时对比期望的运动路径,a点位于其下方,进而更换进给轴为y,到达b点,循环对每个点与期望路径的相对位置进行偏差计算,最终达到平衡位置g.
同理,当调平过程位于其他象限时,仅需调整进给方向即可映射到第一象限. 首先判断插补方向,方向确定后按照第一象限插补方式进行直线插补,每次进给后都对比偏差和余步数量,从而决定是否更换进给轴和是否完成插补.
2.1. 控制系统设计
2.2. 硬件资源分配、配置和电机矩频特性分析
2.3. 程序设计和调平策略
-
根据丘陵山地的坡度变化范围,平台滚角和仰角设计调平幅度为±15°. 为减轻整车质量和保证强度,上下平台选用800 mm*1 000 mm*15 mm的强化工程塑料制成. 使用两个维特智能SINDT-TTL倾角仪分别测量上平台和下平台的角度数据(全范围精度为0.1°,分辨率0.01°,可同时测量两轴数据),自带上位机软件采集数据并保存.
-
室内试验方法:将自平衡平台下支撑平板固定在实验平台上,首先调整上下平台平行,关闭控制调平功能后,手动将试验平台仰角与滚角分别调整为指定角度,以圆形哑铃片为重物放置于上平面,在不同载重质量下进行重复实验. 同时打开控制系统与测量装置,记录上平台从设置角度自动调整至平衡所需时间和实际调平角度. 数据记录如图 7所示.
由图 7可知,调整时间随着调整角度的增大而增长. 仰角最大调整自动调平时间为8.94 s,最大绝对误差0.2°;滚角最大调整自动调平时间为8.42 s,最大绝对误差0.27°. 当调整角度较小时,绝对误差与负载重量关系较弱;当调整角度较大时,绝对误差随着负载的增大而有增大的趋势. 已知调平角度与平均调平时间的比值即为调平速度,可以看出调平速度随载重的变大有一定程度的降低. 在大载重时,其调平数据曲线有不同程度的在平衡位置波动,其主要原因是传感器的数据波动和执行机构存在装配间隙.
-
室外动态实验选取西南大学校内的一段坡度在0°~18°变化的地形进行测试,如图 8所示,自平衡平台固定于桑普农机生产的3BD-350型行走平台(最高速度2.6 km/h,装载负荷350 kg,车体规格20 10*1 160*1 240 mm)的适合位置,采用两种测试方法对平台进行试验.
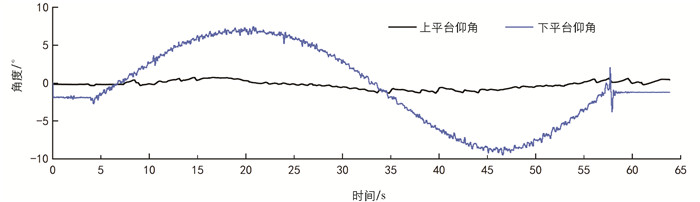
测试方法一为行进测试,首先对测试仪器进行水平校准,然后从起始位置打开数据记录(采样频率50 Hz),行驶方向为从坡底向坡顶驾驶(速度2 km/h),越过坡顶后再行驶一段时间后停止记录数据,多次测试后进行分析. 测试数据如图 9-10所示.
测试方法二为旋转测试,首先对测试仪器进行水平校准,然后在坡角约为8°的位置打开数据记录(采样频率50 Hz)进行原地逆时针旋转,旋转360°后停止数据记录,多次测试进行分析. 测试数据如图 11-12所示.
室外试验的测试数据如表 2所示.
行进过程中滚角最大绝对误差为2°,出现于图 9的155 s处,坡度变化率较大,由于推杆电机速度的限制,出现了较大的调平误差. 这意味着坡度变化过于剧烈的地方,例如路面较大的沟壑等,会对调平性能产生较大的不利影响. 仰角的最大绝对误差为2.77°,出现在图 10约137 s处,此时路面滚角出现了较大的瞬间变化,从而导致调平效果较差. 在旋转过程中没有突变的地面情况,调平没有明显的偏离点. 但由于传感器的波动,调平平台在旋转过程中实际角度会在一个范围内波动.
试验过程中,所设计的平台具有良好的静态调平能力,最大调平误差小于0.3°,且可以自由组合以便应对不同方向的倾斜,在较大负载情况下误差有变大的趋势. 在动态调平中,坡角突变对调平效果有较大影响,且传感器波动也会对调平效果造成影响. 本文采用的是卡尔曼滤波和姿态融合算法,后续将继续研究滤波算法和坡度变化率对调平的影响,以获得更好的调平效果. 同时,将步进电机等机械部分加强,提高平台的负载能力和动态响应能力,或在每轴的对称处加装驱动装置提高负载能力,在满足更高负载要求后,就可以作为采摘平台使用,保证登高采摘人员的安全. 由于步进电机采用脉冲控制,虽然有闭环保证定位精度,但是控制较为麻烦,完全由单片机实现插补计算量较大,且不利于扩展为多轴控制,后续将研究使用RS485,CAN等总线控制方式,扩展该平台为多轴支撑,增强其负载能力、灵活性和扩展性.
3.1. 室内试验
3.2. 室外试验
-
(1) 使用旋量理论对所提出的构型进行了自由度分析,机构运动学分析表明其自由度为2,并通过运动学逆解计算了机构位置和地面角度的关系,有效地为后续样机设计和控制提供了理论基础.
(2) 针对样机进行了制作和测试,设计了以STM32F103VET6为主控核心的调平系统,采用姿态传感器实时测量角度,并控制步进电机成功实现全向自动调平,表明了理论分析的正确性.
(3) 进行了动态和静态的两种测试,实验数据表明所设计的平台可以对地面各个方向的起伏进行有效补偿. 静态误差小于0.3°,动态误差小于3°,在丘陵山地≤15°的坡度环境有较好的自动调平效果,可以为信息采集设备提供稳定快速的采集搭载平台.



 下载:
下载: