-
开放科学(资源服务)标识码(OSID):

-
无线传感器网络(Wireless Sensor Networks,WSN)被用来跟踪目标、监测环境和捕捉环境数据,并收集一个区域内移动物体的信息[1-2]. WSN在不同应用中的成功在很大程度上取决于传感器位置,即传感器部署[3]. 无线传感器网络中的传感器由能量有限的电池供电,具有感知环境、进行有限计算、通信和移动到新地点的能力[4-5]. WSN可以修改传感器的安排,实现对目标区域的更好覆盖. 覆盖率问题是WSN中最基本的问题之一,且覆盖率是评价覆盖率优化策略的一个重要指标. 覆盖率对WSN的服务质量有重大影响,因为它直接决定WSN的监测能力[6].
既合理又有效的传感器节点部署,在降低网络成本的同时也降低了能源的使用[7]. WSN覆盖应用试图部署少量的传感器节点,以覆盖效率监测特定的目标区域. 在大多数情况下,传感器节点被随机放置在目标监测区域,导致传感器节点分布不均匀,覆盖率低[8]. 因此,通过战略性地放置传感器节点,提高WSN在监测区域的节点覆盖率至关重要. 对于大规模传感器节点部署,WSN的合理有效部署已被证明是一个NP-hard问题,找到这种情况下的最优解决方案仍然是一个难题[9].
元启发式算法被认为是处理WSN节点覆盖问题的补救措施之一. 元启发式算法可以在相当长的时间内找出接近最优的解决方案,使其成为处理WSN覆盖优化问题的便捷方法[10]. 元启发式算法是一种近似的优化算法,其解决方案可以有效解决高维优化问题. 元启发算法经常受到自然现象的启发,例如人类行为、物理感觉、动物群行为、进化概念和博弈论等[11]. 元启发式算法的设计思想受到自然现象的启发. 根据元启发式算法设计的主要灵感来源可分为5类:基于群体的算法、基于进化的算法、基于物理学的算法、基于博弈论的算法以及基于人类行为的算法.
基于群体的算法是受自然群体现象、动物、昆虫、鸟类和其他自然界生物的行为启发而开发的. 经典算法有:受鸟类和鱼类自然行为启发的粒子群优化算法(Particle Swarm Optimization,PSO)[12]、受蜂群自然行为启发的人工蜂群算法(Artificial Bee Colony Algorithm,ABC)[13]、蚁群优化算法(Ant Colony Optimization,ACO)、灰狼优化算法(Gray Wolf Optimization,GWO)[14]、受座头鲸自然行为及泡网捕猎策略启发的鲸鱼优化算法(Whale Optimization Algorithm,WOA)、帝王蝶优化算法(Monarch Butterfly Optimization,MBO)、哈里斯鹰优化算法(Harris Hawk Optimization Algorithm,HHO)、变色龙群算法(Chameleon Swarm Algorithm,CSA)和爬行动物搜索算法(Reptile Search Algorithm,RSA)等[15]. 基于进化的算法是在生物学、遗传学、自然选择法则和随机算子建模概念基础上发展起来的[16]. 基于物理学的算法介绍了数学建模的各种现象[17],模拟退火算法(Simulated Annealing,SA)是最著名的基于物理学的算法之一,其灵感来自于模拟金属退火过程. 另外还有受引力启发的万有引力算法(Gravitational Search Algorithm,CSA),受弹簧力和胡克定律启发的弹簧搜索算法(Spring Search Algorithm,SSA)和正弦余弦算法(Sine Cosine Algorithm,SCA)等.
目前,元启发算法在WNS中的研究越来越多. 杨瑞等[18]提出了基于混沌克隆遗传算法的无线传感器网络低能耗分簇方法,提升了网络能量利用效率. Tarnaris等[19]评估了遗传算法和粒子群优化在无线传感器网络的区域覆盖率和K覆盖率最大化方面的性能. 范星泽等[20]提出了改进灰狼算法的无线传感器网络覆盖优化算法,该算法使用Circle映射改进了莱维飞行策略. Deng等[21]提出一种基于牛顿力规则的虚拟弹簧力算法,该算法根据牛顿力和外部中心力的规律调整传感器之间的力,最大限度地扩大覆盖面积,同时利用中心外力填补孔洞. 李思成等[22]提出自主多决策粒子群的无线传感器网络覆盖优化算法,该算法通过引入Bernoulli混沌、Logistic混沌映射与多决策方法来改进粒子群优化,最终提高WSN的覆盖率. Lu等[23]提出了基于教学策略的改进人工蜂群算法的传感器网络感知覆盖优化算法,该算法结合了人工蜂群算法强大的全局搜索能力和教学优化快速收敛性的优点,并引入了动态搜索更新策略,用以保留人工蜂群算法中的多样性并消除参数限制. Huang等[24]为了解决无线传感器网络节点在随机部署中分布不均和覆盖率低的问题,提出了一种改进COOT鸟算法的节点覆盖优化策略.
尽管这些元启发式优化算法已经产生了许多积极的效果,但对算法性能和WSN覆盖优化仍有进一步研究的空间. 本文提出一种改进的黑猩猩优化和哈里斯鹰优化(Improved Chimp Optimization and Harris Hawk Optimization Algorithm,ICHHO)混合优化算法,将传感器放置在感兴趣的区域内. HHO是一种解决优化问题的优秀算法,存在着开发和探索之间的平衡问题. 黑猩猩优化算法(Chimpanzee Optimization Algorithm,ChOA)能够在开发和探索之间取得平衡. 然而,ChOA存在收敛性低和落入局部最小值的问题. 通过改进ChOA并将其与HHO相结合,所产生的算法有能力解决HHO或ChOA都不能解决的问题. 实验结果表明,ICHHO可以实现传感器的动态移动和位置感知,有效地优化WSN的覆盖问题.
全文HTML
-
WSN节点覆盖优化问题是每个传感器只能感知的,具有固定感知半径的已部署节点的期望放置位置,每个传感器只能在其感知半径范围内感知和发现所需的部署区域,因此每个节点必须部署在一个受限的感知半径范围内,才能实现彼此之间以及整个网络的通信. 每个节点的感知半径可以很好地满足其在可能的优化范围内寻找目标的覆盖问题.
假设WSN设置在M·Lm2的二维监测区域内,且W个传感器节点随机部署在指定位置. 为了便于计算,将部署网络的矩形区域划分为面积大小相等的M·L网格,网格中心点为监测节点w. 在最优条件下,覆盖整个监测区域且冗余感知最小的传感器数量计算为M·L·W·2Rs2. 设S为节点集合,表示为S={Sx,x=1,2,…,W},N为目标监测点集合,N={Ny,y=1,2,…,T}. Sx和Ny的坐标表示为(Sx(i),Sx(j))和(Ny(i),Ny(j)),其中x=1,2,…,W,y=1,2,…,T. 传感器节点的感知范围是一个以感知半径Rs为圆心的圆.
二维WSN监测区域的模型网络假设如下:
1) 每个传感器节点的感知半径为Rs,通信半径为Rc,均以m为单位,Rc≥2Rs.
2) 传感器节点具有正常通信功能,有足够的能量,并有时间访问数据信息.
3) 传感器节点具有相同的参数、结构和通信能力.
4) 传感器节点可以自由移动并及时更新位置信息.
无线传感器网络监控区域,当目标监测点Ny被传感器节点覆盖时,Ny与任一传感器节点之间的距离小于(等于)传感半径Rs. 传感器节点Sx与目标监测点Ny之间的欧氏距离定义为:
式(1)中,d(Sx,Ny)为节点Sx到节点Ny的距离. 如果Rs大于等于d(Sx,Ny),则目标的概率u设置为1,否则设置为0,节点感知模型设置在感知半径上. 概率公式为:
通过影响部署二维WSN监控区域的相邻节点,实现传感器节点之间的协同工作. 当任意一个目标监测点可以被多个传感器同时覆盖时,则该目标监测点Ny被成功监测到的联合概率为:
覆盖率可以定义为监控区域内所有传感器节点覆盖面积占监控区域总尺寸的比例,也即覆盖率的计算是网络部署平面二维WSN监控区域的概率之比,为:
式(4)中,CovR为WSN节点覆盖率,U(S,Ny)为目标点到达感测节点监测的概率,M·L为二维网络部署面积.
-
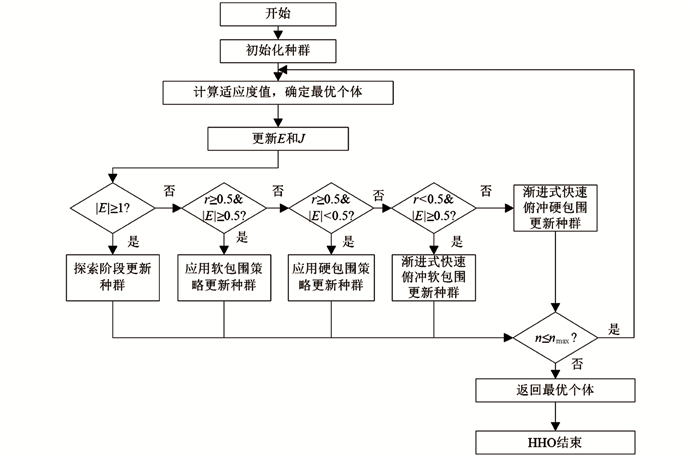
HHO是一种基于群集智能的元启发式优化算法,对于狩猎猎物主要包括开发和探索阶段(图 1). HHO的基本概念是受Harris Hawk追捕猎物机制的启发,这种机制被称为突击性扑击. 在这种机制中,它们以团队形式共同狩猎,众多鹰从不同的方向扑向猎物,试图让猎物猝不及防.
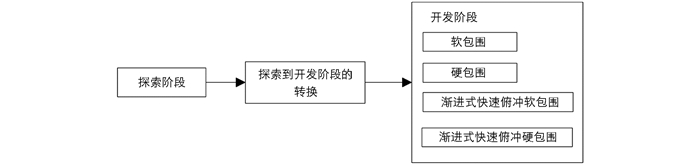
图 2中E表示兔子的逃逸能量,J为兔子逃跑过程中的跳跃距离,r表示随机变量,n表示目前的迭代,nmax是最大迭代次数. 图 2在探索阶段,哈里斯鹰随机栖息在一些地点,通过敏锐的眼睛跟踪和探测猎物,并以两种机会均等的策略进行狩猎. 在探索到开发的转换阶段,哈里斯鹰从全局搜索转向局部搜索,主要依靠逃逸能量因子来控制. 在开发阶段,哈里斯鹰找到目标猎物后会在猎物周围形成一圈围攻,等待突然袭击的机会. 然而,实际的捕食过程相当复杂,哈里斯鹰可以根据猎物行为做出必要的调整. 为了更好地模拟狩猎行为,开发阶段使用4个策略(软包围、硬包围、渐进式快速俯冲软包围和渐进式快速俯冲硬包围)进行更新,并通过能量因子和一个0~1的随机数来决定使用哪个策略.
-
黑猩猩优化算法(Chimp Optimization Algorithm,ChOA)是一种基于群体智能的启发式优化算法. ChOA基本概念受到黑猩猩追逐猎物机制和性动机的启发,旨在克服处理高维数据时收敛速度慢和陷入局部极小两个问题.
为了找到猎物,黑猩猩根据任务分工采取几种行动. 每个黑猩猩群体中有4种类型的黑猩猩:驱动者、障碍者、追逐者和攻击者. 驱动者追逐受害者,但没有试图攻击它,而树下的屏障形成了一个大坝,阻止受害者通过树枝向前移动. 追逐者必须快速移动捕捉猎物并保持有效的陷阱. 最后,攻击者作为群体领导者会预测猎物的突破路线,并利用这些信息说服猎物返回追逐者设置的陷阱. 黑猩猩狩猎机制分为两个阶段,即探索阶段和开发阶段. 探索阶段由驱动程序、障碍者和追逐者执行,而开发阶段由攻击者执行.
-
本文提出的混合优化算法,增强并融合了两种不同的优化算法:即HHO和ChOA. 两种优化算法包括两个阶段:探索阶段和开发阶段,其中探索阶段由改进的ChOA执行,开发阶段由HHO执行. 将Levy飞行应用于ChOA的探索阶段,增强了ChOA的功能,而探索阶段和开发阶段之间的选择通过猎物的逃跑能量来完成.
-
ICHHO的探索阶段采用了改进的ChOA策略,灵感来自于黑猩猩的狩猎行为. 这一阶段通过Levy飞行策略来引导黑猩猩群体,提高在解空间中的搜索效率. 本文通过调整参数来模拟黑猩猩在捕猎活动中的灵活性和不可预测性,这种动态策略逐渐减小了特定参数的影响,从而创造了一个适应性强、灵活性大的搜索过程.
-
本文算法的一个关键方面是在探索和开发阶段之间做出战略选择. 这个决策体现了在黑猩猩行为过程中观察到的适应机制. 该算法评估了“兔子”(类似于狩猎场景中的猎物)的逃逸能量,并通过引入适应性参数来调整逃逸能量. 这种逃逸能量受到随机因素和当前迭代的影响,决定算法是侧重于探索还是开发. 这种智能选择保证了算法在全面探索搜索空间和充分利用有前景区域之间取得平衡. 因此,这个自适应机制是算法成功平衡探索阶段和开发阶段的关键.
-
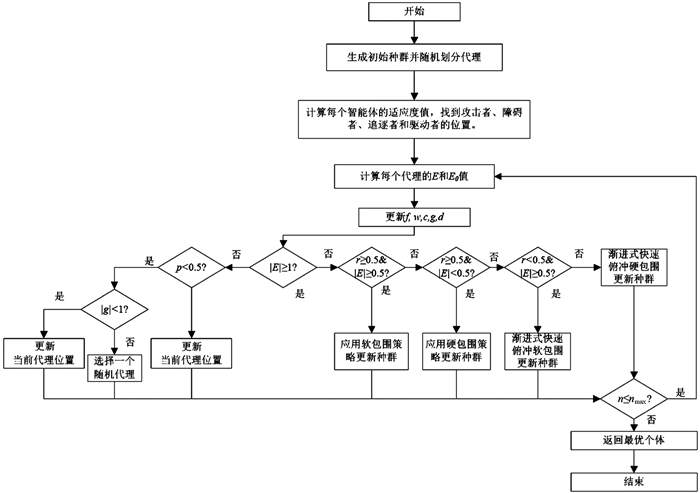
在HHO的开发阶段,运用4种策略来有效地反映实际情况. 为了检测猎物是否成功逃离,使用了随机变量(r). r<0.5表示成功逃离,r≥0.5表示逃离失败. 哈里斯鹰的行为受猎物逃跑能量的影响. 如果|E|≥0.5,则发生软包围;如果|E|<0.5,则发生硬包围. 本文算法ICHHO的伪代码显示在算法1中,对每个个体的处理过程包括更新能量、探索阶段和开发阶段的位置更新、以及最终的参数更新和适应度计算. 整个算法在最大迭代次数nmax内循环执行,以便找到最优个体,其流程如图 3所示.
算法1:ICHHO算法伪代码 注:黑猩猩的新位置将根据受害者位置、距离和参数进行更新,以便继续寻找猎物;或采用混沌值,进入探索阶段,以便进行更广泛的搜索. 初始化种群大小和最大迭代次数; 初始化智能群体位置; 初始化f,c,w,g和d(其中,f是控制猎物逃脱能量的因子,用于计算猎物的逃脱能量;c,w,g和d是更新黑猩猩群体位置的参数.) 计算适应度 选择攻击者、障碍者、追逐者和驱动者 While n<nmax For each agent 更新初始能量E0和E If (|E|≥1) then //探索阶段 If p<0.5 If |g|<1 更新当前黑猩猩的位置 Else If |g|>1 选择一个随机搜索agent End If Else If p≥ 0.5 更新当前黑猩猩的位置 End If Else If (|E|<1) then //开发阶段 If (r≥0.5 and |E|≥0.5) then 使用软包围更新种群位置 Else If(r≥0.5 and |E|<0.5) then 使用硬包围更新种群位置 Else If(r<0.5 and |E|≥0.5) then 使用渐进式快速俯冲软包围更新种群位置 Else If(r<0.5 and |E|<0.5) then 使用渐进式快速俯冲软硬包围更新种群位置 End If End For 更新f,c,w,g和d 计算所有agents的适应度 更新黑猩猩的位置 n=n+1 End While Return最优个体 在随机位置初始化agent,并计算每个agent的适应度. 根据修正后的猎物逃脱能量,选择开发阶段和探索阶段;如果猎物的逃脱能量值大于1,则利用基于回声回波的探索阶段来寻找猎物,如果猎物的逃脱能量值低于1,则利用开发阶段到达预定位置. 开发阶段主要由4种HHO策略组成,即软包围、硬包围、软包围+渐进快速俯冲和硬包围+渐进快速俯冲. 所使用策略的选择基于两个因素,即决定逃跑成功或失败的逃跑值和猎物的逃跑能量. 计算代理的新位置,并进行处理直到满足停止条件为止. 攻击黑猩猩的位置代表了优化问题的最佳解.
-
ICHHO算法的计算复杂度取决于ChOA和HHO的个体复杂度. 任何优化算法的计算复杂度取决于3个操作:算法初始化、适应度函数计算和种群位置更新. 对于初始化过程,复杂度为O(N),其中T为总体大小(解的个数). 对于适应度函数,其复杂度仅取决于问题本身,因此无法对其进行假设. 对于位置更新,复杂度取决于3个因素,即种群大小(T)、总迭代次数(nmax)和问题的维度(dim). 位置更新的复杂度可以用O(nmax×T)+O(nmax×T×dim)来计算. 因此,ChOA和HHO的计算复杂度均为O(N)+O(nmax×T)+O(nmax×T×dim)=O(N(1+nmax+nmax×dim)). 对于本文提出的混合算法ICHHO,计算复杂度为O(T)+O(2×nmax×T)+O(2×nmax×T×dim)=O(N(1+2×nmax+2×nmax×dim)).
-
为黑猩猩和哈里斯鹰寻找最优狩猎过程类似于获得传感器最佳覆盖范围的过程,而最优个体位置代表传感器覆盖的坐标. 在保持有效通信的同时,使用相同数量的传感器覆盖更大的区域是基于ICHHO的WSN优化覆盖目标.
步骤1:输入WSN要检测的区域大小、传感器数量、传感半径、通信半径及ICHHO算法的设置;
步骤2:初始化总体,其中每个个体代表一个覆盖方案. 在此步骤中,传感器随机分布在监测区域周围,利用覆盖率函数确定初始覆盖;
步骤3:更新黑猩猩和哈里斯鹰的位置信息,计算相应的适应程度. 根据式(4)更新覆盖率,找到最优传感器位置;
步骤4:如果条件满足,立即退出循环. 输出传感器的最佳覆盖方案.
2.1. HHO
2.2. ChOA
2.3. ICHHO
2.3.1. 基于改进ChOA的探索阶段
2.3.2. 探索阶段和开发阶段之间的选择
2.3.3. 使用HHO的开发阶段
2.3.4. 算法复杂度
2.4. 基于ICHHO算法的覆盖优化设计
-
本次模拟测试的环境为Windows 10专业版,64位操作系统,Intel(R) Core (TM) i5-4210H CPU @2.90 GHz,8GB. 仿真软件为MATLAB 2016a.
假设WSN传感器节点部署在W·L方形监控区域的场景可设置为部署区域,如40 m×40 m,80 m×80 m,100 m×100 m,160 m×160 m. 表 1列出了WSN节点部署区域的实验参数. 传感器节点的感知半径RS设为10 m,通信半径RC设为20 m,传感器节点数为w,分别为20,40,50,60个传感器节点. Iter表示迭代次数,可以分别设置为500,1 000和1 500.
将ICHHO的最优结果与选择的SSA,PSO,GWO,SCA,HHO等方案进行WSN节点部署覆盖优化,验证了该算法的良好性能. 表 2比较了ICHHO方法与其他策略SSA,PSO,GWO,SCA和HHO算法在百分比覆盖率、收敛迭代和监控区域大小方面的优势.
-
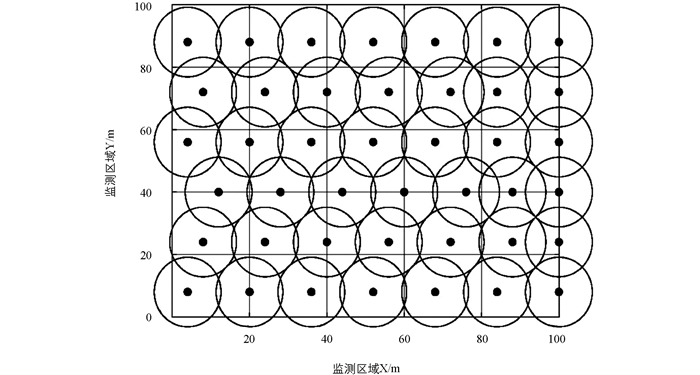
传感器最初随机覆盖在监控区域,随着ICHHO的优化,重叠传感器开始减少(图 4),且在监测区域内分布均匀.
从表 2可以看出,初始覆盖率为79.26%,ICHHO优化后覆盖率达到97.73%,提高了18.47%. 一开始,区域中冗余传感器较多,区域能量空洞较明显,显得杂乱. 算法优化后,传感器分布明显均匀,覆盖比明显提高. 结果表明,ICHHO对无线传感器网络的覆盖优化有效.
-
表 3从百分比覆盖率、收敛迭代和监测区域大小等方面将ICHHO算法与其他算法进行比较.
由表 3和图 5可以看出,ICHHO的覆盖率最高,其优化结果最好. 实验结果证明,在解决WSN覆盖优化问题上,ICHHO显示出比HHO算法更好的结果,它的表现也优于其他4种算法. ICHHO方案在覆盖区域内产生了最佳的全局解决方案,具有较高的覆盖率,覆盖了节点的整个空间区域. 尽管SSA,GWO,PSO,CSA与ICHHO一样都是基于群体的元启发式算法,但ICHHO在所有样本中都获得了最高的覆盖率,这一优势是由ICHHO将ChOA和HHO开发与探索阶段进行结合,既解决了ChOA容易出现收敛缓慢和陷入局部最小值的情况,又增强了优化算法在探索和开发阶段之间取得平衡能力所致. 该混合优化算法引导传感器节点到达它们的最佳位置.
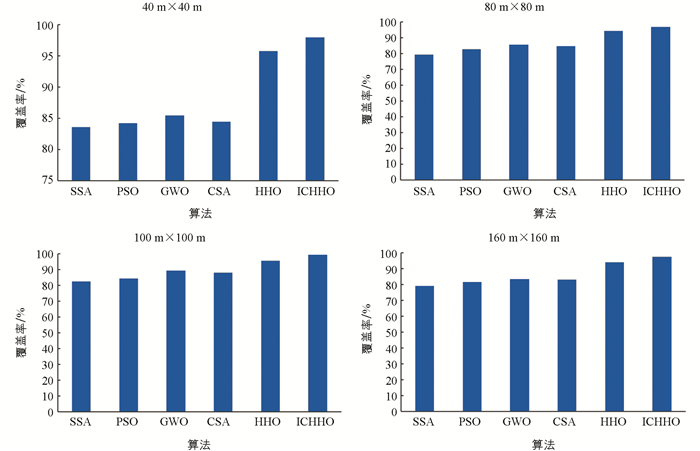
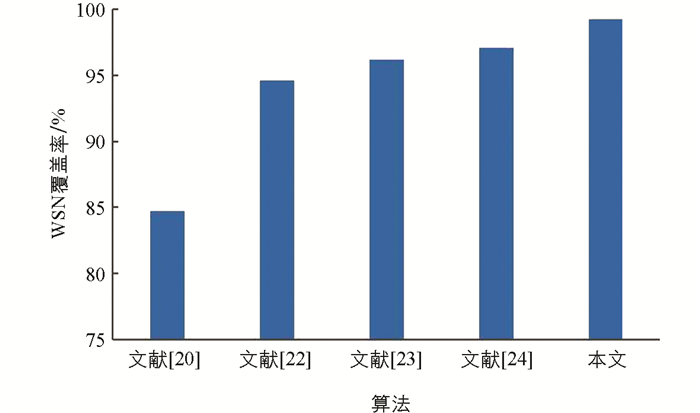
为了进一步验证ICHHO在优化传感器覆盖方面的优越性,将ICHHO与4种改进的优化算法进行了比较,结果如图 6所示. 在相同的参数值下,ICHHO提高了WSN的覆盖率.
3.1. 算法有效性对比
3.2. 算法有效性对比
-
本文提出了一种改进的ICHHO算法,解决无线传感器网络节点在随机部署中的不均匀分布和低覆盖率问题. ICHHO通过在HHO探索阶段引入改进ChOA来避免原HHO和ChOA的缺点,如收敛速度慢,在处理复杂情况时容易陷入局部极值等. 最佳节点覆盖率的目标函数,是通过测量每个传感器节点的传感半径和部署WSN时的通信能力来计算节点之间距离而建立的数学模型. 本文使用了其他多种优化算法对WSN节点最优覆盖率进行实验,结果表明ICHHO实现了最佳的传感器覆盖,优于其他算法. 通过ICHHO最终解决了WSN的覆盖问题,优化了传感器覆盖范围并增强了传感器连通性. 未来将进一步完善ICHHO算法,深入研究其在大规模、复杂WSN网络中的性能表现. 同时,通过应用实验结合实际工程场景,验证算法的可行性和有效性,并探索其在特定场景下的优化效果和应用价值.



 下载:
下载: