-
开放科学(资源服务)标识码(OSID):

-
自动机械式变速器(AMT)因结构简单、传动效率高、成本低等优势被广泛用于纯电动汽车领域. 搭载AMT,不仅能降低设计阶段整车对驱动电机工作扭矩的要求,而且合理的换挡规律还能调节驱动电机工作区域,使其在高效区域工作的同时也能满足整车驱动扭矩. 因此,换挡规律的合理制定成为AMT纯电动汽车性能提升的有效途径之一[1-2].
目前,国内外研究人员对AMT换挡规律已开展了丰富的研究. 根据换挡参数的不同,传统换挡规律可分为单参数换挡规律、双参数换挡规律以及三参数换挡规律[3-4]. 其中,以车速和加速踏板开度作为控制参数的双参数策略应用较为广泛. Zhu等[5]基于电机效率MAP图,分别提出了以动力性和经济性为目标的换挡规律设计方法,并通过台架试验验证了方法的有效性. 通过该方法获得的2种换挡规律在实际应用时需通过一定的规则对策略进行切换. Wang等[6]设计了一种基于功率的换挡规律,在满足车辆功率需求的前提下,使驱动电机尽可能在高效区工作,仿真结果表明该策略具有较好的动力性,其能耗与经济性换挡规律相比也有所降低. Sun等[7]根据驱动电机负载情况对动力性换挡规律和经济性换挡规律进行切换,设计了一种综合性换挡规律,并通过ADVISOR平台验证了综合性规律的有效性. 陈淑江等[8]分析了2挡AMT纯电动汽车动力性与经济性换挡规律下的能耗特性,根据车辆不同负荷区间制定出兼顾动力性与经济性的综合换挡规律,并通过仿真进行了验证. 上述策略能够在满足车辆动力性的基础上得到较理想的经济性. 为进一步提升经济性,刘文光等[9]分析了电池、电机和变速器效率随换挡参数的变化,以驱动系统效率最高为目标设计了最佳经济性换挡规律,以不同挡位加速度最大为目标设计了最佳动力性换挡规律,并基于模糊理论设计了根据动力因数需求切换的换挡策略,较好地改善了整车电耗,延长了续航里程. 张东东等[10]以百公里加速时间和单位里程能耗作为优化目标,通过多目标优化算法优化换挡车速,以电机效率最优作为换挡点选取条件,获取了考虑综合性能的最佳换挡规律,并通过仿真验证了换挡规律的性能. 高玮等[11]以能耗最低为优化目标,采用动态规划方法获取了纯电动公交的最优换挡工作点,提取了可用于实车控制的双参数换挡规律,并通过仿真分析验证了策略的节能效果. Zhao等[12]也通过动态规划对矿用卡车的换挡规律进行了优化,所获取的最佳换挡策略能够有效提升车辆的经济性.
考虑动态规划求解最佳换挡点后,如何提取最佳换挡规律成为学者关注的重点. 靳光盈等[13]采用动态规划对标准工况下车辆的挡位切换序列进行优化,提出了一种基于聚类方法的换挡规律提取方法,并通过仿真验证了所提取换挡规律的有效性. Lin等[14]通过动态规划离线获取了车辆全局最优工作点,并基于k-均值聚类提出一种AMT换挡规律的获取方法,对比结果表明所提出方法在经济性方面有较大优势,换挡次数也较为理想. 由于车辆行驶过程中,动力性与经济性存在一定矛盾,因此,制定换挡规律过程中,如何同时考虑动力性与经济性之间的协调也显得尤为重要. Saini等[15]将遗传算法应用到换挡规律优化过程中,将动力性与经济性作为多目标问题考虑,得到了最佳换挡策略. 宋强等[16]也采用同样方法建立了兼顾经济性和动力性的综合换挡规律优化模型,将整车能耗与换挡点加速度差值之和作为优化目标进行优化,结果表明综合换挡规律能够在满足整车动力性的同时获得优异的经济性. 上述方法均为离线优化方法,所获取的基于规则的换挡规律与在线实时工况的适应性有待研究. 为解决车辆规则型换挡规律工况适应性差的问题,Ma等[17]在考虑最优功率及经济性换挡的前提下,建立了一种基于模糊控制的换挡规律,仿真结果表明优化后的换挡规律不但具有较好的动力性,经济性也得到了一定提升. 殷学冰等[18]通过遗传算法得到了基于动力性与经济性的2DCT综合型换挡规律,并引入加速度构建了三参数模糊控制器用于换挡规律的在线调整,满足动力性与经济性的同时有效降低了换挡频率. Guo等[19]将模型预测控制算法用于车辆控制,以改善车辆经济性并降低AMT换挡频率,结果表明该方法有效降低了车辆能耗并抑制了AMT频繁换挡. 此外,雷雨龙等[20]通过马尔可夫链对行驶工况进行预测,并采用贪心策略优化了电动车AMT换挡点,有效提升了车辆在特定工况下的经济性. Lin等[21]基于LVQ神经网络提出了一种基于动力修正因子的换挡策略自适应调整方法,结果表明该方法与传统换挡规律相比具有较好的节能效果,并且对不同行驶工况具有良好的适应性.
综上所述,现阶段对AMT纯电动汽车换挡规律的研究多集中于换挡点优化方面,方法以电机效率法、动态规划法、遗传算法以及预测型控制为主,上述方法多以已知工况作为输入条件,其在线实时性仍有待验证. 因此,在满足车辆动力性与经济性的需求下,提升换挡规律对行驶工况的自适应能力对于换挡规律的实时应用尤为重要. 鉴于此,本文提出了一种基于多目标粒子群与模糊控制的多挡AMT纯电动城市客车自适应换挡规律设计方法,通过实际运行工况对换挡规律进行了多目标优化,并采用模糊控制对换挡点进行了在线自适应调整,最后在实际道路工况下完成了该策略的验证.
全文HTML
-
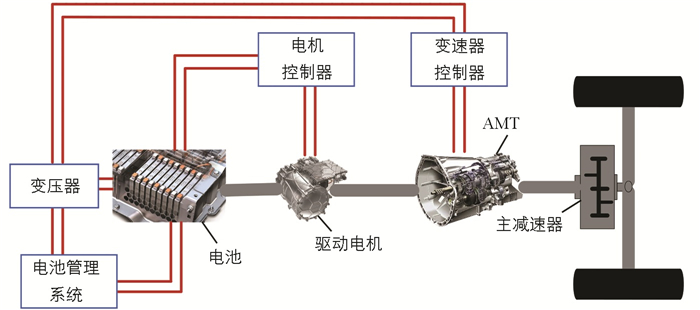
本文基于配备3挡自动变速器的纯电动客车开展研究,车辆动力系统主要包括动力电池、驱动电机、AMT、主减速器等,具体架构如图 1所示.
驱动电机与AMT变速箱直接连接,并通过动力电池提供的能量驱动车辆行驶,驱动电机在车辆制动过程中也可回收能量. 纯电动客车整车参数及性能要求如表 1所示.
-
由于驱动电机具有驱动车辆行驶并回收制动能量的功能,其输出功率表示如下:
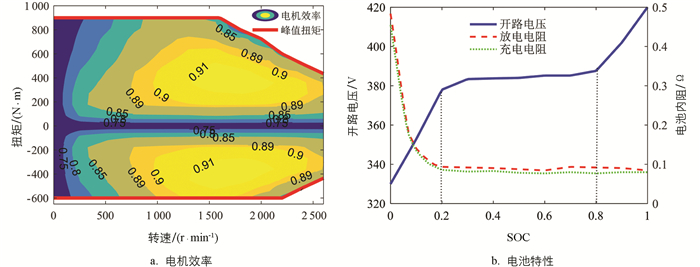
式中:Pm表示电机输出功率;nm与Tm分别表示电机工作转速与转矩;sgn(·)为符号函数;ηm为电机效率,可通过台架试验获取. 此外,考虑纯电动汽车制动能量回收对能耗有一定影响,本文采用电机最大回馈策略实现车辆制动能量回收[2]. 为避免制动扭矩过大对电机造成损害,将电机最大制动扭矩限制为600 N·m. 因此,本文采用的电机效率特性如图 2(a)所示.
-
纯电动客车采用磷酸铁锂电池作为能量源,电池容量为360 A·h,额定电压为384 V. 忽略温度对电池寿命及充放电影响,将电池模型简化为等效内阻模型[22],电池负载功率可表示为:
式中:Pbat表示电池负载功率;Voc表示电池开路电压;Ibat表示电池电流;Rbat表示电池内阻. 式(2)可改写成如下形式:
因此,动力电池动态模型可由式(4)表示:
式中:Q0表示电池容量;Soc为电池荷电状态(Sate of Charge,SOC),其与电池开路电压及电池内阻的动态关系可通过试验获取. 本文采用的动力电池的特性曲线如图 2(b)所示.
-
文中纯电动客车采用3挡AMT来改善电机工作区以降低能耗,AMT模型可表示为:
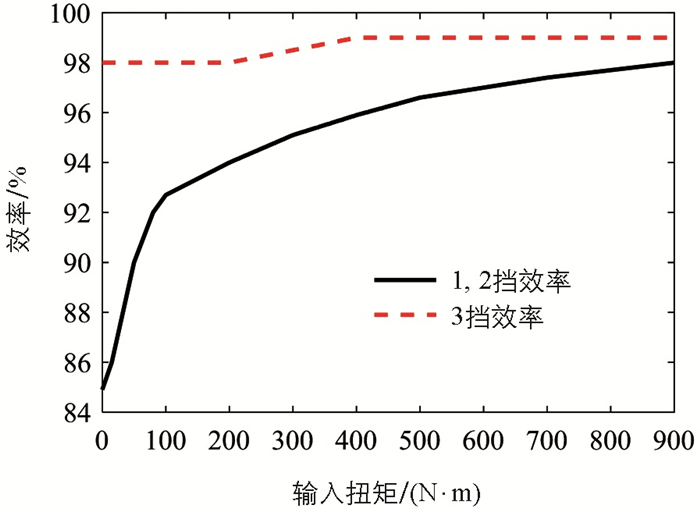
式中:Tb_out与nb_out分别表示AMT输出轴转矩与转速;ig(n)表示变速器第n挡的速比,本文中n=1,2,3;ηg(n)为AMT传动效率,可由台架试验获取,结果如图 3所示.
-
忽略横向动力学影响,将车辆纵向动力学模型简化为质点模型:
式中:k表示时刻;m表示整车质量;δ表示车辆旋转质量换算系数;v、Ft、Ff、Fw、Fα分别表示车辆行驶速度及所需驱动力、滚动阻力、空气阻力以及坡度阻力,可由下式表示:
式中:g为重力加速度;f为滚动阻力系数;α为坡度角;Cd为风阻系数;A为迎风面积;ρ为空气密度;ig、i0分别表示变速箱速比与主减速比;r为滚动半径;ηT为主减速器传动效率.
1.1. 驱动电机模型
1.2. 动力电池模型
1.3. AMT模型
1.4. 车辆动力学模型
-
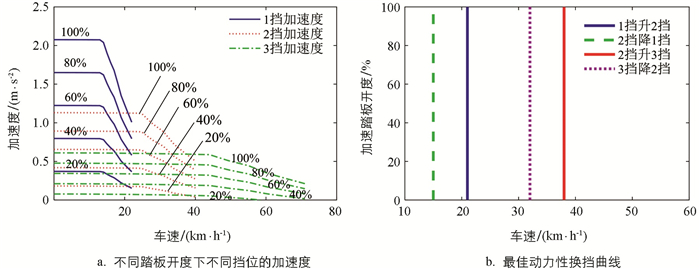
最佳动力性换挡规律是指在充分发挥驱动电机性能的前提下,在行驶过程中换挡点能够满足最佳动力性的要求. 本文采用最大加速度法来设计最佳动力性换挡点:即在同一踏板开度下,当后一挡的加速度与前一挡的加速度有交点时进行升挡,如图 4(a)所示. 为了避免循环换挡,降挡线与升挡线之间的间隔为5~8 km/h [2],结合图 4(a)可求得最佳动力性换挡规律曲线,如图 4(b)所示.
-
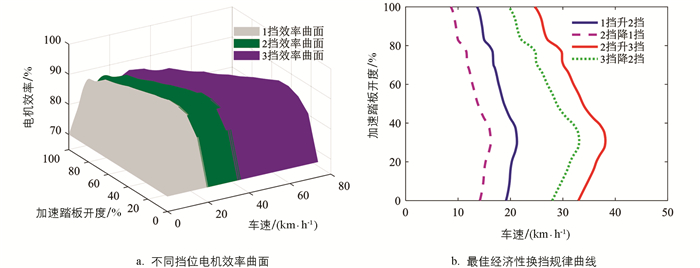
在经济性能方面的主要影响因素是电机效率,因此为了改善纯电动客车的经济性,使能量利用率得到提高,最佳经济性换挡规律的制定就是让电机尽可能地在高效率区工作. 因此,取相邻挡位电机效率曲面的交线即可得到最佳经济性换挡规律的升挡曲线,如图 5(a)所示. 与最佳动力性换挡规律相类似,降挡线与升挡线之间的速度差取5~8 km/h [2],则得到的最佳经济性换挡规律如图 5(b)所示.
2.1. 最佳动力性换挡规律
2.2. 最佳经济性换挡规律
-
换挡规律制定时,经济性与动力性目标存在相互制约关系,动力性规律要求车辆换挡尽可能晚,而经济性规律则相反,为了同时兼顾两种性能,需要同时考虑换挡车速对二者的影响,因此在设计过程中首先通过多目标粒子群算法对换挡规律进行综合优化.
-
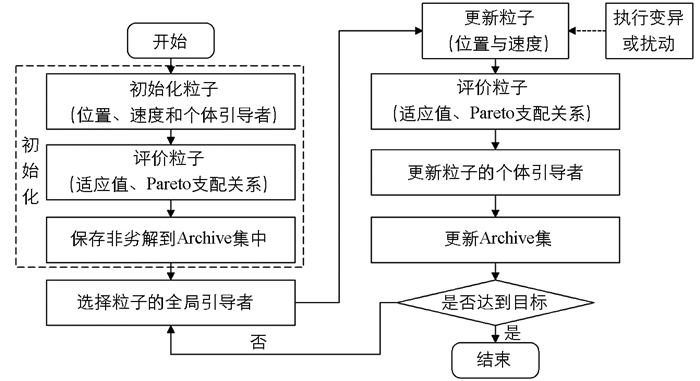
MOPSO算法是在基础粒子群算法中引入Pareto支配形成的. 在粒子活动过程中,每个粒子的最优位置存储于Archive集中以避免最优粒子在更新过程中的丢失. 此外,得到的非劣解与Archive集将重新组合并通过Pareto支配关系排序,得到新的Archive集,进而通过群个体最优解得到全局最优解[23]. 其算法流程如图 6所示.
-
目标函数包含动力性目标函数和经济性目标函数. 在优化过程中,求目标函数的最小值,即:
其中,动力性目标函数根据加速时间来确定[16],将车辆从起步加速到某一车速时所用的时间作为动力性目标函数,如下式所示:
式中:v1、v2为车辆行驶时的换挡点;δ1、δ2、δ3分别为不同挡位下的旋转质量系数;目标车速为50 km/h.
将车辆在加速过程中的能耗作为经济性目标函数,表示为:
式中:t1与t2分别为车辆在1、2挡运行的时间,t3为车辆运行的总时间.
为提高优化效率,优化过程中对换挡车速分别进行了约束,表达式如下:
式中:v1_d、v2_d表示最佳动力性换挡规律下1挡升2挡时的车速与2挡升3挡时的车速. v1_e、v2_e表示最佳经济性换挡规律下1挡升2挡时的车速与2挡升3挡时的车速.
-
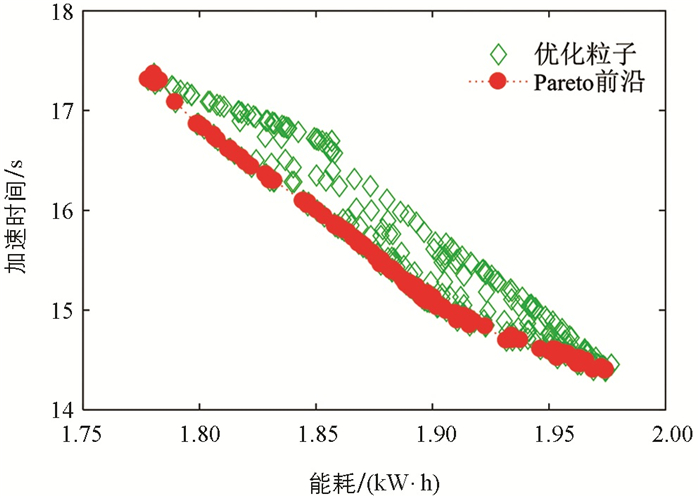
求解过程中,最大迭代次数为500,粒子群规模为100,求解得到的100%踏板开度下的最优解集及Pareto前沿如图 7所示.
由于动力性与经济性评价指标的量纲不同,求解最优结果时通过线性加权对2个评价指标进行了综合[24],如下式所示:
式中:ω1与ω2为权重因子,s1与s2为比例因子. 计算过程中,ω1与ω2,s1与s2根据不同踏板开度下f1与f2的数量级进行选取,其中ω1+ω2=1.
将优化变量v1与v2分别在加速踏板开度为10%、20%、30%、40%、50%、60%、70%、80%、90%、100%下进行优化,通过MOPSO算法得到的最终结果如表 2所示.
-
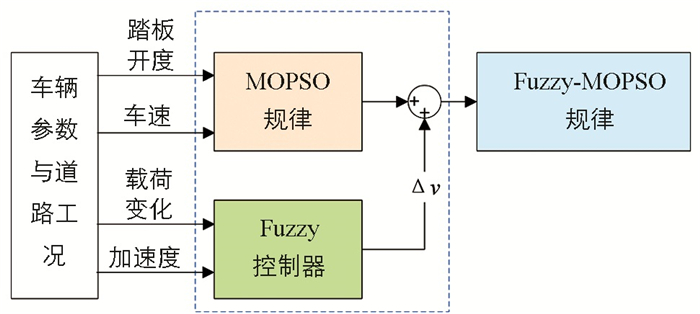
通过MOPSO算法得到的换挡规律基于车辆加速工况设计,未考虑实际道路工况特征以及车辆自身状态的变化,其自适应能力较差. 为提高换挡规律对行驶工况及车辆自身状态的适应能力,以载荷变化与加速度为输入参数,通过模糊控制对换挡点进行动态调整,其流程如图 8所示.
-
以实际工况下城市客车加速度与载荷变化作为模糊控制器输入,换挡点速度调整量作为模糊控制器输出. 考虑城市客车实际工作情况,加速度范围a=-6~6 m/s2,载荷变化Δm=0~5 000 kg,车速调整量Δv=-6~6 km/h.
-
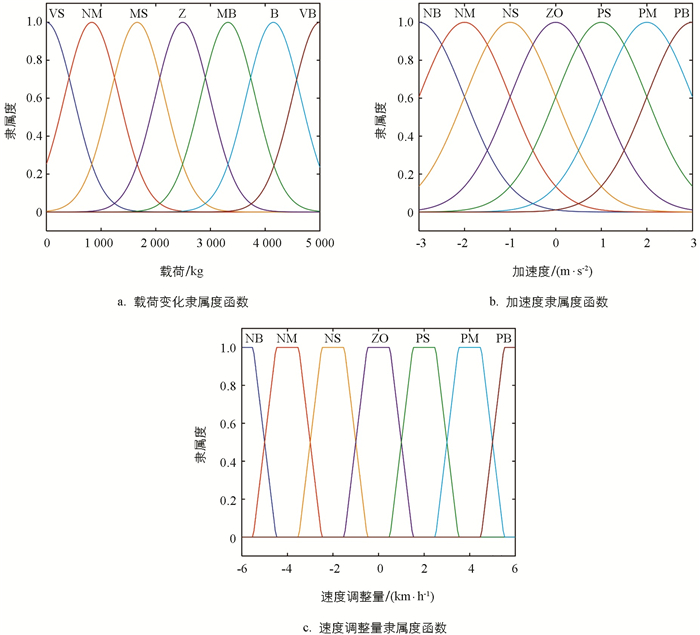
分别将加速度、载荷变化与速度调整量转化为论域{-3,-2,-1,0,1,2,3}、{0,1 000,2 000,3 000,4 000,5 000}和{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}. 将载荷变化Δm的模糊子集划分为:VS(极小)、NM(小)、MS(较小)、Z(中)、MB(较大)、B(大)、VB(极大). 将加速度a的模糊子集划分为:NB(负大)、NM(负中)、NS(负小)、ZO(中)、PS(正小)、PM(正中)、PB(正大). 将车速调整量Δv的模糊子集划分为:NB(负大)、NM(负中)、NS(负小)、ZO(中)、PS(正小)、PM(正中)、PB(正大). 则模糊控制器的输入与输出隶属度函数如图 9(a)~9(c)所示.
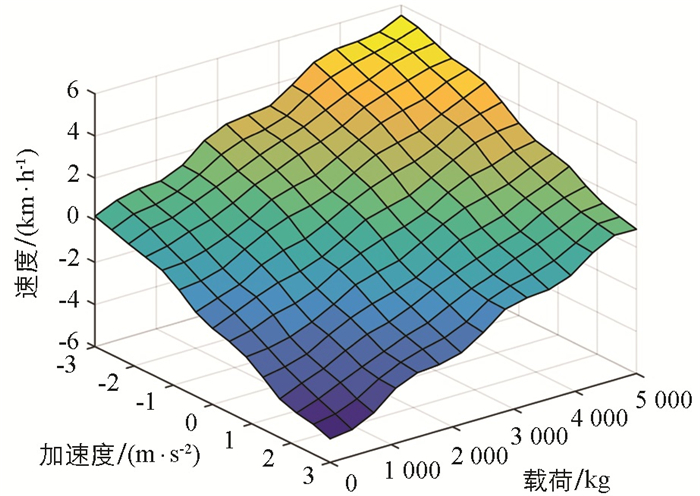
本文中,模糊控制输入参数为2个,各有7个子集,共能获取7×7=49条控制规则. 考虑实际运行过程中,车辆加速度越大,换入高挡的趋势越明显,可提前换挡;而车辆载荷增加将提高对整车动力性的需求,需延迟换挡. 因此,换挡速度调整量Δv的输出依据为:载荷越大调整量越大;加速度越大调整量越小. 根据模糊规则得到的载荷和加速度与换挡速度调整量的关系如图 10所示. 最终,将基于载荷与加速度的模糊控制器引入MOPSO算法所得的换挡车速进行在线自适应调整,即可得到Fuzzy-MOPSO换挡规律.
3.1. 基于多目标粒子群算法的优化
3.1.1. 多目标粒子群优化算法(MOPSO)
3.1.2. 优化目标及约束
3.1.3. 优化结果
3.2. 换挡规律自适应设计
3.2.1. 模糊控制规律的输入与输出
3.2.2. 模糊控制器设计
-
为了验证Fuzzy-MOPSO换挡规律的性能,分别对不同换挡规律开展动力性与经济性验证.
-
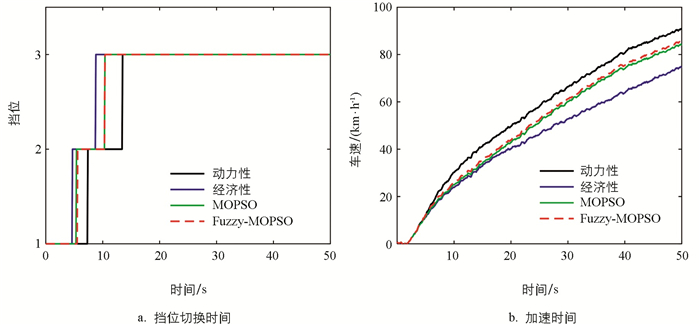
考虑到汽车动力性3个评价指标中,加速时间常用来评价不同换挡规律的动力性能,本文在加速踏板开度为100%的情况下分别对动力性、经济性、MOPSO、Fuzzy-MOPSO 4种换挡规律进行了加速性能验证,其结果如图 11所示.
由图 11(a)可知,4种换挡规律下其换挡时间存在一定差异. 其中,经济性规律挡位切换时间最早,在车辆启动后4.6 s升入2挡,并在8.7 s时升入3挡;动力性换挡规律挡位切换时间最晚,7.1 s时升入2挡,13.4 s时升入3挡行驶. 由于MOPSO规律与Fuzzy-MOPSO规律兼顾了车辆动力性与经济性,因此,挡位切换时间均介于动力性与经济性规律之间. 此外,由于Fuzzy-MOPSO规律考虑了车辆载荷的变化,挡位切换时间略晚于MOPSO规律. MOPSO规律与Fuzzy-MOPSO规律升入2挡的时间分别为5.1 s与5.2 s,差距较小;升入3挡的时间分别为9.8 s与10.4 s.
车辆升挡时间的提前必然导致加速性能的损失. 由图 11(b)可知,经济性规律的加速性能最差,动力性规律的加速性最好,MOPSO规律与Fuzzy-MOPSO规律介于动力性规律与经济性规律二者之间. 由于Fuzzy-MOPSO规律充分考虑了车辆载荷与加速度的变化,因此,动力性能略高于MOPSO规律.
表 3给出了不同换挡规律下车辆0-50 km/s加速时间,通过比较可知MOPSO规律比经济性规律加速时间减少了11.7%,Fuzzy-MOPSO规律比经济性规律加速时间减少了15.3%. 相比而言,Fuzzy-MOPSO比MOPSO规律的加速时间减少了4.1%,其动力性能更好.
-
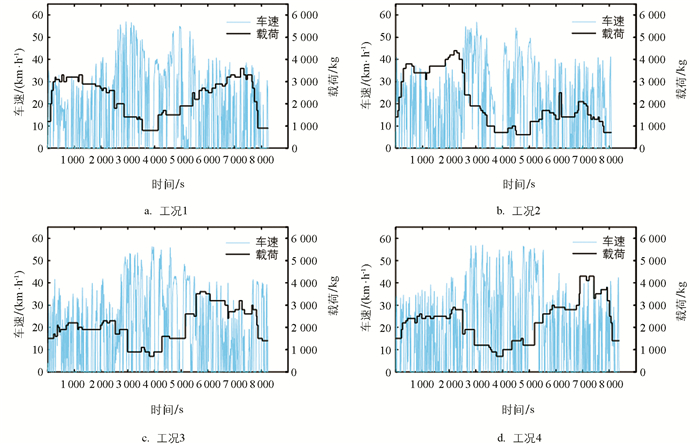
为验证不同换挡规律的经济性,在实际道路工况下对4种换挡规律的经济性进行了比较. 此外,分析中还考虑了不同换挡规律的换挡频率. 在基于实际道路工况的验证过程中,选取了某公交线路的4段城市道路随机工况,并采集了该线路实际乘客载荷变化情况,所采用的含车速与载荷的实际道路工况如图 12所示.
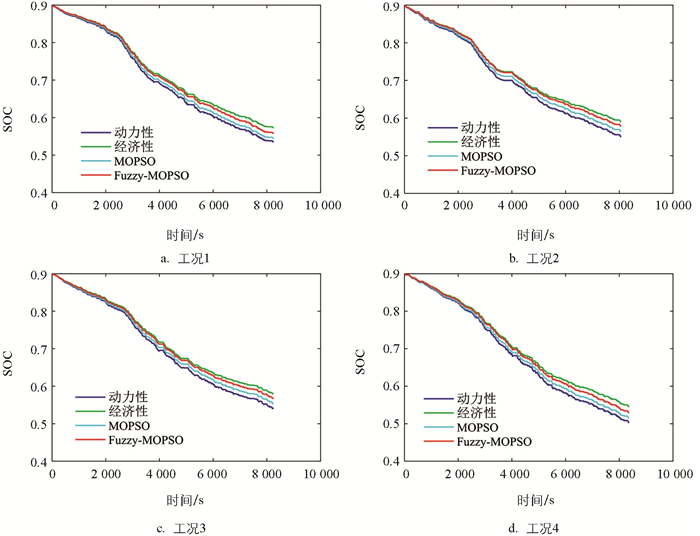
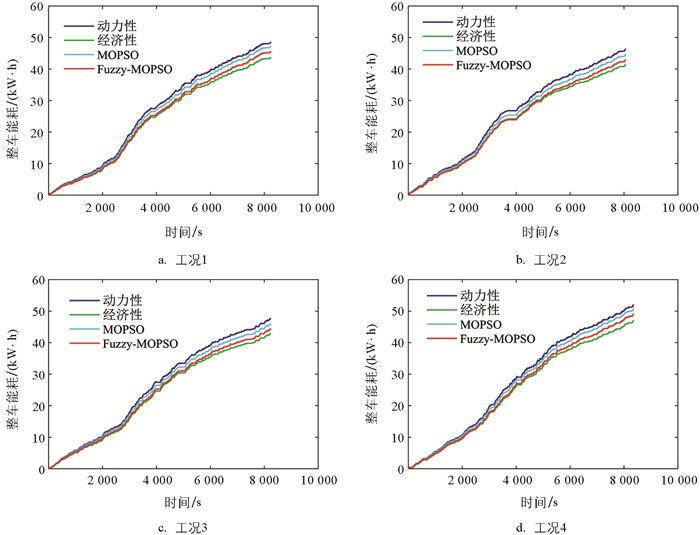
图 13与图 14分别为基于4段实际道路工况所得到的4种不同换挡规律的SOC变化曲线与整车能耗变化曲线. SOC变化方面,动力性规律下降最快,经济性规律下降最慢;MOPSO规律介于动力性规律与经济性规律之间,Fuzzy-MOPSO规律较MOPSO规律下降更缓慢. 相应地,整车能耗方面,动力性规律能耗最高,经济性规律最低,MOPSO能够兼顾车辆动力性与经济性,其能耗位于动力性规律与经济性规律之间. 相比于MOPSO规律,Fuzzy-MOPSO规律在整车能耗方面的表现更为优越.
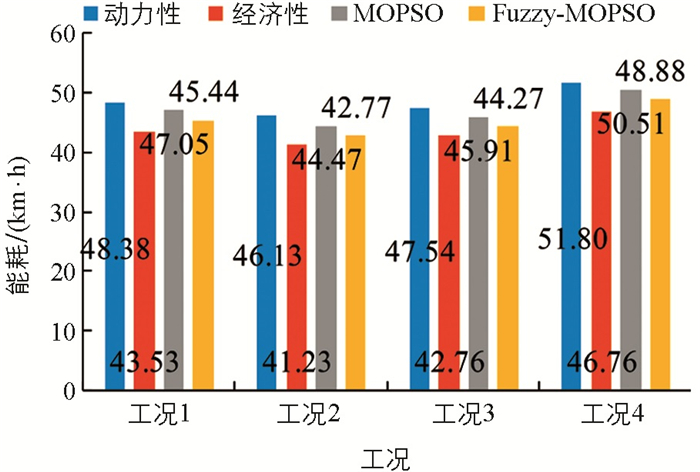
图 15为4段实际道路工况下,4种换挡规律的能耗统计图. 由图 15可知,4段工况下,MOPSO规律与动力性规律相比,能耗分别降低了2.75%、3.6%、3.43%、2.49%;Fuzzy-MOPSO规律与动力性规律相比,能耗分别降低了6.08%、7.28%、6.88%、5.63%. 因此,Fuzzy-MOPSO规律与MOPSO规律相比,在兼顾动力性的基础上,其节能性更优越.
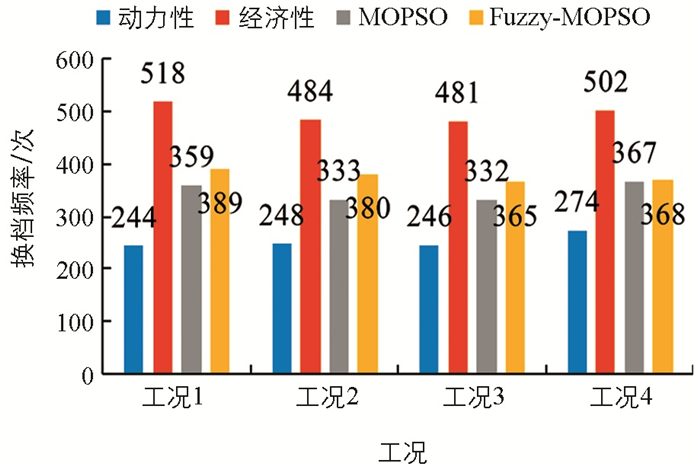
换挡频率升高会引起挡位频繁切换,导致AMT使用寿命降低. 图 16统计了4种换挡规律在4段实际道路工况下的换挡频率. 由图 16可知,动力性规律的换挡频率最低,经济性规律的换挡频率较高. MOPSO规律的换挡频率接近于动力性规律,与动力性规律相比分别增加了155次、85次、86次、93次. 尽管Fuzzy-MOPSO规律的换挡频率较MOPSO规律有所增加,分别增加了30次、47次、33次、1次,但是其节能效果较MOPSO规律更好,综合性能较高.
4.1. 动力性分析
4.2. 经济性分析
-
本文以3挡AMT纯电动客车为研究对象,开展了基于多目标粒子群与模糊控制的自适应换挡规律研究,主要工作与结论总结如下:
1) 构建了基于动力性目标与经济性目标的双参数最佳动力性与最佳经济性换挡规律.
2) 基于多目标粒子群算法对换挡规律进行了多目标优化,得到了同时考虑动力性与经济性的MOPSO换挡规律.
3) 考虑城市公交载荷及加速度变化,建立了基于模糊控制的Fuzzy-MOPSO自适应换挡规律,提升了换挡规律对随机工况的适应能力.
4) 对4种换挡规律开展了动力性验证,并基于实际道路工况开展了经济性验证. 结果表明,Fuzzy-MOPSO规律具有较好的加速性能,0-50 km/h加速时间比经济性换挡规律减少了15.3%,加速性能与MOPSO规律相比,提升了4.1%. 能耗方面,4段实际道路工况下,Fuzzy-MOPSO规律的能耗比动力性规律分别降低了6.08%、7.28%、6.88%、5.63%,与MOPSO规律相比,节能潜力更大. 此外,Fuzzy-MOPSO规律在实际道路工况下的换挡频率与MOPSO规律相当,均接近于动力性规律.



 下载:
下载: