-
开放科学(资源服务)标识码(OSID):

-
随着互联网和智能手机的普及,社交网络已经成为现代社会中人们日常生活和工作的重要组成部分. 而社交网络中信息传播迅速,影响力巨大,关键节点在信息传播过程中发挥着重要作用. 对于社交网络中重要信息传播的研究,挖掘重叠节点具有重要的理论和实际价值. 特别是在信息传播和舆情监控等领域,重叠节点的挖掘可以帮助人们更好地理解信息是如何在社交网络中扩散,以及如何更有效地监控和管理这些传播过程.
社交网络信息传播是指信息在社交网络中的扩散过程[1]. 随着社交网络的普及和快速发展,信息传播研究逐渐成为学术界和产业界关注的焦点. 在这一领域的研究中,基本理论和传播模型是两个主要方向[2]. 基本理论主要关注信息传播规律、影响因素和机制[3],如网络结构、节点属性、信息内容等对信息传播过程的影响[4]. 网络结构分析主要关注社交网络中信息传播的特点,如小世界现象和幂律分布等[5];节点属性研究则关注个体在信息传播中的角色,包括意见领袖、桥接节点等;信息内容研究主要关注信息本身的特性,如话题、情感和传播力等,以及这些特性如何影响信息在社交网络中的传播[6].
传播模型则主要用于描述和预测信息传播过程[7]. 国内外的学者提出了很多模型,而其中最著名的是独立级联模型(ICM)[8]和线性阈值模型(LTM)[9]. 在独立级联模型中每个节点有一定的概率被其邻居影响,从而采纳某种行为或观点. 这个概率通常根据节点间的关系强度来确定[10]. 线性阈值模型则认为节点在邻居中所占的影响力达到一定阈值时,才会采纳新的行为或观点[11]. 此外,还有其他的传播模型,例如信息扩散模型(IDM),为国内外学者提供了多种信息传播过程的建模方法[12]. 尽管学者们在社交网络信息传播研究中取得了显著成果,但这一领域的研究仍然面临诸多挑战. 社交网络中信息传播往往受多方面因素的影响,如时效性、跨平台传播和社交媒体上的算法推荐等. 这些因素使信息传播的规律和模式变得更加复杂,给信息传播研究和预测带来了困难.
由于重叠节点在社交网络中起到关键作用,尤其在信息传播过程中具有特殊意义[13],在过去的研究中尽管学者们提出了许多方法来挖掘这些重叠节点(包括基于社区划分的方法[14]、基于网络结构的方法[15]、基于随机游走的方法[16]及基于机器学习的方法)[17],但是由于节点的动态性、社区结构的复杂性及信息传播的多样性,仍然对社交网络中挖掘重叠节点造成了困难和挑战. 在动态社交网络中,节点和边的变化频繁,传统的社区检测方法往往难以应对这种变化[18]. 此外,社交网络中的社区结构通常具有重叠性,即一个节点可能属于多个社区,这种状态给社区检测带来了额外的复杂性[19].
为了解决目前研究的不足,本文提出一种面向社交网络重要信息传播的重叠节点挖掘模型(SNONMM),该模型综合了标签传播算法(LPA)和扩散激活原理,旨在克服现有方法的局限性. 标签传播算法通过在网络中传播节点标签来发现社区结构;而扩散激活原理则模拟了信息在网络中的传播过程. 两者相结合使SONMM模型能够有效地挖掘社交网络中的重叠节点.
全文HTML
-
动态网络通常由一个网络G(V,E)表示,其中V是顶点的集合,而E是边的集合. 本文定义动态网络SG为一组顺序网络SG={G1,G2,…,Gt},其中每个网络对应一次迭代. 例如,G1对应第一次迭代,t表示从1开始的迭代编号. 由于本文方法和其他可用方法都是为动态重叠社区检测提供的,因此本文模型考虑了这类社区. 重叠动态社区检测是指在SG中找到密集连接的重叠子网络任务.
扩散激活过程是一种搜索方法,通过在网络中随机选择一个或多个节点作为源节点开始. 每个节点都对应一个初始化激活值,源节点的激活值为1,其他节点的激活值为0. 每个节点的激活值表示该节点传播信息所需的激活量. 每个源节点通过广度优先搜索方法将其激活值发送给其他节点. 如式(1)所示,接收节点根据以下3个参数更新它们的激活值:①源节点的激活值;②源节点与目标节点之间的链接权重;③衰减因子.
衰减因子是表示网络边缘扩散强度减小的参数. 当从多条路径到达一个节点时,该过程停止. 每个源节点创建一个由其可访问节点组成的树. 总的来讲,节点j的激活值是基于节点i的激活值计算获得,其中i是源节点,j是目标节点. A[i]和A[j]分别是节点i和j的激活值. D是衰减因子,W[i,j]表示节点i和j之间的链接权重.
-
SNONMM主要由4个部分组成. 第1部分是初始化,其中每个节点都被标记为一对标签名称,激活值. 本文首先将标签名称设为节点编号,激活值设置为1. 标签名称用于区分节点,而激活值表示节点的状态或活跃程度. 第2部分是网络权重分配,应用了名为社交行为信息扩散模型(SBIDM)的权重算法. 这种算法为每个节点分配一个分数,并从得分最高的邻居即最佳邻居处获取基于信息. SBIDM算法的基本原理是通过节点社交行为来分配权重,从而使信息传播更加高效. 在确定最佳邻居后,通过增加节点与其最佳邻居之间的边来提升该节点的状态值:
式(2)中:
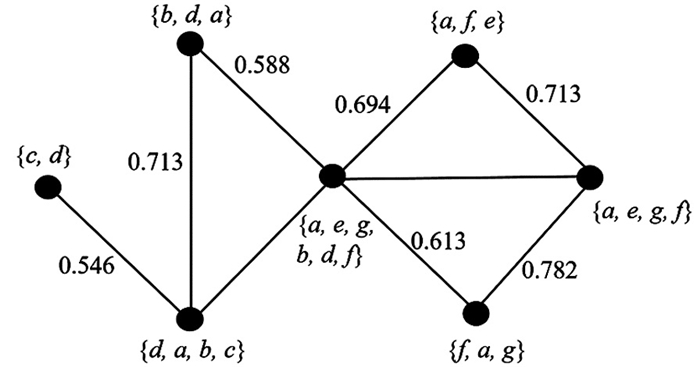
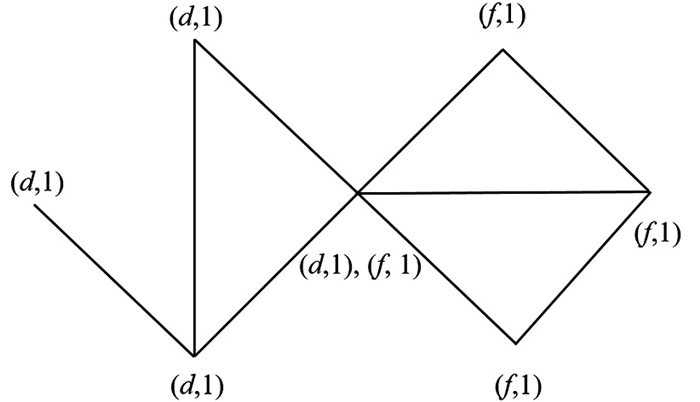
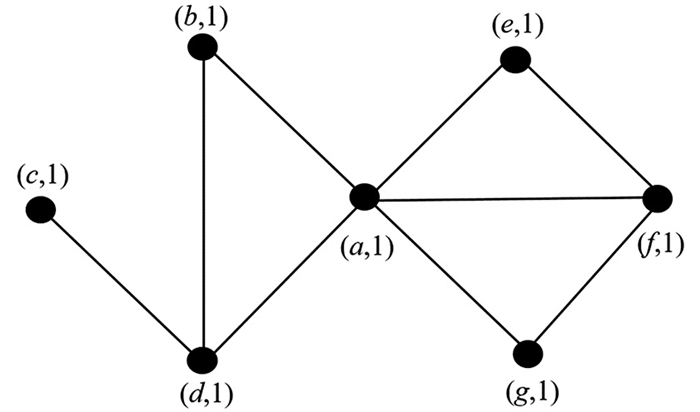
这种权重算法旨在实现目标边的权重越大,则信息流量越大. 本文在具有7个顶点的网络中进行了应用,其中图 1和图 2显示了SNONMM在具有7个顶点的网络中第1部分和第2部分的结果.
第3部分为所有节点考虑预定义权重的自循环(图 3),应用了扩散激活过程,其中所有新节点而非少数节点被选择为源节点. 每个源节点首先将其标签激活值发送给自身,然后将其发送给通过广度优先搜索访问的其他节点,直到达到目标状态(激活值低于阈值). 每个目标节点根据3个参数更新接收标签的激活值. 第1个参数是源节点的激活值,第2个参数是源节点和目标节点之间的边的权重,第3个参数是衰减因子. 当过程完成时,激活值较低的标签将从节点中移除.
第4部分首先将更改的节点按随机顺序排列,然后从该顺序中选择一个节点作为接收节点,提取其邻居并将其视为发送节点,每个发送节点选择激活值大于其他标签的一个标签. 发送节点将其选定的标签发送给接收节点,接收节点根据发送节点和接收节点之间的边的权重计算发送标签的新激活值. 接收节点对相同标签的激活值求和,然后接受激活值之和大于其他标签的标签. 如果接收标签的激活值大于1,算法将其设置为1,作为激活值范围的结果. 第4部分重复进行5~20次,删除激活值较低的标签. 具有近似激活值标签的节点形成社区. 图 4显示了SNONMM在网络中第4部分的结果,表明节点(a,e,f,g)和(a,b,c,d)在同一个社区中.
-
算法首先为所有新节点分配最大激活值,然后开始边权重处理过程. 算法1首先将所有边的权重初始化为1,然后随机选择一个节点并计算其邻居的分数. 在邻居中,分数大于其他节点的节点被选为最佳邻居. 本文将节点与其最佳邻居之间的权重加上该节点的状态值. 函数Normalize(G(V,E))调整边的权重,使每条边的权重不超过1.
算法1 SBIDMEdgeWeighting(Gts)
Input:G=(V,E)
Output:WG:weighted graph
Method:
1.for each e_m in E
2.set w(e_m)=1
3.end for each
4.for i:=1 to n do
5.Choose node v randomly
6.Calculate score for neighbors of v
7.best_neighbor=select_best_neighbor(neighbor_scores)
8.if best_neighbor exists then
9.Update edge weight between v and best_neighbor based on Eq. (3)
10.Update activation values of v and best_neighbor based on Eq. (2)
11.end if
12.end for
13.for each node v in V do
14.for each neighbor u of v do
15. Normalize edge weight between v and u
16.end for each
17.end for
18.WG=G(V,E)
算法2中函数Spreading Activation(G(t))计算节点的激活值. 首先为每个节点创建一个名为UnFiredNodeSet的空集,然后根据广度优先搜索进行更新. 从这个集合中提取节点,并计算它们的激活值,直到激活值低于阈值或者UnFiredNodeSet为空.
算法2 Spreading Activation (G(t),new nodes)
Input:G(V,E)
Output:G(V+,E)
Method:
1.for each node v in V do
2.Create empty set UnfiredNodeSet
3.Add v to UnFiredNodeSet
4.Neighbors=v.ObtainNbs()
5.Add Neighbors to UnFiredNodeSet
6.while UnFiredNodeSet is not empty do
7.Extract nv from UnFiredNodeSet
8.Compute nv.label.activation_value
9.If nv.label.activation_value<threshold
10.continue
11.end if
12.Neighbors=nv.ObtainNbs()
13.Add Neighbors to UnFiredNodeSet
14.end while
15.end for
算法3开始标签传播. 首先通过ShuffleOrder函数将更改的节点按随机顺序排列,并从这个顺序中选择一个节点作为接收节点,通过函数ObtainNbsO提取接收节点的邻居作为发送节点. GetLabelsO函数选择每个发送节点中激活值最大的一个标签,创建发送标签的候选标签集. 然后,接收节点接受候选标签集中激活值之和最大的一个标签. 最后,删除激活值较低的标签,并根据标签激活值的相似性提取社区.
算法3 SNONMM算法
Input:SG={L_1=〈V_1,E_1〉,L_2=〈V_2,E_2〉,…,L_n=〈V_n,E_n〉},T
Output:set of communities of SG
Method:
1.Initialize communities
2.for ts=1:T do // ts stands for timestamp
3.for each node v in SG do
4.Node(v).label=v
5.Node(v).label.activation_value=1
6.end for
7.Initialize G(ts)
8.end for
9.Initialize deltaV
10. ΔV={v|v ∈V(ts)}.3
11.for ts=1:T do
// Part 2:Edge Weighting
12.WERW-KpathEdgeWeighting (G(ts)) or SBIDMEdgeWeighting (G(ts))
// end Part 2
// Part 3:Spreading Activation
13.Spreading Activation (G(ts))
// end Part 3
// Part 4:label propagation
14.ChangedNodes={u,v|(u,v)∈E(ts)}
15.V_old={v|v∈G(ts)∩v∉G(ts+1)}
16.ChangedNodes=ChangedNodes-V_old
17.for it=1:IT do // it means iteration
18.ChangedNodes.ShuffleOrder()
19.for i=1:ChangedNodes.count do
20.Receiver=ChangedNodes(i)
21.Senders=ChangedNodes(i).ObtainNbs()
22.CandidateLabels=Senders.GetLabels()
23.Receiver.update(CandidateLabels.TheMostActivationValueLabel)
24.end for
25.end for
26.Remove Nodes(i) labels with activation value<r
27.Update communities
28.Update SG
// end Part 4
29.end for
-
本文方法分为4个部分. 第1部分中初始化标签需要O(n),其中n是节点数量. 第2部分中应用了权重算法. 在最坏的情况下这一部分需要O(m),其中m是边的数量. 第3部分中由于本文方法对网络每个节点使用广度优先搜索,因此总共需要O(n×m). 第4部分包括发送和接收标签,需要O(n). 从上述事实可以得出,本文方法在每次迭代中需要O(n×m). 由于迭代次数是一个常数T,所以所有社区检测的总复杂度为O(n×m).
1.1. 动态网络和扩散激活过程
1.2. SNONMM原理描述
1.3. 模型的算法实现
1.4. 复杂度分析
-
本文选择2个引文网络和1个合成网络对SNONMM进行评估. 在引文网络中只能添加节点,因此与前一次迭代相比节点数量有所增加. 在本文中,有向边被视为无向边.
-
Arxiv HEP-PH是一个引文网络,涵盖了1993年1月至2003年4月期间发表的论文,包含34,546个节点和421,578条边,其中节点是论文,边是论文之间的引用. 因此,从节点i到节点j的边被视为论文i和j之间的引用. 该数据集将1个月的论文和交流视为1次迭代.
Arxiv HEP-TH是一个覆盖高能物理理论出版物的引文网络,论文被视为节点,论文之间的引用被视为边,该网络包含27,770个节点和352,807条边. 数据集涵盖了1993年1月至2003年4月期间的论文,且将两个月的论文和交流视为1次迭代. 引文数据集的基本信息如表 1所示.
除2个真实引文网络外,本文还将SNONMM与其他可用方法的性能在一个人工合成网络中进行评估,生成这些网络的核心参数如表 2所示. 其中,S表示迭代次数,n表示节点数量,avgd和maxd分别表示节点的平均度和最大度,符号minc和maxc分别表示社区的最大和最小规模,符号On和Onc分别表示重叠节点的数量和每个重叠节点所属的社区数量,μ是设定为0.3的混合参数.
-
本文中由于真实网络缺乏已知的基准社区,因此采用模块度衡量和标准互信息方法来评估检测模型的准确性.
-
尽管原始模块度主要处理非重叠社区,但在本文中社区成员可以相互重叠. 因此,如式(4)所示,本文采用了一种拓展模块度方法,以便衡量具有重叠结构的社区.
式(4)中:
式(4)、式(5)中,符号ki和kj分别表示顶点i和j的度. 符号m表示边的数量,Ai,j是邻接矩阵. 符号βiC和βjC分别表示节点i和j属于社区c的强度. 符号kiC和kjC分别表示节点i和j到社区c的链接总权重.
-
由于在人工合成网络中已知社区结构,因此使用标准互信息(Normalized Mutual Information,NMI)[20]作为评估社区检测的指标. NMI值的范围在0~1之间,当算法划分的社区结构更准确时,NMI值较大;若不太准确,则NMI值较小.
-
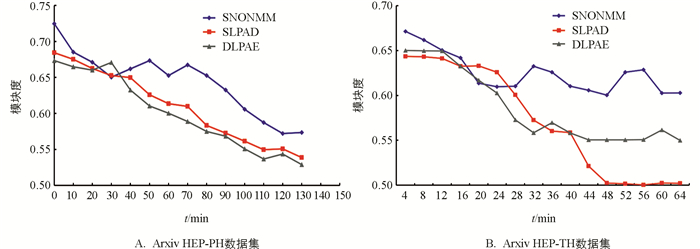
本文选择了动态的Speaker-Listener标签传播算法(SLPAD)[21]和基于动态网络标签传播的进化聚类算法(DLPAE)[22]来与SNONMM在真实网络和人工合成网络中的结果进行对比,分别显示在图 5和图 6中. 选择SLPAD和DLPAE方法是因为它们都能在动态社交网络中检测到重叠社区.
图 5A绘制了Arxiv HEP-PH数据集上本文方法与其他可用方法在模块度方面的比较结果. 从图 5A的数据中可以明显看出所有方法(包括本文的SNONMM和其他可用方法)呈现出递减趋势. 这是因为所有方法在第1次迭代中考虑了整个网络,而在迭代2及以后的迭代中与前一次迭代相比,考虑了发生变化的边和节点. 由于迭代2及以后的迭代中考虑了变化的边和节点,因此模块度的减少不可避免. 此外,SNONMM在早期迭代中的模块度减少量大于SLPAD和DLPAE. 然而,在中间和最后的迭代中,本文方法模块度的减少量小于其他可用方法. 从以上事实可以得出,SNONMM在节点和边变化方面的性能优于其他可用方法. 图 5B绘制了Arxiv HEP-TH数据集上SNONMM方法与SLPAD[20]和DLPAE[21]方法在模块度方面的比较. Arxiv HEP-TH数据集中迭代数量是Arxiv HEP-PH数据集的一半,而数据集中的节点数量大致相同,由于在此数据集中节点仅被添加而没有被删除,新节点的数量远低于Arxiv HEP-PH数据集. 在早期迭代中SLPAD和DLPAE方法表现出增长趋势,而在后期迭代中它们的准确性显著降低. 除了早期迭代外,SNONMM在大部分迭代中都实现了更高的模块度. 图 6显示了3种方法在人工合成网络中得出的结果,可以看出SNONMM在人工合成网络中的NMI值同样大于SLPAD[20]和DLPAE[21]方法,即SNONMM在社区划分时得到的结果相较于其他两种方法具有更高的准确度.
基于上述结果,SNONMM方法在上述3个数据集中取得了比其他两种方法更好的性能.
2.1. 数据集介绍
2.2. 评价指标
2.2.1. 模块度衡量
2.2.2. 标准互信息(NMI)
2.3. 实验结果
-
本文针对社交网络中重要信息传播的重叠节点挖掘问题进行了深入研究,并提出一种面向社交网络重要信息传播的重叠节点挖掘模型(SNONMM). 该模型结合标签传播算法(LPA)和扩散激活原理,能够在动态社交网络中提高社区检测的准确性,使新节点在社交网络中向其他节点传播标签的机会大于旧节点,且每个标签都有一个表示其传播强度的激活值. 通过对2个真实网络和1个人工合成网络的实验评估,本文发现SNONMM方法在检测社区准确性方面优于其他可用方法,表明SNONMM在解决动态社交网络中重叠节点挖掘问题方面具有潜在优势. 然而,动态网络中的社区检测仍然具有挑战性,尤其是在动态社区发现方面,尽管本文SNONMM在一定程度上解决了这个问题,但未来的研究仍需进一步探讨和优化这些方法,以提高其在更广泛应用场景中的性能. 在未来的研究中,可以考虑对网络结构和社交媒体上的内容进行融合,以提高社区检测的准确性和效率,并结合多层次和多维度数据,更好地捕捉和描述动态社交网络中的社区结构变化,同时可以开发更多针对动态网络的社区检测算法,并对它们进行跨学科综合研究,以提高算法的通用性和适应性.



 下载:
下载: