-
开放科学(资源服务)标识码(OSID):

-
随着科技的发展,人体动作捕捉技术在现代生活各个领域中的应用越来越广泛[1-2].通过深入研究人体动作捕捉技术,可以提高其在各领域的应用效果,为人们的生活带来更多便利.例如,在电影制作中更加精准的动作捕捉技术可以带来更真实的动画效果,提升观众的观影体验;在体育训练中运动员可以利用动作捕捉技术更好地纠正姿势,提高竞技水平;在医疗领域精确的动作捕捉技术可以帮助医生更准确地评估病人的运动功能,制定个性化康复方案,促进患者康复.因此,对人体动作捕捉技术的研究具有重要的现实意义和实用价值.然而,人体动作捕捉技术在提取动作时存在一些难点[3].首先,由于人体运动的复杂性和动态性,如何准确、快速地采集和处理运动数据是研究的难点之一.由于人体姿势和运动状态的多样性,如何对数据进行标准化处理和特征提取也是需要解决的技术难题.对人体姿态进行准确估计和对行为进行识别是人体动作捕捉技术的核心难点.由于人体姿态和行为的复杂性,如何利用算法和模型对其进行准确判断和识别是一项具有挑战性的任务.同时,如何克服遮挡、动态背景等干扰因素也是研究的重点之一.在传统的人体动作捕捉技术中,Kinect深度相机在获取人体骨骼点信息时存在一定的误差和不稳定性,容易受到环境光照、人体姿态等因素的影响[4-5].其次,不同的人完成相同动作的速度可能存在差异,因此需要一种能够适应不同动作速度的算法来提取人体动作[6].针对这些问题,本文提出Levenberg-Marquardt算法,简称为LM算法,并采用粒子群算法对其加以优化.同时,引入动态时间规整算法(Dynamic Time Warping,DTW),以期提高人体动作捕捉的精度和稳定性.本文的创新性在于将LM算法与DTW算法相结合,构建了一种新型的人体动作捕捉方法.其中,改进的LM算法能够准确地获取骨骼点信息,DTW算法能够自动调整时间尺度,以适应不同长度的动作姿态,使不同速度下的人体动作能够进行准确匹配和比较,为人体动作捕捉领域提供了更加可靠的数据支持.该方法为“设计+”国家级众创空间建设项目的实施提供了有效的技术支持.
全文HTML
-
在进行人体动作捕捉时,获取人体骨骼点的位置信息至关重要.本文主要采用Structured Light深度相机进行人体骨骼电信息的获取,这是一种基于光学原理的深度感应技术,能够通过投射已知结构的光线,并分析反射回来的光线来获取深度信息.这种深度相机具有高精度和高分辨率的特点,能够准确地测量人体表面的深度信息,从而获取人体骨骼点的位置信息[7-8].
由于Structured Light深度相机在采集人体骨骼点数据时可能会出现抖动或自遮挡等问题,因此本文提出一种改进的骨骼点坐标拟合优化算法,即LM算法.该算法结合了梯度下降法和Gauss-Newton法,是一种利用标准数值优化计算的快速算法[9].在LM算法中阻尼系数作为一个关键参数,控制着算法的行为.当阻尼系数逐渐增大时,LM算法的特性逐渐接近于梯度下降法,沿着梯度下降的方向寻找最优解,利用其全局优化的特性[10],如式(1)所示.
式(1)中,xn表示第n步的解,α为学习率,▽f(xn)表示函数f(xn)在xn处的梯度.当阻尼系数逐渐减小时,该算法的特性与Gauss-Newton法相似.算法在迭代过程中更注重局部收敛,通过拟合欧拉角能量值E获取骨骼点之间最合适的距离长度[11],如式(2)所示.
式(2)中,f(x)表示目标函数,g(x)表示约束条件,d是搜索方向.f(x)的计算如式(3)所示.
式(3)中,y表示观测值.约束条件如式(4)所示.
式(4)中,θ表示欧拉角.EIK(θ,d)、ES(θ,d)、Ed(θ,d)分别代表逆运动学约束项、平滑约束项和深度约束项,ωIK、ωS、ωd分别表示各项的约束系数.在人体动作捕捉中,该算法首先将Kinect算法生成的三维骨骼点坐标作为待优化的主要参数.利用OpenPose算法进行图像映射及对齐操作后获得的三维骨骼点坐标,被用作后续拟合的关键参数.本文选定人体骨架的胯中心点作为根节点,并将其坐标也纳入拟合参数中.在优化过程中,LM算法的核心是将各个骨骼点之间的欧拉角视为主要优化变量,为确保优化结果的稳定性,新获取的骨骼方向和长度均与原始骨架保持一致[12].由于传统的LM算法过度依赖初始值,因此本文引入粒子群算法(Particle Swarm Optimization,PSO)生成LM-PSO算法.LM-PSO算法结合了LM算法和PSO算法的优势.LM算法在接近局部极小值时有快速收敛和高精度搜索的特点,使算法在局部范围内能够快速找到最优解.PSO算法则具有全局范围内的快速搜索和收敛能力,能够在更大的解空间中寻找最优解.通过融合这两种算法,LM-PSO算法不仅继承了LM算法的局部搜索优势,还利用了PSO算法的全局搜索能力.该算法既能够在局部范围内快速找到最优解,又能够避免过度依赖初始值的问题,同时还能避免PSO算法容易陷入局部极值的缺陷[13-14].
PSO算法是一种基于群体智能的优化算法.该算法模仿鸟群、鱼群等生物群体的社会行为,通过个体与群体之间的信息共享和个体之间的相互协作,寻找问题的最优解.在PSO算法中,每个解都被看作是搜索空间中的一个粒子,而每个粒子都有一个速度和位置.在算法的初始化阶段随机生成一组粒子,每个粒子代表一个可能的解,然后通过迭代方式根据每个粒子自身的历史最优位置和群体的历史最优位置来更新自己的速度和位置.LM-PSO算法首先使用PSO算法对目标优化函数进行求解,获得一个优化控制量,即群体最优解.在PSO算法中每个解都被看作是搜索空间的一个粒子,而每个粒子都有一个速度v和位置p.在算法的初始化阶段随机生成一组粒子,且每个粒子代表一个可能的解,通过迭代方式根据每个粒子自身的历史最优位置pi和群体的历史最优位置pgbest来更新自己的速度和位置.粒子的速度更新如式(5)所示.
式(5)中,w表示惯性权重,c表示加速常数,r为随机数,p代表粒子的当前位置.粒子位置更新如式(6)所示.
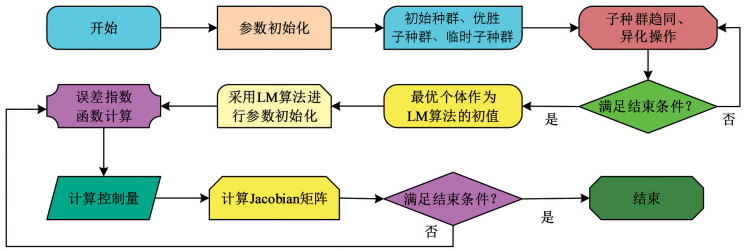
通过迭代更新粒子的速度和位置,PSO算法可以找到目标优化函数的最优解.在LM-PSO算法中,最优解被用作LM算法的初始值,且通过LM算法进一步优化求解.然后,再将该结果作为LM算法的初始值,经过多次迭代计算求得符合条件的最优解,该解即为最优控制量.LM-PSO算法的基本流程如图 1所示.
本文以右手各个骨骼点的骨骼链为例,详细介绍基于LM-PSO的拟合优化算法.该算法旨在实现对手部骨骼点数据的优化处理,从而提高手部动作识别的准确性和稳定性.假设已知右肩骨骼点的坐标Prs,右手肘骨骼点的坐标Pre以及左手骨骼点的坐标Prh.从右手肘骨骼点到右肩骨骼点的方向向量为
$\overrightarrow{T_{rers}}$ .同理,从右手肘骨骼点到右手骨骼点的方向向量为$\overrightarrow{T_{rerh}}$ .然后,通过计算拟合优化后右肩骨骼点到右手肘骨骼点及右手肘骨骼点到右手骨骼点的长度,即可获取拟合优化后右手肘及右手骨骼点的坐标.LM-PSO算法主要是通过拟合骨骼点之间的欧拉角θ来获取骨骼点之间最合适的距离长度.这个过程是通过迭代进行的,随着迭代训练中未知骨骼点数量增加,拟合效果会逐渐改善,但同时也会增加计算量,导致处理速度略有下降. -
获取到拟合优化后的骨骼点坐标后,接着进行人体动作检测[15].针对采集的动作序列与标准动作序列在时序上的差异问题,本文引入了DTW算法.该算法通过动态规整两个时间序列的形状,将它们按最优路径对齐,并计算它们之间的相似度,进而实现人体动作的精准捕捉.其主要通过逐步拉伸或压缩时间序列中的元素来找到最佳匹配,计算累计距离,并最终得到一个累积距离矩阵.该矩阵中的最小值表示两个时间序列之间的相似度.DTW算法充分考虑了时间序列中元素之间的时序关系,适用于比较不同长度和变化速度的时间序列,同时具有较好的鲁棒性,对于时间序列中的噪声、数据缺失等问题有一定的容忍度.此外,该算法还可以处理时间轴上的偏移、缩放和扭曲等变形,使不同个体的动作数据能够更好地对齐和比较[16-17].该算法的主要思想是通过动态规划方式,逐步构建一个最优路径,使两个序列之间的累积距离最小.假设有一个测试序列G,其长度为t;一个标准序列H,其长度为m.测试序列如式(7)所示.
标准序列如式(8)所示.
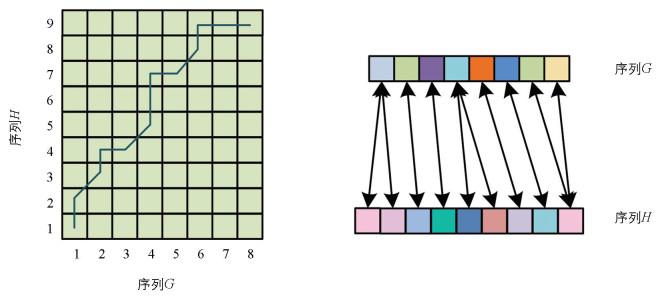
其中,gi和hi在维度上相同,t和m可以不同[16-17].u(g1,h1)表示g1与h1的距离值,简化为u(1,1),采用欧氏距离方法计算.U(G,H)为某条路径的总距离,即由g1和h1的距离值u(g1,h1)经过若干个节点对,到gt和hm距离值u(gt,hm)的累计距离和,如式(9)所示.
为了确保在G和H中找到全局最优路径,需要满足3个条件:①边界条件需要满足路径从起点(1,1)开始,到终点(t,m)终止;②所选路径必须确保在时间顺序上单调递增;③在匹配过程中,不能跳过某个点去匹配.此外,为了防止路径斜率过大或过小,通常将斜率限制在0.5~2的范围内,以得到全局最优路径[18].整合以上条件,DTW算法如式(10)所示.
序列G和序列H的匹配路径和对应关系如图 2所示.
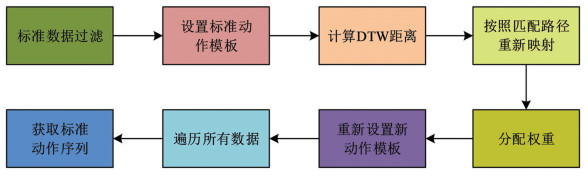
在现代各个领域的动作设计中,动作标准化非常重要[19].本文主要采用DTW算法,通过比较实验人员的动作序列与标准动作序列的相似度来判断实验人员的动作是否标准,因此需要先设计标准动作库[20].通过将多个人的标准动作数据流进行整合,从而得到标准动作库.为了得到更准确的标准动作序列,本文邀请了10名动作测试员进行标准动作采集.在采集过程中所有测试人员需经过多次练习以确保动作标准化,随后进行数据采集.每个动作重复5次,共获得50组动作数据.考虑到采集的数据可能存在噪声,因此需要采用可调整窗宽的滑动窗口滤波器对数据进行过滤,然后选取第一组数据作为初始的标准动作模板.接着,计算下一个序列与第一组模板之间的DTW距离,并与预设的阈值进行比较.如果距离超出了阈值,将剔除该组数据;如果距离在阈值范围内,则将两个动作序列按照DTW算法的匹配路径进行重新映射,并对两个序列分配不同的权重.其中,模板序列的权重为0.8;下一个序列的权重为0.2.最后,计算对应序列的加权值作为新的标准动作模板.重复上述迭代过程,直至遍历完所有数据,以获取更准确、更具代表性的标准动作序列.具体操作流程如图 3所示.
在动作捕捉过程中,由于个体动作的速度差异及个体与标准动作之间的非帧频对应关系,即使动作尽量保持标准,动作序列与标准动作序列在时间轴上也可能存在一定误差[21].针对这一问题,本文采用DTW算法实现动作序列与标准动作序列对齐,从而提高动作识别的准确率.在对齐过程中如果两个序列的差距越大,则说明所评估的动作与标准动作的差异越大,即动作越不标准.为了减少个体差异对动作识别的影响,本文将骨骼点坐标的时间序列转换为骨骼点角度的时间序列,再与标准序列进行比较.这种转换可以消除不同个体在空间坐标上的差异,从而更好地反映动作的特征.
以“左肩外展曲肘”这个简单动作为例,该动作表示左手从自然下垂状态抬起到180°的水平状态,然后保持大臂稳定不动,弯曲左手肘,让左胳膊的小臂和大臂呈直角形状,最后恢复手臂自然下垂状态.在这个动作中将左肩和左手肘两个骨骼点角度的时间序列,作为标准动作估计的动作序列.假设左手腕、左手肘、左肩及左胸脊点的三维空间坐标点分别为Plw,Ple,Pls,Plb,左手肘骨骼点及左肩骨骼点的角度分别为Ale,Als.则左手肘骨骼点角度Ale如式(11)所示.
左肩骨骼点角度Als如式(12)所示.
采用DTW算法,分别计算实验者左肩骨骼点时间序列与标准动作左肩骨骼点时间序列之间的DTW距离Drs和路径长度Krs.同样地,也计算实验人员左手肘骨骼点时间序列与标准动作左手肘骨骼点时间序列之间的DTW距离Dre和路径长度Kre.“左肩外展曲肘”的相似度计算如式(13)所示.
式(13)中,Wrs,Wre分别表示左肩和左手肘骨骼点在动作评估中的权重.此外,需要设定一个阈值ω,若DTWvalue小于(等于)该阈值,则代表动作标准,反之则不标准.基于LM-PSO-DTW算法的人体动作捕捉的具体实现步骤为:①采用Structured Light深度相机获取人体的二维RGB图像和三维深度图像;②采用LM-PSO算法对映射得到的三维骨骼点坐标进行拟合优化;③采用DTW算法进行人体动作捕捉及评估.
1.1. 基于改进LM算法的人体动作捕捉
1.2. 基于DTW算法的人体动作评估
-
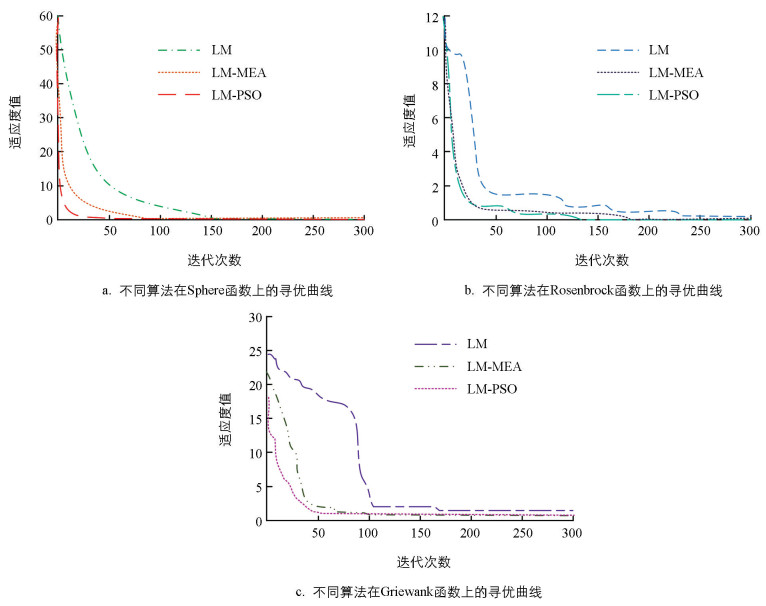
本文进行了一系列实验验证LM-PSO-DTW算法的有效性,所有实验测试均在相同的实验环境下进行.实验电脑系统为Windows 10操作系统,内存为16 GB,处理器为Intel i7-7700处理器,显卡为NVIDIA GTX 1060 6G.图像采集采用PrimeSense公司研发的Structured Light深度相机.首先验证改进LM-PSO算法的优越性,选取传统的LM算法、思维进化算法与LM算法的结合算法(Mental Evolutionary Algorithm,MEA)与之进行性能对比,并采用3种不同结构的经典Benchmark函数对各个算法进行仿真测试.其中,Sphere函数是一种单峰球面函数,易于求解,常被用于检验算法精度和观察其执行能力.Rosenbrock函数是一个非凸、病态函数,也被称为Banana函数,其全局最优解与局部最优解在一个类似狭长山谷的区域内.Griewank函数是一种常用于测试优化算法性能的多峰函数,有多个局部最小值,使得找到全局最小值变得更加困难.各个算法在不同函数上的寻优曲线如图 4所示.由图 4可知,在各个函数寻优曲线上,本文提出的LM-PSO算法寻优速度更快,且均能在最少迭代次数内获取全局最优解,其次是LM-MEA算法.其中,在Sphere函数中LM-PSO算法仅迭代至30次时即获取到全局最优解,而LM-MEA算法在80次左右获取全局最优解,LM算法则在150次左右获取全局最优解.在Rosenbrock函数中,LM-PSO算法仅迭代至130次时即获取到全局最优解,相较于LM-MEA算法减少了45次.而LM算法在初始求解时容易陷入局部最优解,且迭代至230次左右趋于稳定,但可能无法获取到全局最优解,表明其对初始值的选择非常敏感,而LM-PSO算法和LM-MEA算法均有效改善了陷入局部最优的情况.在Griewank函数中,LM-PSO算法仅迭代至50次即获取到全局最优解,说明本文所提算法具有显著的性能优势.
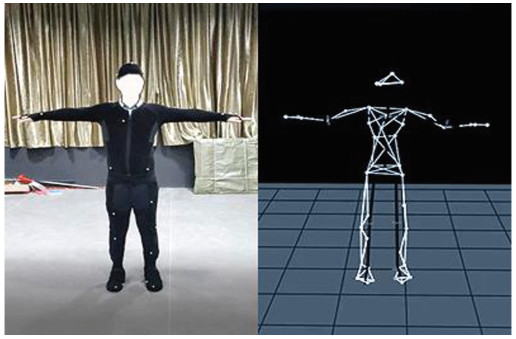
本文进一步验证了LM-PSO-DTW算法动作捕捉的准确度,选取肩部推举、阿诺推举、肩部侧平举、深蹲4个动作进行研究.这些动作可以涵盖身体的各个部位,并能够有效地提取实验所需的骨骼点信息.当人在健身时获取的人体骨骼点信息如图 5所示.
实验选取目前较为先进的基于自适应移位图卷积神经网络(Adaptive Shift Graph Convolutional Neural network,AS-GCN)的人体动作捕捉算法、基于时空注意力机制与时空图卷积网络(Spatial-Temporal Attention Mechanism and Spatial-Temporal Graph Convolutional Network,SAT-GTCN)的人体动作捕捉算法进行实验对比分析.为了测试动作识别的准确性,实验邀请了50位志愿者进行这些动作的重复性测试,所有志愿者年龄为18~60岁,身体健康,无任何影响完成动作的障碍.本研究设置了一个专门的实验室用于数据采集,室内光线稳定,无明显的光源变化.使用的设备包括高分辨率摄像机、动作捕捉系统及相关软件.每名志愿者需完成肩部推举、阿诺推举、肩部侧平举、深蹲4个动作,每个动作10次,共得到500组数据.测试时,志愿者与相机的距离统一设置为3 m,测试角度为0°.在志愿者进行动作的同时,使用高分辨率摄像机和动作捕捉系统记录他们的动作.完成数据采集后对所有的动作帧进行预处理,包括去噪、人体关键点检测和标注等,然后使用特定算法对标注的关键点进行动作识别,最后取所有测试数据的平均值作为最终结果.实验还对比了不同算法在动作捕捉全程的测试时间.不同算法在测试中的识别率及测试时间对比结果如图 6所示.由图 6a可知,本文提出的LM-PSO-DTW算法对各个动作的捕捉准确率最高,其中对肩部侧平举这一动作的捕捉准确率最高达到了96.58%,相较于AS-GCN算法与SAT-GTCN算法分别提升了2.14%,0.71%.其对肩部推举、阿诺推举及深蹲这3个动作的识别准确率分别高达97.81%,98.01%,99.35%,相较于AS-GCN算法分别提升了3.28%,6.67%,6.49%.由图 6b可知,LM-PSO-DTW算法对各个动作的测试时间较短,其中对深蹲动作的测试时间最短,仅为1.15 s,相比于AS-GCN、SAT-GTCN算法分别减少了0.41 s,0.24 s.虽然LM-PSO-DTW算法对阿诺推举这一动作的测试时间相对较长,高于AS-GCN、SAT-GTCN算法,但其总体性能明显优于AS-GCN、SAT-GTCN算法,表明LM-PSO-DTW算法在进行动作捕捉时,明显优于其余算法,具有更强的可行性.
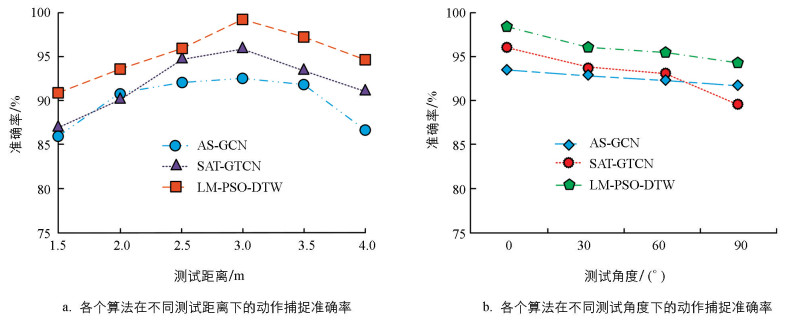
为了验证LM-PSO-DTW算法的可靠性,本文继续从不同测试距离、不同角度测试各个算法的动作捕捉准确率.其中,志愿者与深度相机的距离分别设置为1.5 m,2 m,2.5 m,3 m,3.5 m及4 m.测试的角度分别为0°,30°,60°,90°.当进行不同距离的测试时,保持测试角度为0°;当进行不同角度的测试时,保持测试距离为3 m.选取肩部推举作为测试动作,每组测试需要收集50名志愿者的100个数据,并取平均值作为最终测试结果.各个算法在不同测试距离及测试角度中的动作捕捉准确率如图 7所示.由图 7a可知,各个算法的动作捕捉准确率随着测试距离增加呈现出先增后减的趋势,其中测试距离为3时算法的准确率最高.LM-PSO-DTW算法在不同测试距离下均优于其余两种算法.具体来讲,LM-PSO-DTW算法在测试距离为3 m时的动作捕捉准确率高达99.35%,相较于AS-GCN,SAT-GTCN算法分别增加了7.24%,4.01%.由图 7b可知,各个算法的动作捕捉准确率随着测试角度增大呈现出下降趋势,当相机正对志愿者时,各个算法的准确率最高.LM-PSO-DTW算法在不同测试角度下的动作捕捉准确率均优于其余两种算法.其中,LM-PSO-DTW算法在测试角度为30°时的动作捕捉准确率高达96.87%,相较于AS-GCN,SAT-GTCN算法分别增加了3.57%,2.68%,表明LM-PSO-DTW算法在进行动作捕捉时具有更可靠的性能优势.
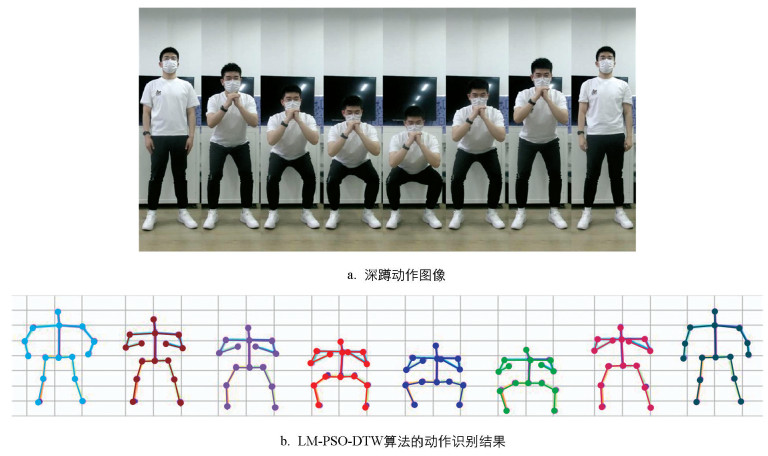
图 8展示了LM-PSO-DTW算法对深蹲动作的实际检测效果.从图 8中可以看出,在背景较为复杂的情况下,LM-PSO-DTW算法仍然能够精准捕捉到人体的骨骼点信息,并进行有效的人体跟踪,具有较高的鲁棒性及准确性.
为验证LM-PSO-DTW算法的有效性,本文继续进行消融实验.采用的数据集为Human 3.6M,该数据集是目前3D领域中样本数量最多、使用最为广泛的数据集.包含了约360万个3D人体姿势和相应的图像,共有11个实验者和17个动作场景.LM-PSO-DTW算法的消融实验结果如表 1所示.由表 1可知,仅采用DTW算法的识别准确率为74.25%.当加入LM模块时,算法的识别准确率提升至89.02%,原因在于LM模块能够学习数据的内在模式,从而更好地指导算法进行姿态估计和识别.当加入PSO算法时,算法的识别准确率提升至92.15%,原因在于PSO算法能够找到最优解或近似最优解,进一步提高了姿态估计和识别的准确性.本文所提出的LM-PSO-DTW算法识别准确率高达98.39%,明显优于其余算法,再次验证了其有效性及鲁棒性.
-
针对现有动作捕捉技术存在捕捉不准确、计算效率低等问题,本文引入改进的LM-PSO算法,同时针对动作捕捉与评估引入DTW算法,提升人体动作捕捉的准确性.结果表明,本文提出的LM-PSO算法在各个函数上表现出更快的寻优速度,并且能够在最少迭代次数内找到全局最优解;其次是LM-MEA算法.在Sphere函数优化中,LM-PSO算法只用了30次迭代就找到了全局最优解;而LM-MEA算法和LM算法分别需要80次和150次迭代才能找到最优解.在Rosenbrock函数优化中,LM-PSO算法只用了130次迭代就找到了全局最优解,比LM-MEA算法少用了45次.同时,本文提出的LM-PSO-DTW算法在人体动作捕捉方面的准确率最高.该算法对肩部推举、阿诺推举和深蹲这3个动作的识别准确率也相当高,分别达到97.81%,98.01%和99.35%;相较于AS-GCN算法准确率分别提升了3.28%,6.67%和6.49%.随着测试距离增加,各个算法的动作捕捉准确率呈现出先增后减的趋势.在测试距离为3 m时,各算法的准确率达到最高.在这个距离下,LM-PSO-DTW算法的动作捕捉准确率高达99.35%,比AS-GCN、SAT-GTCN算法分别提高了7.24%,4.01%.随着测试角度增大,各个算法的动作捕捉准确率呈现出下降趋势,表明本文所提出的算法具有很强的实际应用性,有助于现代各个领域的人体动作捕捉及动作矫正.但实验中的动作设计较少,未考虑复杂动作的捕捉与评估,后续的研究可考虑引入更多的人体动作进行实验验证.



 下载:
下载: