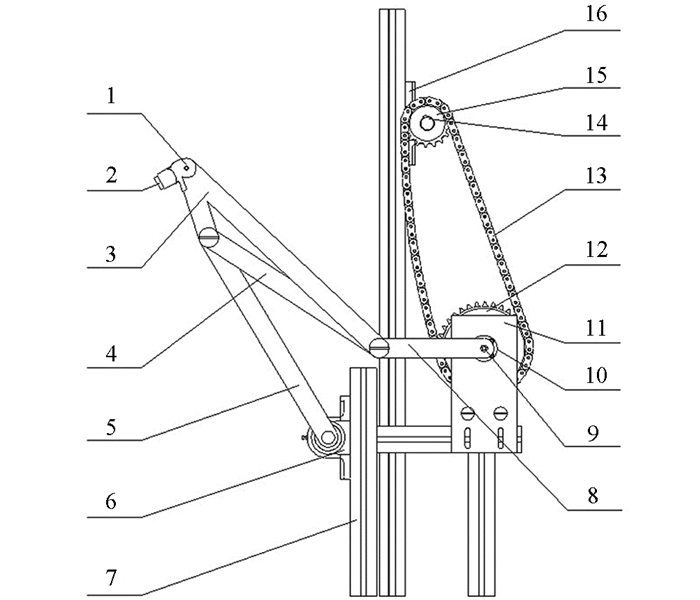
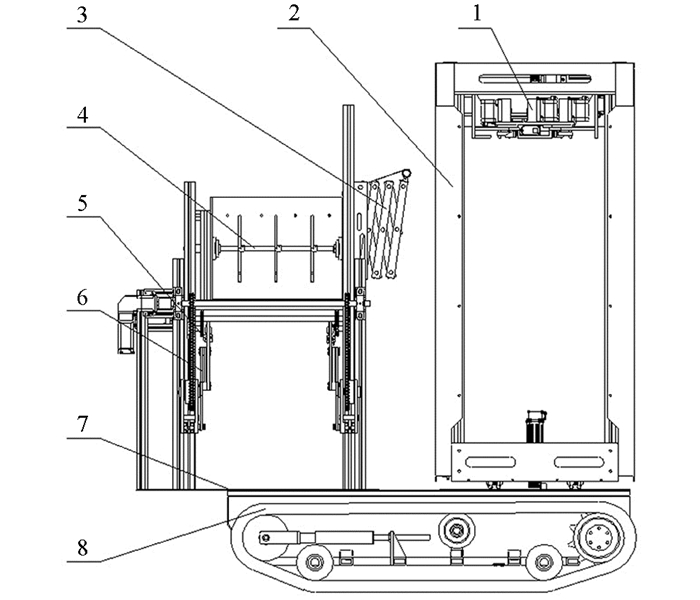
我国大部分桑园位于丘陵山地，行宽为2 m，坡度为0°~25°，因此采用履带式底盘作为桑叶自动采收机的行驶工具. 丘陵山地桑叶采收机结构如图 1所示，整体装置主要由桑叶采摘装置、桑叶采摘机架、桑叶收集装置、履带车底盘组成.

桑叶收集装置包括底板、接料机构、导料机构、送袋机构和取袋机构，其中取袋机构是其核心部分，取袋机构结构如图 2所示. 当桑叶采摘装置完成桑叶采摘后，接料机构开始工作将桑叶运到收集部分. 桑叶进入料仓后，导料机构通过旋转拨料的方式，将桑叶具有方向性地转运入袋；该采摘机采用链条式送袋机构，以实现对吨口袋的定向输送；取袋机构上配置有电磁吸铁，根据吸合原理取出安装在送袋机构上的吨口袋(设有磁吸石)，吨口袋通过取袋机构运动实现袋口的展开，最终实现桑叶的采收及装袋功能.

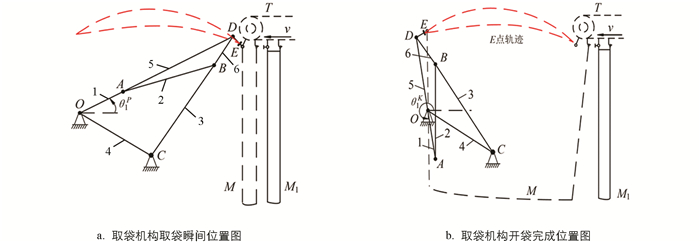
鉴于桑叶采摘收集作业环境限制，为了实现准确取袋功能及结构轻量化，本文提出了一种多连杆取袋机构，该机构由曲柄、连杆、摇杆、机架、连动杆、连动杆附杆、末端执行器电磁铁组成. 工作原理图如图 3所示，其中T为送袋机构，v为送袋方向，M为待取袋位置，M₁为待输送袋位置，θ₁^P为取袋时刻曲柄与水平轴的正向夹角，θ₁^K为装袋时刻曲柄与水平轴的正向夹角. 取袋机构的工作过程可分为取袋、开袋与装袋过程.

在多连杆取袋机构中，OC为固定机架，在图 3a取袋瞬间时刻，送袋机构T保持静止，曲柄转角为θ₁^P，末端执行器电磁铁DE在通电状态下与待取袋磁吸石相接触，实现吸合并完成取袋过程. 为保证末端执行器顺利与磁吸石贴合，在取袋时刻E点速度应尽量小. 经测试，电磁铁末端平面为斜45°时，取袋效果最佳. 通过优化取袋机构设计参数，可得到末端电磁铁在取袋瞬间极限位置DE时刻的取袋夹角最优值.

如图 3b所示，当曲柄持续旋转到θ₁^K时，曲柄停止转动并完成开袋过程. 为了确保开袋效果的平稳性，末端执行器速度幅值波动应较小. 在取袋与开袋过程中，送袋机构保持静止状态. 开袋完成后进行桑叶采收装袋. 桑叶装袋作业一定时间后，电磁铁断电，送袋机构沿着指定方向运动，使得袋口自动脱落，完成装袋过程. 曲柄继续旋转，电磁铁通电，逐渐回到图 3a取袋瞬间时刻，从而完成一次循环并开始重复作业.

在前期开袋试验后，选取型号为KK-P34/25吸盘式电磁铁作为执行件，其基本尺寸参数为圆外径34 mm、长度25 mm、吸力25 kg. 考虑电磁铁实际尺寸参数与电磁铁支撑座尺寸，最终确定末端执行器DE总长度为50 mm.

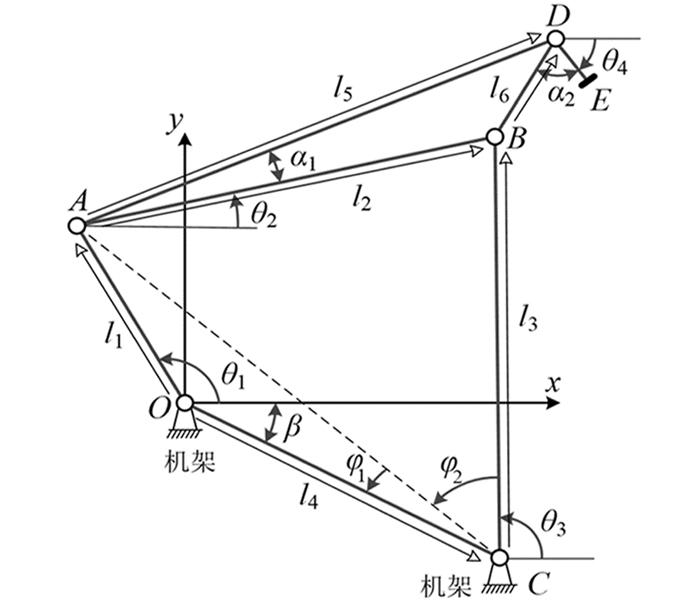
取袋机构主要由连杆运动机构与末端执行器电磁铁2部分组成. 图 4为取袋机构的运动分析图，以曲柄动力输入位置O为坐标原点，水平右方向为x轴正方向，竖直向上方向为y轴正方向建立笛卡尔直角坐标系.

根据封闭图形OABC构建解析方程为：

引入辅助线连接AC，可得：

进而求得CB杆件角位移θ₃与AB杆件角位移θ₂为：

在封闭图形ADB中可以求得D点位移方程：

式中：x_D，y_D为D点横坐标和纵坐标，mm. 其中α₁由余弦定理得到：

由几何关系可得：

由式(9)得E点的位移方程为：

式中：x_E，y_E为E点横坐标和纵坐标，mm. 在式(9)位移方程中对时间求一阶导数，得到E点的速度方程：

式中：$ \dot{x}_E$，$ \dot{y}_E$为E点横坐标和纵坐标的速度分量，mm/s.

通过对连杆长度、安装角度的合适选择与设计，可确保在有限作业空间内，更好地完成取袋和开袋过程，并确保取袋机构电磁铁在右极限位置顺利完成取袋动作. 因此对多连杆机构运动过程提出了设计要求，确定了2个设计目标：

1) 为了在限定作业空间内实现最大取袋距离，并实现多连杆机构轻量化设计，选定合适的连杆设计参数范围后，使E点在图 3中两极限工作时刻拥有最大横向位移. 为了更好地观测帕累托前沿结果，选择将最大横向平移添加负号形式表达，即用E点最小值位移减去最大值位移，计算公式如下：

式中：x_E^P为取袋时刻末端执行器E点的x轴线性位移，mm；x_E^K为装袋时刻末端执行器E点的x轴线性位移，mm；d_xE为开袋距离，mm.

2) 末端执行器电磁铁与待取袋上设置的磁吸石在取袋瞬间相互贴合，经过测试，末端取袋与水平夹角为45°时，取袋效果最佳，则有：

式中：θ₄^P为取袋时刻θ₄的角度.

通过建立机构模型与优化目标分析，确定取袋机构的设计变量为曲柄OA的长度l₁、连杆AB的长度l₂、摇杆BC的长度l₃、机架OC的长度l₄、连动杆AD的长度l₅、连动杆附杆BD的长度l₆，末端执行器DE与连杆l₆之间的夹角α₂.

1) 根据格拉霍夫定理，曲柄摇杆机构OABC需要满足杆长条件，即最短杆与最长杆的长度之和小于或等于其他两杆的长度之和，曲柄为最短杆且与机架相邻，可得：

2) 根据三角不等式，三角形ADB需要满足两边之和大于第三边，即最短杆与中间杆长度之和大于最长杆，可得：

3) 为确保装袋顺利进行并保证机构平稳性，E点在取袋瞬间与装袋时刻两极限位置的y轴坐标值之差不宜过大. 此外，末端执行器DE与连动杆附杆l₆之间的夹角α₂将决定末端执行器最终取袋时的姿态位置.

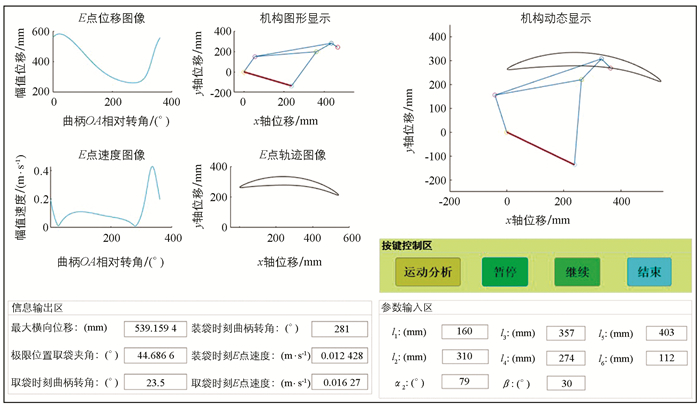
根据设计要求，基于Matlab App Designer编写了取袋机构辅助分析设计软件，界面如图 5所示. 其中包括参数输入区、图像输出区、按键控制区和信息输出区4个模块，用于分析连杆运动状态、E点轨迹图像、E点速度、合位移和关键数据输出，可简化设计过程，缩短开袋机构设计周期^[20-22]. 在设计软件中进行参数调试，当曲柄长度增大时，机构整体尺寸也会随之变大；曲柄长度太短则取袋距离过小，不满足设计要求. 为控制取袋过程中末端执行器y轴幅度不宜过大且能实现开袋最大距离，参考霍肯连杆近似直线机构，调试各杆件参数，最后确定各杆件l_i与α₂的取值范围，β取值为30°，DE由上文得知为50 mm.

带基因策略的非支配排序遗传算法(NSGA-Ⅱ)是一种全局优化算法，因其符合自然迭代规律及收敛速度较快而被广泛应用于各种优化设计领域^[23-25]. 本文采用NSGA-Ⅱ优化算法对多连杆机构的杆件长度及末端执行器安装角度建立优化模型求解，其中每个染色体代表了多连杆机构参数及末端执行器安装角度的一个设计方案，每个染色体具有交叉与变异能力(产生新染色体)，并安排其等级制度与支配关系(优胜劣汰)，以及一个目标函数(最大开袋距离与取袋角度). 父代种群中的每个个体都有突变与交叉能力，产生子代种群，同时整合种群，依据等级制度淘汰掉不够“优秀”的染色体，生成新的父代种群，从而在较短的时间内找到最优解.

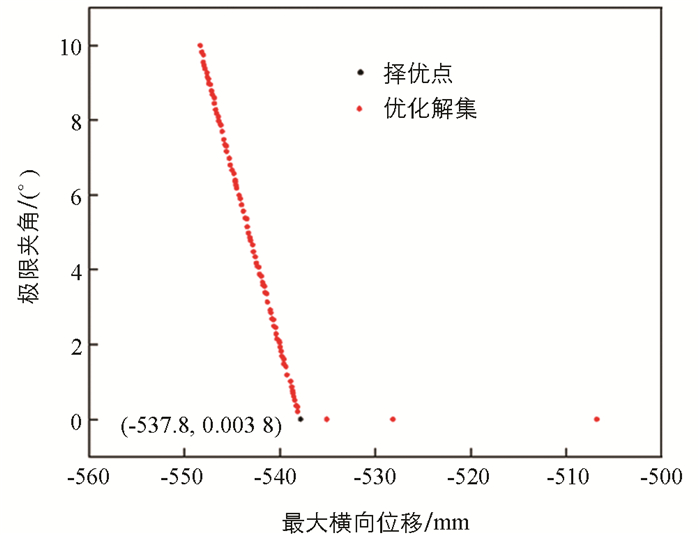
本文NSGA-Ⅱ算法的基本设置为：种群规模100、最大迭代次数600、交叉概率0.8、变异概率0.15. 所得优化解集如图 6所示.

结果显示，最大横向位移取值较大时，取袋位置夹角也偏大，两者不能同时满足. 根据设计要求，要求对取袋过程中末端执行器DE与水平之间的夹角θ₄^P更接近45±0.5°，并在此基础上保证最大横向开袋距离，综合考虑下选择取袋距离d_xE=537.82 mm，θ₄^P=44.996°的最优解. 根据实际加工条件，最终选择表 1所示实际参数结果.

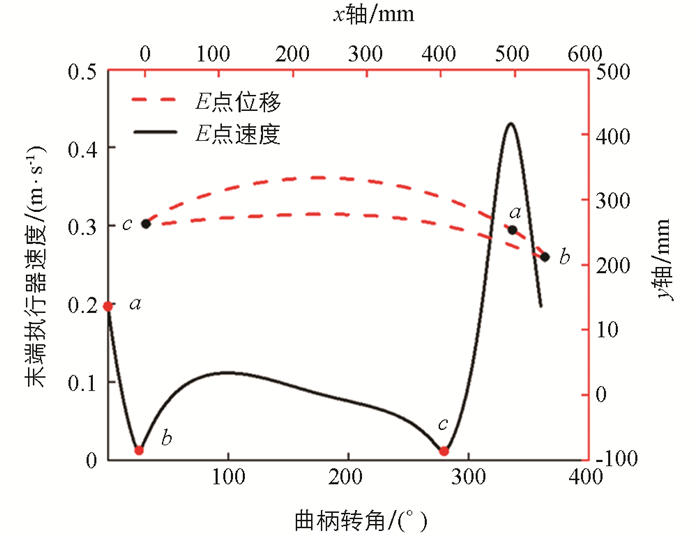
验证参数优化设计合理性，将最终得到的连杆参数输入取袋机构辅助分析软件，通过辅助交互界面得到最大取袋距离d_xE=539.16 mm，θ₄^P=44.69°，满足设计要求；得到多连杆机构姿态位置特征与末端执行器E点速度与轨迹图像，如图 7所示.

分析图 7中取袋、开袋与装袋过程. a点为静止初始位置，此时曲柄转角θ₁=0°，末端执行器位置为(496.6 mm，253.3 mm)，曲柄开始以0.1 r/s速度逆时针旋转；当旋转到b点时为取袋瞬间，达到右极限位置，末端执行器速度缓慢降到0.016 m/s，满足取袋瞬间低速要求，此时末端执行器位置为(540.8 mm，212.7 mm)，末端执行器电磁铁与水平之间的夹角为44.69°，完成取袋动作. 随后曲柄继续旋转，进入bc段，该过程为开袋过程，E点速度波动不大，符合开袋过程设计要求. 当曲柄旋转到达c点时，速度不断减小，末端执行器同时移动到最大距离，此时电磁铁的位置为(1.6 mm，263.2 mm)，曲柄停止旋转，曲柄转角为θ₁=281°，此时为装袋时刻. 最后回到cb段，即取袋阶段，此阶段利用连杆机构急回特性，可缩短取袋回程时间，提高工作效率.

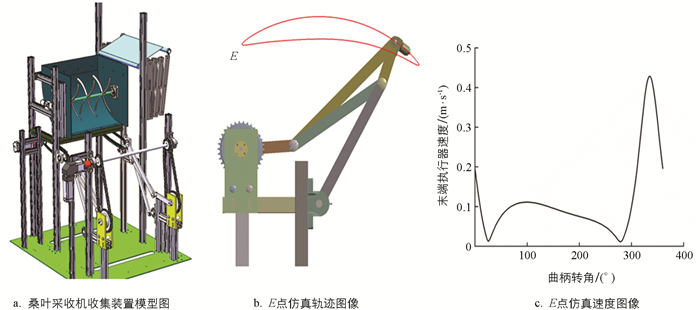
根据参数选择结果，利用SolidWorks三维设计软件建立了多连杆取袋机构的三维模型，并将装配体导入ANSYS仿真分析软件的刚体动力学模块中进行运动仿真分析. 在仿真中，设置零件之间的相关约束条件，设置动力输出轴的转速为0.1 r/s，通过仿真分析得到末端执行器电磁铁E点的轨迹图像与速度图像. 图 8为桑叶采收机收集装置三维模型与E点轨迹及速度仿真图.

比较图 7与图 8b之间末端执行器电磁铁E点轨迹图像、图 7与图 8c之间E点速度图像，可知仿真结果与理论结果基本一致，验证了多连杆取袋机构运动学模型建立的正确性和优化设计结果的合理性.

完成桑叶采收机取袋机构运动仿真验证后，加工出物理样机，如图 9所示.

基于高速摄像技术绘制出取袋机构运动轨迹，拍摄帧数设定为500 f/s，取袋机构电机选用汇川40B30CB伺服电机. 拍摄完成后在After Effects视频分析软件中进行分析，根据电磁吸铁中心点E为描绘点，E点特殊点位置与运动轨迹如图 10所示，其中a，b，c，d点分别为曲柄在静止初始位置、取袋时刻、装袋时刻、曲柄旋转180°的E点状态. 通过与E点理论轨迹图 7和仿真轨迹图 8b进行对比，发现三者轨迹基本一致.

对连杆进行x轴方向测绘，得到平均最大开袋距离数值为551 mm，误差为2.2%. 测量末端执行器电磁铁在取袋机构极限位置的角度，得到其平均数值为46.2°，误差为3.4%. 所有参数在误差允许范围内，验证了该取袋机构设计的合理性，满足桑叶收集取袋的工作要求.

根据前期准备工作与分析，曲柄转速大小决定取袋时刻与开袋过程的成功率. 转速过快，取袋与开袋过程容易失败；转速过慢，工作效率降低. 吨口袋种类的形状与大小将决定袋子在取袋机构工作过程中展开时的流畅程度与袋子脱袋情况，适配的吨口袋将决定取袋开袋的成功率. 取袋开袋过程中磁吸石与末端执行器相互作用，磁吸石外圆尺寸大小将会影响取袋时刻能否顺利完成送袋以及开袋过程是否容易脱袋. 为探究曲柄转速(A)、吨口袋形状与尺寸(B)、磁吸石外圆尺寸(C)3因素对桑叶采收机取袋机构取袋开袋效果的影响，并以较少试验次数寻求较优组合，开展取袋机构正交试验. 本次试验场地为西南大学后山桑园内，试验材料为6月份桑叶，桑叶长度约为180~280 mm，宽度约为100~180 mm. 图 11为一个完整取袋开袋过程，分别为待取袋、取袋、开袋及装袋时刻的状态.

试验以取袋开袋成功率为试验指标. 取袋开袋成功率是指取袋机构工作过程中能完成整个取袋开袋过程的概率. 取袋开袋成功率越高，桑叶收集装袋效果越好，取袋开袋成功率计算式如下：

式中：S为取袋开袋成功率(%)；Q为取袋开袋试验次数；R为取袋开袋试验失败次数.

通过前期试验与设计要求，曲柄转速取值范围为0.1~0.3 r/s；根据取袋机构的最大开袋距离为551 mm，吨口袋尺寸过小会导致开袋失败，过大会导致袋口展开后发生变形，影响装袋效果. 即可以选择方体550 mm，圆柱体600 mm*600 mm，方体600 mm 3种规格吨口袋；其中磁吸石外圆尺寸过大将会与送袋机构发生干涉，测试后得知应小于25 mm. 根据磁吸石参数标准，磁吸石可适配选择直径为16 mm，20 mm，25 mm 3个水平. 试验因素水平如表 2所示.

本试验选取L₉(3⁴)正交试验表进行试验，并添加一列空白列，在试验中每组分别完成40次取袋开袋试验以及150张桑叶转运入袋试验，每组分别完成3次取平均值，正交试验方案与试验结果如表 3所示.

由表 4和表 5可知，A因素对取袋效果表现为极为显著，B、C表现为显著，能较好地评价各试验因素与评价指标之间的参数关系，取袋开袋成功率影响的显著顺序为A＞C＞B. 结合各因素对试验指标的影响，得出最优试验因子组合为A₁B₁C₂，即曲柄转速为0.1 r/s, 吨口袋形状与尺寸为方体550 mm, 磁吸石外圆尺寸为20 mm.

为验证正交试验结果的准确性，以最优参数组合进行重复验证试验，试验结果如表 6所示. 试验结果表明，在曲柄转速为0.1 r/s、吨口袋形状与尺寸为方体550 mm、磁吸石外圆尺寸为20 mm时，平均取袋开袋成功率为97.50%，满足桑叶采收机工作要求.

本文针对丘陵山地桑叶自动采收机的取袋机构展开了深入研究，建立了取袋机构运动学模型并对其进行参数优化，最后完成仿真验证与样机试验.

1) 基于取袋原理，设计了一种多连杆取袋机构，建立了机构运动学模型并完成参数优化设计. 为了满足桑叶采收机的设计要求，基于Matlab App Designer开发了取袋机构辅助分析设计软件，并确定了机构参数的优化范围. 应用NSGA-Ⅱ非支配排序遗传算法优化了设计参数，并根据实际加工条件得到了以下结果：l₁=160 mm，l₂=310 mm，l₃=357 mm，l₄=274 mm，l₅=403 mm，l₆=112 mm，α₂=79°，最大开袋距离为539.16 mm，取袋夹角为44.69°.

2) 根据最终参数结果建立了取袋机构的三维模型，进行虚拟样机的运动学仿真分析，最后完成样机试验. 通过仿真得到了末端执行器E点的速度曲线和运动轨迹，理论和仿真结果基本保持一致，验证了运动学模型和优化结果的准确性. 进一步验证设计的准确性，开展了样机试验. 试验结果表明：在高速摄像技术下E点运动轨迹与理论和仿真基本一致. 以曲柄转速、吨口袋种类、磁吸石外圆尺寸为试验因素，取袋开袋成功率为指标开展正交试验，得到曲柄转速为0.1 r/s、吨口袋形状与尺寸为方体550 mm、磁吸石外圆尺寸为20 mm的最优组合. 以该组合进行验证试验，结果表明：平均取袋开袋成功率为97.50%，满足开袋的设计要求，证明了取袋机构优化设计的正确性，为农业桑园自动化水平的提升提供了技术支持.