-
开放科学(资源服务)标识码(OSID):

-
随着国内外一系列高水头、大容量水电站的建设,如何有效保证发电机组运行的稳定性是该领域重点关注的问题[1-4]. 水力过渡过程是指水电站发电运行过程中,水流从一种状态过渡到另一种状态的过程,是水电站重要的运行控制机制,在保证水电站满足电网负荷需求的同时,还能保证发电机组的稳定性和安全性[5]. 目前水电站水力过渡过程研究取得一定成果,但由于水力过渡过程的复杂性,其理论有待进一步研究和完善[6].
水电站水力过渡计算常采用解析法,该方法虽直观简便,但只能求出调压井最高、最低涌浪水位,不能完整描述波动的全过程[7]. 因此对水电站水力过渡全过程进行详尽的分析尤为重要. 通过研究不同控制工况下水电站引水发电系统水力过渡过程,确定调压井最高、最低涌浪水位及波动衰减周期;进而优化调压井井筒的设计尺寸,确定引水隧洞、阻抗孔口及压力钢管的最大、最小压力,并计算水击压力和机组转速升高值[8];确定机组最优关机时间和导叶关闭规律,以及增负荷时机组开机时间间隔;确定机组所需的最小转动惯量值,从而为引水发电系统布置、机组参数选取及水电站机组安全可靠运行提供技术参考[9-10].
本文以腊寨水电站为例,采用特征线法建立水力瞬变模型,分析该水电站有压引水系统水压、调压井的涌浪水位波动、导叶开度、水轮发电机组转速、电站调节保证计算、小波动稳定性等水力过渡过程,旨在验证现有水电站设计参数和导叶关闭及开启规律下,机组飞逸转速、管道水压、调压井水位波动等指标是否达到设计要求和调保计算标准.
全文HTML
-
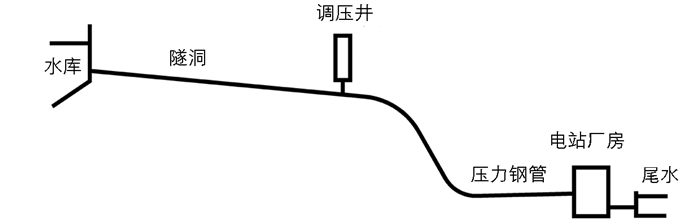
腊寨水电站位于云南省保山市龙江下游河段,正常蓄水位1 102.5 m,设计坝高68 m,总库容613.4×104 m3,电站总装机容量120 MW,年发电量6.07×108 kW·h,年利用时间5 058 h. 水电站引水系统由隧洞、调压井、压力钢管、电站厂房(水轮机)、尾水管等组成[11-14],水电站引水系统如图 1所示.
阻抗式调压井的设计参数如下:阻抗孔直径为5.2 m,主井直径为24 m,调压井底板高程为1 061 m,调压井顶高程为1 120.21 m. 厂房内安装3台混流式水轮机发电机组,水轮机型号为HLA743-LJ-312. 机组特征参数如下:设计水头为59 m,最大水头为80.5 m,额定效率为92.32%,额定流量为76.92 m3/s,转轮直径为3 120 mm,额定容量为41 MW,额定转速为200 r/min,转动惯量为3 100 t·m2. 水库校核洪水位为1 103.67 m,设计洪水位为1 103.42 m,正常蓄水位为1 102.5 m,死水位为1 090.0 m. 隧洞全长2.06 km,断面呈圆形,衬砌后洞径为8 m,喷混凝土支护的平均糙率为0.028.
-
瞬变模型由边界条件和管道水击方程2部分组成. 在该模型中,管道水击的计算采用了精度较高的特征线方法. 边界条件涵盖了水库、隧洞、管道分叉,调压井,水轮机机组等多个方面[15-18]. 通过瞬变模型可深入分析导叶开启及关闭规律,并在机组负荷变化过程中,计算调压井的水位变化、管道水压力分布、水力过渡过程等.
-
瞬变模型计算按照《水电站调压室设计规范》(NB/T 35021—2014)[5]与《水力发电厂机电设计规范》(NB/T 10878—2021)[10]中的相关规定进行.
-
在上游水库处于设计洪水位时,共用同一调压井的全部机组满载运行瞬时丢弃全部负荷作为设计工况[19];在上游水库处于校核洪水位时,相应工况作为校核标准.
-
在上游水库处于死水位时,共用同一调压井的全部n台机组由n-1台增至n台运行或全部机组由2/3负荷突增至满载作为设计工况[20],并复核上游死水位时共用同一调压井的全部机组瞬时丢弃全部负荷时的第二振幅.
-
计算调压井涌波水位,丢弃负荷时引水道的糙率取小值,增加负荷时引水道的糙率取大值. 调压井最高涌波水位以上的安全超高应不小于1.0 m,上游调压井最低涌波水位与调压井处压力引水道顶部之间的安全高度应不小于2~3 m,调压井底板应留有不小于1.0 m的安全水深.
-
当机组容量占电力系统工作总容量的比重较大,且担负调频任务时,甩负荷的最大转速升高率宜小于45%;当机组容量占电力系统工作总容量的比重不大,或担负基荷时,甩负荷的最大转速升高率宜小于55%.
-
管道的水力瞬变计算公式为:
式中:t为时间(s);H为测压管水头(m);g为重力加速度(m/s2);Q为管道流量(m3/s);d为管道直径(m);A为管道断面面积(m2);x为从管道左端起算的距离(m);f为达西沿程水力损失系数;a为水击波速(m/s).
管道的水击波速计算公式为:
式中:K为水的体积弹性模量,一般取K=2.2×109 N/m2;ρ为水的密度,大约为1 000 kg/m3;E为管材弹性模量(N/m2);D为管道内径(m);e为管壁厚度(m);c1为系数.
管道的水力瞬变运动方程可转化为下式:
管道的水力瞬变连续方程可转化为下式:
式中:Bm,Cp,Bp,Cm为t-Δt时刻的已知量;Hpi为计算断面的水头(m);Qpi为计算断面的流量(m3/s).
-
瞬变模型的边界条件包括上游水库、分叉管道、调压井、水轮机等. 边界条件的计算方法如下.
-
由于水电站调速系统瞬间变化率比水库水位的变化率大,水库水位的变化率可以忽略不计,因此可以认为上游水库水位为常数,则由式(5)可得相容性方程t时刻的隧洞进口流量:
式中:Hres为上游水库水位(m);Qp1为隧洞进口流量(m3/s).
-
对于分叉连接管道,连接处没有储存容积,在任一瞬间满足连续方程,当局部水力损失忽略不计时,每根管子的相容性方程具有以下形式:
式中:Hp为公共水头(m);Hp1,Hp2,Hp3分别为管道1,2,3的水头(m);Qp1,Qp2,Qp3分别为管道1,2,3的流量(m3/s).
-
调压井中的水流惯性和水力损失与压力隧洞中相比可忽略不计,因此可以近似假设调压井底部测压管水头等于调压井水位与阻抗孔口水头损失之和,流量与调压井水位的关系由相容性方程表示为:
式中:QT为隧洞出口流量(m3/s);BpT,CpT分别为隧洞出口t-Δt时刻的已知量.
-
1) 水轮机流量特性和力矩特性
根据水轮机综合特性曲线,可以得到水轮机流量特性曲线和效率特性曲线[21-22],水轮机单位力矩M1′、单位转速N1′、单位流量Q1′与效率η的关系为:
2) 水轮机特性的变换
在水轮机的数值计算过程中,为简化模型与提高计算效率,通常采用下式对水轮机特性进行变换处理:
式中:WH为流量函数;WB为力矩函数;y=α/αr为导叶开度相对值;q1′=Q1′/Q1r′为单位流量相对值;q1B′=Q1B′/Q1r′为常数;n1′=N1′/N1r′为单位转速相对值;m1′=M1′/M1r′为单位力矩相对值;下标r表示基准值或参考值,在一般情况下取水轮机额定参数.
3) 水轮机边界条件
水轮发电机组转动方程为:
式中:M为水轮机的轴力矩(kN·m);J为机组转动部分和水体附加的转动惯量(t·m2);Mg为发电机电磁转矩(kN·m);dω/dt为角加速度(rad/s).
式(17)可以写为下述形式:
式中:n为转速相对值;m为水轮机的力矩相对值;mg为电机电磁转矩相对值;Ta为机组惯性时间常数,s. 则Ta可以写为:
式中:GD2为机组转动惯量(t·m2);Nr为额定转速(r/min);Pr为额定功率(kW).
水轮机水头H与蜗壳进口测压管水头H1和尾水管出口测压管水头H2的关系为:
式中:A1为蜗壳进口面积(m2);A2为尾水管出口面积(m2).
通过对机组突然甩负荷的水力过渡过程研究,确定导叶的合理关闭规律[23]. 在此基础上,通过计算得到机组飞逸转速最大值、管道最大/最小水压分布规律以及调压井的最高水位,为水电站的设计提供依据.
2.1. 计算准则
2.1.1. 上游调压井最高涌波水位
2.1.2. 上游调压井最低涌波水位
2.1.3. 调压井涌波水位
2.1.4. 机组甩负荷的最大转速升高率
2.2. 管道水击方程
2.3. 边界条件
2.3.1. 上游水库
2.3.2. 分叉管道
2.3.3. 调压井
2.3.4. 水轮机
-
机组甩负荷的计算条件包括:衬砌隧洞糙率为0.014,喷锚隧洞糙率为0.024. 选择的导叶关闭规律为2段线性关闭. 假设调速器死区为0.2 s,则2段线性关闭规律为:①第1段为0.2~3.2 s,导叶开度相对值从全开y=1.0线性关闭到y=0.4;②第2段为3.2~15.2 s,导叶开度相对值从全开y=0.4线性关闭到y=0(完全关闭).
在3台机组同时甩负荷条件下,计算了以下工况的水力瞬变.
工况1:Hu=10 900 m,Hd=10 205 m(死水位)
工况2:Hu=11 025 m,Hd=1 021.75 m(设计水位)
工况3:Hu=1 103.67 m,Hd=1 028.01 m(校核洪水位)
其中:Hu为上游水库水位;Hd为下游尾水位.
-
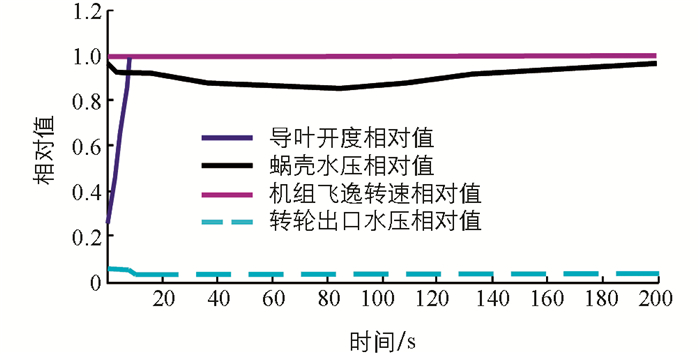
在3台机组同时甩负荷条件下,对3种工况突甩负荷进行水力计算,得到机组导叶开度、转速、蜗壳水压和转轮出口水压相对值、调压井水位瞬变值,以及管道最大、最小、初始测压管水头,并绘制相应曲线,如图 2~图 8所示. 其中Nr为机组额定转速,H0为管道初始测压管水头.
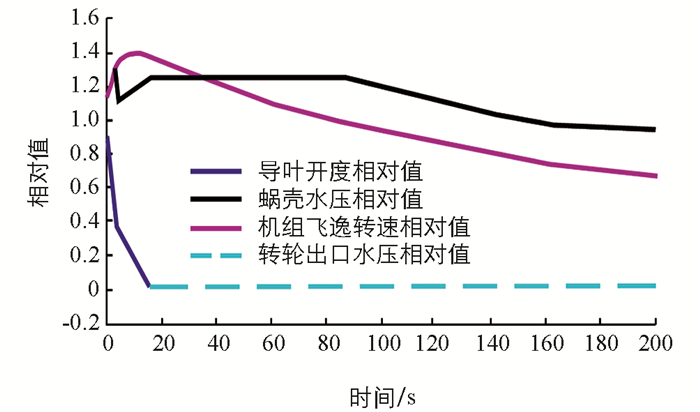
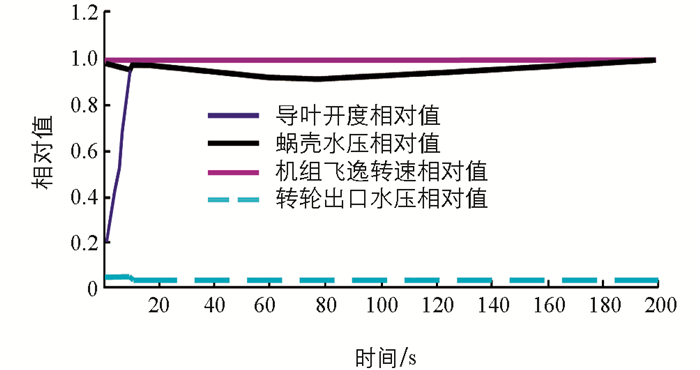
由图 2可知,在工况1下,导叶开度相对值从全开y=1.0线性关闭到y=0时,机组飞逸转速相对值迅速增大至1.40 Nr,随后机组飞逸转速相对值由1.40 Nr缓慢减小至0.64 Nr;蜗壳水压相对值迅速增大至1.28 H0,随后蜗壳水压相对值由1.28 H0缓慢减小至0.98 H0;转轮出口水压相对值变化不大.
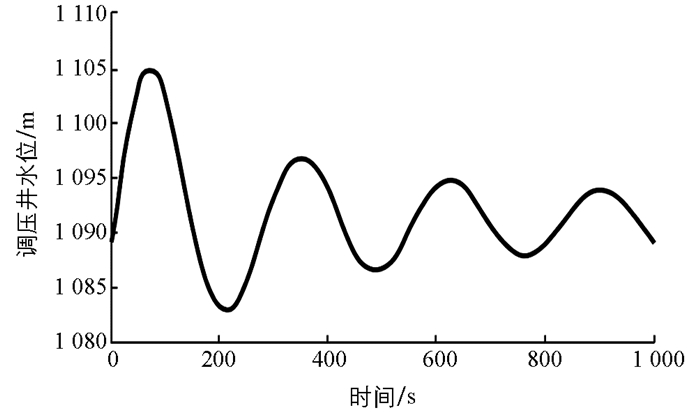
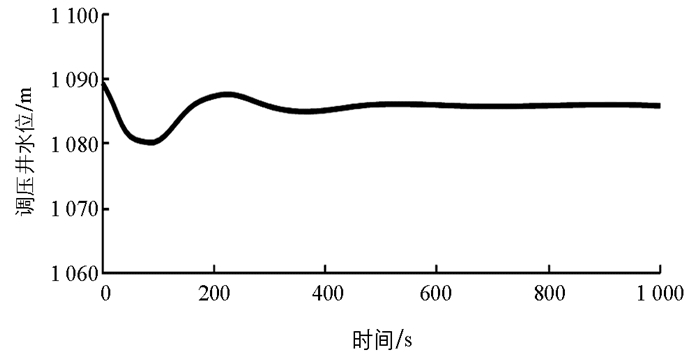
由图 3可知,当导叶开度相对值从全开y=1.0线性关闭到y=0时,调压井水位迅速增大至1 104.9 m,随后调压井水位不断上下振动衰减,调压井最低水位为1 081.8 m,最后调压井水位衰减至1 089.0 m.
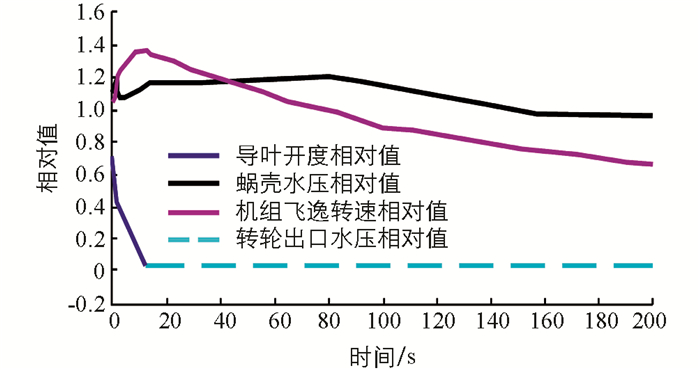
由图 4可知,在工况2下,导叶开度相对值从全开y=1.0线性关闭到y=0时,机组飞逸转速相对值迅速增大至1.36 Nr,随后机组飞逸转速相对值由1.36 Nr缓慢减小至0.64 Nr;蜗壳水压相对值迅速增大至1.22 H0,随后蜗壳水压相对值由1.22 H0缓慢减小至0.98 H0;转轮出口水压相对值变化不大.
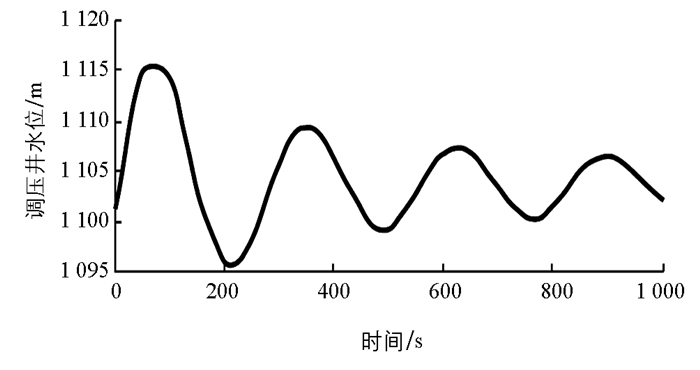
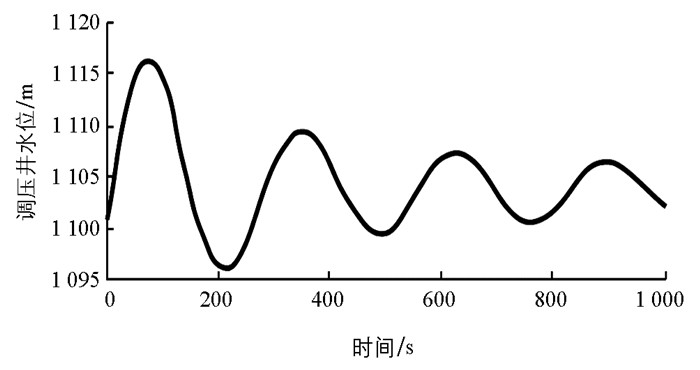
由图 5可知,当导叶开度相对值从全开y=1.0线性关闭到y=0时,调压井水位迅速增大至1 115.1 m,随后调压井水位不断上下振动衰减,调压井最低水位为1 095.1 m,最后调压井水位衰减至1 102.0 m.
由图 6可知,在工况3下,导叶开度相对值从全开y=1.0线性关闭到y=0时,机组飞逸转速相对值迅速增大至1.35 Nr,随后机组飞逸转速相对值由1.35 Nr缓慢减小至0.64 Nr;蜗壳水压相对值迅速增大至1.22 H0,随后蜗壳水压相对值由1.22 H0缓慢减小至0.98 H0;转轮出口水压相对值变化不大.
由图 7可知,当导叶开度相对值从全开y=1.0线性关闭到y=0时,调压井水位迅速增大至1 116.3 m,随后调压井水位不断上下振动衰减,调压井最低水位为1 096.2 m,最后调压井水位衰减至1 102.0 m.
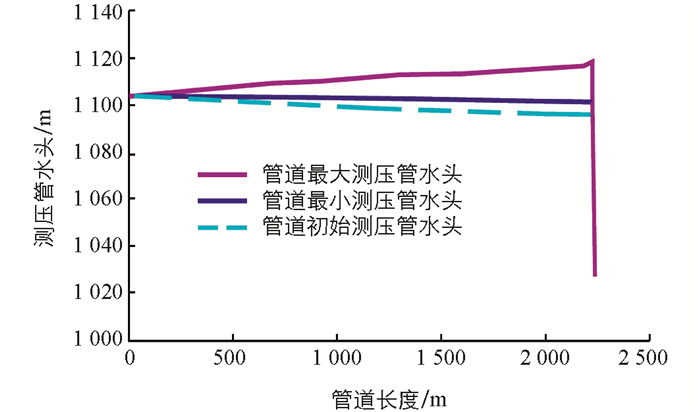
由图 8可知,导叶开度相对值从全开y=1.0线性关闭到y=0时,调压井水位迅速增大至1 116.3 m,管道测压管水头增大至1 119.0 m,随后调压井水位不断上下振动衰减,调压井最低水位为1 096.2 m,管道测压管水头衰减至1 098.0 m.
在3台机组同时甩负荷条件下,根据图 2~图 8可得甩负荷水力瞬变机组特征参数,如表 1所示.
由表 1可得以下结论:
1) 机组飞逸转速升高率
$ \frac{N-N_r}{N_r}$ ≤0.40. 机组最大飞逸转速发生在水库死水位工况.2) 蜗壳水压升高率
$ \frac{H-H_0}{H_0}$ ≤0.28. 最大水头为99.5 m,发生在水库校核洪水位.3) 调压井最高水位为1 116.3 m,发生在水库校核洪水位.
4) 随着衬砌隧洞糙率的减小,调压井最高水位随着减小.
5) 在水轮机导叶关闭及开启情况下,机组飞逸转速、管道水压、调压井水位波动均满足设计规范要求.
3.1. 计算条件
3.2. 计算结果
-
研究机组增负荷工况的目的是:①计算调压井的最低水位是否在调压井底板高程以上2~3 m;②计算引水线路最低水位是否大于大气压.
-
对于调压井而言,最低水位发生工况一般在水库死水位和最低尾水位工况. 考虑隧洞糙率的不确定性,随着糙率的增加,调压井最低水位将减小[24]. 因此机组增负荷的计算条件包括:衬砌隧洞糙率为0.016,喷锚隧洞糙率为0.028,上游水库死水位Hu=10 900 m,尾水位最低水位Hd=10 205 m.
选择的导叶开启规律是线性开启,在假设空载工况及机组并网的条件下,计算了以下工况机组的增负荷水力瞬变.
工况1:2台机组导叶全开运行,第3台机组从空载增加至满负荷.
工况2:1台机组导叶全开运行,第2,3台机组同时从空载增加至满负荷.
工况3:3台机组同时从空载增加至满负荷.
-
在机组增负荷条件下,对3种工况增负荷进行水力计算,得到机组导叶开度、转速、蜗壳水压和转轮出口水压相对值、调压井水位瞬变值,并绘制相应曲线.
由图 9可知,在工况1下,导叶开度相对值从y=0.2线性开启到全开y=1.0时,机组飞逸转速相对值变化不大,机组飞逸转速相对值在0.90 Nr附近;蜗壳水压相对值由0.98 H0减小至0.92 H0,随后蜗壳水压相对值由0.92 H0缓慢增加至0.98 H0;转轮出口水压相对值变化不大.
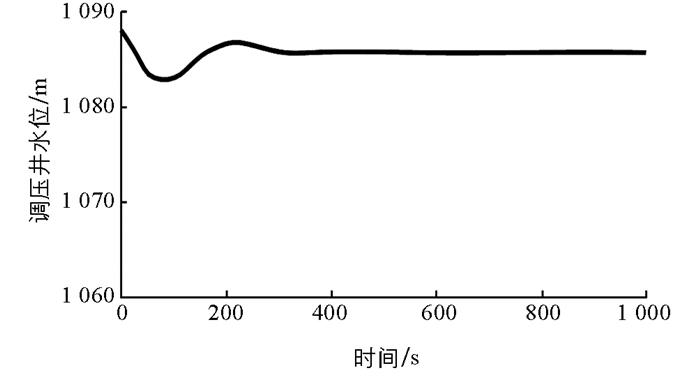
由图 10可知,当导叶开度相对值从y=0.2线性开启到全开y=1.0时,调压井水位迅速减小至最低水位1 083 m,随后调压井水位不断上升,最后调压井水位处于1 087.0 m稳定状态.
由图 11可知,在工况2下,导叶开度相对值从y=0.2线性开启到全开y=1.0时,机组飞逸转速相对值变化不大,机组飞逸转速相对值在1.00 Nr附近;蜗壳水压相对值由0.98 H0减小至0.82 H0,随后蜗壳水压相对值由0.82 H0缓慢增加至0.98 H0;转轮出口水压相对值变化不大.
由图 12可知,导叶开度相对值从y=0.2线性开启到全开y=1.0时,调压井水位迅速减小至最低水位1 080 m,随后调压井水位不断上升,最后调压井水位处于1 087.0 m稳定状态.
由图 13可知,在工况3下,导叶开度相对值从y=0.2线性开启到全开y=1.0时,机组飞逸转速相对值变化不大,机组飞逸转速相对值在1.10 Nr附近;蜗壳水压相对值由0.98 H0减小至0.80 H0,随后蜗壳水压相对值由0.80 H0缓慢增加至0.98 H0;转轮出口水压相对值变化不大.
由图 14可知,导叶开度相对值从y=0.2线性开启到全开y=1.0时,调压井水位迅速减小至最低水位1 077 m,随后调压井水位不断上升,最后调压井水位处于1 087.0 m稳定状态.
在机组增负荷条件下,根据图 9~图 14可得增负荷水力瞬变机组特征参数,如表 2所示.
表 2给出了3种工况下增负荷瞬变特征参数,得到结论如下:
1) 蜗壳水压降低率
$ \frac{H-H_0}{H_0}$ >-0.19,发生在3台机组同时从空载增加至满负荷时,蜗壳最小水头为57.2 m.2) 调压井最低水位为1 076.3 m,发生在3台机组同时从空载增加至满负荷时. 由于调压井底板高程为1 061 m,所以调压井最低水位与调压井底板高程之差大于15 m,满足设计规范要求.
3) 水轮机上游引水系统中最小水头均大于15 m,调压井最低水位均高于隧洞顶7 m以上,不会把空气带入隧洞和压力钢管中,满足设计规范要求.
4) 在水轮机导叶开启情况下,机组飞逸转速、管道水压、调压井水位波动均满足设计规范要求.
4.1. 计算条件
4.2. 计算结果
-
机组丢弃负荷后,导叶接力器按照设定的关闭速度关闭导叶,随着导叶的关闭水轮机蜗壳压力迅速升高. 在导叶关闭结束时,引水系统中的调压井水位仍处于上升阶段,由于调压井水位波动过程缓慢,其波动周期远大于水锤压力的变化周期. 当调压井水位达到最大值时,水锤压力基本消失,此时的蜗壳压力变化随调压井水位的波动而波动. 因此,实际蜗壳承受的最大压力需要在导叶关闭引起的最大水锤压力和调压井最大涌波水位引起的压力之间选择大者,从设计压力钢管和蜗壳最经济合理的原则出发,最好将蜗壳最大水锤压力升高值控制在调压井最大涌波水位附近.
机组运行的稳定性主要针对孤立运行的电站才有意义,对于电站容量占电力系统总容量较小的机组,由于机组并网后的频率由电网确定,并不存在运行稳定性的问题. 孤立运行的机组能够稳定运行,并网后则一定可以稳定运行.
-
1) 在3台机组同时甩负荷条件下,机组飞逸转速升高率
$ \frac{N-N_r}{N_r}$ ≤0.40,机组最大飞逸转速发生在水库死水位工况;蜗壳水压升高率$ \frac{H-H_0}{H_0}$ ≤0.28,最大水头为99.5 m,调压井最高水位为1 116.3 m,发生在水库校核洪水位.2) 在机组增负荷的情况下,蜗壳水压降低率
$ \frac{H-H_0}{H_0}$ >-0.19,发生在3台机组同时从空载增加至满负荷时,最小水头为57.2 m. 调压井最低水位为1 076.3 m,由于调压井底板高程为1 061 m,水轮机上游引水系统中最小水头均大于15 m,调压井最低水位均高于隧洞顶7 m以上,不会把空气带入隧洞和压力钢管中,满足设计规范要求.3) 在水轮机导叶关闭及开启情况下,机组飞逸转速、管道水压、调压井水位波动均满足设计规范要求.



 下载:
下载: