-
开放科学(资源服务)标识码(OSID):

-
作为太赫兹时域光谱检测系统(THz-TDS)的新兴成像技术,太赫兹(Terahertz,THz)成像技术近年来受到越来越多的关注. THz波频率介于0.1~10 THz之间,有极强的穿透能力,对非极性材料的探测能力使其在透射成像上能近似达到X射线扫描的效果,并且THz释放的能量很小,不会对人体产生有害的光致电离,比X射线更加安全,因此在缺陷检测、安全检测、医学检测等领域有着巨大的应用价值[1-3].
THz波长为0.03~3 mm,相比于光波和红外波波长较长,受到衍射影响较大,导致THz图像普遍存在分辨率低、边缘模糊等问题[4]. 为了提高图像质量,研究者最初将目光放在优化THz硬件设备上[5],花费大量人力物力但收效甚微. 如今随着图像处理技术的逐渐成熟,国内外学者研究重心偏向利用算法来提高图像分辨率,成本降低的同时取得了有效的成果[6-8]. 图像的超分辨率(Super-resolution,SR) 重建主要分为3种方法,分别是基于插值的方法、基于重构的方法与基于学习的方法[9-10]. 基于插值的方法主要有线性插值法和非线性插值法. 线性插值法包括最近邻插值、双线性插值与双三次插值3种,线性插值法直接通过算法拟合,实现方式较为简单,但重建出来的效果也是最差的. 相较而言,非线性插值法在SR重建上更具实用性. 郭佑东等[11]将梯度变换的方法应用于经过插值的THz图像SR重建,提高了图像质量并避免了由图像灰度剧烈变化导致的振铃现象,但非线性插值法存在计算复杂度较高,计算速度较慢,灵活性较弱的问题. 基于重构的方法主要是频域法和空域法,能够将不同场景的低分辨率图像信息进行融合得出较好的结果,计算速度有所提升且有较高的灵活度. 雷茂等[12]对凸集投影(Projections onto Convex Sets,POCS)算法进行改进并用于THz图像,峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)较原本POCS算法提升了1.02 dB,获得了质量更好的图像,但重构法的重建效果受限于放大倍数并且需要多张低分辨率图像重构,实现条件较为复杂.
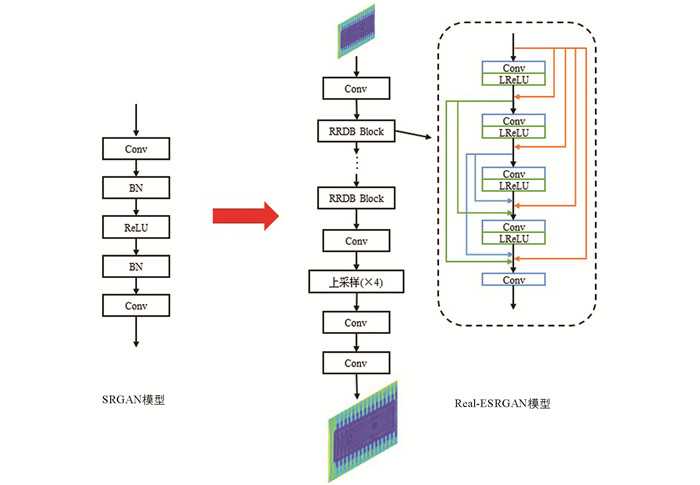
基于学习方法的超分辨率重建目前已被广泛应用于光学、电子学等领域. 基于学习的方法分为浅层学习和深度学习2种[13],目前THz图像超分领域广泛使用深度学习的方法,主要采用基于卷积神经网络(Convolutional Neural Networks,CNN)和生成对抗网络(Generative Adversarial Network,GAN)2种网络结构. CNN网络主要通过对大量低分辨率图像进行特征提取、非线性映射和重构来学习到高分辨率图像的映射函数,进而利用映射函数进行SR重建. 卢贺洋等[14]在CNN网络基础上对残差网络进行改进,加深网络结构,在THz人体安检图像上取得了较好的超分辨率结果. CNN网络进行SR重建工作大都以获得更高的PSNR值为导向,认为PSNR值越高表示图像重建的效果越好,导致模型生成的图像过于强调低频信息的重建,损失掉了高频细节信息,实际得到的SR图片观感上的提升较弱. Ledig等[15]提出了SRGAN模型,首次将生成对抗网络用在了SR问题上,利用生成器和判别器进行对抗训练,得到低分辨率图片到高分辨率图片的映射函数,根据训练模型对导入的低分辨率图像进行预测并重建出高分辨率图像,实现了感观上的明显提升,更符合图像SR的实际需求.
现有的THz图像SR方法多侧重于在网络结构上的改进[16-17],而忽略THz光谱采集过程中存在的环境噪声、复杂系统噪声等干扰问题,如双三次插值降采样所得到的训练模型用于THz图像时往往达不到预期质量的提升. 针对上述问题,本文对采用单一频率成像的THz图像展开研究,引入Real-ESRGAN模型[18],对含不同干扰信号影响的THz低分辨率图像展开SR重建研究,分析初始输入不同干扰信号图像对不同SR模型结果的影响,同时验证该模型在THz图像SR领域的潜在价值. 本文中THz成像、图像增强、SR重建及评价的简要流程如图 1所示.
全文HTML
-
本次试验选择美国API公司推出的T-Ray 5000太赫兹时域光谱检测系统,设备原理图如图 2所示. 该系统采用光电导天线产生和探测THz波,发射器和探测器之间的光程约为30.8 cm;采用钛蓝宝石激光器作为超短脉冲发射光源,所产生的飞秒激光中心波长为1 064 nm,输出脉宽为80 fs,重复频率为100 MHz,输出功率为20 mW,可支持80 ps的时间扫描范围,时间分辨率为0.1 ps,有效频谱范围为0.05~3.5 THz,频谱分辨率为12.5 GHz. 二维扫描移动台平面最大可支持30 cm扫描范围,扫描步长最小为0.1 mm.
-
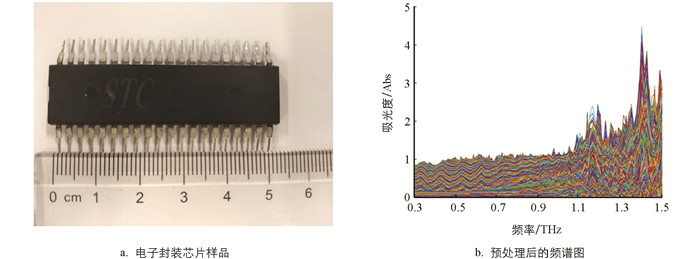
试验待测样品选择STC89C51单片机的内部电子封装芯片,如图 3a所示. 将样品置于二维扫描平台进行透射成像,扫描步长为0.25 mm,扫描速度为50 mm/s. 试验选择在超净间进行,保证外界环境的温度恒定,湿度相对较低,减少试验环境对THz设备扫描结果的影响. 由于时域信号同时携带较多噪声信号,成像效果较差,无法有效表示样品特征,故选择在频域上对样品进行成像. 通过傅里叶变换得到样品的频域光谱数据集,为判断频域最优成像区间,综合光谱预处理方法结果,选择SG平滑去噪和airPLS基线校正进行预处理,如图 3b所示. 综合分析光谱数据,去掉明显含噪区间后初步选择成像区间在0.3~1.0 THz内.
分别选择4个不同频段进行成像对比,观察成像效果,图 4给出0.4 THz,0.613 THz,0.738 THz,0.988 THz 4个频段的频域成像结果. 在0.4 THz频率成像后的图片中只能观察到大致的样品轮廓,无法看到内部细节,不具备参考价值. 0.613 THz频率成像后出现了样品内部结构,但仍然无法看清外部引脚轮廓. 0.988 THz频率成像后可以看到较清晰的外部引脚轮廓,但内部引线结构被大量噪声覆盖难以观测,容易造成后续SR重建工作被错误信号干扰. 相比较之下,0.738 THz频率成像后同时兼顾了成像细节和信噪比的平衡,综合对比后选择0.738 THz作为成像频率.
-
直接采用频域信息进行THz成像的效果受到系统和环境造成的噪声干扰,不利于后续SR重建对比分析. 已知THz光束随着频率降低其发散程度更大、分辨率更低,故高频率的THz波的可携带的样品信息更丰富,但由于高频率THz波更容易被样品吸收,因此高频THz波可穿透深度和信噪比会更低,导致样品THz图像被大量噪声覆盖. 研究表明,THz光束具备高斯光束的特性,可利用高斯点扩散函数(Point Spread Function,PSF)对其进行去卷积图像恢复[19-20],故先采用THz图像增强算法对频域图像进行重建,滤除掉信号中包含的噪声.
THz成像系统对样品扫描成像的过程可以近似看作成像系统的PSF函数和样品函数进行卷积得到的结果,该过程可由下式表示:
式中:s(x,y)为THz系统输出的结果;P(x,y)为成像系统的PSF函数;o(x,y)为样品真实图像;n为扫描过程环境和设备导致的噪声. 获得样品真实图像的过程就是一个去卷积的过程,由下式表示:
THz系统的PSF模型函数可由下式表示:
式中:k由截断比和辐照度决定;NA为系统数值孔径;f为THz波某一频率;c为真空光速;α为样品的吸收系数;ρ为光斑半径.
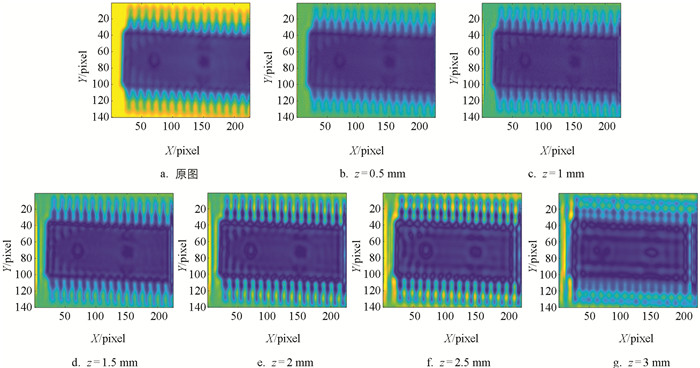
增强后的图像质量直接受PSF函数的影响. 通过构建不同光束穿透深度z的PSF函数,可得到不同的THz增强图像,结合高斯光束理论和去卷积算法对样品THz图像进行增强. 本文所选样品厚度为3 mm,共构建了6个不同深度z的PSF函数进行对比分析,结果如图 5所示.
初步对比图像质量,可发现当z的深度设置为2 mm时,图像的效果较好,芯片引脚及内部引线显示更加清晰;当z的深度设置为2.5 mm时,图像效果较好但出现了少量伪影;其余深度下发生了特征显示不明显(z<2 mm)和图像失真较严重(z>2.5 mm)等情况.
-
客观评价标准选用像素点个数乘以步长来计算引脚宽度和引脚间距以及内部引线间距,通过与被测样品的实际引脚间距和宽度进行比较,结果越接近真实值则表示图像质量越好.
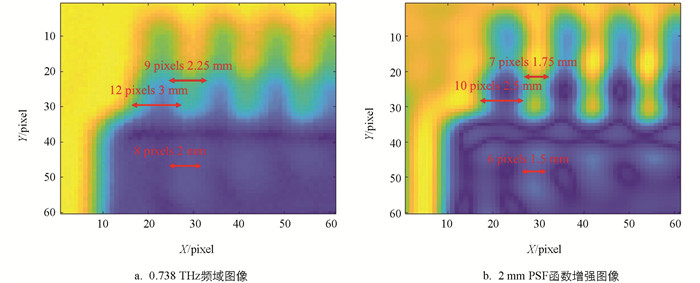
如图 6所示,取光束穿透深度z=2 mm图像和原图像的部分像素点进行放大对比,分析图像细节显示能力.
测量样品外部引脚间距为1 mm,引脚宽度为2 mm(图 6). 每个像素点间距为系统扫描步长0.25 mm,原始图像计算得引脚间距为2.25 mm,引脚宽度为3 mm. 增强图像计算得引脚间距为1.75 mm,引脚宽度为2.5 mm. 分析结果可知通过构造THz系统的PSF函数去卷积之后的图像具有更强的细节显示能力,更接近实际样品状态.
1.1. 试验设备
1.2. 试验及数据处理
1.3. THz图像增强
1.3.1. 构建点扩散函数
1.3.2. 图像质量客观分析
-
由于高分辨率THz图像采集时间过长且受限于THz设备硬件条件无法做到真正的高分辨率,短时间采集的THz图像分辨率太低无法清晰表征样品细节,因此考虑通过SR深度学习算法直接从低分辨率THz图像上重建出高分辨率的图像,本文采用一种Real-ESRGAN网络模型对THz图像进行SR重建.
-
GAN网络主要由2部分组成,分别是生成器G(Generator)和判别器D(Discriminator),G网络生成随机噪声图片作为判别器的输入,D网络负责判别生成器输入的图片是实际输入图像还是生成器产生的伪造图像.
GAN模型的目标函数如下式所示:
在上式中,G网络最终是希望D(G(z))能够趋近于1,D网络最终是希望D(x)趋近于1,生成器和判别器互相反馈结果. 二者在训练过程中不断“对抗”,通过固定一方的值去更新另一方网络的参数,使得双方参数不断迭代变化,从而使生成器产生的图片与真实图片之间的差异达到最小.
-
SRGAN网络是在深度残差网络(Residual Network,ResNet)基础上进行改进的网络,将GAN网络运用到超分辨率上,同样由生成网络和判别网络2部分组成,生成网络使用SRResNet网络,其目的是重建出超分之后的图像,判别网络与GAN类似,其目的是判断图片真假. 过去的SR问题都是基于MSE的损失函数,造成高频信息丢失从而观感提升不明显,因此研究者提出了损失感知函数(Perceptual Loss Function),可由下式表示为:
上式包括3个部分,第1部分(lXSR)为内容损失,第2部分(10-3lGenSR)为对抗损失,第3部分(2×10-8lTVSR)为正则化损失. 将内容损失函数替换为VGG(Visual Geometry Group)网络,表示为下式:
式中:Øi,j表示VGG网络j层卷积后与i层最大池化层前的feature map输出;Wi,jHi,j表示feature map张数.
-
相比于SRGAN网络,Real-ESRGAN网络主要进行了以下几个方面的改进:
1) 提出了一个数据高阶退化的过程来获取更接近真实图片的低质量图像. 不同于传统的依靠插值法直接得到LR图像,该算法模拟了更加符合真实世界噪声影响下得到的LR图像过程,通过除污(Blur)、添加噪声(Noise)、下采样(Downsampling)、JPEG压缩对HR图片进行处理生成LR图片,将LR图片输入到生成器中获得更高分辨率的SR图片,最后通过判别器对SR图片进行判别来确定图像质量好坏. LR图片获取过程如图 7所示.
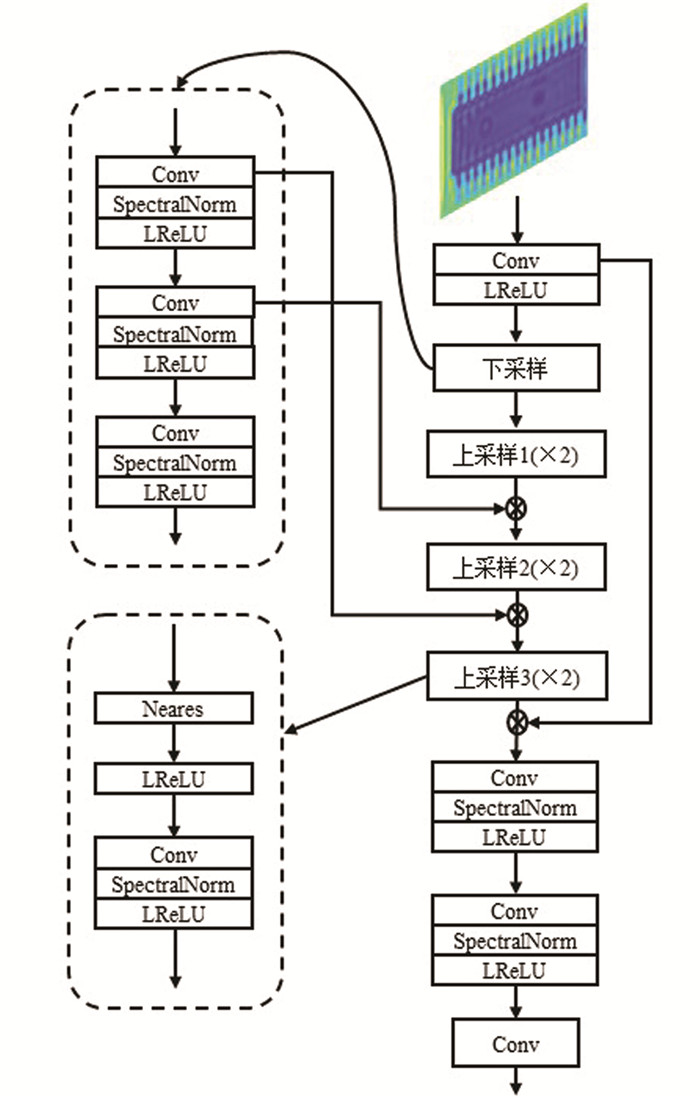
2) 在生成器网络结构上,采用了RRDB(Residual-in-Residual Dense Block)作为新的主干网络,可以获得输入图片更加深入的结构. 该网络删除了SRGAN中的BN (Batch Normalization)层,提高模型泛化能力并且使用了残差缩放减少伪影. 生成器网络结构如图 8所示.
3) 将判别器改为使用具有更强鉴别能力的U-Net代替VGG网络加强对图像细节的对抗学习,并引入谱归一化方法来缓和训练不稳定的情况. 判别器网络结构如图 9所示.
2.1. 生成对抗网络
2.2. SRGAN网络
2.3. Real-ESRGAN网络
-
采用客观评价指标验证图像重建质量,客观评价标准选用有参考图像和无参考图像2种方式验证,有参考图像质量评价选择峰值信噪比(PSNR)和结构相似度(SSIM)作为综合评价指标来评价图像重建效果,参考图像选择2 mm穿透深度构建的PSF增强函数重建图像,将SR重建结果与参考图像进行对比计算出PSNR和SSIM值.
PSNR的计算由下式表示:
式中:EMSE为均方误差MSE的值,由下式表示:
式中:X为SR重建之后的图像;Y为原始参考图像;H为图像高度;W为图像宽度;n为像素的bit数. PSNR值越大图像失真越小.
SSIM的计算由下式表示:
式中:μa为重建图像的均值;μb为参考图像的均值;σ为标准差;C1和C2为2个经验常数. SSIM取值范围为0~1,结果越接近1,则两张图片越相似.
无参考质量评价选择平均主观得分(Mean Opinion Score,MOS)[21]作为视觉主观感受综合评价指标来评价图像重建效果,采用在221张YouTube UGC Dataset截图上打分作为评分模型,评分范围为0~1,分数越高代表图像美学质量越好,越符合视觉感受的提升.
-
由于受到THz激光源条件约束,逐点扫描得到的THz图像分辨率难以提升,当想要获取样品细节信息时,往往精确度不高,因此,本文采用Real-ESRGAN方法对THz增强图像进行4倍放大超分辨率重建,采用DF2K数据集进行模型训练. SR结果如图 10所示,在不添加人为干扰的情况下,对原始的THz增强图像所得到的SR图像进行测试,客观评价指标显示,其PSNR值为26.886 dB,SSIM值为0.913 5,MOS值为0.643 6. 观察成像结果,初始图像分辨率为225×140,像素点间距为0.25 mm,放大后的图像分辨率为900×560,像素点间距为0.062 5 mm,将原图与SR图像进行对比分析,SR之后的图像引脚间距和引脚宽度更接近实际样品信息,且内部沉孔显示更加清晰,更有利于分析样品内部信息,证明了该超分辨率方法在THz图像处理上的有效性.
-
为验证本文引用算法在含噪THz图像SR重建任务中的有效性,分别使用了SRResNet、EDSR 2个CNN模型和SRGAN、ESRGAN 2个GAN模型与Real-ESRGAN统一进行对比,均采用在公开数据集训练得到的预训练模型进行超分重建任务.
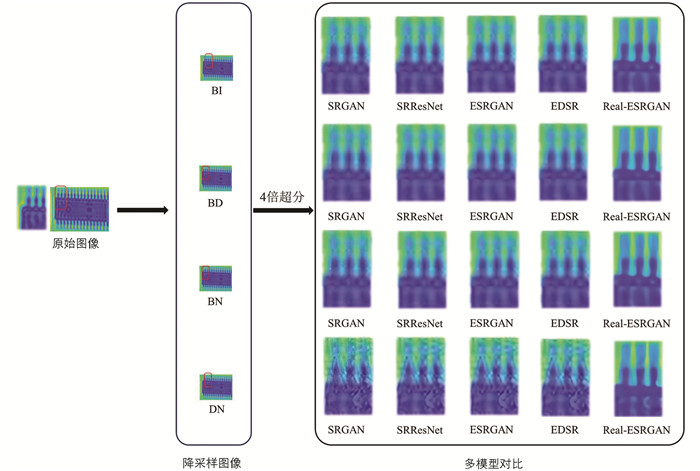
选取光束穿透深度z =2 mm去卷积图像作为参考图像. 由于THz系统成像质量可近似为受到高斯模糊及高斯噪声影响,为了模拟符合自然情况下采集的低分辨率THz图片,分别采用双三次插值降采样(BI)、高斯模糊下采样(BD)、双三次插值下采样+高斯白噪声(BN)、高斯模糊下采样+高斯白噪声(DN) 4种方法在Matlab软件上对参考图像进行四分之一缩小后得到输入LR图像,再通过5种SR重建方法对LR图像进行4倍放大,结果如图 11所示. 观察外部封装引脚显示情况,模型面对不同程度的干扰信号,Real-ESRGAN结构得到的图像相对于其他结构在边缘清晰度上有所提升,虽然在引脚部位发现仍然存在虚影,但模糊程度有了一定的降低,且平滑噪声效果更强,图片模糊程度相比于其他算法明显减少,整体观感更贴近实际参考图像.
重建图像综合评分指标计算结果如表 1所示. 以3.2节评价结果为参考,在进行BI、BD、BN、DN 4种降采样方式处理后,Real-ESRGAN方法进行SR处理后的THz图像各方面评价指标有所下降,但是对比其他4种SR算法在降采样处理之后的THz图像SR重建结果,Real-ESRGAN方法的PSNR、SSIM、MOS 3个指标值均优于其他算法. 在有参考图像质量评价结果中,随着不同程度干扰信号的加入,Real-ESRGAN在其影响下的稳定性也优于其他网络结构,PSNR值变化范围仅在0.8 dB左右,其他模型变化范围均在1.2 dB左右. SSIM值变化范围仅在0.02左右,其他模型变化范围均在0.13左右. 同时综合观察结果可以发现,对深度学习的SR重建任务影响最大的干扰信号方式为高斯模糊下采样方式,其次为高斯白噪声方式.
3.1. 评价指标
3.2. THz图像SR重建结果分析
3.3. 降采样图像SR重建结果分析
-
本文结合THz图像去卷积算法对样品的THz图像进行了图像增强,重构出THz扫描图像内部结构,滤除了高频THz波成像结果中的噪声,显示了更加丰富的内部细节. 基于此增强的THz图像,采用Real-ESRGAN算法对其进行4倍SR重建,将THz图像的分辨率从225×140放大到900×560,增强了图像细节显示能力,实现了较低采样点的个数构建高分辨率的THz图像. 同时通过试验对比,结合PSNR、SSIM、MOS 3个指标验证了Real-ESRGAN算法对THz图像质量提升的有效性. 对THz增强后的图像探索了不同干扰信号对SR任务的影响,试验结果表示,针对实际情况中通常会受到多方面噪声干扰采集到的THz图像,Real-ESRGAN所提出的高阶退化模型可以更有效地应对这一问题,也为后续THz图像SR重建技术提供了一种新的优化思路.




 下载:
下载: