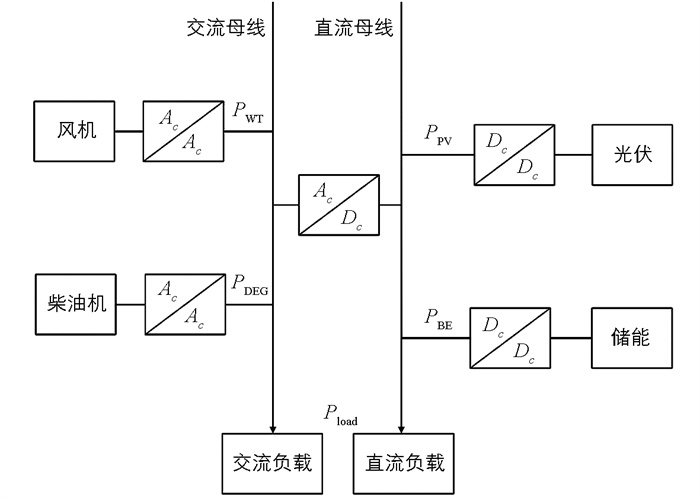
结合柴油发电机特点设计的交直流微电网结构如图 1。随着对可再生分布式能源的利用与发展，不同类型的负荷迅速增加，交直流微电网的发展受到了重点关注。交直流微电网包含直流母线和交流母线，可以同时给交流负载和直流负载供电，能够减少电能变换器的数量。交直流微电网也结合了交流微电网和直流微电网的优点，降低了电能变换的损耗，提高了微电网的可靠性，成本大大降低。

风力发电机组的发电功率取决于风速v，本研究风力发电机组的输出功率P_WT满足：

式中：ρ为空气密度；A_r为风力发电机组叶片面积；C_p是风力发电机组的功率系数。

本研究光伏发电系统的输出功率P_PV满足：

式中：η为光伏阵列的转换效率；S为光伏阵列的面积；Φ为太阳辐射强度；T_a为环境温度。

定义$ \boldsymbol{x}(t)=[\Delta f, \Delta P, \Delta p]^{\mathrm{T}} \in \mathbb{R}^n$为状态向量，$ \boldsymbol{u}(t) \in \mathbb{R}^{m_1}$为交直流微电网系统的控制信号，$ \boldsymbol{w}(t)=\boldsymbol{w}_{\mathrm{WT}}(t)+\boldsymbol{w}_{\mathrm{PV}}(t)+ \boldsymbol{w}_{\text {load }}(t) \in \mathbb{R}^{m_2}$是源荷扰动，那么源荷扰动下的交直流微电网系统模型可以被描述为：

其中具体的状态空间方程参数为：

式中：Δf表示频率偏差；ΔP表示涡轮功率；Δp表示调速器位置值；w_WT、w_PV、w_load分别表示由风机、光伏以及负载引起的功率变化；T_p表示交直流微电网系统的时间常数；k_p表示交直流微电网系统的增益；T_t表示涡轮机的时间常数；T_g表示调速器的时间常数；s_p表示调速系数。

随后对交直流微电网模型进行离散化，得到其离散模型：

从交直流微电网的模型中可以发现，风能、光伏发电以及负载功率的变化都会引起系统频率的变化。频率的稳定性是评价交直流微电网系统质量和性能的重要指标，因此需要设计一种鲁棒的LFC方案来实现交直流微电网系统频率的稳定。

H_∞控制广泛用于减弱扰动对动力系统性能的影响，对于式(4)中的交直流微电网离散模型，当其满足：

时，交直流微电网系统的L₂增益小于等于γ。

定义交直流微电网系统的H_∞控制目标：找到一个控制信号u，使得：

① 当w=0时，系统渐进稳定。

② 满足扰动衰减调节，即系统的L₂增益小于等于γ。

H_∞控制问题与零和博弈问题有很大的联系，而求解线性系统的博弈代数黎卡提方程(GARE)可以找到零和博弈问题的解。目前大部分求解GARE的方法需要完整的系统动力学知识，而在实际应用中，很多情况下我们无法得到完整的系统动力学知识，故而需要无模型的算法来求解H_∞控制问题。

常规Q学习算法虽然在求解最优控制策略和最坏扰动时无需系统动力学知识，但算法中每次迭代过后都需要通过更新后的控制策略来产生输出和扰动，在实际情况下难以保证在迭代过程中每一次更新的策略都是稳定的，而且常规的Q学习算法要求扰动按照期望进行调节并应用于系统动力学以收集数据，这在实际应用中不符合物理条件，扰动是独立的，无法按照指定的方式进行更新，因此考虑对常规Q学习算法进行改进，源荷扰动下的交直流微电网离散模型式(4)重写为：

其中A_k= A -BK₁^j-DK₂^j。

依据式(6)定义目标策略：$ \boldsymbol{u}_k^j=-\boldsymbol{K}_1^j \boldsymbol{x}_k, \boldsymbol{w}_k^j=-\boldsymbol{K}_2^j \boldsymbol{x}_k$，目标策略作为算法正在更新和迭代，而u_k、w_k则作为行为策略，实际应用于系统动力学以收集数据，因此作用于系统的扰动w_k无需按照期望进行调节。

那么贝尔曼方程为：

考虑函数V (x_k)在x_k+1处进行泰勒展开：

考虑式(8)并结合式(7)得到：

然后结合式(6)，将式(9)重写为Kronecker积的形式：

令：

其中:

而且有：

那么可以求解L₁~L₇：

需要注意的是，使用最小二乘法求解L₁~L₇需要至少N₃≥n²+m₁²+m₂²+2m₁m₂+n(m₁+m₂)数量的数据集。

依据L₁~L₇求解目标策略K₁^j+1、K₂^j+1：

离线策略无模型的Q学习算法求解目标策略无需系统动力学知识，且将目标策略与行为策略分离开，行为策略直接作用于系统用于收集数据而不参与更新，目标策略并不直接作用于系统也可根据收集的数据进行迭代更新，那么系统扰动即行为策略无需按照期望进行调节。

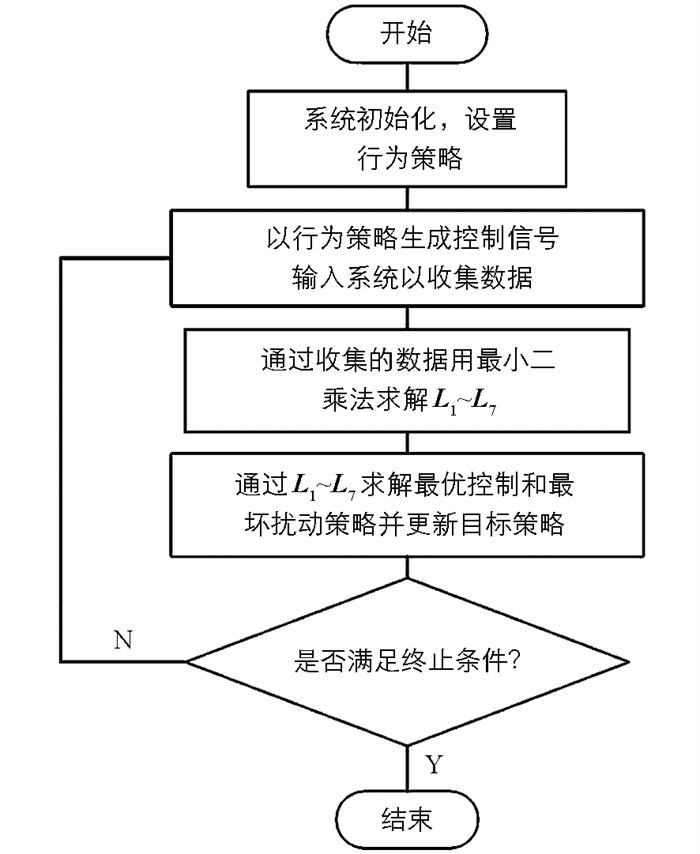
离线策略无模型的Q学习算法的具体流程如图 2。

算法流程：

① 初始化行为策略K₁、K₂，目标策略K₁^j+1、K₂^j+1设置j=0。

② 将行为策略K₁、K₂作用于系统，收集数据。

③ 策略评估：依据式(11)用最小二乘法求解L₁~L₇。

④ 策略改进：依据式(12)用L₁~L₇得到目标策略K₁^j+1、K₂^j+1，更新控制和扰动策略。

⑤ 终止条件：满足|K₁^j+1-K₁^j|≤ε、|K₂^j+1-K₂^j|≤ε时停止迭代，否则返回②。

测试平台为MATLAB R2024a，测试系统采用式(4)的交直流微电网离散模型，基准系统具体的参数设置为T_t=5；T_g=0.2；T_p=2；k_p=0.5；s_p=0.5^[15]。根据具体的测试系统参数以及采样时间T=0.05 s可以得到交直流微电网的离散模型：

采用Q =diag(1，0，1)，R=0.1，γ=0.8作为算法的参数，根据离散模型以及参数值，在算法开始前先用GARE求解得到理论的最优控制策略(K₁^*)和最坏扰动策略(K₂^*)为：K₁^*=[0.139 0 0.265 9 1.511 2]

设置初始状态和策略为：

设置总周期数为800个，分为训练周期和验证周期，在训练周期内向控制信号添加探测噪声，在验证周期内训练得到的策略进行系统控制。利用本文提出的改进Q学习算法与常规Q学习算法分别进行最优控制策略和最坏扰动策略的求解。对于常规Q学习算法每一轮迭代至少需要收集15组数据用于求解，对于改进Q学习算法每一轮迭代至少需要收集19组数据用于求解L₁~L₇，本研究设置两种算法每一轮迭代都收集20组数据用于求解，那么总迭代轮次为40轮，设置训练周期为400个，即训练轮次为20轮，验证周期为400个，验证轮次也为20轮。

基于式(13)中的交直流微电网离散模型，并考虑两种不同的探测噪声：

情况1：

情况2：

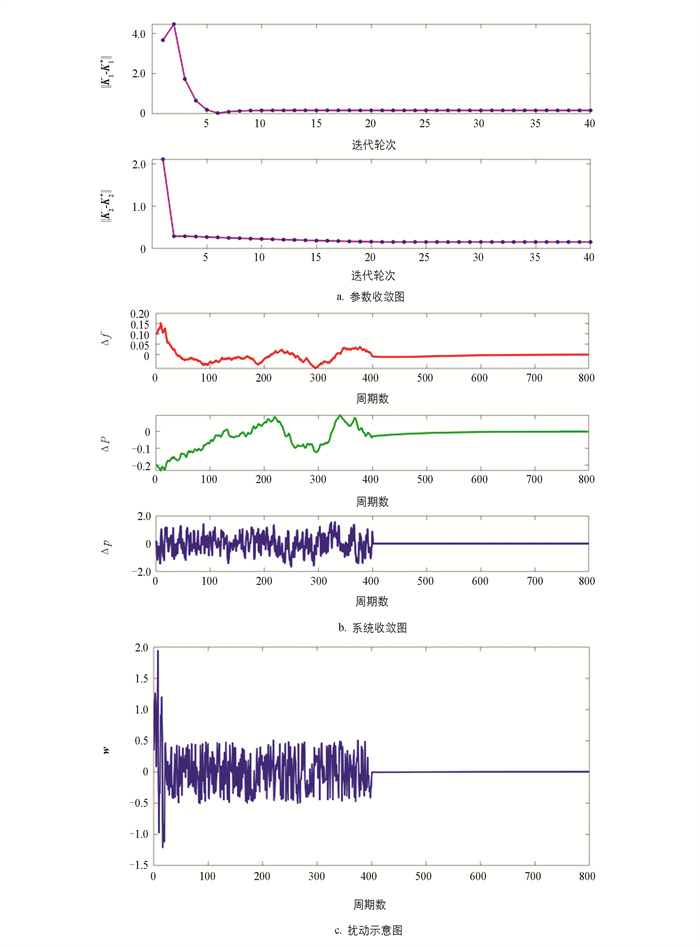
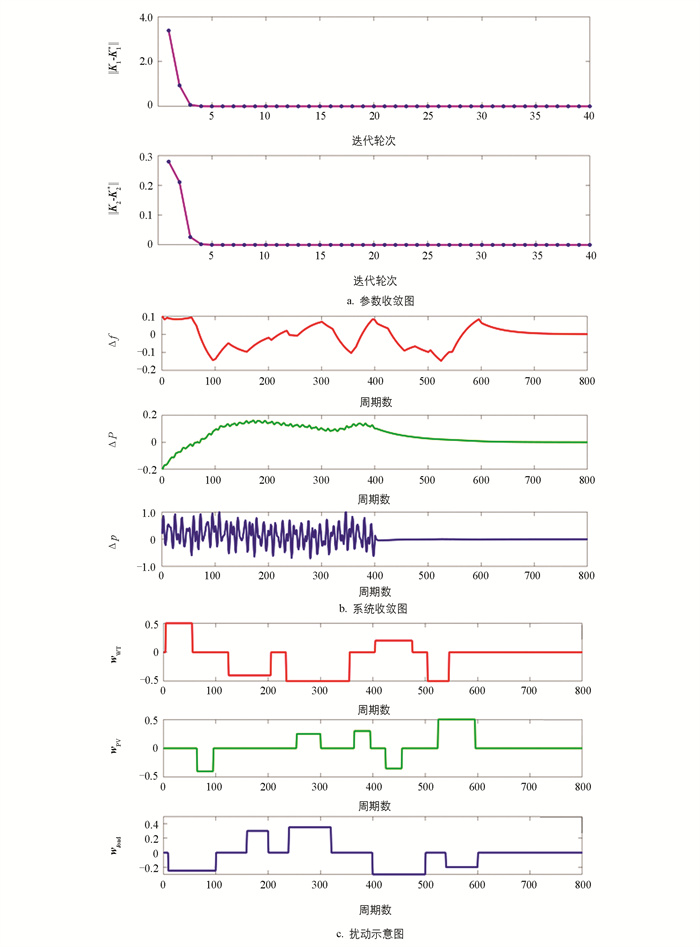
在探测噪声为情况1的条件下，常规的Q学习算法得到的结果如图 3。图 3a的参数收敛图表示策略K₁、K₂的迭代过程；图 3b中的系统收敛图则表示系统状态随周期的收敛过程；图 3c中的扰动示意图则表示系统扰动随周期的变化过程。

参数收敛图表示每一轮迭代通过策略改进计算得到的控制策略与扰动策略收敛到理论的最优控制策略和最坏扰动策略的过程；系统收敛图与扰动示意图则表示每一个周期的系统状态与扰动的值。

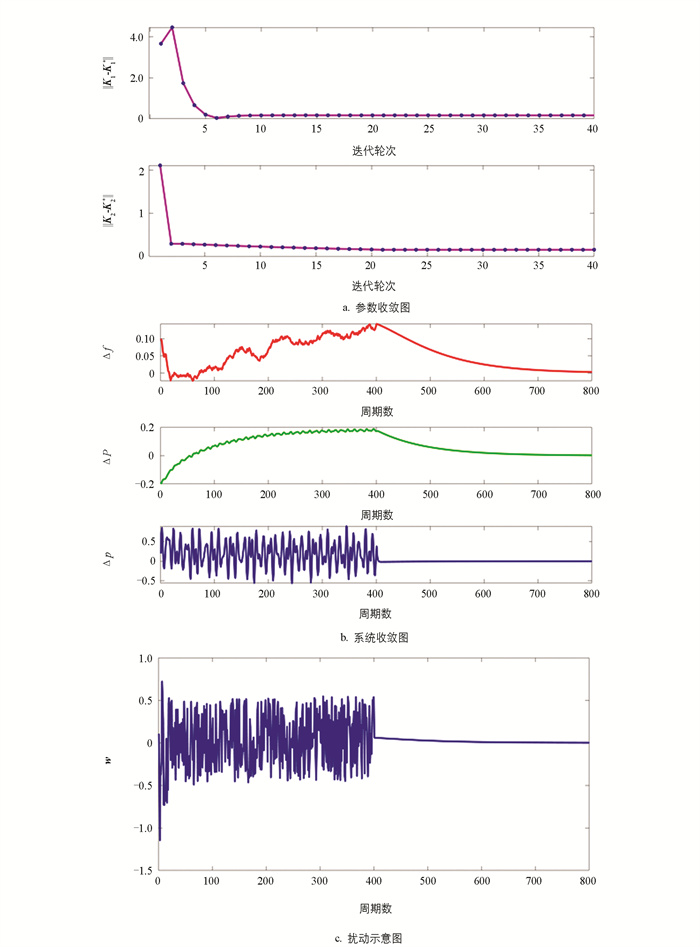
在探测噪声为情况1的条件下，改进Q学习算法得到的结果如图 4。

通过图 3与图 4中的参数收敛图可以看到，在同样的参数下，改进Q学习算法的收敛速度更快且收敛值更为精确。通过扰动示意图可以看到，在图 3c中常规Q学习算法的扰动情况是根据参数迭代情况进行调节的，而在图 4c中的改进Q学习算法是预设的真实扰动情况，无需根据参数迭代情况进行调节。

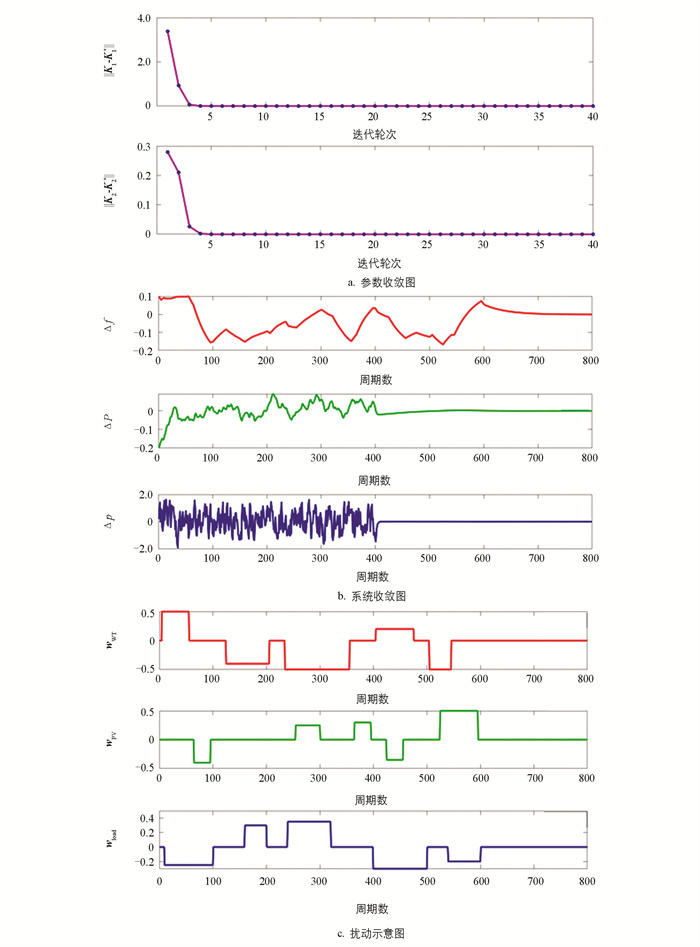
在探测噪声为情况2的条件下，常规Q学习算法得到的结果如图 5，改进Q学习算法得到的结果如图 6。

通过图 3和图 5、图 4和图 6中的参数收敛图可以看出，参数的收敛曲线探测噪声改变时几乎不会发生变化，说明算法不会受到探测噪声影响而导致错误的结果。通过两种算法的参数收敛图以及系统收敛图可以看出，改进Q学习算法后的收敛速度更快而且收敛精度也更高，且系统收敛后在扰动作用下可以保证系统频率偏差|Δf|＜0.2，满足性能的要求。通过两种算法的扰动示意图可以看出，当探测噪声改变后，常规Q学习算法的扰动需要根据参数迭代情况而进行调节，因而其扰动也发生了改变，而改进Q学习算法的扰动是预设的真实情况，不会随探测噪声改变而改变，说明改进Q学习算法的性能更好而且更实用。

本研究建立了在源荷扰动下的交直流微电网的系统模型，提出了基于Q学习的负荷频率控制方法，考虑到可能存在的源荷扰动情况，提出了基于离线策略Q学习的负荷频率控制策略，主要结论为：①通过对交直流微电网结构以及各分布式设备的建模与分析，得到了源荷扰动下的交直流微电网的基准系统模型。②本研究设计的方法用于解决交直流微电网的H_∞控制问题，不仅无需系统动力学知识，而且可以使扰动以真实情况进行调节。③在源荷扰动下交直流微电网系统的频率能够达到期望的性能，保证其安全运行。后续研究将考虑交直流微电网频率和电压的关系并进行电压的稳定控制，以及将Q学习算法与隐私保护法相结合设计加密控制器后对系统的影响。