-
做匀速圆周运动的物体其速度大小不变但方向时刻在改变,故其也是一种变速运动,因而存在加速度,称之为向心加速度,产生向心加速度的力称为向心力.现行高中物理人教版教材是先学习向心加速度再学习向心力.对于“向心加速度”这个物理量的大小如何计算,教材上只有“进一步分析表明”这简单几个字,便直接给出向心加速度的计算公式,详细的推导过程则出现在“做一做”的小字部分,并且推导过程运用了极限、微分等超过高中生知识范围的大学数学知识[1],使得中学生难以理解一些关键的推导步骤,从而给中学物理教学带来极大的困难.
目前演示向心力大小的实验仪器较多[2-4],而演示向心加速度大小的仪器几乎没有.文献[1]介绍的实验装置只能定性演示向心加速度的大小与哪些因素有关,不能定量演示或探究向心加速度计算式,为了帮助学生理解向心加速度公式的由来及意义,本研究设计制作了一个定量演示向心加速度大小计算公式的实验装置.
全文HTML
-
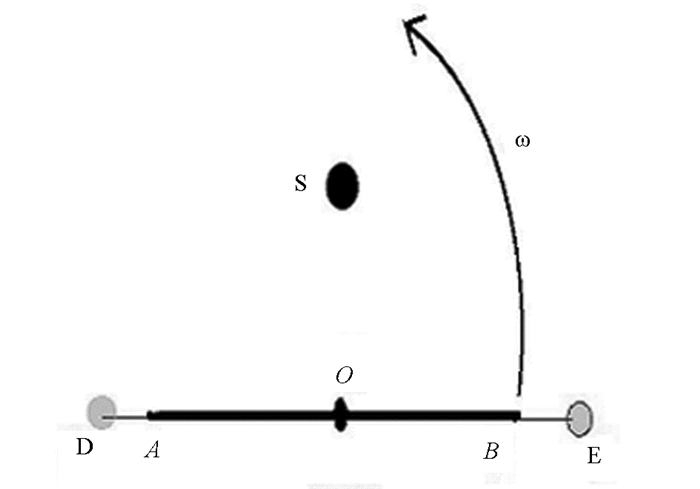
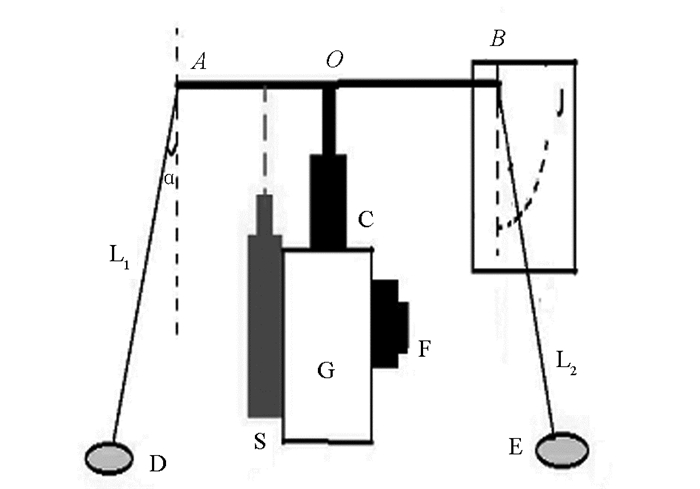
图 1中,设细软导线L1或L2的长度为l,当物体D和E在垂直于纸面的水平面内做匀速圆周运动时,圆心就在过O点的竖直转轴上,设细软导线L1或L2与竖直方向的夹角为α,通过几何关系不难得出物体D和E做圆周运动半径皆为
$r = \frac{{AB}}{2} + l\sin \alpha $ . -
运用测速器S测得杆AB的角速度大小.测速器S的原理和光电门类似,打开测速器S的开关后它将向上发射出一束红色激光,当杆AB运动到它上方的时候,杆AB下方所贴的反光纸将反射测速器S发出的激光,当测速器S接收到反射回来的激光光信号后将记次数,通过两次记次的时间间隔进行换算最终就在显示屏上显示杆AB做圆周运动的频率f.由于测速时杆AB的左右两端都会挡光,因此测速器S上显示的频率是实际频率的两倍.将测速器上显示的频率除以2,再通过频率与角速度的关系ω=2πf即可得到杆AB的角速度ω大小[1].
-
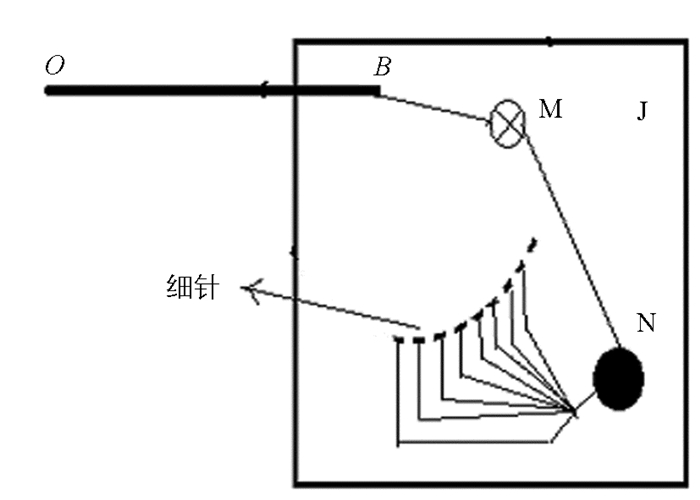
如图 3所示,在右侧杆上固定一轻质纸板J,在纸板上以杆的端点B为圆心作一段圆弧,用悬挂重物的细线过B点标定一铅垂线,与该圆弧交于点K.则圆弧上每一点与圆心B的连线均与铅垂线即竖直方向有一夹角α,在圆弧上选取一些点(在这些点很近的两侧分别插两根金属细针),这些点对应着角度α1,α2,…,可用量角器直接在纸板上分别量出与铅垂线所成角度.在纸板背面,有如图 4所示的并联电路,若导线接触到纸板上的任一根细针则其中一个支路将被接通,位于干路的小灯泡将发光.当将导线放入某两根细针之间后,物体静止时,则细导线上总有一点(H)将与细针接触而使整条细导线发生偏折成为折线,如图 3中物体处于E1位置,并且小灯泡将发光.当物体做匀速圆周运动后,导线成一条直线,如图 3中物体处于E2位置,细导线不与细针接触,小灯泡熄灭,此时该点对应的角度就为物体匀速圆周运动时导线与竖直方向的夹角α.
-
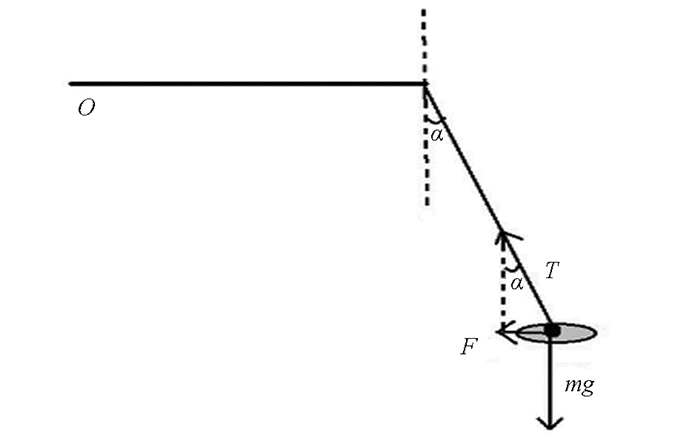
设物体的质量为m,当物体在水平面内做匀速圆周运动时,对其进行受力分析(图 5).由于物体在水平面内做匀速圆周运动,它在竖直方向上所受合力就为零,水平方向上提供向心力的合力应为F=mgtanα,式中g为重力加速度.由牛顿第二定律F=ma可得到向心加速度大小为α=gtan α,可以看出,向心加速度α的大小可以由物体在运动稳定时细导线与竖直方向的夹角α来唯一确定.因此,当调节调速器F来改变物体做圆周运动的角速度大小时,导线与竖直方向的夹角α的变化情况就对应着向心加速度α的大小变化情况.如果要验证α=ω2r的正确性,则gtan α=ω2r就该成立.将前面半径r大小的计算式代入得到ω2=
$\frac{{g\tan \alpha }}{{\frac{{AB}}{2} + l\sin \alpha }}$ ,可见一个ω对应着一个α.实验时只要测出夹角α、细导线长度l以及杆AB的长度就可以计算出角速度ω的大小.如果测速器测出的角速度ω大小与计算出的角速度ω大小相等,就验证了向心加速度大小计算式α=ω2r的正确性.
2.1. 确定运动半径的大小
2.2. 测定角速度的大小
2.3. 测定夹角α的大小
2.4. 测定向心加速度的大小
-
此装置能够定性演示向心加速度a随角速度ω和半径r的增大而增大,实验步骤在文献[1]中已经有详细介绍,下面主要介绍用实验装置定量演示向心加速度计算式a=ω2r正确性的方法.
-
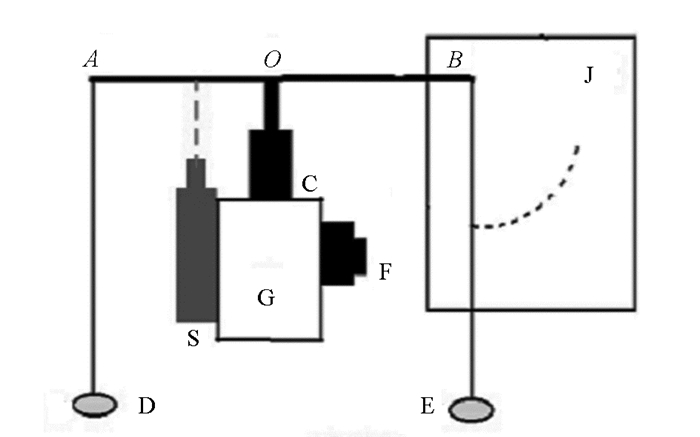
在杆右侧装上纸板J(图 6).向D和E中加入相同质量的水,并在实验过程中保持不变.调节调速器S旋钮到最低速度位置,闭合纸板J中电路.水平静止放置实验装置,并使两物体静止,这时右侧板背面的小灯泡发光.
根据前面的推导,只需验证gtan α=ω2r成立即可.假设物体以半径r1做匀速圆周运动时夹角为α1,将r1和α1代入g tanα=ω2r中可计算出对应的角速度ω1.将右侧细导线卡在该角度α1对应点上两根细针之间,打开电池盒开关和测速器,根据测速器上的示数缓慢调节物体角速度到ω1,此时导线成一直线不与细针接触,电路断开,小灯泡熄灭,说明在角速度ω1下,物体做匀速圆周运动时,细线与竖直方向的夹角为α1,因此实验现象便与理论推导相符,说明向心加速度计算式a=ω2r是成立的.
再取其他角度α2,α3,α4,…重复验证.
-
向心加速度计算式的定量验证实验现象与数据记录见表 1.由表 1可知,只有将物体做匀速圆周运动的角速度ω′调整到由向心加速度计算式
${\omega ^2} = \frac{{g\tan \alpha }}{{\frac{{AB}}{2} + l\sin \alpha }}$ 计算得出的角速度ω大小时,细软导线才会成一直线,灯泡熄灭.
3.1. 实验过程与方法
3.2. 实验结果与分析
-
本研究设计的装置取材方便,制作简单,不但可以定性演示向心加速度α与角速度ω、半径r的定性关系[1],还可定量验证向心加速度公式a=ω2r的正确性.实验原理不复杂,实验现象明显、形象直观,有助于学生对向心加速度计算公式的理解.



 下载:
下载: