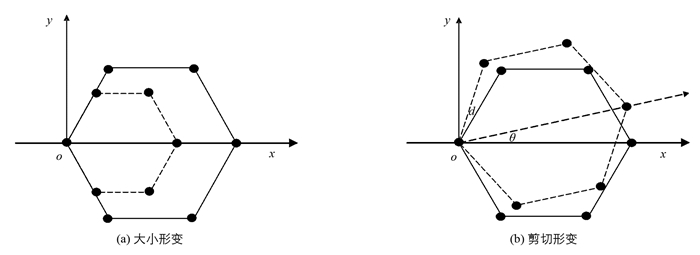
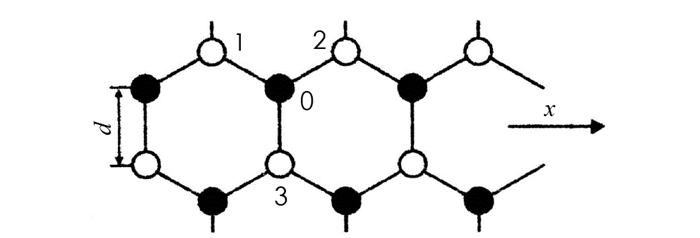
ZnS类石墨烯是由Zn原子和S原子构成的二维六角格子平面系统，设这两种原子各自总原子数为N，最近邻原子间距离为d(称键长)，取任一原子为坐标系原点，平面为OXY平面，φ(d)轴垂直向上，坐标系选取见图 1.

按文献[9]，考虑到短程作用后，ZnS类石墨烯的原子相互作用能为

其中，V₁为金属化能，$V_{2}=\eta \hbar^{2} / m d^{2}$是σ键的共价能，η=3.26；$V_{2}^{*}=\eta_{p p \pi} \hbar^{2} / m d^{2}$是π键的共价能，η_ppπ=0.63(文献[12])；V₃和V₃^*分别是σ键和π键的极化能，α_p和α_p^*分别是σ键和π键的极性参量，而α_c和α_c^*分别是σ键和π键的共价参量，其值为：

式中的常数C为短程作用参量，文献[10]给出C=0.20 eV.

为了克服文献[9]不能研究热力学性质随温度变化规律的不足，本文认为，在(1)式所示原子相互作用能的作用下，原子不是静止的，而是在平面内在平衡位置附近作非简谐振动.将φ(d)在平衡位置d₀附近展开，偏离δ=d-d₀很小时，有

其中，ε₀，ε₁，ε₂分别是简谐系数、第一和第二非简谐系数.由(1)式求得：

当温度不太高时，键长的平均位移ζ与温度的关系为^[11]

由(7)式求得在温度不太低和不太高时的热膨胀系数$\alpha_{l}=\frac{1}{d_{0}} \frac{d \xi}{d T}$为

弹性模量B随温度的变化为

其中，Ω为ZnS类石墨烯的原胞面积，它与最近邻原子间距离d₀的关系为$\Omega=(\sqrt{3} / 2) d_{0}^{2}$.

有效电荷，是指化合物中的实际电荷.当正、负离子组成化合物时，有效电荷与它们单独存在时的电荷不同.对ZnS类石墨烯，正、负离子有效电荷(以e为单位)分别为^[9]

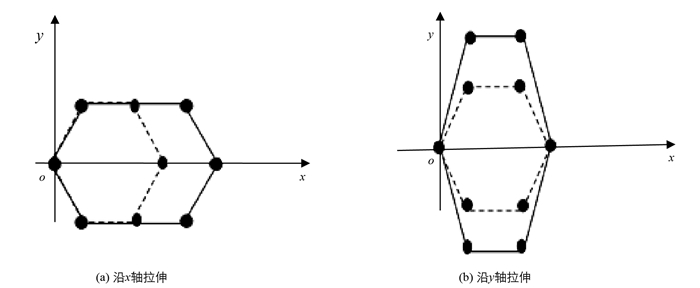
类石墨烯是二维材料，易发生形变，造成极性参量发生改变，进而引起有效电荷发生改变.它所发生的形变，包括两离子间距离变化的大小形变(图 2(a)、系统绕垂直平面的轴发生旋转的剪切形变(图 2(b))，还有单轴形变(图 3)等.

形变使其极性参量发生改变.大小形变使极性参量由α_p改变为α_p^′，α_p^*改变为α_p^′*.它们对d的相对变化量$\delta_{p}=d_{0}\left(\partial \alpha_{p} / \partial d\right)_{d_{0}}, \delta_{p}^{*}=d_{0}\left(\partial \alpha_{p}^{*} / \partial d_{0}\right)_{d_{0}}$称为键长形变极性变化率，剪切形变引起的对θ的变化τ_p=$\left(\partial^{2} \alpha_{p} / \partial \theta^{2}\right)_{\theta=0}, \tau_{p}^{*}=\left(\partial^{2} \alpha_{p}^{*} / \partial \theta^{2}\right)_{\theta=0}$称为剪切形变极性变化率.由α_p和V₂的表示式可求得：

这里的λ为表征剪切形变引起共价能V₂变化程度的参量，按文献[13]，取λ=0.66.

类石墨烯的极性改变，导致键长等的变化，进而导致ZnS有效电荷发生改变.

大小形变造成有效电荷Z₊，Z_-的改变随键长的变化率$\zeta_{\pm}=\left(\partial Z_{\pm} / \partial d\right)_{d_{0}}$经计算为：

剪切形变引起正负离子有效电荷改变量随转角θ的变化率$\eta_{\pm}=\left(\partial^{2} Z_{\pm} / \partial \theta^{2}\right)_{\theta=0}$经计算为：

单轴形变因改变离子电荷分布而产生有效电荷，其中，沿x轴的单轴形变产生的有效电荷为：

式中ζ为黎曼相对位移参量，由ζ=(1-λ)/(1+λ)求得.

沿y轴轴向形变产生新的有效原子电荷为：

由(13)-(16)式，可得几种形变造成的ZnS类石墨烯的正、负有效电荷(以e为单位)的改变量ΔZ₊，ΔZ_-为：

由(10)和(17)式，就得到ZnS类石墨烯形变后的有效电荷Z_±^′=Z_±+ΔZ_±.

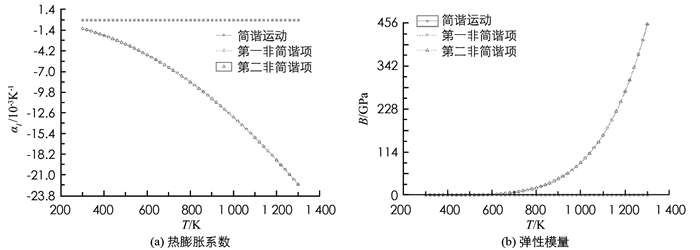
文献[8]给出ZnS类石墨烯有关数据为：d₀=2.19×10^-10m，V₁=2.80 eV，V₂=7.75 eV，V₂^*=1.52 eV，V₃^*=2.94 eV，由(2)式求得α_p=0.710，α_p^*=5.221，α_c=0.704，α_c^*=0.141.代入(4)、(5)、(6)式，求得：ε₀=3.97×10²J/m²，ε₁=-2.53×10¹²J/m³，ε₂=3.20×10²²J/m⁴.还可求得Ω=4.154×10^-20m³.将ε₀，ε₁，ε₂以及玻尔兹曼常数k_B代入(8)式和(9)式，得到ZnS类石墨烯热膨胀系数和弹性模量随温度的变化见表 1.表中的(0)，(1)，(2)分别是简谐近似、计算到第一非谐项、同时计算到第一、二非谐项的结果.变化曲线见图 4.

由表 1和图 4看出：①在所讨论的温度范围内，ZnS类石墨烯的热膨胀系数α_l为负值，且随温度升高而数值增大，其数值在1.178×10^-3-22.323×10^-3K^-1之间；②ZnS类石墨烯的弹性模量随温度升高而增大，其数值在0.241 405~453.253 5 GPa之间，其中，温度低于700 K时变化很小，而温度高于700 K后则迅速增大；③简谐近似下的热膨胀系数为零，弹性模量为常量.考虑非简谐项后，α_l和B均随温度升高而变化.温度愈高，非简谐效应愈显著；④第一非谐项和第二非谐项引起的α_l和B的差异极小.

将文献[14]以及前面计算的α_p等数据代入(11)、(12)式，求得：ZnS类石墨烯的大小形变和剪切形变引起的极性变化率δ_p，δ_p^*，τ_p分别为：δ_p=0.704，δ_p^*=0.039，τ_p=0.465.这表明：①大小形变引起键长形变极性变化率比剪切形变引起的极性变化率大，大小形变对其影响可达到70.4%，剪切形变对其影响仅为46.5%；②形变使ZnS类石墨烯的极性参量变大，而共价参量变小.

将上述数据代入(13)和(14)式，得到ZnS类石墨烯的3种形变对ZnS的几个有效电荷的影响参量(ζ₊，ζ_-，η₊，η_-)，结果是：对大小形变，ζ₊=2.820，ζ_-=-2.820；对剪切形变，η₊=1.395，η_-=-1.395.其余形变的ζ₊，ζ_-，η₊，η_-均为零.这表明：①单轴形变不会引起ZnS类石墨烯正负离子有效电荷的变化，而大小形变引起的变化比剪切形变引起的变化要大；②大小形变与剪切形变引起的正负离子有效电荷的变化相同.

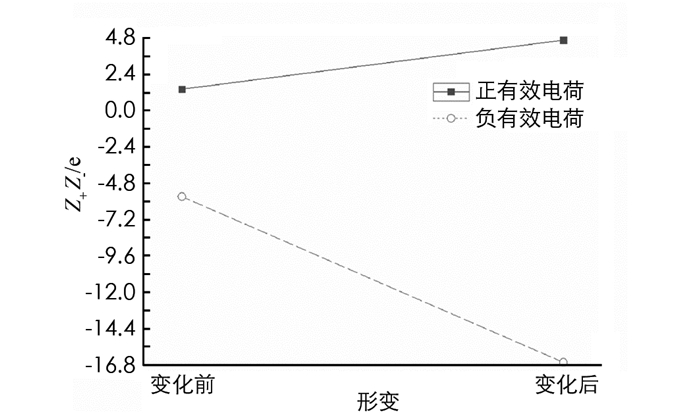
将上述数据代入(15)-(16)式，求得：ZnS类石墨烯的有效电荷形变前为：Z₊=1.417，Z_-=-5.676，而形变后为Z′₊=4.658，Z′_-=-16.621.其中大小形变、剪切形变、单轴形变对形变后有效电荷的贡献见表 2，而形变前后总有效电荷的变化见图 5.

由表 2和图 5看出：①形变使ZnS类石墨烯的正有效电荷由Z₊=1.417增大到Z′₊=4.658，负有效电荷由Z_-=-5.676变为Z′_-=-16.621，形变对负电荷的影响大于正电荷；②3种形变中，大小形变和单轴形变对正、负有效电荷的影响最大，剪切形变的影响最小.

1) 在所讨论的温度范围内，ZnS类石墨烯的热膨胀系数为负值，且随着温度的升高而数值增大，其数值在1.178×10^-3-22.323×10^-3K^-1之间.简谐近似下的热膨胀系数为零；考虑非简谐项后，热膨胀系数随温度升高而变化.温度愈高，简谐与非简谐的值的差愈大.非简谐项中，第二非简谐项的影响极小；

2) 弹性模量随温度升高而增大，数值在0.241 405~453.253 5 GPa之间.温度低于700 K时变化很小，而温度高于700 K后则迅速增大；简谐近似下为常数；考虑非简谐项后则随温度升高而增大.温度愈高，非简谐效应愈显著；温度较低时第二非谐项的影响才明显；

3) 单轴形变不会引起ZnS类石墨烯有效电荷的变化，而大小形变引起的变化大于剪切形变.形变对负电荷的影响大于正电荷；大小、剪切、单轴形变这3种形变中，大小形变对正有效电荷和单轴形变对负有效电荷影响最大，剪切形变的影响最小.

4) 大小形变对极性的影响可达到70.4%，剪切形变的影响仅为46.5%.