-
利率是我国经济宏观调控中的重要金融工具,也是近20年间市场化改革的一项重要工作[1].利率之所以能作为调控经济的有效工具,与其对货币流动的引导密切相关.通过利率调整,可以实现对金融流动性的释放或限制,从而有效调控经济过热或者经济过冷.从数学意义上讲,利率如何对宏观经济产生影响,需要通过利率期限结构加以建模进而展开分析[2].在利率期限结构模型中,又有静态模型和动态模型之分.静态利率期限结构模型首次出现是应用于企业债券的收益分析上,通过与收益曲线的拟合寻找利率对企业债券的影响.分段函数和样条函数也是静态利率期限结构的重要分析工具,通常可用作对现金折现率的分析[3-4].递归函数模型也应用于静态利率分析,可以计算票息分离的最佳理论点[5]. Nelson模型是静态利率分析中具有里程碑意义的一类模型,其优势在于模型形式简洁、拟合过程易于操作、拟合曲线光滑连续、预测效果准确[6].在静态利率分析的基础上,动态利率分析逐渐发展起来,并且更好地对应于利率与时间的变化关系.动态利率分析中最早出现的两个分析模型,分别是均衡模型和非套利模型[7-8].其后,卡尔曼滤波因其对动态数据的良好过滤效果,也被引入到动态利率分析之中[9].类似的还有蒙特卡洛分析模型和在Nelson模型基础上改进而来的Svensson模型(斯文森模型),斯文森模型因其分析过程的完整性成为利率分析的有效工具[10-11].建立利率期限结构模型之后,其中的很多特征可以用于分析利率与宏观经济的关系,如长期利率参数、短期利率参数、长短利差参数、名义利率参数、实际利率参数等等.这些参数与宏观经济表征参数之间的关系可以通过相关分析、回归分析、VAR(Value at Risk)脉冲分析、协整分析、格兰杰因果分析等手段实现[12].在本文的研究工作中,将首先借助斯文森分析构建利率期限结构模型,进而以其中的关键参数为表征变量,分析其与宏观经济之间的关系.
全文HTML
-
Nelson模型是利率分析领域的里程碑式研究成果,而斯文森模型也是建立在Nelson模型基础之上的.故此,先来阐述Nelson模型.
Nelson模型的数学描述为
函数fI(τ)表示期限在τ年中一共获得的零息债券收益;参数β0表示利率的长期变化,称作长期参数;参数β1表示利率的短期变化,称作短期参数;参数β2表示利率的中期变化,称作中期参数;参数λ表示的是一个时间常数.
经过进一步研究发现:参数β1影响到函数fI(τ)的曲线倾斜方向,因此也被称为倾斜因子,在很多情况下,参数β1也表示长短利率之间的差值;参数β2则控制着函数fI(τ)的曲线弯曲弧度,因此也被称为曲度因子.
如果要计算长期利率在某个时间点上的即期利率,可以采用如下的积分形势来分析长期利率和即期利率的关系.
进而可以计算出即期利率的大小,结果为
Nelson模型涵盖了利率的多种特征,并且模型结构简洁、操作灵活、曲线拟合效果好.但是对于利率期限结构较为复杂的情况显得力不从心.针对Nelson模型的不足,斯文森模型被建立出来,这是一个比Nelson模型复杂一些、但使用范围更广的一类利率分析模型,其基本形式为
同Nelson模型相比,斯文森模型多出了一个参数β3,复杂性更高些,但解决实际问题的能力也得到增强,可以拟和更为复杂的利率期限结构.
根据斯文森模型,要计算即期利率,可以采用如下的公式
-
为了便于分析宏观经济和利率之间的关系,本文选取了4个变量,协同参与接下来的实证研究工作.这4个实证变量分别是:国民生产总值GDP,用于经济发展速度;消费价格指数CPI,用于反映经济发展周期中的物价涨跌情况;广义货币发行量M2,用于反映经济发展过程中的货币发型总量;一年定期存款利率I,用于反映经济发展周期中的利率变化情况.
在这4个变量中,GDP反映我国经济总量的增长情况,CPI反映我国经济中的通货膨胀率,M2反映我国经济中的广义货币发行量,这3个变量都是宏观经济指标的代表;I则是利率的代表.
依据这4个变量,在中国统计年鉴中选取2000-2017年的相关数据,结果如表 1所示.
-
实证研究的第一步工作,是确定斯文森利率模型中的4个关键参数,将表 1中的利率数据代入公式(4)进行迭代,确定出的4个关键参数如表 2所示.
-
经过ADF(Augmented Dickey-Fuller)检验和协整检验,证明GDP,CPI,M2,β0,β1,β2,β3满足同阶单整并存在一个长期均衡关系.
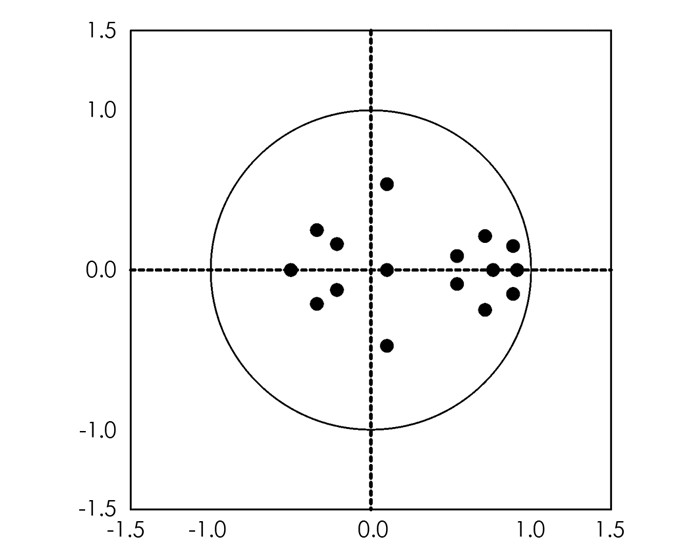
接下来执行单位圆检验,在ADF后的单位圆检验主要用于考察分析过程的整体稳定性.如果单位圆检验结果,全部特征根的倒数都位于单位圆中,那么就表明整个分析过程稳定,可以进行后续的分析.如果单位圆检验结果,不是全部特征根的倒数都位于单位圆中,那么就表明整个分析过程不稳定,需要修改前述的参数配置和模型构建,直到全部特征根的倒数都位于单位圆中,才能进行后续的分析.
本文ADF分析后,执行单位圆检验,全部特征根的倒数分布情况如图 1所示.
从图 1的结果中可以看出,各变量特征根的倒数都位于单位圆内,故整个分析模型稳定,可以继续进行后续的分析.
根据ADF,进一步执行单位根检验,结果如表 3所示.
从表 3的结果可以看出,GDP,CPI,M2,I这4个变量的检验值都大于3个检验水平的评估值,这表明GDP,CPI,M2,I这4个变量是同阶稳定的,可以进行进一步的格兰杰检验.
在ADF、单位圆检验之后,再执行进一步的格兰杰因果分析,结果如表 4所示.
从表 3中的结果可以看出,对于斯文森利率模型中的关键参数β0与宏观经济变量GDP,CPI,M2之间的格兰杰因果关系假设,假设“B0不是M2的格兰杰原因”被拒绝(F:4.778 3,p:0.025 8,显著水平在5%以下).参数β0反映的是长期利率水平,这一结果表明长期利率是广义货币量M2增加的格兰杰原因.
对于斯文森利率模型中的关键参数β1与宏观经济变量GDP,CPI,M2之间的格兰杰因果关系假设,假设“GDP不是B1的格兰杰原因”被拒绝(F:5.521 6,p:0.019 7,显著水平在5%以下),假设“M2不是B1的格兰杰原因”被拒绝(F:4.875 6,p:0.027 8,显著水平在5%以下).参数β1反映的是短期利率水平,这一结果表明国民生产总值GDP和广义货币量M2都是短期利率变化的格兰杰原因.
对于斯文森利率模型中的关键参数β2与宏观经济变量GDP,CPI,M2之间的格兰杰因果关系假设,假设“GDP不是B2的格兰杰原因”被拒绝(F:5.512 8,p:0.022 2,显著水平在5%以下),假设“M2不是B2的格兰杰原因”被拒绝(F:5.010 1,p:0.032 8,显著水平在5%以下).参数β2反映的是中期利率水平,这一结果表明国民生产总值GDP和广义货币量M2都是中期利率变化的格兰杰原因.
除了上述5项检验结果确定了5种格兰杰因果关系以外,其余的假设都被验证,包括分析变量GDP不是分析变量B0的格兰杰原因,分析变量B0不是分析变量GDP的格兰杰原因,分析变量CPI不是分析变量B0的格兰杰原因,分析变量B0不是分析变量CPI的格兰杰原因,分析变量M2不是分析变量B0的格兰杰原因,分析变量B1不是分析变量GDP的格兰杰原因,分析变量CPI不是分析变量B1的格兰杰原因,分析变量B1不是分析变量CPI的格兰杰原因,分析变量B1不是分析变量M2的格兰杰原因,分析变量B2不是分析变量GDP的格兰杰原因,分析变量CPI不是分析变量B2的格兰杰原因,分析变量B2不是分析变量CPI的格兰杰原因,分析变量B2不是分析变量M2的格兰杰原因.
2.1. 实证变量及数据选取
2.2. 斯文森利率模型参数的确定
2.3. 宏观经济各变量与斯文森利率模型中关键参数的关系研究
-
为了分析宏观经济和利率之间的关系,在Nelson模型的基础上阐述了斯文森利率模型的改进策略和效果,明确了其中的关键参数及其代表的利率意义.选取国民生产总值GDP、消费价格指数CPI、广义货币量M2作为宏观经济的表征变量,选取一年定期存款利率I作为利率的表征变量,构建了斯文森模型,选取2000-2017年间的相关数据展开实证研究.
实证研究过程中,在斯文森模型下使用了ADF检验、特征根的单位圆检验、格兰杰因果检验.国民生产总值GDP、消费价格指数CPI、广义货币量M2、一年定期存款利率I这4个变量所构建的模型,都通过了ADF检验和特征根的单位圆检验.
进一步的格兰杰因果检验显示:
1) 在斯文森模型下,“B0不是M2的格兰杰原因”被拒绝,表明长期利率是广义货币量M2增加的格兰杰原因.
2) 在斯文森模型下,“GDP不是B1的格兰杰原因”被拒绝,表明国民生产总值GDP是短期利率变化的格兰杰原因.
3) 在斯文森模型下,“M2不是B1的格兰杰原因”被拒绝,表明广义货币量M2是短期利率变化的格兰杰原因.
4) 在斯文森模型下,“GDP不是B2的格兰杰原因”被拒绝,表明国民生产总值GDP是中期利率变化的格兰杰原因.
5) 在斯文森模型下,“M2不是B2的格兰杰原因”被拒绝,表明广义货币量M2是中期利率变化的格兰杰原因.
根据上述结论,本文给出如下对策建议:
1) 在斯文森模型的分析之下,广义货币量M2和利率之间有着比较明显的联系.因此从宏观经济角度考虑,为了确保广义货币量发行稳定,应该进行合理的利率配置,无论是短期利率、中期利率、长期利率,都应该是在科学核算的基础上制定结果,并应充分地对经济形势有比较清晰的预判,根据经济发展趋势制定利率预案.
2) 宏观经济最有代表性的GDP指标对中期利率和短期利率都有明确的影响,这也就要求利率制定必须充分地分析GDP总量、GDP变化趋势,才能充分遵循GDP和利率之间相互关联的客观规律,真正地实现利率作为有效金融工具的价值.



 下载:
下载: