-
自1834年苏格兰工程师Russell发现一种称之为孤立波的非线性波以来,人们对于非线性波的研究就进入了一个新的时代.随着科学技术的发展和研究的深入,科研人员发现波形在传播中是陡峭还是光滑与所研究的问题中是否存在色散现象和非线性现象有着直接的联系.例如:在著名的Korteweg-de Vries(KdV)方程
中,对流项uux(非线性项)和线性色散项uxxx就决定了孤立波的形状及其陡峭和光滑程度.显然,这两项的相互作用产生了完全光滑的孤波解[1].
为了研究非线性色散在液滴图案形成中的作用,文献[2]研究了K(2,2)方程
中的非线性色散与非线性对流的相互作用.研究表明:非线性色散与非线性对流的相互作用可以使孤波紧化,也就是说具有紧化的孤立波没有无限翼,这类非线性波称之为紧波(compacton wave).类似地,文献[3-4]在最近的报告中采用动力系统面分支法研究了广义的K(2,2)方程
的各种行波解,其中负色散项表示收缩色散,获得了方程(1)更多类型的行波解,这些解的形状有孤立尖波峰波、周期尖峰波和平滑波等.这些解被看作非线性收缩色散与非线性对流之间相互作用而产生的结果.关于Camassa-Holm方程其它方向的研究可以参看文献[5-7],而关于K(2,2)方程的更多研究见文献[8-10]及其引用文献.
值得一提的是著名的Camassa-Holm(CH)方程[11]
与我们要研究的K(2,2)方程有类似的结构,且CH方程与方程(1)均含有相同的非线性项,但区别还是比较大.许多研究者利用不同的方法给出了CH方程的各种行波解[12-15],却发现它们大多不是光滑解,为了解释这些奇怪的现象,文献[16]作了深入研究,获得了许多新成果,为非线性波的研究做出了较大的贡献.文献[16]还给出了弱解的定义,最终获得了CH方程极为丰富的行波解,包括峰波解、孤立尖波解和紧波解等.然而,对一些有趣的解,如环状形式的解、扭结形式的解和其它形式的解及其动力学现象并没有相关研究.此外,对解的极限行为也没有进一步研究.
为此,本文针对以上问题,结合上述研究方法中的一些优点,在改进方法的基础上,进一步研究方程(1)在各参数条件下的行波解及其动力学现象.
全文HTML
-
通过使用行波变换,可将偏微分方程(1)化简为一个可积ODE,并通过二维平面导出其积分方程.作一个行波变换
将(2)式代入方程(1)得到
其中c是沿x轴方向运动的波速.对(3)式积分,可以得到
其中g是积分常数.令
${\varphi _\xi }{\rm{ = }}\frac{{{\rm{d}}\varphi }}{{{\rm{d}}\xi }} = y$ ,当φ≠0时,(4)式能被简化为一个二维系统但是当φ=0时,系统(5)并不等于(4)式.为了得到一个完全等价的系统,不管(4)式函数φ如何变化,作变量替换
此处τ是参数.在变换(6)下,系统(5)化为常规系统
显然,系统(5)和系统(7)具有相同的首次积分
其中h是另一个积分常数. (8)式能被写成
从(7)式和(9)式,我们很容易验证
$\frac{{{\rm{d}}\varphi }}{{{\rm{d}}\tau }} \ne - \frac{{\partial H}}{{\partial y}}$ ,$\frac{{{\rm{d}}y}}{{{\rm{d}}\tau }} \ne \frac{{\partial H}}{{\partial \varphi }}$ .因此,系统(7)不是哈密顿系统.在H(φ,y)=h(h为常数)的条件下,虽然全局能源是受能源保护的,但是系统的动能和势能并不守恒,这意味着方程(1)包含许多行波解.
-
下面将研究积分常数h,g在h=g=0,h=0;g≠0,h≠0;g=0,h≠0;g≠0这4种情形下方程(1)的精确行波解,并讨论其动态特性.
-
此时,(8)式可以被化简为
当a>0时,将(10)式代入系统(5)的第一个方程,有
对(11)式积分,得到
其中c是常数.因此,将(12)式代入u(x,t)=φ(ξ),得到关于方程(1)的一个精确行波解
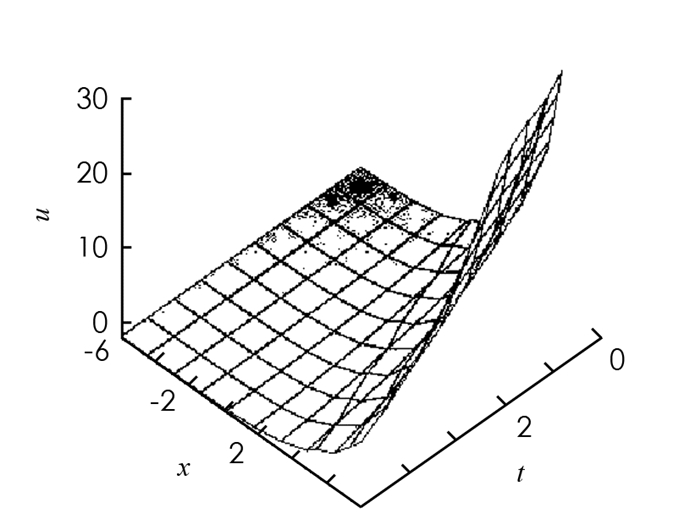
在(13)式中,取a=1,c=1,c1=1,得u(x,t)的图形如图 1所示.
当a < 0时,将(10)式代入系统(5)的第一个方程并进行积分,可以得到
其中c1是常数.于是,将(14)式代入u(x,t)=φ(ξ),便获得方程(1)的精确行波解
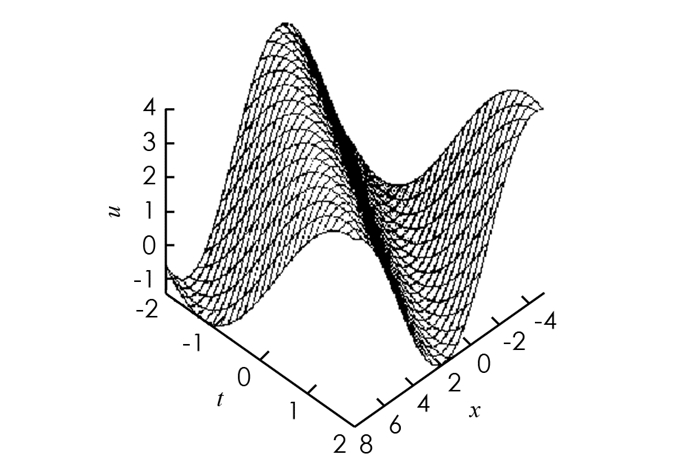
在(15)式中,取a=-1,c=1,c1=1,此时u(x,t)的图形如图 2所示.
特别地,当
${c_1} = - \frac{c}{3}$ 时,(12)式能被化简为因此,将(16)式代入u(x,t)=φ(ξ),可以获得方程(1)的精确行波解
-
此时,(8)式可以简化为
将(18)式代入系统(5)的第一个方程,可以得到
当a>0时,对(19)式积分,可以得到
因此,将(20)式积分,代入u(x,t)=φ(ξ),可以获得方程(1)的精确行波解
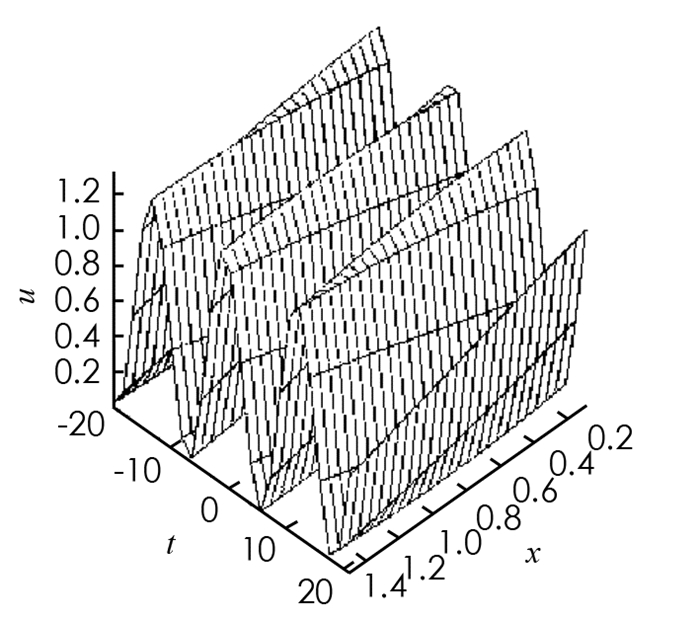
在(15)式中,取a=1,c=2,c1=1,g=3,此时u(x,t)的图形如图 3所示.
-
此时,(8)式可以简化为
将(22)式代入系统(5)的第一个方程,可以得到
也就是
当a < 0时,令
$\varphi = \psi + \frac{c}{{3a}}$ ,$h = - \frac{{{c^4}}}{{108{a^3}}}$ ,于是,(24)式可化简为其中
$p = - \frac{{2{c^2}}}{{3{a^2}}}, \varphi = \psi + \frac{c}{{3a}}, q = - {\left( {\frac{{2c}}{{3a}}} \right)^3}$ .记
$\Delta = {\left( {\frac{q}{2}} \right)^2} + {\left( {\frac{p}{3}} \right)^3}$ ,易知$\Delta = \frac{{8{c^6}}}{{729{a^6}}} > 0$ ,且方程ψ3+pψ+q=0有3个不同的根,分别是:于是,(25)式可以重新写为
对(26)式积分,可得
其中c1是任意常数,并且
-
此时,(8)式可以简化为
将(28)式代入系统(5)的第一个方程,可以得到
即
令
$\varphi = \psi + \frac{c}{{3a}}$ ,于是(30)式被化简为其中
$p = - \frac{{2{c^2} + 6ag}}{{3{a^2}}}, q = - \frac{{8a{c^3} + 36gc{a^2}}}{{27{a^4}}}, r = - \frac{{{c^4} + 6ga{c^2} + 108h{a^3}}}{{27{a^4}}}$ .当q=0,即$g = - \frac{{2{c^2}}}{{9a}}$ 时,有$p = - \frac{{2{c^2}}}{{9{a^2}}}, r = \frac{{{c^4} - 324h{a^3}}}{{81{a^4}}}$ ,因此(31)式变为即
由(33)式可以获得
其中c1是任意常数,并且
当q≠0时,(31)式被化简为
其中ψ1>ψ2>ψ3>ψ4,且满足
其中k0是(36)式的任一根.解(35)式,可得
其中c1是任意常数,并且
2.1. h=g=0时方程(1)的精确解
2.2. h=0,g≠0时方程(1)的精确解
2.3. h≠0,g=0时方程(1)的精确解
2.4. h≠0,g≠0时方程(1)的精确解
-
本文首先利用行波变换进行约简,将方程(1)转化为可积ODE,并通过二维平面动力学推导出其第一个积分方程系统,然后采用积分法研究了不同类型的精确行波解,最后讨论了它们的动力学性质.



 下载:
下载: