高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

太阳能干燥箱的自然对流数值模拟与实验研究

,  ,  , 

上一篇

下一篇

张凯, 胡众欢, 杨明金, 等. 太阳能干燥箱的自然对流数值模拟与实验研究[J]. 西南师范大学学报(自然科学版), 2020, 45(12): 58-64. doi: 10.13718/j.cnki.xsxb.2020.12.010
引用本文: 张凯, 胡众欢, 杨明金, 等. 太阳能干燥箱的自然对流数值模拟与实验研究[J]. 西南师范大学学报(自然科学版), 2020, 45(12): 58-64. doi: 10.13718/j.cnki.xsxb.2020.12.010
shu
ZHANG Kai, HU Zhong-huan, YANG Ming-jin, et al. Numerical Simulation and Experimental Study of Natural Convection in Solar Drying Box[J]. Journal of Southwest China Normal University(Natural Science Edition), 2020, 45(12): 58-64. doi: 10.13718/j.cnki.xsxb.2020.12.010
Citation: ZHANG Kai, HU Zhong-huan, YANG Ming-jin, et al. Numerical Simulation and Experimental Study of Natural Convection in Solar Drying Box[J]. Journal of Southwest China Normal University(Natural Science Edition), 2020, 45(12): 58-64. doi: 10.13718/j.cnki.xsxb.2020.12.010
shu

太阳能干燥箱的自然对流数值模拟与实验研究

  • 西南大学 工程技术学院/丘陵山区农业装备重庆市重点实验室，重庆 400716

  • 基金项目: 国家自然科学基金(31301575)
详细信息
    作者简介:

    张凯(1996-)，男，硕士研究生，主要从事太阳能干燥传热机理及模型研究 .

    通讯作者: 杨玲，女，教授，硕士生导师

  • 中图分类号: S226.6

Numerical Simulation and Experimental Study of Natural Convection in Solar Drying Box

  • College of Engineering and Technology/Chongqing Key Laboratory of Agricultural Equipment for Hilly and Mountainous Regions, Southwest University, Chongqing 400716, China

  • 摘要: 为了得到自然对流传热状态下太阳能干燥箱流热场具体分布情况，针对一种小型太阳能干燥箱的自然对流传热过程建立了数学模型，并通过COMSOL Multiphysics多物理场软件对数学模型进行求解.详细分析了集热板与空气之间的自然对流换热过程，并由干燥室内温度模拟值与实验值构建均匀度曲线与温度变化曲线，得到干燥室内温度分布随时间的变化情况.计算出不同的天气下(多云、晴朗、少云)温度模拟值与实验值的相关系数R2分别为0.967，0.978，0.956，均方根误差RMSE分别为2.289，1.821，1.940，说明所构建的数学模型在不同天气情况下的求解结果是有效的，根据流热场的模拟结果可以指导干燥工艺的优化和改进太阳能烘干系统的结构.
    Abstract: In order to obtain distribution of flow heat field of solar drying box under condition of natural convection heat transfer, a mathematical model of natural convection heat transfer process of a small solar drying box was established in this paper. The mathematical model was solved by COMSOL Multiphysics, and the natural convection heat transfer process between heat collecting plate and air was analyzed in details. The curves of heat uniformity and temperature change were plotted from simulated and experimental temperature in the drying box. The change of temperature distribution in the drying box over time was obtained. The correlation coefficients R2 of simulated temperature and experimental values under different weather conditions (cloudy, sunny and partly cloudy) were 0.967, 0.978, and 0.956, with root mean square errors RMSE 2.289, 1.841, and 1.940, respectively, which indicated that the presented mathematical model was valid on different weather conditions. Therefore, based on simulation of the flow heat field, guidance can be provided for optimization of the drying process and improvement of the solar drying system structure.
  • 加载中

  • 图 1  干燥箱三维模型与结构简图

    下载: 全尺寸图片 幻灯片

    图 2  二维模型(单位：mm)

    下载: 全尺寸图片 幻灯片

    图 3  Ra与Th分段函数图

    下载: 全尺寸图片 幻灯片

    图 4  混合型网格

    下载: 全尺寸图片 幻灯片

    图 5  相对标准偏差CV与温度T随时间变化情况

    下载: 全尺寸图片 幻灯片

    图 6  温度云图(6月2日)

    下载: 全尺寸图片 幻灯片

    图 7  速度云图(6月2日240 min)

    下载: 全尺寸图片 幻灯片

    表 1  R2与RMSE计算结果

    5月17日 6月2日 7月1日
    R2 0.967 0.978 0.956
    RMSE 2.289 1.821 1.940
    下载: 导出CSV
  • [1] 郝文刚, 陆一锋, 赖艳华, 等.开放式太阳能物料干燥热湿迁移模型的构建及验证[J].农业工程学报, 2017, 33(15): 301-307. doi: http://www.cnki.com.cn/Article/CJFDTotal-NYGU201715038.htm
    [2] 柳丽萍, 钱文春, 占鹏飞, 等.不同基质和干燥方法对大球盖菇营养成分的影响[J].西南大学学报(自然科学版), 2018, 40(2): 8-13. doi: http://d.wanfangdata.com.cn/periodical/xnnydxxb201802002
    [3] SINGH P, SHRIVASTAVA V, KUMAR A. Recent Developments in Greenhouse Solar Drying: A Review[J]. Renewable and Sustainable Energy Reviews, 2018, 82: 3250-3262. doi: 10.1016/j.rser.2017.10.020
    [4] FUDHOLI A, SOPIAN K, BAKHTYAR B, et al. Review of Solar Drying Systems With Air Based Solar Collectors in Malaysia[J]. Renewable and Sustainable Energy Reviews, 2015, 51: 1191-1204. doi: 10.1016/j.rser.2015.07.026
    [5] GBAHA P, ANDOH H Y, SARAKA J K, et al. Experimental Investigation of a Solar Dryer With Natural Convective Heat flow[J]. Renewable Energy, 2007, 32(11): 1817-1829. doi: 10.1016/j.renene.2006.10.011
    [6] TIWARI S, TIWARI G N, Al-Helal I M. Performance Analysis of Photovoltaic-Thermal (PVT) Mixed Mode Greenhouse Solar Dryer[J]. Solar Energy, 2016, 133: 421-428. doi: 10.1016/j.solener.2016.04.033
    [7] 郝文刚, 陆一锋, 赖艳华, 等.直接式太阳能干燥系统的热性能分析及应用[J].农业工程学报, 2018, 34(10): 187-193. doi: http://www.cqvip.com/main/zcps.aspx?c=1&id=675283927
    [8] 任海伟, 李金平, 刘增光, 等.太阳能干燥室内部气流场分布CFD数值模拟[J].农业机械学报, 2012, 43(S1): 235-238. doi: http://d.wanfangdata.com.cn/Periodical/nyjxxb2012z1048
    [9] SINGH A P, SINGH O P. Performance Enhancement of a Curved Solar Air Heater Using CFD[J]. Solar Energy, 2018, 174: 556-569. doi: 10.1016/j.solener.2018.09.053
    [10] GUPTA D, SOLANKI S C, SAINI J S. Heat and Fluid Flow in Rectangular Solar Air Heater Ducts Having Transverse Rib Roughness on Absorber Plates[J]. Solar Energy, 1993, 51(1): 31-37. doi: 10.1016/0038-092X(93)90039-Q
    [11] 王国安, 米鸿涛, 邓天宏, 等.太阳高度角和日出日落时刻太阳方位角一年变化范围的计算[J].气象与环境科学, 2007, 30(S1): 161-164. doi: http://d.wanfangdata.com.cn/Periodical/hnqx2007z1050
    [12] 戴锅生.传热学[M]. 2版.北京:高等教育出版社, 1999.
    [13] SARTON G. On The Theories of The Internal Friction of Fluids in Motion[J]. Trans camb philos soc, 2004, 8(2): 153-169.
    [14] 颜菲尔, 李伟清.尖顶型温室风压数值模拟与研究[J].西南师范大学学报(自然科学版), 2017, 42(2): 127-132. doi: http://xbgjxt.swu.edu.cn/article/doi/10.13718/j.cnki.xsxb.2017.02.022
    [15] 苏杭, 张永东, 刘希臣, 等.某酒店中庭冬季空调气流组织数值模拟与实测研究[J].西南师范大学学报(自然科学版), 2015, 40(4): 78-82. doi: http://xbgjxt.swu.edu.cn/article/doi/10.13718/j.cnki.xsxb.2015.04.016
    [16] INCROPERA F P, DEWITT D P, BERGMAN T L, et al. Fundamentals of Heat and Mass Transfer[M], 6th ed., Manhattan: John Wiley & Sons, 2006.
    [17] PRYOR R W. Multiphysics Modeling Using COMSOL: A First Principles Approach[M]. London: Jones and Bartlett Publishers, 2011.
    [18] 李坦, 靳世平, 黄素逸, 等.流场速度分布均匀性评价指标比较与应用研究[J].热力发电, 2013, 42(11): 60-63. doi: http://www.cnki.com.cn/Article/CJFDTotal-RLFD201311013.htm
    [19] HAMDI I, KOOLI S, ELKHADRAOUI A, et al. Experimental Study and Numerical Modeling for Drying Grapes Under Solar Greenhouse[J]. Renewable Energy, 2018, 127: 936-946. doi: 10.1016/j.renene.2018.05.027
  • 加载中
图( 7) 表( 1)
计量
  • 文章访问数:  1474
  • HTML全文浏览数:  1474
  • PDF下载数:  153
  • 施引文献:  0
出版历程
  • 收稿日期:  2019-08-05
  • 刊出日期:  2020-12-20

太阳能干燥箱的自然对流数值模拟与实验研究

    通讯作者: 杨玲，女，教授，硕士生导师
    作者简介: 张凯(1996-)，男，硕士研究生，主要从事太阳能干燥传热机理及模型研究
  • 西南大学 工程技术学院/丘陵山区农业装备重庆市重点实验室，重庆 400716
  • 收稿日期:  2019-08-05
基金项目:  国家自然科学基金(31301575)

摘要: 为了得到自然对流传热状态下太阳能干燥箱流热场具体分布情况，针对一种小型太阳能干燥箱的自然对流传热过程建立了数学模型，并通过COMSOL Multiphysics多物理场软件对数学模型进行求解.详细分析了集热板与空气之间的自然对流换热过程，并由干燥室内温度模拟值与实验值构建均匀度曲线与温度变化曲线，得到干燥室内温度分布随时间的变化情况.计算出不同的天气下(多云、晴朗、少云)温度模拟值与实验值的相关系数R2分别为0.967，0.978，0.956，均方根误差RMSE分别为2.289，1.821，1.940，说明所构建的数学模型在不同天气情况下的求解结果是有效的，根据流热场的模拟结果可以指导干燥工艺的优化和改进太阳能烘干系统的结构.

English Abstract

    全文HTML

  • 太阳能具有清洁、可再生的特点，在干燥领域有良好的应用前景.直接晾晒法是一种极具代表性的太阳能干燥方法[1]，从古至今一直被广泛应用于农作物干燥，但是直接晾晒法有劳动强度大、无法控制干燥条件、对天气因素依赖大、效率低、干燥品质差等缺陷[2].大量学者对太阳能干燥进行了一系列的研究，开发出了各种各样的太阳能干燥设备，弥补了直接晾晒法的各种不足，其中较具代表性的设备有储能热泵式与混合能源式两类[3-4]，这两类设备多数呈现出大型化、专业化与高成本的特征，并不适宜于小型农户使用.在我国小型农户占据着农业经济的较大比重，因此有必要对小型化、简单化、低成本的太阳能干燥设备进行研究.在对太阳能干燥设备的研究与优化中，研究者通常希望获取干燥室内流场、热场的分布情况，实验手段获取物理场数据难度大、成本高、可重复性差[5]，因此众多学者将数值模拟技术应用于太阳能干燥的研究，并以此来弥补实验手段的不足.在对干燥设备的流热数值模拟研究中，部分研究[6-7]基于干燥箱内部流热场稳定均匀的假设，忽略了干燥箱内空间上的流热场差异.而在考虑了箱内的流热场具体分布情况的研究[8-10]中，多数是对干燥箱强制对流换热过程的具体数值模拟.由于自然对流过程难以达到稳态，且计算量大，目前对于干燥箱自然对流传热的数值模拟研究较少.

    综上所述，本文结合传热学与计算流体力学，在自制小型太阳能干燥箱的基础上，建立了干燥箱自然对流状态的流热数学模型，利用COMSOL Multiphysics 5.4软件求解干燥箱数学模型，尝试在不同的天气条件下，通过数学模型得到较为准确的干燥箱内自然对流的具体情况，为干燥工艺方案和改进干燥箱的结构优化方案提供理论基础.

1.   干燥箱结构及实验设计

    1.1.   干燥箱结构

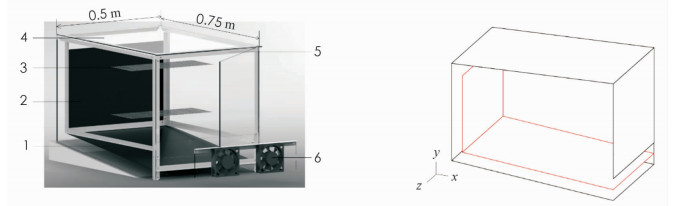
  • 该干燥箱主要由有机玻璃板、铝合金框架、主集热板、侧集热板和物料托盘(可加装多层)组成.在干燥要求低温干燥的物料时，可加装图 1所示的排湿风扇强制通风.本文只针对自然对流的情况展开讨论.由图 1可以看出装置在z方向上结构对称.根据公式(1)得到太阳高度角[11]：

    式中α为太阳高度角；φ为地理纬度；δ为太阳赤纬.实验地点在重庆北碚，地理纬度取29.8°N，太阳赤纬取23°，经计算太阳高度角为83.2°.为方便制造与计算，主集热板最佳倾角取6.8°(与太阳高度角互为余角)，侧集热板竖直安装在铝合金框架上.

    • 1.2.   实验材料与方法

  • 实验设备：TBQ-2型总辐射表(锦州阳光科技有限公司，误差±2%)用于测量实验过程中的太阳辐射值；妙昕TH20R-EX温湿度记录仪(平阳县妙观科技有限公司，温度误差±0.3 ℃，湿度误差±3%rh)用于测量实验过程中各点的温度值；水银温度计(量程0~100 ℃，精度1 ℃)用于测量环境温度；太阳能干燥箱(自制).

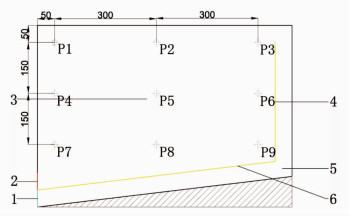
    实验方法：本次实验分为三组空晒实验，分别选取不同时间不同天气情况.第一组实验时间为2019年5月17日9：00-17：00，多云.第二组实验时间为2019年6月2日9：00-17：00，天气晴朗，无云.第三组实验时间为2019年7月1日9：00-17：00，少云.通过记录仪器测取太阳辐照度与干燥箱内温度的实时变化情况，干燥箱内的温度采样点为P1-P9，其分布情况如图 2所示.外界环境温度变化较慢，每隔15 min记录一次.

2.   数学模型

    2.1.   假设条件

  • 为减少计算量，在保证计算结果精确的前提下对模型进行简化.

    1) 自制太阳能干燥设备所采用的材料有比热小、质量轻等特点，可忽略设备自身所吸收的热量.

    2) 由于实验进行都处于无风或微风情况下，可以忽略外界风速对出入口以及边界热通量的影响.

    3) 干燥装置在z方向结构对称，为了减少计算量只进行二维模拟即可.

    • 2.2.   控制方程

  • 二维模型如图 2所示，P1-P9为数值模拟与实验的数据采样点.

    该模型可看做有限空间的自然对流，对格拉晓夫数进行估算[12](格拉晓夫数约为1011，大于109)，判断室内的流体状态为湍流，又因为自然对流情况下空气流速较低，选用低雷诺数k-ε模型来模拟流场，流热场求解基于三大控制方程，即能量守恒方程(2)，动量守恒方程(5)和连续性方程(7)：

    空气的基础物性参数(ρ，Cp，kc，u)来自COMSOL内置材料库.其中ρ为空气密度(kg/m2)；Cp为空气比热容(J/(kg·K))，其值为温度T的函数；T为温度(K)；t为时间(s)；u为速度(m/s)；Q为热源；q0为边界热通量；Qp为压力变化所做的功，其值由公式(4)可得；Qvd为粘性耗散[13]；q为热通量；kc为空气导热系数(W/(m·K))，其值为温度T的函数.

    其中αp为空气热膨胀系数(1/K)，对于理想气体来说其值为1/T；p为压力(Pa).

    其中F为体积力，值为0；g为重力加速度，值为-9.806 7(m/s2)；μ为运动粘度，其值为温度T的函数(Pa·s)；μT为涡流粘度(Pa·s).

    k为湍流动能(m2/s2)，ε为湍流耗散量(m2/s3)；Cμ为模型常数，值为0.09.由于流体假设为不可压缩流体，故连续性方程为[14]

    • 2.3.   物理场与边界条件

  • 添加非等温流动多物理场来进行湍流物理场和流体传热物理场的多场耦合，在不可压缩流体中，浮力项ρg带来的影响根据Boussinesq近似进行计算[15].

    由于太阳光理论上被认为是无穷远处发出的平行光，所以忽略侧集热板和主集热板之间的高度差.将侧集热板投影到主集热板所在的平面，可计算出侧集热板受太阳直射的有效面积为侧集热板面积与sin6.8°的乘积.将直射面积的影响换算到侧集热板的热源输入中，同时考虑集热板的辐射散热造成的热量流失，侧集热板的热源输入可表示为

    主集热板的热源输入为

    其中Ra为太阳辐照度(W/m2)；β为有机玻璃板的透射率，分别通过实验测得在有机玻璃板覆盖情况下实验仪器的辐照度与无覆盖情况的辐照度，通过二者的比值可求得β=0.9；γ为集热板对太阳光的表面吸收率，其值为0.8；Qre为辐射散热量(W/m2).由于周围环境面积远远大于集热板面积，故集热板的辐射散热量可表示为[12]：

    Th为环境温度(K)；σ为斯特藩-玻尔兹曼(Stefan-Boltzmann)常量，其值为5.67×10-8W/(m2·K4).

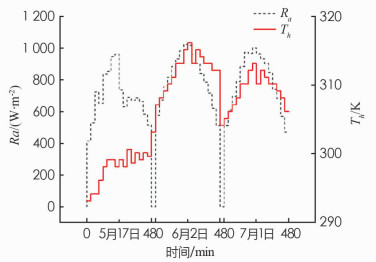
    为了减少数值模拟的计算量，将9：00-17：00之间实验每30 min测得的辐照度和环境温度数据取平均值，作为对应时间段模拟的边界条件，太阳辐照度Ra和环境温度Th随时间变化情况如图 3所示.

    在流体传热物理场中，出口与入口设置为开放边界，并选用静水压力补偿选项，模拟热流的流入或流出.室内空气的温度初始值与环境温度初始值一致，速度初始值为0.设置对流热通量来模拟箱体壁与环境之间的对流散热，对流热通量可表示为

    其中，h为对流传热系数，其值与箱体壁面处的温度和外部环境温度所得出的瑞利数有关[16]，可选定自然对流方式后由COMSOL内置方程自行计算.

    在湍流物理场中，同样设置出口与入口为开放边界，这有利于约束模型中的压力项.设置集热板为内壁，与壁边界一样选中无滑移选项，限制壁面处的速度为0.

    • 2.4.   网格与求解器

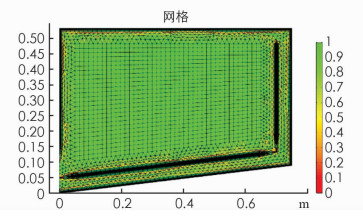
  • 网格划分采用混合型网格，在干燥室中间部分采用结构化网格，在近壁面的位置采用带有边界层的非结构化网格.网格颜色代表网格质量，网格质量越接近1，说明网格质量越好.由图 4可以看出：混合型网格减少了计算量，且不会影响网格质量与计算结果.

    求解器选用直接线性求解器PARDISO，对内存要求较小，且支持并行运算，适合多物理场的模拟.为了保证模拟结果的准确性，设置相对容差为0.005，其他设置保持默认状态即可[17].

3.   模拟结果与实验验证

    3.1.   模型验证

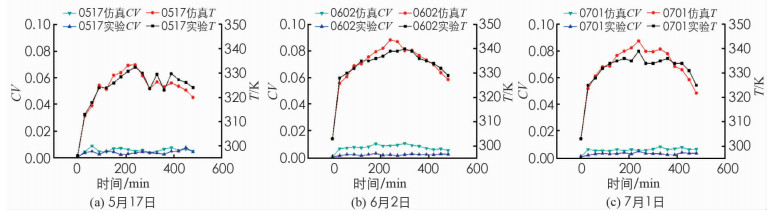
  • 为了说明干燥室内温度分布的均匀情况，本文引入相对标准偏差

    式中：S为标准偏差；T为干燥区域采样点(图 2中P1-P9点)的温度平均值；n为采样点个数(本文中n为9)；Tj为第j个采样点的温度值；通过计算不同时间的CV值来评价温度场的均匀度，CV值越小，温度场均匀性越高.由图 5下方两条线段可以看出在不同天气条件下CV值从9：00-17：00都远远小于1，说明温度场的实验值和模拟值的均匀性都较好，可在9个采样点中取某一点数据的分析结果来代表整个区域.取P5点的温度模拟值与实验值进行对照，温度数据随时间的变化情况如图 5上方两条线段所示，模拟值T在某些时间段略高于实验值的主要原因是数值模拟时，忽略了铝合金框架和有机玻璃板的比热容以及外界风速影响.

    计算温度模拟值和实验值的相关系数R2和均方根误差RMSE作为判断依据，R2越接近1说明二者相关性越好，RMSE远小于各采样点的值说明误差较小，二者的计算公式[19]：

    其中Xi为实验值；X为实验平均值；Yi为模拟值；为模拟平均值.

    干燥室中温度模拟值和实验值随时间的变化曲线如图 5所示.干燥室内温度可在接受日晒后30 min内快速升温，在温度达到一个较为稳定值后随辐照度缓慢变化.实验与模拟的温度峰值都出现在210 min左右，在一般的晴朗天气下，干燥室温度达到稳定后模拟值可维持在45 ℃~75 ℃(318.15~348.15 K)之间，可将外部空气升温15 ℃~35 ℃.由采样点的数据算出3 d的实验值与模拟值之间的决定系数R2与均方根误差RMSE(表 1)，说明该模型能够较好地预测干燥箱内温度，并且在晴朗天气下的预测结果比多云好，主要是因为本文对辐照度与环境温度进行了平均处理，分段时间减小会得到更加精确的结果，但计算量也会大大增加.

    • 3.2.   温度分布

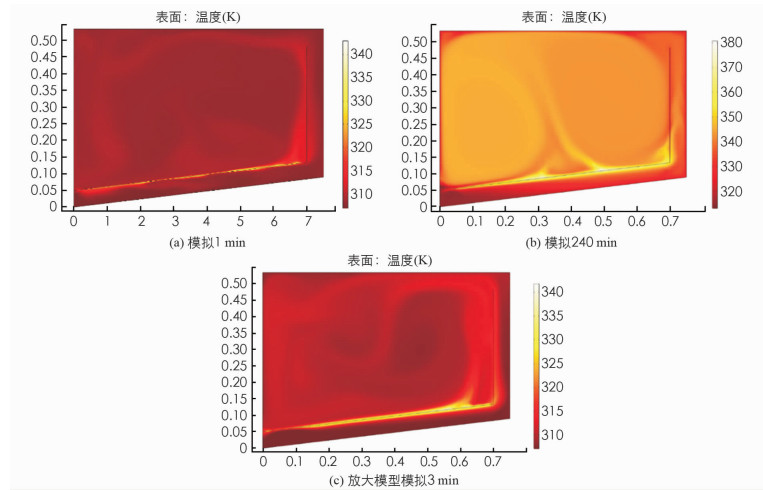
  • 由任意一天的模拟云图可以得到干燥箱中整个干燥时间的自然对流传热过程.从图 6(a)可以看出在开始加热时，主集热板上表面的热空气与集热板之间的温差大，对流传热较快，并且由于粘滞力的作用沿集热板上浮，主集热板下表面的热空气通过外部流道流入干燥室，此时干燥室内空气流动剧烈，热流场变化迅速，干燥室中冷热空气混合，有利于干燥室快速升温.由稳定时的云图 6(b)可看出，干燥室水平中间列P2，P5，P8附近温度略高于其他位置.从集热板的传热效果可以看出集热板内外表面同时和空气进行了对流换热，相当于主、侧集热板构成的外部流道使集热板与空气的换热面积增加了一倍，并且加剧了干燥室内空气流动.由图 6(c)可看出将数学模型按比例放大后，干燥箱升温需要更长的时间，但集热板与空气的传热效果与小型模型相似，说明此种外部流道结构可以适用于大型温室型干燥装置的结构改进.

    • 3.3.   流场分布

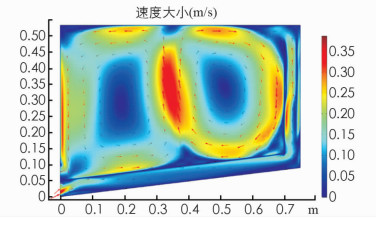
  • 在仿真进行到240 min时，温度场达到一个较为稳定的情况，此时流场相对稳定，在辐照度不发生剧烈变化的前提下，稳定后的流热场具体分布变化不大，仅有数值的大小不同，如图 7所示的流场情况在整个干燥过程中占大部分时间. 图 7中的小箭头表示流体流动的方向，可以看出室外空气通过入口进入外部流道，在经过集热板下表面初步加热后进入干燥室，空气在干燥室中形成两个大涡，涡中心的流速很低，而水平中间列P2，P5，P8列的速度略高于其他区域.由此可以看出，干燥时物料托盘应该放置于水平中间列P2，P5，P8等流速较高处，使得物料可以得到充分加热，蒸发出的水汽也可以由此处流速较高的空气带走.根据温度流场变化情况可以制定相对应的干燥物料种类、物料厚度、干燥时间等干燥工艺.

4.   结果与讨论

  • 本文研究了一种新型太阳能干燥箱在自然对流模式下的工作情况，通过COMSOL Multiphysics5.4多物理场仿真软件求解了流热场耦合数学模型，通过输入不同的辐照度以及环境温度初始条件，可以预测不同天气情况下干燥箱内的流热场具体分布.由于忽略了外部环境风速、湿度等因素对干燥箱内的影响，本文所构建的模型不适合大风、雨后等特殊天气的模拟，对于特殊天气的模拟研究还有待进一步探索.

    由干燥箱内温度场的模拟值与实验值建立了均匀性评价指标CV值随时间的变化曲线，由变化曲线可看出在整个实验过程干燥箱内温度分布较为均匀.在不同天气情况下得出温度模拟值与实验值的R2分别为0.967，0.978，0.956；RMSE分别为2.289，1.821，1.940，说明本文建立的预测模型较为准确.在接受日晒30 min内升温较快，随后缓慢升温，在一般晴朗天气下干燥装置可将外界空气升温15 ℃~35 ℃.干燥室内温度可维持在45 ℃~75 ℃之间，满足大多数农作物的干燥需求.

    本文建立的数值模拟模型可代替费时费力的人工试验，其模拟出的结果可以方便地优化干燥工艺，防止由于天气变化导致干燥效率和干燥品质的降低，从而达到更好的干燥效果.在将模型等比例放大后得到的模拟结果可对大型温室的结构改进提供参考.

参考文献 (19)

目录

版权所有：西南师范大学学报(自然科学版)

地址：重庆市北碚区西南大学 电话：023-68252540，68254576，68254478 电子邮箱：xbbjb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回