-
随着移动互联网和社交网络的快速发展,海量数据呈爆炸式增加. 不同于以往的传统数据,大数据具有数据量巨大、种类繁多、产生和处理速度快以及价值密度低等特性[1-2]. 大数据蕴含丰富的信息,在智能制造、金融服务、生物医疗以及公共安全等领域具有广泛的应用,由于传统数据的计算能力与查询引擎等已无法满足大数据处理需求,因而大数据查询技术应运而生[3]. 大数据查询技术拥有巨大的商业应用潜力,但同时也面临着巨大的挑战.
为了满足用户多样性和高效率的查询需求,研究人员开发了多种数据查询方法. 对于大数据查询,主要通过任务调度,查询算法和数据结构的优化方法或近似查询处理来提高性能. 不同于前者,近似查询处理获得的是与实际结果偏差可忽略的近似结果,同时该类方法能够在较短的响应时间内满足用户的大数据查询需求,节省了处理资源,提高了查询性能[4]. 近似查询处理方法主要分为采样方法[5]、基于概率模型方法[6]和基于聚类方法3种. 采样方法在查询完整性与效率之间进行权衡,概率模型方法为了提高查询速度而设置的置信区间不利于查准率提高. 聚类是一种流行的数据挖掘方法,根据不同的方式对数据点进行划分,保证同一类中的数据点尽可能相似,且与其他类中的数据点尽可能不同[7]. 文献[8]提出一种基于K-Medoids算法的潜在加速技术,该算法使用Apache Spark框架作为并行和分布式计算环境,提高了数据的聚类效率和精度. 文献[9]提出一种基于可伸缩的K近邻(KNN)查询处理方法,该方法基于数据空间的概率变换,导出一种用于多变量数据的空间变换组织结构来简化查询处理. 文献[10]提出一种平衡最近邻查询方法,该方法根据用户的偏好评估聚类效果,并返回一个具有普遍性和现实性的邻域,在查准率、查全率和效率之间取得较好的平衡.
对于因应用场景广泛分布而产生的多样性大数据,现有的空间查询处理方法不足以在大数据环境中提供快速准确的结果. 为了降低查询的执行时间和误差,本文提出一种应用在Apache Spark上的动态聚类模型来提高大空间数据查询的可伸缩性和性能. 查询方案包括数据预处理、数据聚类和查询3个阶段:在预处理阶段,为了提高数据的可靠性,对输入数据进行离散化操作;在数据聚类阶段采用划分和层次聚类相结合的聚类算法,对空间数据集进行动态分布式聚类,保证在管理大量数据时内存和时间复杂性可以足够低;在查询阶段,采用K近邻查询方式,获得高精度和高效率查询结果. 本文的创新之处在于提出了适用于大数据空间查询处理的动态聚类模型. 动态聚类不需将聚类簇头设置为静态的,而是动态改变聚类簇头数量来寻找最佳簇头,从而提高大数据的查询处理能力.
全文HTML
-
K-medoids是一种基于划分方式的聚类算法[11],具有操作简单、局部搜索能力强等优点. 该算法以数据样本中的原始样本作为簇中心,通过欧式距离度量函数来度量样本之间的相似性,而后采用迭代、贪婪的方法将样本空间中的数据聚集为K个簇.
K-medoids聚类的基本思想是:假定待聚类分析的数据样本集合为X,X={X1,X2,…,Xn}为n个节点的集合,其中Xi={xi1,xi2,…,xim}为m维数据点. 首先从样本集合X中选择k个节点作为初始类簇中心点C={Ci|i=1,2,…k},然后判断其他节点到中心的距离dij,并将其分配到对应的类中. K-medoids聚类的目标函数为当前类中所有其他点到该中心点距离之和的最小值
式(1)中:Xj表示数据样本集中的样本数据,Xic表示第i类的簇中心.
K-medoids聚类算法选取类中实际样本数据作为簇中心,从而降低了算法对离群点和孤立点的敏感性.
-
CURE(Clustering Using Representatives)算法[12]是一种自下向上的层次聚类算法,该算法的基本思想是对于每个簇,采用多个代表点来表征一个簇,然后不停地将相邻的两个簇进行合并,直到簇的数目达到预定的阈值. 由于传统聚类算法获得的是球状、大小相等的簇,对异常数据比较脆弱,因此CURE采用多个点表征簇的方式有效克服了上述问题,是一种针对大型数据库的高效聚类算法. CURE聚类算法的基本步骤:①从大数据集中抽取样本数据集;②将样本数据集进行划分;③对每个划分进行局部层次聚类;④选取代表点,对相邻的两个簇进行合并,利用收缩因子更新代表点;⑤通过随机取样剔除孤立点,去掉聚类过程中增长缓慢的簇;⑥将最终的聚类簇进行标记.
1.1. K-medoids聚类
1.2. CURE聚类
-
在大数据查询问题中,大部分方法都是采用将数据变小的方式,然后利用不同的查询技术找到精确的查询结果. 为了提高大数据空间查询处理的效率和可伸缩性,本文提出一种基于划分和层次动态聚类算法的大数据查询模型,该模型在Spark上方作为分布式计算框架运行,主要分为数据输入和预处理、基于划分和层次动态聚类和用户查询策略3个阶段. 对于空间数据集来说,本文提出的基于划分和层次聚类算法是动态的,这是因为该算法先采用K-medoids聚类快速生成一定数量的子簇,然后使用改进的CURE聚类以整体相似度的聚类质量评价标准来动态集合聚类数目. 由于全局聚类数量是动态的,不需要预先输入正确聚类的数量,从而解决了K-medoids算法对初始聚类中心敏感和过于依赖的问题.
-
由于输入的空间数据集过于庞大和复杂,以至于人类无法有效地借助计算工具来提取有用的信息,因此研究人员提出了Spark等技术来处理大数据并将其转变为有意义的信息. 为了解决空间数据集结构繁杂、数量巨大的问题,在预处理前使用映射器将输入数据转换为RRD(Round Robin DataBase)格式,并将数据集划分为多个子集,存储在一组机器节点中. 对单个节点上的子集数据进行预处理操作,主要包括填补缺失值、处理噪声、规范化数据以及减少数据冗余. 预处理阶段可以在多个并行操作中完成,目的是对输入数据进行离散化,避免数据不一致,提高数据的可靠性.
-
为了提高数据查询的准确性和效率,本文提出了基于划分和层次动态聚类算法. 该阶段主要分为3步:数据局部聚类、数据约简和全局聚类. 首先,使用分布式K-medoids聚类算法对每个节点上经过预处理的数据进行聚类,获得多个簇. K-medoids算法作为一种划分聚类方法,能够有效处理异常数据和噪声数据,具有良好的鲁棒性.
其次,对聚类后的数据进行约简. 该部分使用数据约简技术来获取数据集的缩减表示形式,该表示形式的体积要小得多,但仍保持原始数据的完整性. 大多数数据约简技术如采样、数据压缩、数据离散化等方法只关注数据集的存储大小,而不关注隐藏在其中的有效信息. 为了挖掘数据集中的重要信息,本文采用一种基于簇的形状和密度的有效缩减技术[13],该技术关注于创建簇的形状和密度,簇的形状由其边界点表示,密度由平均密度值表示. 在每个机器节点上执行缩减过程,该过程的目的是建立一个由簇的边界及其密度信息构成的约简集ϕ,该约简集ϕ可以看作节点i上的局部簇Mi.
簇边界点可以看作是聚类的边界,获得边界是一个困难的问题. 边界点在视觉上可以表征为一侧限制在密集区域而另一侧限制在空白区域的点. 为了检测聚类的边界点,文中应用了平衡矢量算法.
给定一个聚类簇C⊆
$\mathfrak{R} $ m≡{p1,p2,…,pm},则对于聚类簇C内的任一点p,其ε邻域NεC(p)定义为式(2)中:dist(p,pi′)表示点p与pi′之间的距离.
当判断点p是否为边界点时,需要确定p邻域中密集最小区域的方向. ε邻域NεC(p)内点pi′到点p的位移矢量定义为
$\overrightarrow{v}$ p矢量的方向指向p邻域中密度最小的区域. 由于本文仅关注$\overrightarrow{v}$ p矢量的方位指向,对其矢量长度不作考虑,因此p点处的平衡矢量可以定义为边界点由布尔判断表示为
聚类簇C的边界可以由一组边界点BC表示为
对于C内的任意一点q,必定满足以下条件
式(7)中:pj是BC中q的最近邻居. 同时,还可以定义BC的最小封闭超立方体为
在本文方法中,主要关注簇的形状和密度. 簇的形状由边界点BC表示,它的密度可以用一个描述簇内各个区域密度的平均值dC来表示. 为了简化计算,在构造简约集时使用簇C的基数m=|C|代替dC.
根据上述求解的簇C边界及基数m,以及给定的平均密度dC,在节点上执行缩减过程,利用BC最小封闭超立方体内的生成点来构造一个与C簇相似的簇C′,生成点只有满足条件(7)才能被添加到C′中. 反复进行这个过程,直到簇C′满足基数m.
最后一步则是通过层次聚合方式将局部聚类合并,合成全局聚类. 在合并过程中采用改进的CURE方法. 该方法采用多个点来代表一个簇,因为代表点的收缩经常会导致错误的聚类结果,所以舍弃了原算法中代表点收缩的过程. 本文选择medoid点与簇的边界点作为簇的代表点,能够准确地刻划出簇的物理几何形状. 两个簇之间的合并采用距离度量准则进行考量,簇之间的距离定义为两个簇代表点之间的最小距离,即
式(9)中:urep是簇u的代表点,vrep是簇v的代表点.
在聚类合并完成之后,采用整体相似度评价合并前后的聚类质量,如果合并结果是聚类质量下降,就取消合并. 为了提高聚类质量,将位于每个节点的簇的代表点与其邻域节点交换,计算其相关度,便于确定适合合并的簇. 重复这些步骤直到生成所有全局聚类.
-
用户查询策略分为查询语句分析和数据查询2个部分. 首先,采用词法分析器对用户查询语句进行词法分析以检查语法,并根据输入文本字符串流的结构,将其划分为可组成连贯短语的词组,从中构造标记. 然后根据提出的标记词组进行数据查询. 两个最常见的空间查询方法是K近邻(KNN)查询和窗口查询. KNN查询检索出相对于查询用户位置最近的K个对象,而窗口查询则显示所请求窗口内以查询位置为中心的所有对象.
2.1. 预处理阶段
2.2. 基于划分和层次的混合聚类
2.3. 用户查询策略
-
为了验证本文所提大数据查询方案的性能,采用NYC Taxi数据集[14]进行实验,以聚类错误率和执行时间为评估标准对结果进行分析. 所有测试在HP ProLiant DL180 Gen9服务器中实施,其处理器为Intel Xeon E5-2620v3 @ 2.4 GHz(12个CPU),RAM为64 GB,SSD硬盘为3 * 1TB(Raid 5). 所有算法均使用Java编程语言编写,JDK版本为1.8. 本文所提出的模型在Hadoop 2.7.1和Spark 2.2.0上运行,以进行分布式并行处理.
NYC Taxi数据集是目前公开提供的最全面的旅行记录数据集之一. 截至到2015年,在线发布了超过10亿个纽约出租车记录. 每个记录给出了出租车的详细行车位置数据,包括等级、执照、供应商编号、比率代码、上车时间、下车时间、乘客数量、行车时长、行车距离、上车经纬度坐标、下车经纬度坐标等属性信息. 为了评估模型的性能,将出租车数据集划分为不同大小的可变数据集(500~3 000万条记录;800 MB~5 GB). 所有实验中将上车位置视为二维空间查询对象.
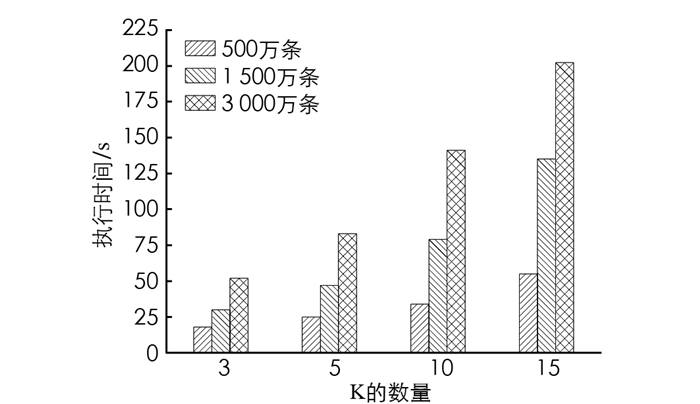
第一组实验根据不同数据集大小的平均执行时间来评估不同查询的性能. 通过设计的不同KNN搜索查询测试用例来评估,图 1给出了KNN搜索查询的性能结果. 对于一个给定的查询点,执行10个测试查询. 使用采样方法从高密度区域中选择不同的查询点. 从图 1中可以看出,KNN查询检索引擎的平均执行时间随着邻居数K和数据集行数的增加而增加.
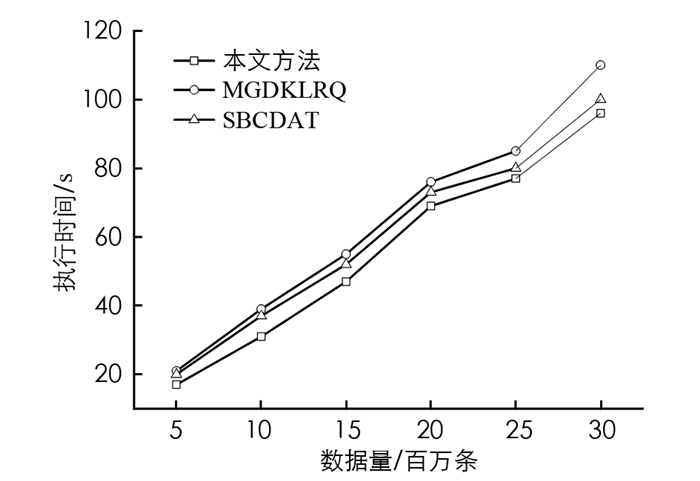
第二组实验使用在第一个实验中的相同数据集,对比本文提出方法、MGDKLRQ[15]和SBCDAT[16]3种方法的平均执行时间. 在测试中,对于一个给定的查询点,执行10个测试查询以便从给定查询点找到K个最近的上车位置,K=5. 图 2给出了3种方法的对比测试结果. 从图 2中可以看出,本文提出模型所需要的执行时间最少,表现出的查询性能最优. 本文提出模型的优越性在于它采用了基于划分和层次聚类算法构建全局聚类的事实. 因此,与其他方法相比,本文方法生成的簇总数少得多,在少量几个簇中进行数据搜索的时间花费较少,故而查询的执行时间最低.
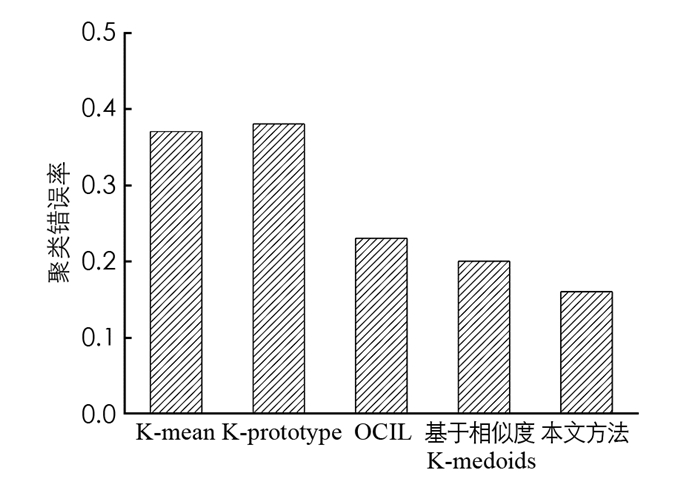
第三组实验对比了现有聚类算法技术和本文所提出算法的性能结果,从聚类误差率(clustering error,CE)的角度对结果进行了分析和评价. 聚类误差率是在最优排列下匹配结果与真实样本之间的误差,其定义为
式(10)中:qi和pi分别表示聚类后的类标签和真实类标签,map(·)为映射函数,δ(x,y)为一增量函数,当x=y时,δ(x,y)=1,否则为0.
图 3给出了现有聚类算法如K-means、K-prototype、对象聚类迭代学习(OCIL)和基于相似度的K-medoids等几种聚类方法的CE测试结果. 从图 3中可以看出,本文提出的聚类方法的聚类误差率最低,证明了该聚类模型的优越性,进而显著影响了最终查询方案的质量.
-
本文提出一种基于动态分布式聚类算法的大数据查询处理方法,用于解决现有空间查询处理方法在多样性大数据环境中执行时间长和查询结果精确度低的问题. 实验结果表明,本文提出的方法明显优于对比查询方法,在空间数据查询处理中可以获得高质量的结果.



 下载:
下载: