-
文献[1-2]提出了广义自回归条件异方差(GARCH)模型,该模型主要用于刻画资产收益率的波动规律. 文献[3-4]将GARCH同多种传统模型进行实证比较,结果表明GARCH能更为准确地反映我国某些市场的波动情况. 后续学者根据市场特征和需求的不同对GARCH进行了推广研究,并演化出了一系列GARCH族模型[5].
目前,用于估计GARCH模型参数的方法多种多样. 文献[6]将类极大似然(QML)法用于GARCH和ARMA-GARCH模型的参数估计;文献[7]将QML法扩展到一系列多维GARCH类模型,且实证表明其能很好地刻画汇率序列的波动. 虽然文献[8]指出QML估计对数据分布具有一定的容错性,但其对异常值很敏感,少量异常值就会对QML估计产生巨大的影响,也即QML估计并不稳健,其次,QML法还要求序列4阶矩存在,而金融收益率时序列分布往往呈现出“尖蜂厚尾”的特点,难以满足该条件. 由此,文献[9]提出了较为稳健的偏差绝对值最小(LAD)法. 文献[10]提出了基于传统GARCH模型的分位数回归估计(QR)法,并证明了该估计的一致性. 虽然QR估计一定程度上减少了数据尖峰厚尾所造成的估计误差,但风险水平的选取将直接影响到QR估计的结果. 因此,文献[11]将复合分位数回归(CQR)应用于估计高频数据的GARCH参数,数值模拟结果显示CQR估计较QR估计更为精确有效. CQR通过综合考虑多个风险水平下的条件QR使得估计更为稳健有效,但应对不同的市场损失情况应当赋予不同程度的损失,故文献[12]考虑加权复合分位数回归(WCQR)法,其通过极小化WCQR参数估计的渐进方差得到权重值,对于不同分位数回归给予不同的权重,以此得到更加稳健有效的估计.
近年来,受文献[13]提出的两步QR思想的启发,文献[14]提出了GARCH模型的混合QR估计,该估计主要分为两步:首先计算QML估计下的条件标准差拟合序列,接着将此条件标准差拟合序列的倒数作为QR损失的权重得到估计,数值分析表明混合QR估计可以削弱极端波动的影响,得到更为精确有效的估计;文献[15]还将上述混合QR估计用于探究GARCH-X误差模型,数值模拟显示出该混合估计在大样本下表现最优. 本文进一步将混合估计扩展到CQR,结合WCQR思想,由此提出二次加权分位数回归(BWCQR)技术. 数值模拟及实证分析表明利用BWCQR估计GARCH模型参数在一定准则下相较已有估计技术更加合理有效.
全文HTML
-
记yt表示某资产第t天的收益率,则标准GARCH(p,q)模型为
其中:扰动序列{ηt,t≥1}为独立同分布的随机变量序列;vt为yt的条件标准差,vt=Var(yt|
${\mathscr{F}}$ t);${\mathscr{F}}$ t表示由{ys;s≤t}生成的σ-域. 记参数α=(α1,…,αq)T,β=(β1,…,βp)T,γ=(αT,βT)T且γ≥0,对应的真值分别为α*=(α1*,…,αq*)T,β*=(β1*,…,βp*)T,γ*= (α*T,β*T)T.对应GARCH(p,q)模型的条件τk分位数为
其中ξk*为扰动序列{ηt,t≥1}的第τk个真实分位数,也即满足P(ηt ≤ξk*)=τk.
GARCH模型的CQR估计[11]为
其中:分位数水平τk=
$\frac{k}{1+K}$ ,k=1,…,K;条件分位数qt(θk)=vt(γ)ξk由式(1)可得;τk水平下损失函数定义为ρτk(u)=u(τk-I)(u < 0),其中I为示性函数;参数空间Θμ的定义见假设1. 记参数ξ=(ξ1,…,ξK)T,θk=(ξk,γT)T,θ=(ξT,γT)T,对应的真值分别为ξ*=(ξ1*,…,ξK*)T,θk*=(ξk*,γ*T)T,θ*=(ξ*T,γ*T)T.注意到,当p,q≥0时,本文初值取为y0=…=y1-q=y1,
$\hat v$ 02=…=$\hat v$ 1-p2=y12,取定初值后的vt2(γ)对应为$\hat v$ t2(γ)=$1+\sum_{i=1}^{q} \alpha_{i} y_{t-i}^{2}+\sum_{j=1}^{p} \beta_{j} \hat{v}_{t-j}^{2}(\boldsymbol{\gamma})$ .将文献[12]提出的WCQR扩展至GARCH模型
其中:
$\hat q$ t(θk)为给定初值下的条件分位数$\hat q$ t(θk)=$\hat v$ t(γ)ξk;ωk表示τk分位数水平下损失函数对应的权重,对任意1≤k≤K有ωk> 0,且$\sum_{k=1}^{K}ω_k=1$ . 关于权重ωk的选取详见注2.将文献[14]提出的混合QR加权思想扩展到CQR,由此衍生出估计
其中
$\hat v$ t为给定初值下CQR估计的条件标准差,$\hat v$ t=$\hat v$ t($\tilde γ$ n),$\tilde γ$ n由式(2)计算可得.将式(3)和式(4)相整合,即可得到本文提出的BWCQR估计
-
在给出BWCQR估计的渐进性质之前,须引入一些记号和模型假设:记向量a的欧几里得范数为‖a‖;C表示在不同的计算过程中不尽相同的任一正数;定义矩阵A=(aij)的欧几里得范数为‖A‖ =
$\sum_{i,j}$ |aij|;V表示一广义可积随机变量;{St}表示一平方可积非负平稳遍历过程且满足St∈${\mathscr{F}}$ t-1;变量ρ满足0 < ρ < 1;ρτk(u)关于u的导数为ψτk(u)=τk-I(u <0).假设1 模型的真值θ*为Θμ的内点,其中参数空间Θμ定义为
其中实数μ∈(0,1)且使得θ*∈Θμ.
假设2 令多项式A(x)=
$\sum_{i=1}^{q}$ αi* xi,B(x)=1-$\sum_{j=1}^{p}$ βj*xj,对p,q>0有αq*>0,βp*≠0. 多项式A(x)和B(x)没有公因子.假设3 (i) 扰动ηt满足E(ηt2) < ∞;(ii) 记ηt的累积分布函数为F,对应的密度函数为f. f可积且对1≤k≤K满足f(F-1(τk))>0,且有supx|f(x)|≤C1,supx|f′(x)|≤C2,其中实数C1,C2>0,f在ξk*的邻域内连续.
假设4 矩阵
$E\left(\frac{\partial q_{t}\left(\boldsymbol{\theta}_{k}^{*}\right)}{\partial \boldsymbol{\theta}} \frac{\partial q_{t}\left(\boldsymbol{\theta}_{k}^{*}\right)}{\partial \boldsymbol{\theta}^{\mathrm{T}}}\right)$ 为正定矩阵.定理1 在假设1-3满足的条件下,有n→∞时
$\hat{\boldsymbol{\theta}}_{n} \stackrel{p}{\longrightarrow} \boldsymbol{\theta}^{*}$ .为了简便,记vt=vt(γ*),
$\tilde v$ t=vt($\tilde {{\mathit{\pmb{γ}}}}_n$ ),$\hat v$ t=$\hat v$ t($\tilde {\mathit{\pmb{γ}}}_n$ ),其中$\tilde {\mathit{\pmb{γ}}}_n$ 表示复合分位数的参数估计(CQRE);qt(θk)=ξkvt(γ)和$\hat q$ t(θk)=ξk$\hat v$ t(γ)分别表示未给定初值和给定初值τk水平下的条件分位数. 文献[10]的推论A.1-A.7给出了qt(θk),$\hat q$ t(θk),vt(γ)和$\hat v$ t(γ)及其导数的相关性质,本文中简记为A.1-A.7.证明 分别定义
其中lk(θ)=ρτk(yt-qt(θk)),
$\hat l$ k(θ)=ρτk(yt-$\hat q$ t(θk)),qt(θk)=ξkvt(γ),$\hat q$ t(θk)=ξk$\hat v$ t(γ). 为了方便,定义dt(θk)=qt(θk)-qt(θk*),$\hat d$ t(θk)=$\hat q$ t(θk)-$\hat q$ t(θk*),ηtk=ηt -ξk*.本文主要证明定理2及推论3,定理1不作详细证明. 关于定理1可参考文献[15]中定理1的证明,分证四点即可:
1)
$\sup\limits _{\boldsymbol{\theta} \in \Theta_{\mu}}\left|\hat{S}_{n}(\boldsymbol{\theta})-S_{n}(\boldsymbol{\theta})\right|=o_{p}(1)$ ;2)
$\sum_{k=1}^{K} \omega_{k} E\left(\sup\limits _{\boldsymbol{\theta} \in \Theta_{\mu}} v_{t}^{-1} l_{k}(\boldsymbol{\theta})\right)<\infty$ ;3)
$\sum_{k=1}^{K} \omega_{k} E\left(v_{t}^{-1} l_{k}(\boldsymbol{\theta})\right)$ 在θ*处有唯一最小值;4) 对任一θ#∈Θμ,当
$\ell$ →0时有$\sum_{k=1}^{K} \omega_{k} E\left(\sup\limits _{\boldsymbol{\theta} \in B_{\ell}(\boldsymbol{\theta} ^{\#})} v_{t}^{-1}\left[l_{k}(\boldsymbol{\theta})-l_{k}\left(\boldsymbol{\theta}^{\#}\right)\right]\right)$ →0,其中B$\ell$ (θ#)={ θ#∈Θμ:|θ#-θ| <$\ell$ }表示以θ#为中心$\ell$ 为半径的邻域.定理2 在假设1-4满足的条件下,有
$\sqrt{n}\left(\hat{\boldsymbol{\theta}}_{n}-\boldsymbol{\theta}^{*}\right) \stackrel{d}{\longrightarrow} N\left(\bf{0}, \boldsymbol{D}^{-1} \boldsymbol{C D}^{-1}\right)$ ,其中矩阵C,D分别为:注1 当K=1,ω= 1 且vt=1时,定理2退化为QR估计的渐进性质,详见文献[10]定理2;当K=1且ω= 1 时,定理2退化为混合QR的渐进性质,详见文献[15]定理2;当ω= 1 且vt=1时,定理2退化为CQR的渐进性质,详见文献[11]定理2.
引理1 在假设1-3满足的条件下,定义δ=
$\sqrt n$ (θ-θ*),有其中Gn(θ)=Sn(θ)-Sn(θ*),
$\tilde G$ n(θ)=$\tilde S$ n(θ)-$\tilde S$ n(θ*),$\hat G$ n(θ)=$\hat S$ n(θ)-$\hat S$ n(θ*).证明
可分别证
$\tilde R$ 1n(θ)=op(|δ|)与$\tilde R$ 2n(θ)=op(|δ|2).1) 分别对dt(θk)及
$\hat d$ t(θk)进行泰勒展开注意到,对∀τ∈(0,1)有ρτ(x)≤|x|. 由ρτ(x)的Lipschitz连续性及式(6),有
其中θ′为介于θ*与
$\boldsymbol{\theta}^{*}+\frac{\boldsymbol{\delta}}{\sqrt{n}}$ 之间的p+q+K维向量,θ′k为θ′的p+q+1维子向量(ξ′k,γ′T)T. 由A.4及|vt2|≥1不难得到因此,由式(8)及A.2有
2) 定义
由文献[16]有等式
定义ηtk=ηt-ξk*,对∀c>0,ψτ(x)=ψτ(cx)且由式(9)可以得到等式
将式(10)和式(11)代入
$\tilde R$ 2n(θ)有$\tilde R$ 2n(θ)$\triangleq \widetilde{\Pi}_{1}$ (δ)+$\widetilde{\Pi}_{2}$ (δ)+$\widetilde{\Pi}_{3}$ (δ)+$\widetilde{\Pi}_{4}$ (δ),其中将式(6)代入
$\widetilde{\Pi}_{1}$ (δ),由A.4及|ψτ(x)| < 1有据ψτ(x)的定义对其应用Fubini定理及泰勒展开有
其中ξk1介于ξk*和ξk*
$\tilde v$ tvt-1之间. 故由假设3、重期望、A.2与A.7及式(6)可得注意到|
$\tilde B$ tk|≤2,由此同对$\widetilde{\Pi}_{1}$ (δ)的讨论类似,可以得到$\widetilde{\Pi}_{3}$ (δ)=op(|δ|).最后考虑
$\widetilde{\Pi}_{4}$ (δ). 由Fubini定理及泰勒展开有其中ξk2=ξk*
$\hat v$ t(γ*)vt-1+vt-1$\hat d$ t(θk)s2和ξk3=ξk*+vt-1dt(θk)s3,0 < s2,s3 < s≤1. 故由假设3、式(6)及A.2与A.4可得引理2 在假设1-3满足的条件下,有
证明 引理2的证明同引理1的证明类似
据文献[17]定理3.1和式(9)易证K1n(δ)=op(|δ|)与K2n(δ)=op(|δ|2).
引理3 在假设1-3满足的条件下,有
其中
证明 由式(9)有
对R1n(δ)泰勒展开:R1n(δ)=-δTCn-δTK3n(θ′)δ,其中
其中θ′为介于θ*与θ*+
$\frac{\boldsymbol{\delta}}{\sqrt{n}}$ 之间的p+q+K维向量,θ′k为θ′的p+q+1维子向量(ξ′k,γ′T)T. 由文献[10]A.2及St为二阶可积广义平稳遍历过程可得Var(K3n(θ′))→0,因此K3n(θ′)=op(1),也即R1n(δ)=-δTCn+op(|δ |2).定义Btk=Btk1+Btk2,其中
对R2n(δ)泰勒展开有R2n(δ)
$\triangleq$ K4n(δ)+K5n(δ)+K6n(δ)+K7n(δ),其中对E(Btk1|
${\mathscr{F}}$ t-1)应用Fubini定理及泰勒展开,则K4n(δ)=$\frac{1}{2}$ δTDnδ+δT${{{{\mathbf{\Pi}}}}}$ 1n(δ)δ,其中0 < s′ < s≤1,由中值定理、文献[10]A.2及假设3,对∀ζ>0
当ζ→0时,式(14)趋于0. 也即对∀ε,λ>0,存在ζ0=ζ0(ε)>0使得对∀n≥1有P(
$ \begin{array}{c} \sup\limits_{\mid \boldsymbol{\theta}-\boldsymbol{\theta}^{*} \mid \leqslant \zeta_{0}} \end{array}$ ‖Π1n(δ)‖>λ) <$\frac {ε}{2}$ . 当n足够大时,θ-θ*=op(1),因此P(|θ-θ*|>ζ0) <$\frac {ε}{2}$ . 当n足够大时故K4n(δ)=
$\frac {1}{2}$ δTDnδ+op(|δ|2).对K5n(δ)进行放缩后
应用文献[15]引理3可得K5n(δ)=op(|δ|+|δ |2). 由文献[10]A.2及|Btk2|≤2、|Btk|≤2可分别得到K6n(δ)=op(|δ|),K7n(δ)=op(|δ|2),由此R2n(δ)=
$\frac {1}{2}$ δTDnδ+op(|δ|+|δ |2).定理2证明 结合引理1-3和定理1,同文献[15]中定理2的证明类似即可证明该定理.
推论1 在假设1-4满足的条件下,有
$\sqrt{n}\left(\hat{\boldsymbol{\gamma}}_{n}-\boldsymbol{\gamma}^{*}\right) \stackrel{d}{\longrightarrow} N(\bf{0}, \boldsymbol{U})$ ,其中U为D-1CD-1的右下角(p+q)×(p+q)维矩阵:其中Σ=
$\operatorname{Var}\left(\frac{1}{v_{t}} \frac{\partial v_{t}}{\partial {\boldsymbol{\gamma}}}\right)$ .注2 令
据推论1可知Σ与权重ω无关,因此在
$\sum_{k-1}^{K} \omega_{k}=1$ 及ω> 0 的条件下,通过极小化σ2(ω)即可得到权重向量ω的数值解.推论1证明 矩阵C可分为4块分块矩阵
其中:C11为K×K维矩阵,其(i,j)元素为ωiωj(τi∧τj-τiτj);C12为K×(p+q)维矩阵,其第i行向量为
$\sum_{j=1}^{K}$ ωiωj(τi∧τj-τiτj)ξj*$E\left(\frac{1}{v_{t}} \frac{\partial v_{t}}{\partial \boldsymbol{\gamma}^{\mathrm{T}}}\right)$ 且C21=C12T;C22为(p+q)× (p+q)维矩阵,C22=$\sum_{i=1}^{K}\sum_{j=1}^{K}$ ωiωj(τi∧τj-τiτj)ξi*ξj*$E\left(\frac{1}{v_{t}^{2}} \frac{\partial v_{t}}{\partial \boldsymbol{\gamma}} \frac{\partial v_{t}}{\partial \boldsymbol{\gamma}^{\mathrm{T}}}\right)$ .同样可以将矩阵D分为4块分块矩阵
其中:D11为K× K维对角矩阵,其第i个元素为ωif(ξi*);D12为K×(p+q)维矩阵,其第i行向量为ωif(ξi*)ξi*
$E\left(\frac{1}{v_{t}} \frac{\partial v_{t}}{\partial \boldsymbol{\gamma}^{\mathrm{T}}}\right)$ 且D21=D12T;D22为(p+q)×(p+q)维矩阵D22=$\sum\limits_{k=1}^{K} \omega_{k} f\left(\xi_{k}^{*}\right) \xi_{k}^{* 2} E\left(\frac{1}{v_{t}^{2}} \frac{\partial v_{t}}{\partial \boldsymbol{\gamma}} \frac{\partial v_{t}}{\partial \boldsymbol{\gamma}^{T}}\right)$ .注意到,在假设4及权重向量ω> 0 的条件下矩阵D,C均为严格正的可逆矩阵,矩阵D-1 CD-1的右下块(p+q)× (p+q)维矩阵U为
其中
经计算可得推论1成立.
-
将本文提出的BWCQR分为如下6个步骤:
(i) 运用式(2)计算出CQR估计
$\widetilde{\boldsymbol{\theta}}_{n}=\left(\widetilde{\boldsymbol{\xi}}_{n}^{\mathrm{T}}, \widetilde{\boldsymbol{\gamma}}_{n}^{\mathrm{T}}\right)^{\mathrm{T}}$ ;(ii) 据步骤(i)可计算出条件标准差序列
$\hat v$ t=$\hat v$ t($\tilde γ$ n),进而计算出扰动序列$\hat \eta_{t}=\frac{y_{t}}{\hat {v}_{t}\left(\tilde \gamma_{n}\right)}$ ;(iii) 对步骤(ii)中的
$\hat \eta$ t采用核光滑估计可以得到其密度函数f(·)的估计;(iv) 计算步骤(ii)中的
$\hat \eta$ t的τk经验分位数$\tilde ξ$ k*;(v) 据步骤(iii)和(iv)即可确定权重目标函数σ2(ω),由此可解得ω的非参数数值解
$\tilde {\boldsymbol{ω}}$ ;(vi) 将步骤(ii)中
$\hat v$ t和步骤(v)中$\tilde {\boldsymbol{ω}}$ 代入式(3)、式(4)及式(5),可得估计$\hat {\boldsymbol{θ}}$ n1,$\hat {\boldsymbol{θ}}$ n2和$\hat {\boldsymbol{θ}}$ n.
1.1. GARCH模型的BWCQR估计
1.2. 假设及定理
1.3. 参数估计步骤
-
基于GARCH(1,1)模型
利用蒙特卡洛数值模拟检验本文所提BWCQR方法在有限样本下相较QML,QR和CQR方法的稳健性和有效性. 数值模拟模型参数选取如下:
(i) 分别考虑扰动项序列ηt服从标准正态分布N(0,1),t(5)分布和t(3)分布;
(ii) 样本容量分别取n=300,500,1 000和1 500进行300次重复抽样;
(iii) 复合分位数回归模型中K值取5,9和19,QR估计的风险水平取0.3,0.5和0.7;
(iv) 本文采用估计量的偏差(Bias)、标准差(SD)和均方误差(MSE)作为估计的评价标准.
为了方便起见,分别将K时的
$\tilde {{\mathit{\pmb{θ}}}}$ n,$\hat {{\mathit{\pmb{θ}}}}$ n1,$\hat {{\mathit{\pmb{θ}}}}$ n2和$\hat {{\mathit{\pmb{θ}}}}$ n的估计方法记为CQRK,WCQRK1,WCQRK2和BWCQRK. 表 1-3给出了3种分布下的数值模拟结果.分析结果得到:
(i) 无论扰动序列的分布如何,对任一估计,随着样本量n的增大,MSE愈小;
(ii) 各类复合分位数估计对K值的敏感程度不强;
(iii) 样本规模n一定时,K越大,MSE越小,也即K取19时各类复合分位数回归估计最优;
(iv) 当扰动项服从正态分布时,QMLE最优;
(v) 当扰动项服从重尾分布时,总体而言,BWCQR估计明显优于WCQR1,略优于WCQR2,且随着K的增加BWCQR估计的竞争力愈强.
-
选取上证和沪深300股指作为研究对象,实证区间为2015年1月5日至2021年5月11日,共计1 544个样本数据. 记pt为第t交易日的收盘价,rt为百倍对数收益率:rt=100×(lnpt-lnpt-1).
表 4给出rt序列的描述性统计分析值. 均值大于0,说明股指整体趋势上行,且序列不服从正态分布、不独立同分布. 综上所述,足以表明rt序列具有典型的高峰厚尾特征. Ljung-Box检验Q统计量和ADF检验表明序列具有明显的长记忆性且平稳.
本文选用GARCH(1,1)对该时间序列进行建模分析,采用向前一步滚动窗口预测方法,并将2015年1月5日至2020年1月23日作为初始滚动窗口. 本文对rt分别采用QMLE,MLE-t和BWCQR19进行拟合,对应标准化残差序列的ARCH-LM检验通过率列于表 5. 表 5结果符合数值模拟结论,BWCQR估计明显优于QMLE和MLE-t.
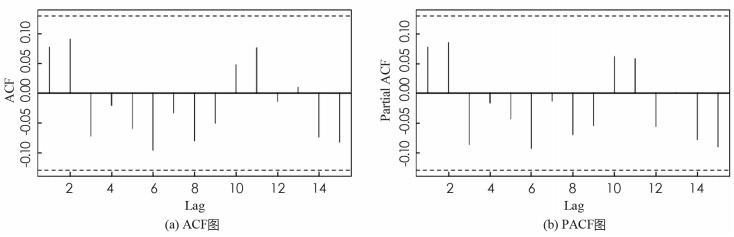
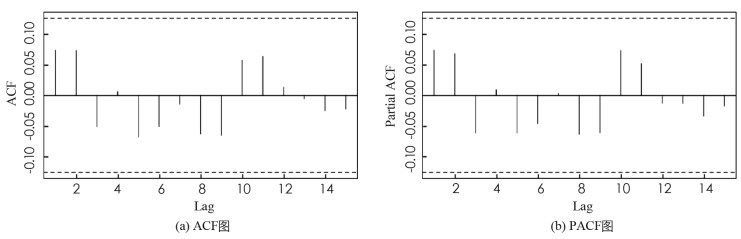
进一步,上证指数全序列和沪深300股指全序列在BWCQR估计下的标准化残差序列的自相关(ACF)图和偏自相关(PACF)图,如图 1,2所示,可见BWCQR估计下股指的标准化残差序列是白噪声序列,这再次验证了BWCQR估计的优良性.
2.1. 蒙特卡洛模拟
2.2. 实证分析
-
本文提出了GARCH模型的BWCQR估计并探究其大样本性质. 数值模拟结果显示:当扰动项序列服从正态分布时,QML估计略优于BWCQR估计;当扰动项序列服从厚尾分布时,BWCQR估计明显优于传统估计. 我们将提出的BWCQR拟合分析上证和沪深股指波动系统,结果表明BWCQR估计能更为合理有效地刻画股指时序的波动规律.



 下载:
下载: