-
上世纪80年代邓聚龙教授提出灰色关联分析理论[1],随后这一理论得到了极大的发展与应用[2-15]. 后1991年文献[2]根据邓氏灰色关联分析模型[3]研究了一类广义灰色关联分析模型,首次提出了绝对关联分析模型. 该模型有效解决了许多科研、生产中的实际问题,一直以来受到研究者的广泛关注. 在文献[2]提出的灰色绝对关联分析模型中,灰色关联算子起到了重要的作用. 但考虑到绝对关联度分析模型在做实际问题的定量分析时,存在因自然灾害、战争、疫情等意外因素的影响引起系统行为序列数据受到冲击干扰而失真的问题,本文采用均值化算子构造方法提出一种均值化的新关联算子并对灰色绝对关联度模型进行改进,并讨论该改进模型的性质和应用.
全文HTML
-
定义1 设原始数据的系统特征行为序列Xi={xi(1),xi(2),…,xi(n)},i=1,2,…,n,记均值
$\overline{x_{i}}=\frac{1}{n} \sum_{i=1}^{n} x_{i}(k)$ ,然后将折线{x(1)-$\overline{x_{i}}$ ,xi(2)-$\overline{x_{i}}$ ,…,xi(n)-$\overline{x_{i}}$ }记为Xi-$\overline{x_{i}}$ . 令$\overline{s_{i}}=\int_{1}^{n}\left(X_{i}-\right. \left.\overline{x_{i}}\right) \mathrm{d} t, \overline{s_{i}}-\overline{s_{j}}=\int_{1}^{n}\left(\overline{X_{i}^{0}}-\overline{X_{j}^{0}}\right) \mathrm{d} t$ ,又设序列Xi与Xj长度相同,则称$\overline{\varepsilon_{i j}}=\frac{1+\left|\overline{s_{i}}\right|+\left|\overline{s_{j}}\right|}{1+\left|\overline{s_{i}}\right|+\left|\overline{s_{j}}\right|+\left|\overline{s_{j}}-\overline{s_{i}}\right|}$ 为Xi与Xj的广义灰色均值关联度,简称均值关联度.定义2 设系统行为序列Xi={xi(1),xi(2),…,xi(n)},D为序列算子且
其中xi(k)d=xi(k)-
$\overline{x_{i}}$ ,k=1,2,…,n,则称D为均值零化算子,XiD为Xi的均值零化像,记为XiD=$\overline{X_{i}^{0}}=\left\{\overline{x_{i}^{0}}(1), \overline{x_{i}^{0}}(2), \cdots, \overline{x_{i}^{0}}(n)\right\}$ .
-
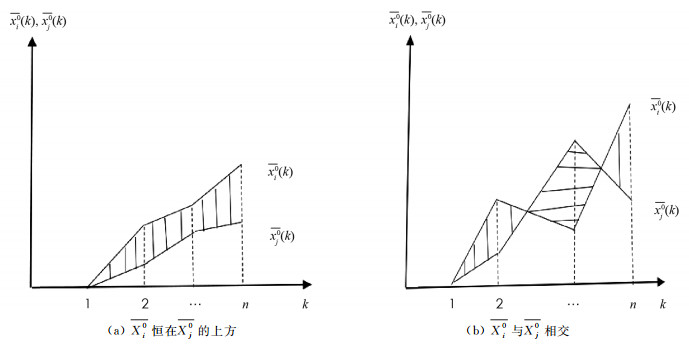
定理1 设系统行为序列Xi={xi(1),xi(2),…,xi(n)},Xj={xj(1),xj(2),…,xj(n)}的均值零化像分别为
$\overline{X_{i}^{0}}=\left\{\overline{x_{i}^{0}}(1), \overline{x_{i}^{0}}(2), \cdots, \overline{x_{i}^{0}}(n)\right\}$ ,$\overline{X_{j}^{0}}=\left\{\overline{x_{j}^{0}}(1), \overline{x_{j}^{0}}(2), \cdots, \overline{x_{j}^{0}}(n)\right\}$ ,令$\overline{s_{i}}-\overline{s_{j}}=\int_{1}^{n}\left(\overline{X_{i}^{0}}-\right.\left.\overline{X_{j}^{0}}\right) \mathrm{d} t$ ,则1) 当
$\overline{X_{i}^{0}}$ 恒在$\overline{X_{j}^{0}}$ 的上方,$\overline{s_{i}}-\overline{s_{j}}$ ≥0;2) 当
$\overline{X_{i}^{0}}$ 恒在$\overline{X_{j}^{0}}$ 的下方,$\overline{s_{i}}-\overline{s_{j}}$ ≤0;3) 当
$\overline{X_{i}^{0}}$ 恒与$\overline{X_{j}^{0}}$ 相交,$\overline{s_{i}}-\overline{s_{j}}$ 的符号不定.证 如图 1所示,在图 1(a)中,
$\overline{X_{i}^{0}}$ 恒在$\overline{X_{j}^{0}}$ 的上方,所以$\overline{s_{i}}-\overline{s_{j}}$ ≥0;图 1(b)中,$\overline{X_{i}^{0}}$ 恒与$\overline{X_{j}^{0}}$ 相交,所以$\overline{s_{i}}-\overline{s_{j}}$ 的符号不定. 由此可知定理1结论成立.定理2 广义灰色均值关联度
满足灰色关联公理中规范性、偶对称性与接近性.
证 1) 规范性:显然,
$\overline{ε_{ij}}$ ≥0,又|$\overline{s_{j}}-\overline{s_{i}}$ |≥0,所以$\overline{ε_{ij}}$ ≤1.2) 偶对称性:由|
$\overline{s_{j}}-\overline{s_{i}}$ |= |$\overline{s_{i}}-\overline{s_{j}}$ |知$\overline{ε_{ij}}$ =$\overline{ε_{ji}}$ 成立.3) 接近性:显然成立.
引理1 设Xi与Xj是长度皆为1的时距序列,而
$\overline{X_{i}^0}$ ={$\overline{x_{i}^0}$ (1),$\overline{x_{i}^0}$ (2),…,$\overline{x_{i}^0}$ (n)},$\overline{X_{j}^0}$ ={$\overline{x_{j}^0}$ (1),$\overline{x_{j}^0}$ (2),…,$\overline{x_{j}^0}$ (n)}分别为Xi与Xj的均值零化像,令$\overline{x_{i}^0}$ (li)=$\max\limits _{1 \leqslant k \leqslant n}\left|\left\{\overline{x_{i}^{0}}(k)\right\}\right|, \overline{x_{j}^{0}}\left(l_{j}\right)=\max\limits _{1 \leqslant k \leqslant n}\left|\left\{\overline{x_{j}^{0}}(k)\right\}\right|$ ,则定理3 设Xi与Xj的长度、时距相同且皆为等时距序列,则
证 不妨设Xi与Xj皆为1时距序列,由引理1和定义1得
-
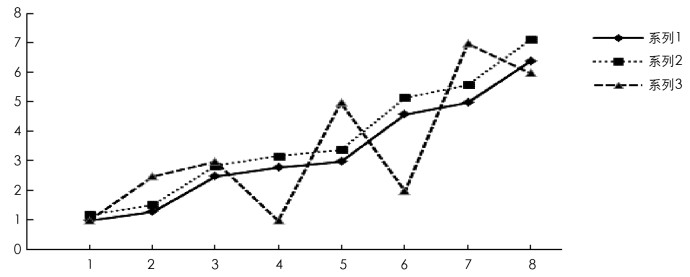
例1 由文献[4],设有如下数据序列:
其中:X1为参考序列,X2与X3为相关因素序列. 计算得到的关联度及其关联序见表 1,数据序列折线图见图 2.
由图 2可以看出,序列X1和X2的发展趋势更接近,而序列X1和X3的发展趋势差异较大,即ε13<ε12. 所以,本文构造的灰色关联度如实地反映了数据序列发展态势的相似程度.
例2 引用文献[5]数据(表 2)对我国海洋渔业经济增长与其影响因素的关系进行研究.
将中国海洋渔业产值作为系统行为的参考序列X0(t),把固定成本、劳动力、自然资源看作X1(k),X2(k),X3(k),k=2001,2007,…,2015.利用本文算子构造的灰色关联模型计算步骤及结果如下:
1) 求均值零化像
$\overline{X_{i}^0}$ (i=0,1,2,3),结果见表 3.2) 求
$\left|\overline{S_{i}}\right|, \left|\overline{S_{i}}-\overline{S_{0}}\right|$ ,i=1,2,3,计算结果如下:3) 由新构造的灰色均值关联度计算公式
得
$\overline{\varepsilon_{01}}$ =0.523 122 53,$\overline{\varepsilon_{02}}$ =0.500 001 272,$\overline{\varepsilon_{03}}$ =0.500 012 733.由计算结果得
$\overline{\varepsilon_{01}}$ >$\overline{\varepsilon_{03}}$ >$\overline{\varepsilon_{02}}$ ,说明对我国海洋渔业经济增长的要素投入关联度影响最大的是固定成本要素,而自然资源和劳动力要素对我国海洋渔业经济影响的关联度差别不大,相对而言,自然资源要素对海洋经济影响略高. 近十年来快速增长的海洋渔业经济使得我国不断增加固定成本投入,同时捕捞船只的修理与维护费用也随着我国捕捞船只数量和功率的增加而增加,在对海水养殖进行投入时,固定成本投入的水平高且贡献率大,因此固定资产投入的增加仍然是当前我国发展海洋渔业经济的重要手段. 均值灰色关联度排在第二的是自然资源要素,“十一五”规划以来,国家“以养为主”政策的实施使得海水养殖不断通过调整养殖结构来适应市场的导向,因此海水养殖的主导地位不断加强,产量的扩大对海洋渔业发展的推动作用也越来越明显. 均值灰色关联度排在第三的是劳动力投入要素. 近年来,由于劳动力数量增长缓慢且劳动生产率不高,相关部门要加大对渔业劳动力转移人群的相关技术培训,积极正确引导渔民的转产转业.本文构造的新的灰色均值关联度模型计算结果跟实际情况相符合,具有一定的实用性和可靠性.
-
针对在利用灰色绝对关联度分析模型做实际问题的定量分析时,存在因自然灾害、战争、疫情等意外因素的影响,引起系统行为序列数据受到冲击干扰而失真的问题,文章根据广义灰色绝对关联分析模型基本思想,采用均值化算子构造方法,提出一种名为均值零化的新关联算子并对灰色绝对关联度模型进行改进. 改进的灰色绝对关联度模型具有规范性、偶对称性、接近性等性质. 初步的数值实例表明,改进的灰色关联度模型能真实地反映序列曲线的关联程度,所得关联分析结果较为客观可靠,新的灰色均值关联度模型算法简单且易于在计算机上实现,具有一定的实用参考价值,从而进一步拓宽了广义灰色关联度模型的应用领域.



 下载:
下载: