考虑到健康肝细胞的一般增长率和细胞-细胞感染方式，建立如下具有病毒DNA核衣壳的HBV感染模型：

其中：T，I，D和V分别代表健康肝细胞、被感染的肝细胞、含有病毒DNA核衣壳和血液中自由病毒颗粒的浓度；健康肝细胞被病毒颗粒感染后以速率β₁成为感染肝细胞，健康肝细胞和被感染细胞接触后以速率β₂被感染；δ表示感染肝细胞的自然死亡率；感染细胞死亡后以速率θ释放出病毒DNA核衣壳；HBV DNA核衣壳以速率δ清除并且以速率α合成新的病毒颗粒；病毒颗粒的自然死亡率是c. 以上所有参数均为正数. f(T)表示健康肝细胞的增长率函数，该函数是光滑且连续的，满足下面的条件

(Ⅰ) ∃T₀>0，使得f(T₀)=0并且f(T)(T-T₀) < 0，T≠T₀.

由条件(Ⅰ)可以得到，对于任意T≠T₀，f′(T) < 0，并且当t→∞时，T(t)→T₀成立. 容易发现，f(T)包含了常数产生和Logistics产生两种方式，更具有普遍性.

引理1  模型(1)具有非负初值的任意解在[0，∞)上是唯一的、非负且一致最终有界的.

证   由文献[11]的相关理论可以直接得到模型(1)的解是唯一存在的. 应用微分方程理论中的常数变易法，得到模型(1)具有非负初值时的解都是非负的. 下面将证明模型的解是一致最终有界的.

由条件(Ⅰ)和模型(1)的第一个方程可以得到，当t≥0并且T≤T₀时，f(T)在[0，T₀]上有界，即存在a和b，使得对于任意的T∈[0，T₀]，有f(T)≤a-bT. 从而有$\frac{\mathrm{d} T(t)}{\mathrm{d} t} \leqslant a-b T $，得到$\lim\limits _{t \rightarrow \infty} \sup T(t) \leqslant \frac{a}{b}$.

定义一个新变量W(t)=T(t)+I(t). 将W(t)关于t求导，得到

其中γ=min{b，δ}.

由常微分的常数变易法，可以得到$ \lim\limits _{t \rightarrow \infty} \sup W(t) \leqslant \frac{a}{\gamma}: =B_W $. 从而，有$ \lim\limits _{t \rightarrow \infty} \sup T(t) \leqslant B_W $，$ \lim\limits _{t \rightarrow \infty} \sup I(t) \leqslant B_W $.将$\lim\limits _{t \rightarrow \infty} \sup I(t) \leqslant B_W $代入到模型(1)的第3个方程，可以得到$ \frac{\mathrm{d} D(t)}{\mathrm{d} t} \leqslant \theta B_W-(\alpha+ \delta) D(t) $. 求解常微分不等式得到$\lim\limits _{t \rightarrow \infty} \sup D(t) \leqslant \frac{\theta B_W}{(\alpha+\delta)}: =B_D $. 由模型(1)的第4个方程，类似可得$ \lim\limits _{t \rightarrow \infty} \sup V(t) \leqslant \frac{\alpha B_D}{c}: =B_V $.

综上所述，可以得到模型的解是一致最终有界的. 证毕.

由引理1，可以得到模型(1)的可行域为

定义模型(1)的基本再生数

其中：R_TV表示一个病毒颗粒在其存活时间内接触健康肝细胞并产生新感染肝细胞的数量，R_TI表示一个感染肝细胞在其存活时间内接触健康肝细胞后产生的新感染细胞的数量.

定理1  模型(1)总是存在一个无病毒感染平衡点E₀=(T₀，0，0，0). 如果R₀>1，除了E₀，模型(1)还存在唯一的病毒感染平衡点E^*.

证   显然，无病毒感染平衡点E₀=(T₀，0，0，0)总是存在. 病毒感染平衡点满足下面的关系式

定义

下面证明存在唯一的T^*使得g(T^*)=1成立. 由于函数g(T)关于T是单调递增且g(0)=0，g(T₀)=R₀. 所以根据连续函数的介值定理，当R₀>1时，存在唯一的T^*∈(0，T₀)，使得g(T^*)=1. 因此当R₀>1时，病毒感染平衡点E^*是存在且唯一的. 证毕.

模型(1)的雅克比矩阵为

定理2  当R₀ < 1时，系统(1)的无病毒感染平衡点E₀是局部渐近稳定的.

证   系统(1)在E₀处的特征方程为

由已知可以得到λ₁=f′(T₀) < 0. 其他三个特征根满足的方程记为λ³+Aλ²+Bλ+C=0，其中$ A=\alpha+ \delta+c+\delta\left(1-\frac{\beta_2 T_0}{\delta}\right) $，$ B=c(\alpha+\delta)+\delta(\alpha+\delta+c)\left(1-\frac{\beta_2 T_0}{\delta}\right) , C=c \delta(\alpha+\delta)\left(1-R_0\right)$. 由R₀的表达式可以得到当R₀ < 1时，$ \frac{\beta_2 T_0}{\delta} < 1$. 从而A，B，C>0. 进一步计算可得AB-C=(δ-β₂T₀)²(α+δ+c)+(α+δ+c)B+αβ₁θT₀>0. 根据Routh-Hurwitz判据得到特征方程(3)的所有根都有负实部，因而E₀是局部渐近稳定的. 证毕.

定理3   当R₀>1时，系统(1)的病毒感染平衡点E^*是局部渐近稳定的.

证  系统(1)在E^*处的特征方程为

其中

由平衡点满足的条件，得到δI^*=β₁T^*V^*+β₂T^*I^*，则有$ \delta=\frac{\beta_1 T^* V^*+\beta_2 T^* I^*}{I^*} $. 故$\delta-\beta_2 T^*=\frac{\beta_1 T^* V^*}{I^*}>0 $. 因此，A_i>0(i=0，1，2，3). 经过计算，可以得到A₀A₁-A₂>0和(A₀A₁-A₂)A₂-A₀²A₃>0. 根据Routh-Hurwitz判据，特征方程(3)的所有根都有负实部，因而E^*是局部渐近稳定. 证毕.

定理4   当R₀ < 1时，系统(1)的无病毒感染平衡点E₀是全局渐近稳定的.

证   定义李雅普诺夫函数如下：

对L(t)沿着系统(1)的解关于时间进行求导，得到

当R₀ < 1时，有$\frac{\mathrm{d} L}{\mathrm{~d} t} \leqslant 0 $，并且{E₀}是$ \left\{(T, I, D, V) \in \varGamma \mid \frac{\mathrm{d} L}{\mathrm{~d} t}=0\right\} $中最大的不变集. 根据Lyapunov-LaSalle不变集原理^[11]，E₀是全局渐近稳定的. 证毕.

定理5   当R₀>1时，系统(1)的病毒感染平衡点E^*是全局渐近稳定的.

证   定义李雅普诺夫函数U(t)如下：

其中

利用关系式f(T^*)=β₁T^*V^*+β₂T^*I^*，对U₁(t)沿着系统(1)的解进行求导，得到

利用关系式δI^*=β₁T^*V^*+β₂T^*I^*，对U₂(t)沿着系统(1)的解进行求导，得到

利用关系式θI^*=(α+δ)D^*，对U₃(t)沿着系统(1)的解进行求导，得到

利用关系式αD^*=cV^*，对U₄(t)沿着系统(1)的解进行求导，得到

结合(5)-(8)式，可以得到

由已知条件f′(T) < 0以及均值不等式，可以得到$ \frac{\mathrm{d} U}{\mathrm{~d} t} \leqslant 0 $. 进一步，当且仅当T=T^*，I=I^*，D=D^*且V=V^*时，不等式严格成立. 从而，{E^*}是$ \left\{(T, I, D, V) \in \varGamma \mid \frac{\mathrm{d} U}{\mathrm{~d} t}=0\right\} $中的最大不变集. 由Lyapunov-LaSalle不变集原理^[11]得知病毒感染平衡点E^*是全局渐近稳定的. 证毕.

本小节将结合MATLAB软件，首先对平衡点的稳定性结果进行数值验证，再比较“细胞-细胞”感染方式引入后对感染细胞和病毒载量的影响. 假设健康肝细胞的增长率函数满足函数f(T)=s-dT，其中s和d分别表示健康肝细胞的自然产生率和衰亡率，参考文献[12]取值如下s=2.6×10⁷，d=0.01. 由文献[13]，模型其他参数取值为：δ=0.053，θ=150，α=0.87，c=3.8. 假设β₂=1.0×10^-12. 各状态变量的初值取值为(6.82×10⁸，2.97×10⁸，6.42×10¹⁰，0.62×10¹⁰).

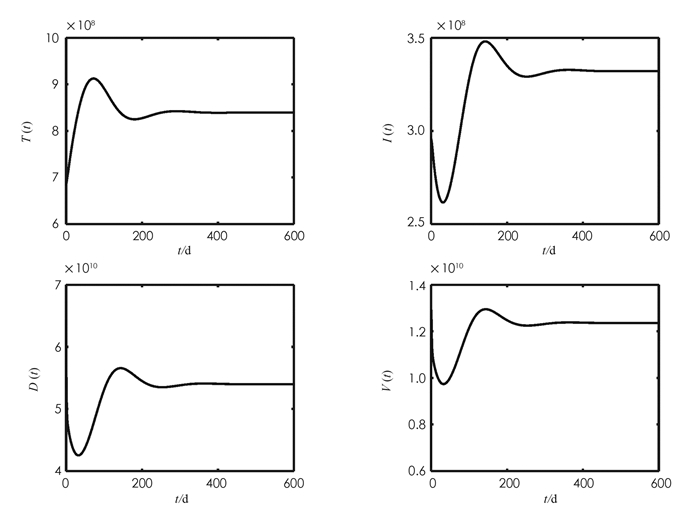
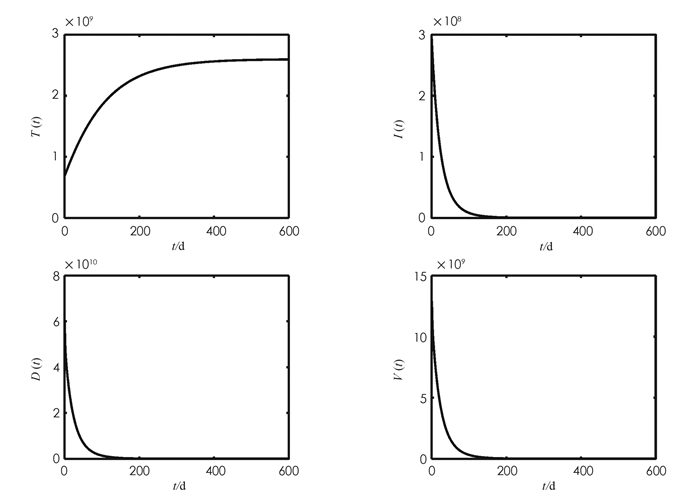
首先通过选取不同的β₁对理论结果进行验证. 参考文献[13]取β₁=3×10^-13，计算得到R₀=0.596 3 < 1. 此时系统(1)仅有一个无病毒感染平衡点E₀=(2.6×10⁹，0，0，0). 由图 1可以观察到系统(1)的各状态变量最终趋向无病毒感染平衡点，即E₀是全局渐近稳定的，验证了定理4的结果. 参考文献[14]取β₁=1.67×10^-12，计算得到R₀=3.053 1>1. 此时系统(1)还存在一个唯一的病毒感染平衡点E^*=(8.516×10⁸，3.298 9×10⁸，5.361 1×10¹⁰，1.227 4×10¹⁰). 图 2显示系统(1)的各状态变量最终趋向病毒感染平衡点，即E^*是全局渐近稳定的，与定理5的结果一致.

现在讨论“细胞-细胞”感染方式对HBV感染细胞和病毒载量的影响. 在图 2参数取值的基础上，假设β₂=0，即不考虑“细胞-细胞”感染，计算得到$\widetilde{R}_0=3.0482 < 3.0531$. 这说明忽略“细胞-细胞”感染，将会低估病毒的传播能力. 进一步数值计算结果显示，此时系统(1)的病毒感染平衡点是E^*=(8.529 7×10⁸，3.296 3×10⁸，5.356 9×10¹⁰，1.226 4×10¹⁰). 比较可得，忽略HBV“细胞-细胞”感染，感染细胞和病毒载量的最终水平分别减少2.55×10⁶和9.5×10⁷，从而低估HBV在人体内的传播水平.

HBV感染人数在我国高居不下，并呈现地方病态势. 为深入研究HBV的感染过程，本文建立了同时考虑病毒DNA核衣壳和“细胞-细胞”感染方式的HBV感染模型，计算了模型的基本再生数和平衡点，通过利用Hurwitz判据和构造Lyapunov函数分别证明了平衡点的局部和全局渐近稳定性，并结合MATLAB数值模拟，对理论结果进行验证. 结果表明“细胞-细胞”感染方式的引入，并没有改变HBV感染的全局稳定性，即病毒总会存在. 但数值计算结果显示，引入“细胞-细胞”感染后，感染细胞和病毒载量的最终水平会升高. 这说明忽略“细胞-细胞”感染，会低估HBV感染细胞和病毒载量的水平，这一结果为HBV病毒感染的临床研究提供了理论支持.