对于q分量混料系统，若试验还受到其他约束条件的限制，我们将试验域记作

其中：φ_j(x)是关于x∈S^q－1的已知函数；a_j，b_j(j=1，2，…，k)为已知常数. 通常$\mathscr{X}$是S^q－1内部的一个不规则凸几何体.

对于任意的$\boldsymbol{x}=\left(x_1, x_2, \cdots, x_q\right)^{\mathrm{T}} \in S^{q-1} \subset \mathscr{X}$以及一个n点设计

我们给出点到点集的距离定义为

其中d²(x，x_i)=‖x－x_i‖²为欧氏距离的平方.

文献[16]提出了3种度量混料试验域设计的均匀性指标，即偏差的定义. 为方便讨论，我们主要讨论均方误偏差和最大距离偏差.

1) 均方误偏差

2) 最大距离偏差

以上两种偏差的计算较为复杂，在实际情形下一般都是采用Monte Carlo方法来计算近似值. 首先生成试验域内的随机混料点集，或使用高阶格子点集

令$\mathscr{L}_{\mathscr{X}}=\mathscr{L}\{q, m\} \cap \mathscr{X}=\left\{\boldsymbol{t}_1, \boldsymbol{t}_2, \cdots, \boldsymbol{t}_{ N }\right\}$作为度量均匀性的NT-net，再令

使用$ {msed}\left(\mathscr{P}_n\right)$和$m d\left(\mathscr{P}_n\right)$分别作为$ {MSED}\left(\mathscr{P}_n\right)$和$M D\left(\mathscr{P}_n\right)$的近似值. 在实际计算中，一般要求N>1 000.

q-1维空间中的正交格子点集可以表示为

其中：$\alpha_{j 1}, \alpha_{j 2}, \cdots, \alpha_{j, q-1} \in \mathbb{Z}; \boldsymbol{e}_{q-1}(i)$为q-1维向量，其第i个元素为1，其余元素为0；c是已知的正数，它表示正交格点之间的距离. 我们记由(2)式生成的正交格子点集为

对于任意的$\boldsymbol{y} \in \mathscr{H}(q-1, c)$，定义y₀的voronoi单元为

这样，我们可以考虑将超立方体内的试验点集转化到单纯形中，并且保持格点之间的距离不变.

为了实现将q-1维超立方体内的正交格子点集变换到单纯形中，我们构造一种线性变换，将$ \mathbb{R}^{q-1} $中的点变换到S^q－1中，且点与点之间的距离保持不变. 文献[17]的单纯形保距独立变换方法如下：

定义一个q-1阶矩阵

其中：$\boldsymbol{w}_1=(\sqrt{2}, 0, \cdots, 0)^{\mathrm{T}}, \boldsymbol{w}_i=\frac{1}{i} \sum\limits_{j=1}^{i-1} \boldsymbol{w}_j+\boldsymbol{e}_{q-1}(i) \sqrt{1+\frac{1}{i}}, i=2, 3, \cdots, q-1$.

记I_q-1为q-1阶单位矩阵，1_q-1为元素全为1的q-1维列向量，J_q－1=1_q-11_q－1^T，易知，(3)式中的矩阵W具有以下性质：

对于W的任意两列w_i，w_j，i≠j，有

W的行列式$\operatorname{det}(\boldsymbol{W})=\sqrt{q}$.

这种变换可以将单纯形S^q－1中的点映射到$\mathbb{R}^{q-1}$中.

例如，对于任意的x∈S^q－1，记x_－i=(x₁，…，x_i－1，x_i+1，…，x_q)^T，则线性变换后的点y=Wx_－i∈$\mathbb{R}$^q－1. 反之，对于任意的$\boldsymbol{y} \in \mathbb{R}^{q-1}$，令x_－i=W^－1y，再令x_i=1－x_－i^T1_q-1，这样得到的点x=(x₁，x₂，…，x_q)^T是位于平面$\sum\limits_{i=1}^q x_i=1$上的点，经过筛选可得到落入S^q－1中的正交格子点集.

对于任意的x_i=(x_i1，x_i2，…，x_iq)^T∈S^q－1，记x_－1，i=(x_i2，x_i3，…，x_iq)^T，即y_i=Wx_－1，i，i=1，2，有‖y₁－y₂‖=‖x₁－x₂‖恒成立.

这是因为由矩阵W的性质可知

由此可见，经过变换后任意两点在$\mathbb{R}^{q-1}$中的距离与S^q－1中是一致的.

我们按照以下方式生成S^q－1中的正交格点.

首先生成$\mathbb{R}^{q-1}$中的正交格子点集$\left\{\boldsymbol{y}_1, \boldsymbol{y}_2, \cdots, \boldsymbol{y}_N\right\} \subset \mathscr{H}\{q-1, c\}$，在混料试验域中选择一点$\boldsymbol{x}_0=\left(x_{01}, x_{02}, \cdots, x_{0 q}\right)^{\mathrm{T}} \in \mathscr{X} $作为参照点，令y₀=Wx_－1，0，其中

其次，令矩阵

是以y₀作为原点而形成的正交格子点集.

最后，进行线性变换，令矩阵

其中$\boldsymbol{X}_{-1}^{\mathrm{T}}=\boldsymbol{W}^{-1} \boldsymbol{Y}^{\mathrm{T}}$. 将X中的点进行筛选，记$\mathscr{H}^{\prime}\{q-1, c\}=\left\{\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_{N}\right\}$是由$\mathscr{H}\{q-1, c\}$经过逆变换而得的试验点集，令

表示最终确定落入试验域内的正交格子点集.

将一个超立方体[a₁，b₁]×[a₂，b₂]×…×[a_q， b_q]记为$H_0=\prod\limits_{i=1}^q\left[a_i, b_i\right]$，该超立方体的顶点集构成的矩阵可表示为

则有以下定理.

定理1   在超立方体$H_0=\prod\limits_{i=1}^q\left[a_i, b_i\right]$上的顶点设计为$\mathscr{P}=\left\{\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_{2^q}\right\}$，c=b_i－a_i，i=1，2，…，q，则

证   首先证明对于任意点x₀=(x₀₁，x₀₂，…，x_0q)^T∈H₀，有

特别地，若$x_0 \in \mathscr{P}$，则$\int_{H_0} d^2\left(\boldsymbol{x}, \boldsymbol{x}_0\right) \mathrm{d} \boldsymbol{x}=\frac{1}{3} q c^{q+2}$. 考虑将H₀每一维的区间二等分，记

其中$\left[a_{i j}, b_{i j}\right]=\left[a_i, a_i+\frac{c}{2}\right]$或$\left[a_{i j}, b_{i j}\right]=\left[a_i+\frac{c}{2}, b_i\right]$. 这样一共可以剖分为2^q个子立方体. 所以有

$\max\limits _{x \in H_0} d^2(\boldsymbol{x}, \mathscr{P})$恰好是立方体中心$\left(a_1, a_2, \cdots, a_q\right)^{\mathrm{T}}+\frac{c}{2} {\bf{1}}_q$到某个顶点的距离，即有$M D(\mathscr{P})=\frac{q c^2}{4}$.

为了使得试验域$\mathscr{X}$内的正交格子点集具有良好的均匀性，即使得设计

的均方误偏差$ {MSED}\left(\mathscr{P}_n\right)$与最大距离偏差$M D\left(\mathscr{P}_n\right)$尽可能地小，我们考虑从以下两个方面来实现.

在$\mathscr{X}$中实施旋转变换，使得落入$\mathscr{X}$内的正交格点尽可能地多. 我们令q-1阶方阵为

其中E_i=e_q－1(i)cosθ_ij－e_q－1(j)sinθ_ij，E_j=e_q－1(j)sinθ_ij+e_q－1(j)cosθ_ij. 在(4)式的基础上，再令

其中Θ=(θ₁₂，θ₁₃，…，θ_{(q－2)(q－1)})为旋转参数向量. 将Y(Θ)经过(5)式的逆变换后得

令$\mathscr{H}_{\mathscr{X}}=\left\{\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_{N}\right\} \cap \mathscr{X}$表示最终确定落入试验域内的正交格子点集. 通过调整(7)式中的参数Θ，使得$\mathscr{H}_{\mathscr{X}}$达到满足要求的均匀性.

$\mathscr{X}$内生成的正交格子点集为$\mathscr{P}_n=\left\{\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_n\right\}$，我们采用在$\mathscr{X} \backslash \left\{\bigcup\limits_{i=1}^n \operatorname{Vor}\left(\boldsymbol{x}_i\right)\right\}$中部分添加若干个试验点的方式，使得最后所得设计的均方误偏差或最大距离偏差尽可能地小.

首先，在$\mathscr{X}$内使用高阶混料格子点集

作为在$\mathscr{X}$上度量一个设计所使用的NT-net. 令

然后使用文献[18]中使用的随机搜索算法，令矩阵$\boldsymbol{R}=\left\{r_{i j}\right\}_{i, j=1}^{N, q}$，其中

这里u_ij(i=1，2，…，N；j=1，2，…，q)相互独立，且都服从均匀分布u_ij~U(0，1).

使用文献[19]的拟分量变换方法，选择适当的拟分量变换参数λ>0，令

其中z_i^(j)=(z_i1^(j)， z_i2^(j)，…，z_iq^(j))^T，令$\boldsymbol{z}_{n+1}^{(j+1)}=\arg \min\limits _{1 \leqslant i \leqslant N_1} {msed}\left\{\mathscr{P}_n, \boldsymbol{z}_i^{(j)}\right\}$. 经过若干轮迭代，最终确定x_n+1使得

以此类推，按照上述方法在$\mathscr{X} \backslash\left\{\bigcup\limits_{i=1}^{n+1} \operatorname{Vor}\left(\boldsymbol{x}_i\right)\right\}$中再添加点x_n+2，最终得到一个设计

如果一个voronoi单元的对角线长度为d，按照添加点的方法构造的设计能使得$M D\left(\mathscr{P}_{n+k}\right)=\frac{d}{2}$.

考虑在试验域$\mathscr{X}$上使用正交格子点集来建模，按(7)式或(8)式生成$\mathscr{X}$上的正交格子点集记为$\mathscr{P}_N=\left\{\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_N\right\}$. 定义高斯核函数为

其中h为已知的窗宽参数，若试验在各点处的观测值为y₁，y₂，…，y_N，则基于正交格点的非参数回归模型为

如果在试验域内有足够多的格点，选择适合的窗宽，能使得非参数回归模型具有很好的预测效果.

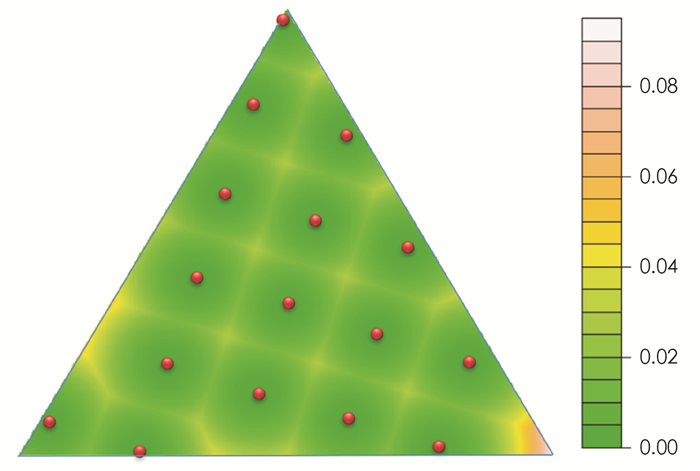
例1  在S^3－1上构造一个正交格点设计，使得各相邻点之间的距离为0.2，通过旋转过后设计点的分布以及试验域内各个点到该设计的距离等高线图如图 1所示.

以模型

为例，在S^3－1上的曲面图如图 2(a)所示，使用正交格点建立非参数回归模型，拟合回归曲面如图 2(b)所示.

由图 2可见，使用正交格点设计建立的非参数回归模型具有很好的稳健性，拟合效果还是不错的.

使用正交格点构造的混料试验域内的设计分布均匀，利于非参数建模，使用文献[20]的方法，结合正交格子点集能有效检验设计的最优性，关于这方面的性质有待进一步研究.