为了更加贴合实际商业模型，假设每个项集包含3个物品. 对于项集中的物品，若仅购买一个物品，则物品质量乘d_3i－2；若购买两个物品，则对两个物品质量之和乘d_3i－1；若项集中物品均被购买，则对其质量之和乘d_3i. 折扣系数满足：

为便于讨论，记

记问题的决策变量为X=[x₁，x₂，…，x_3n]∈{0，1}³ⁿ. 将决策变量中已选择的物品记为集合K. 对于∀i∈N，若

则i∈K，且K_j={i|i∈K，3j－2≤i≤3j}.

将项集中物品所有选择情况记为矩阵A. 则

定义1^[9]  假设问题包含n个项集，每个项集3个物品，则共包含3n个物品，每个项集对应的3个物品的价值系数为P=[P₁，P₂，…，P_n]，质量系数为W=[W₁，W₂，…，W_n]，每个项集对应的折扣率为D=[D₁，D₂，…，D_n]. 其中，P_i=[p_3i－2，p_3i－1，p_3i]，W_i=[w_3i－2，w_3i－1，w_3i]，D_i=[d_3i－2，d_3i－1，d_3i].

给定背包的最大载重为C，为了避免所有解均为可行解，因此

则ESD{0-1}KP模型可描述如下：

决策变量x_i(1≤i≤3n)表示第i个物品是否被装入背包. 式(7)表示目标函数，即满足约束条件下获得收益最大. 式(8)通过先求解第j个项集中物品经过折扣之后的值，再对所有项集的值进行求和. 式(9)表示0-1约束.

与D{0-1}KP类似，ESD{0-1}KP通过在项集中增加物品以表示项集中多个物品同时被选择的情况. 因此，对于n个项集，且每个项集中有且仅有3个物品而言，一共有(2³－1)n=7n种情况存在物品被选择. 记所有的物品选择情况为矩阵R_7n，3n={r_ij}_7n，3n，且有

R_i(1≤i≤7n)表示矩阵R的第i行，则第i行选择情况的价值密度为

将物品序号按照计算完成后的价值密度从高到低的顺序存储在向量H中. 也即对于∀1≤i < j≤7ⁿ，必然有e_Hi≥e_Hj.

结合公式(10)，(11)以及文献[9]提出GSOR，算法伪代码描述见算法1.

算法1  GSOR

输入：X

输出：X

1. T₁=X×P^T；T₂=0

2. FOR i=1：n

3.    $T_2=T_2+\sum\limits_{j=3 i-2}^{3 i} x_j w_j d_{3 i-3+} \sum\limits_{j=3 i-2}^{3 i} x_j$

4. END

5. FOR i=1：7n

6.    X′=sgn(X+R_Hi)

7.    T₃=X′×P^T；T₄=0

8.    FOR j=1：n

9.    $T_4=T_4+\sum\limits_{k=3 j-2}^{3 j} x_k w_k d_{3 j-3+} \sum\limits_{k=3 j-2}^{3 j} x_k$

10.    END

11.    IF T₄≤C

12.        IF T₃>T₂

13.        X=X′

14.        END

15.    END

16.END

在算法GSOR中，步1计算原有决策变量的质量，时间复杂度为O(n). 步2-4计算决策变量的质量，时间复杂度为O(n). 步5-16进行GSOR贪心操作，时间复杂度为O(n²). 其中，步6计算价值密度，步7计算贪心选择的新决策变量的价值，步8-10计算新决策变量的质量，步11-15选择满足约束且价值更大的决策变量进行迭代. GSOR总的时间复杂度为O(n²).

当同一项集中两种选择情况冲突时，GSOR直接对两种物品选择情况取并集.

针对MCKP同一项集中多个物品同时被选择的常见情况，IPA算法有非常良好的求解性能，且理论证明完善. 与ESD{0-1}KP中“每个项集中至多选择一项物品”约束不同，MCKP的约束为“每个项集中选择且仅选择一项物品”. 显然直接使用IPA并不可行，需要建立ESD{0-1}KP与MCKP的等价关系，再将IPA引入到ESD{0-1}KP的求解算法中，达到改进算法的目的.

为便于表述GSOR，将定义1中的ESD{0-1}KP模型转化为传统的D{0-1}KP模型，模型可表述为

其中：

针对D{0-1}KP模型，每个项集中增加一个虚拟物品，其质量与价值均为0，价值密度为0. 则模型可进一步转化如下：

显然，公式(20)要求在每个项集中选择且仅选择一个方案，这类约束为多选择约束. 此时问题为MCKP模型，则使用IPA对同一项集中多个物体同时被选择的情况进行求解. 下面证明ESD{0-1}KP模型与MCKP模型等价.

值得注意的是，MCKP作为一个经典的NP问题，若项集中的物品价值与质量均相同，则问题退化为KP，因此，在MCKP的假设中任意项集不存在两个物品的价值和质量均相等.

定理1  若Y₁满足f₁，g₁，h₁约束，Y₂满足f₂，g₂，h₂约束. 则Y₁与Y₂必然一一对应.

证  对于Y₁=[y₁₁，y₁₂，…，y_1，7n]，新增序号7n+1到8n共计n个物品，其物品价值与质量均为0，则有

因此，对于∀Y₁，必然存在Y₂，使得

下证唯一性，利用反证法，假设∃Y₂≠Y₃，且

显然，若h₁^－1○h₂(Y₂)=h₁^－1○h₂(Y₃)，则必然存在某一项集中有两个质量与价值相等的物品，与假设不符. 故原命题成立.

综上，结论成立.

MCKP的相关内容可参考文献[10-14].

通过增加一个虚拟物品使得ESD{0-1}KP和MCKP在数学模型上完全一致，即传统意义上求解MCKP的算法都能够通过类似增加虚拟物品的操作，对ESD{0-1}KP和D{0-1}KP进行求解，丰富了ESD{0-1}KP和D{0-1}KP求解算法.

从定理1中不难发现，ESD{0-1}KP与MCKP是完全等价的，因此，对于求解MCKP问题的优秀算法也可以用于求解ESD{0-1}KP.

ESD{0-1}KP可采用MCKP的贪心策略进行处理. 同时，公式(18)-(21)模型仍存在传统D{0-1}KP模型缺陷，即非正常个体编码较多，可将MCKP中的贪心策略应用到ESD{0-1}KP模型中.

因IPA拥有计算速度快、求解精度高和算法结构简单等特点，因此基于IPA提出适用于ESD{0-1}KP的NGSOR.

记第i个项集的所有物品为N_i，个数为n. 第i个项集中所有的线性非支配(linear programming undominated，LP-undominated)物品集合称线性非支配子集，并记为L_i. 由文献[15]可知：

定理2^[10]  对于∀s，t∈N_i，w_is>w_ir，w_it>w_ir，p_it>p_ir，若e_it>e_is，且p_it≥p_is，则s∉L_i.

在式(18)-(21)模型中，结合定理2可知，w_is>w_ir=0，w_it>w_ir=0，p_it>p_ir=0. 对于同一项集中两个物品s，t同时被选择时，若e_it>e_is，且p_it≥p_is，则选择物品t而不选择物品s.

即对于ESD{0-1}KP，当按照选择方案的价值密度从高到低选择时，若同一项集中两个选择方案同时被选择，应当选择价值更大的选择方案. 由此得到NGSOR算法，算法伪代码如下：

算法2  NGSOR

输入：X

输出：X

1. FOR i=1：n

2. P_s=[p_3i－2，p_3i－1，p_3i－2+p_3i－1，p_3i，p_3i－2+p_3i，p_3i－1+p_3i，p_3i－2+p_3i－1+p_3i]

3. W_s=[d_3i－2w_3i－2，d_3i－2w_3i－1，d_3i－1(w_3i－2+w_3i－1)，d_3i－2w_3i，d_3i－1(w_3i－2+w_3i)，d_3i－1(w_3i－1+w_3i)，d_3i－2(w_3i－2+w_3i－1+w_3i)]

4. P′=[P′，P_s]；W′=[W′，W_s]

5. END

6. E=P′. /W′；E=[E；1：7n]

7. E=－sortrows(－E′，1)′；H=E₂

8. X=zeros(1，n)

9. FOR i=1：7n

10. $t_1=\left\lfloor\frac{\boldsymbol{H}_i-1}{7}\right\rfloor+1$

11. t₂=X_{3t1－2：3t1}×P^T_{3t1－2：3t1}

12. IF t₂=0

13.     e₁=0

14. ELSE

15. t₃=w′_{X3t1－2：3t1×[1, 2, 4]′+3t1－3}；e₁=t₂/t₃

16. END

17. t₄=p′_Hi；t₅=w′_Hi；e₂=t₄/t₅

18. T=X；T_{3t1－2：3t1}=A_Hi－7t1+7；Q=0

19. FOR j=1：n

20.     IF sum(T_3j－2：3j)>0

21.     Q=Q+w′_{T3j－2：3j×[1, 2, 4]′+7j－7}

22.     END

23. END

24. IF Q≤C

25.     IFt₂ < t₄

26.         X=T

27.     END

28. END

29. END

NGSOR与GSOR在时间复杂度上无数量级差异，但在GSOR中的步3与步9都需要重新计算每个项集选择情况所对应的质量，而在NGSOR中则通过存储后直接调用，因此NGSOR算法求解速度更快.

为充分展示NGSOR的算法性能，不仅与现有GSOR进行对比，同时与将文献[9]贪心遗传算法(greedy genetic algorithm，GGA)中的GSOR替换成NGSOR后得到的新型贪心遗传算法(new greedy genetic algorithm，NGGA)进行对比. 关于遗传算法的相关内容可参考文献[16-18].

因NGGA仅将GGA中的贪心策略进行了修改，因此沿用文献[9]中的参数算法设种群为50，最大迭代次数为100次，交叉概率p_c=0.8，变异概率p_m=0.01. 此外，ESD{0-1}KP中，折扣系数为d_3i－2=1，d_3i－1=0.8，d_3i=0.7.

测试数据集沿用文献[9]中4类大规模实例，具体测试数据参数可参考文献[9]. 其中，数据规模为300≤n≤3 000，且

1) EUDKP1-EUDKP10，参数设置w_j∈_z[2，1 000]，p_j∈_z[2，1 000].

2) EWDKP1-EWDKP10，参数设置w_j∈_z[101，1 000]，p_j∈_z[w_j－100，w_j+100].

3) ESDKP1-ESDKP10，参数设置w_j∈_z[2，1 000]，p_j∈w_j+100.

4) EIDKP1-EIDKP10，参数设置p_j∈_z[2，1 000]，w_j∈p_j+100.

其中_z[a，b]表示在整数a到整数b之间的整数集.

文章使用计算机基本配置为：Intel Core i7-8700 CPU@3.2GHz(12核)，16GB DDR4L，Microsoft Windows 10家庭版. 利用MATLAB R2016a对问题进行求解及绘图.

利用NGSOR，GSOR，GGA和NGGA对4类数据进行求解. 因NGSOR和GSOR算法为非随机算法，因此仅参考最优值和求解时长指标. 对于GGA和NGGA，因其为随机算法，因此除了最优值和求解时长以外，还需要增加平均值和最差值指标.

为避免单次计算的偶然因素干扰，所有算法的求解时长为30次独立求解均值. 同时，为检验NGSOR的算法效果，对GGA重新进行测试.

算法计算结果见表 1，其中折扣背包问题的动态规划算法(dynamic programming of discounted knapsack problem，DPDKP)计算得到的结果为精确解.

由表 1知，基于EUDKP算例，相比于GSOR的算法精度，NGSOR的误差范围从40.23%~50.54%缩小至3.97%~6.09%，对所有算例的提升精确度进行平均计算得到算法精度平均提升41.42%，同理得到算法速度平均提升40.68%. 应用到遗传算法中，NGGA相比于GGA，最优解精度平均提升33.22%，平均值精度平均提升34.42%.

基于EWDKP算例，相比于GSOR的算法精度，NGSOR的误差范围从10.32%~35.04%缩小至0.01%~0.22%，算法精度平均提升19.82%，同时算法速度平均提升45.85%. 应用到遗传算法中，NGGA相比于GGA，最优解精度平均提升15.18%，平均值精度平均提升16.07%.

基于ESDKP算例，相比于GSOR的算法精度，NGSOR的误差范围从12.98%~17.55%缩小至0.12%~0.41%，算法精度平均提升15.07%，同时算法速度平均提升44.31%. 应用到遗传算法中，NGGA相比于GGA，最优解精度平均提升15.08%，平均值精度平均提升15.07%.

基于EIDKP算例，相比于GSOR的算法精度，NGSOR的误差范围从18.70%~29.38%缩小至0.00%~0.06%，算法精度平均提升21.97%，同时算法速度平均提升48.94%. 应用到遗传算法中，NGGA相比于GGA，最优解精度平均提升14.56%，平均值精度平均提升15.96%.

整体分析，就算法精度讨论，NGSOR平均误差为1.31%，GSOR平均误差为25.87%，平均提升24.56%. 就算法速度而言，平均提升44.95%. 总体上，NGSOR相对于GSOR具有明显优势，更加适应用于ESD{0-1}KP的求解，效果理想.

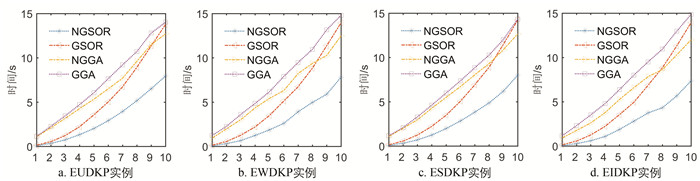
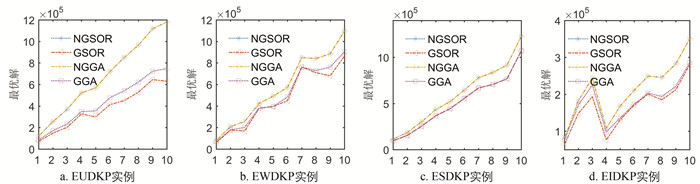
为了更好展示NGSOR性能，将表 1数据绘制成图 1与图 2. 从图 1中不难发现，NGSOR与NGGA求解效果均比GSOR和GGA效果更好. 从图 2中可以知道，在求解时长方面，NGGA比GGA更快，且NGSOR也比GSOR更快.

文章基于GSOR，通过改进模型，将ESD{0-1}KP与D{0-1}KP转化为MCKP，再引入IPA对问题进行处理，算法性能提升明显. 值得注意的是，当ESD{0-1}KP的项集中物品数量继续增加时，无论是NGSOR还是GSOR都需要指数级储存空间，NGSOR虽然能够提供更好的贪心结果，但其内存需求与GSOR并无特别大的改进. 下一步工作，不妨思考新的支配关系与剪枝策略，提出更加优秀的贪心算法.