决策粗糙集模型由2种状态和3种行动构成^[2]. 设状态集$ X=\{C,\rightharpoondown C\}$，表示对象属于C和$ \rightharpoondown C$两种状态. 行动集记为A={a_P，a_B，a_N}，其中a_P，a_B和a_N分别表示对象属于接受决策、延迟决策和拒绝决策的3种行动，即：x∈POS(C)、x∈BND(C)和x∈NEG(C). 这3种行动在2种状态下对应的损失可采用3×2矩阵表示，具体见表 1.

表 1中λ_PP，λ_BP和λ_NP表示对象属于状态C时，采取a_P，a_B和a_N3种行动的代价损失. 类似地，当λ_PN，λ_BN和λ_NN表示对象不属于状态C时，分别采取3种行动对应的损失. 设Pr(C|[x])为对象x隶属于状态C的条件概率，对象x通常用等价类[x]表示，则对象x的决策代价损失函数R(a_*|[x])(*=P，B，N)的计算公式为：

根据贝叶斯最小风险决策理论，可得以下决策规则^[2]：

上述规则P-N称之为三支决策^[2-3]. 基于$ \operatorname{Pr}(C \mid[x])+\operatorname{Pr}(\rightharpoondown C \mid[x])=1$，规则P-N通常考虑如下合理情形：

进一步可简化为规则P1-N1：

其中α，β和γ可表达为：

其中：阈值α，β和γ满足0≤α≤1、0≤β≤1且0≤γ≤1. 此外，从规则B1中可知，阈值α和β存在两种情形：(Ⅰ) α>β和(Ⅱ)α≤β.

(Ⅰ) α>β，满足：(λ_PN-λ_BN)(λ_NP-λ_BP)>(λ_BP-λ_PP)(λ_BN-λ_NN)可得α>γ>β，此时规则P1-N1进一步简化为：

P2 当Pr(C|[x])≥α时，x∈POS(C)；

B2 当β <Pr(C|[x]) <α时，x∈BND(C)；

N2 当Pr(C|[x])≤β时，x∈NEG(C).

(Ⅱ) 当α≤β，满足：(λ_PN-λ_BN)(λ_NP-λ_BP)>(λ_BP-λ_PP)(λ_BN-λ_NN). 此时规则P1-N1简化为二支决策如下：

P3 如果Pr(C|[x])≥γ，x∈POS(C)；

N3 如果Pr(C|[x]) < γ时，x∈NEG(C).

在介绍语言直觉模糊数之前，首先给出直觉模糊数的定义^[26].

定义1    设U={x₁，x₂，…，x_n}为某非空论域. 则U上的直觉模糊集F定义为：

其中：μ_F(x)∈[0, 1]和ν_F(x)∈[0, 1]分别表示x属于模糊集F的隶属度和非隶属度. 对于x∈U，满足μ_F(x)+ν_F(x)∈[0, 1]. 特别地，γ =(μ，ν)被称为直觉模糊数(intuitionistic fuzzy number，IFN) ^[15].

基于直觉模糊数的概念，给出语言直觉模糊数的定义^[27].

定义2   设S={s_i|i=0，1，2，…，g}和$\widetilde{S}=\left\{s_i \mid i \in[0, g]\right\} $分别为离散和连续的语言术语集. 如果s_u，s_v∈$ \widetilde{S}$且u+v≤g，那么γ=(s_u，s_v)称之为语言直觉模糊数. 特别地，若s_u，s_v∈S，则γ=(s_u，s_v)为原始语言直觉模糊数. 否则，为虚拟语言直觉模糊数.

考虑到语言直觉模糊数在刻画不确定损失函数方面相比于其他评价更灵活, 且更符合人类自然语言的表达. 为此，本研究采用语言直觉模糊数来评价损失函数，进而形成语言直觉模糊三支群决策问题，该问题包括$\Omega=\{C, \rightharpoondown C\} \underline{\underline \Delta } \{P, N\} $ 2种状态和A={a_P，a_B，a_N}3种行动. 专家在2种状态$ \circ $($ \circ $ =P，N)下采取3种行动a_*(*=P，B，N)将会产生相应的6种损失：λ_PP，λ_BP，λ_NP，λ_NN，λ_BN和λ_PN. 邀请n(n≥2)位专家针对m个对象分别给出语言直觉模糊损失评价. 设E={e₁，e₂，…，e_n}是由n个专家组成的集合，X={x₁，x₂，…，x_m}是由m个对象组成的集合，W=(ω₁，ω₂，…，ω_n) ^T是专家权重向量，其中$\sum\limits_{k=1}^n \omega_k=1 $且0≤ω_k≤1. 为了获得具有群体共识的综合损失函数与三支决策规则，专家需要提供代价损失函数评价值. 实际中，专家们能基于离散语言术语S={s₀，s₁，…，s_g}采用语言直觉模糊数表达他们的偏好. 设专家e_k给出的代价损失函数评价值为λ_ij=(s_uij^k，s_vij^k)，k=1，2，…，n；i=1，2，…，m；j表示第j个代价损失函数，且j=1，2，…，6. 其中s_uij^k∈S，s_vij^k∈S，0≤u_ij^k+v_ij^k≤g. 专家e_k针对m个对象x_i提出的代价损失函数评价值λ_ij^k构成专家评价矩阵E_k，其中E_k=(λ_ij^k) _m×6为：

为了表达方便，将第k个专家的评价矩阵E_k简记为E_k=(E_k1，E_k2，…，E_ki，…，E_km) ^T，其中E_ki为矩阵E_k中第i个对象对应的6个代价损失函数构成的行向量. 采用最优集成方法将n个专家提供的评价矩阵E_k进行集成，从而获得具有群体共识的综合损失函数评价矩阵E，可表达为：

为了表达方便，专家综合评价矩阵E可类似地表达为E=(E₁，E₂，…，E_i，…，E_m)^T，其中E_i为矩阵E中第i个对象对应的6个代价损失函数构成的行向量.

根据上述问题和表达方式，下面给出语言直觉模糊相似测度，并采用该测度来度量专家个体给出的语言直觉模糊评价矩阵E_k与群体综合评价矩阵E之间的相似性，进而构建群体一致度指标，且采用该指标度量群体的综合一致性水平，进而建立基于语言直觉模糊相似度的最优集成模型.

根据海明距离，首先给出语言直觉模糊损失函数距离的定义.

定义3   设E_ki为第k(k=1，2，…，n)个专家关于第i(i=1，2，…，m)个对象的6个代价损失函数构成的行向量，E_i为n个专家对第i个对象的6个综合代价损失函数构成的行向量，则E_ki与E_i之间的距离测度定义为：

其中f为语言术语集S={s₀，s₁，…，s_g}到实数集R之间的映射. 为了计算方便，假设映射f为f(s_u)=u/g，f(s_v)=v/g.

根据定义3，构建专家个体语言直觉模糊评价矩阵E_k和群体综合评价矩阵E之间的相似测度S(E_k，E).

定义4  设E_k为第k(k=1，2，…，n)个专家e_k给出的语言直觉模糊评价矩阵，E为群体综合评价矩阵. 则E_k与E之间的相似测度S(E_k，E)定义为：

基于定义4，构建群体一致度指标GCI.

定义5  设S(E_k，E)为专家e_k给出的语言直觉模糊评价矩阵E_k和群体综合评价矩阵E之间的相似测度，则由n个专家构成的群体一致度指标GCI定义为：

根据Lee^[28]的研究成果，建立基于第k个专家给出的语言直觉模糊评价矩阵E_k与群体综合评价矩阵E之间非相似度最小的最优集成模型. 具体为：

其中t>1为整数且c>1是常数.

根据模型(1)，可得命题1^[28].

命题1   当专家权重ω_k(k=1，2，…，n)和群体综合评价矩阵E满足下列关系时，模型(1)达到局部最小值.

基于命题1，设计一种实现语言直觉模糊综合损失函数一致性的迭代算法，并证明该算法的收敛性.

算法1：基于最优集成模型的综合损失函数一致性实现算法

输入：专家e_k的个体评价矩阵E_k(k=1，2，…，n)

输出：具有群体共识的综合损失函数矩阵E

随机生成$ \boldsymbol{W}=\left(\omega_1, \omega_2, \cdots, \omega_n\right)^{\mathrm{T}}$，其中0≤ω_k≤1且$\sum\limits_{k=1}^n \omega_k=1 $.

$\boldsymbol{W}^{(0)}=\boldsymbol{W}$,

$r=0$,

$\boldsymbol{E}^{(0)}=L I F W A_{W(0)}\left(\boldsymbol{E}_k\right)=\sum\limits_{k=1}^n \omega_k^{(0)} \boldsymbol{E}_k$,

$G C I^{(0)}=\frac{1}{n} \sum\limits_{k=1}^n S\left(\boldsymbol{E}_k, \boldsymbol{E}^{(0)}\right)$.

while $r \geqslant 0$

$\quad \omega_k^{(r+1)}=\frac{\left(1 /\left(c-S\left(\boldsymbol{E}_k, \boldsymbol{E}^{(r)}\right)\right)\right)^{1 /(t-1)}}{\sum\limits_{l=1}^n\left(1 /\left(c-S\left(\boldsymbol{E}_l, \boldsymbol{E}^{(r)}\right)\right)\right)^{1 /(t-1)}}$

计算$\boldsymbol{E}^{(r+1)}=L I F W A_{W(r+1)}\left(\boldsymbol{E}_k\right)=\sum\limits_{k=1}^n \omega_k^{(r+1)} \boldsymbol{E}_k$

计算$G C I^{(r+1)}=\frac{1}{n} \sum\limits_{k=1}^n S\left(\boldsymbol{E}_k, \boldsymbol{E}^{(r+1)}\right)$

if $\left|G C I^{(r+1)}-G C I^{(r)}\right| \leqslant \varepsilon$

输出E^(r+1)

Break

else

r=r+1

end

end

Return E^(r+1)

为了证明上述算法的收敛性，首先给出命题2.

命题2   设f(x)是可导函数且f′(x)在闭区间[c，d]上有界. 则f(x)在[c，d]上是一致连续的，即对于任意x，y∈[c，d]满足|x-y| < ε，则|f(x)-f(y)| < ε′，其中ε和ε′均为无穷小量，ε>0且ε′>0.

证   因为f(x)是可导函数，f′(x)在闭区间[c，d]上有界，即存在一个极大的M>0，使得|f′(x)|≤M，并且对于任意x，y∈[a，b]满足|x-y| < ε，则可以得到|f(x)-f(y)|=|f′(ξ)||x-y| < Mε=ε′，其中ξ∈[min x，y，max x，y]$ \subseteq $[c，d]. 因此，f(x)在[c，d]是一致连续的.

根据命题2，可进一步得到命题3.

命题3   设0≤x_k≤1，0≤y_k≤1且0≤a_k≤1，其中k=1，2，…，n. 对于任意k=1，2，…，n，满足|x_k-y_k| <ε，则$\left|\prod_{k=1}^n\left(a_k\right)^{x_k}-\prod_{k=1}^n\left(a_k\right)^{y_k}\right| <\varepsilon^{\prime} $，其中ε>0，ε′>0.

证   对于任意k=1，2，…，n，满足|x_k-y_k|<ε，恒有：

假设a=min{a₁，a₂，…，a_n}和ε′=-naⁿln(a)ε，可得0 <a <1和$-\sum\limits_{k=1}^n \ln \left(a_k\right)\left|x_k-y_k\right| <-n \ln (a) \varepsilon $，因此$ \left|\ln \left(\prod_{k=1}^n\left(a_k\right)^{x_k}\right)-\ln \left(\prod_{k=1}^n\left(a_k\right)^{y_k}\right)\right| <-n \ln (a) \varepsilon$. 根据命题2，可得：

根据命题3，可得命题4.

命题4    若ω_k^(r+1)-ω_k^(r) <ε，则d(E_ki，E_i^(r+1))-d(E_ki，E_i^(r)) <ε′，其中ε>0且ε′>0.

证

令$u_k=1-u_{i j}^k / g, v_k=1-v_{i j}^k / g$. 由命题2和命题3可知，当$\left|\omega_k^{(r+1)}-\omega_k^{(r)}\right| <\varepsilon$时，有$\left|\left(g-g \prod_{k=1}^n\left(1-u_{i j}^k / g\right)^{\omega_k^{(r)}}\right)-\left(g-g \prod_{k=1}^n\left(1-u_{i j}^k / g\right)^{\omega_k^{(r+1)}}\right)\right|=\left|g \prod_{k=1}^n\left(u_k\right)^{\omega_k^{(r)}}-g \prod_{k=1}^n\left(u_k\right)^{\omega_k^{(r+1)}}\right| <$ $g \varepsilon^{\prime}$，且$\left|g \prod_{k=1}^n\left(v_{i j}^k / g\right)^{\omega_k^{(r)}}-g \prod_{k=1}^n\left(v_{i j}^k / g\right)^{\omega_k^{(r+1)}}\right|=\left|g \prod_{k=1}^n\left(v_k\right)^{\omega_k^{(r)}}-g \prod_{k=1}^n\left(v_k\right)^{\omega_k^{(r+1)}}\right| <g \varepsilon^{\prime}$. 因此，当$\left|d\left(E_{k i}, E_i^{(r+1)}\right)-d\left(E_{k i}, E_i^{(r)}\right)\right| <\varepsilon^{\prime \prime} <\varepsilon$，有$\left|f\left(s_{g-g} \prod_{k=1}^n\left(1-u_{i j}^k / g\right)^\omega{ }_k^{(r)}\right)-f\left(s_{g-g} \prod_{k=1}^n\left(1-u_{i j}^k / g\right)^\omega{ }_k^{(r+1)}\right)\right| <\varepsilon^{\prime \prime}$，且$\left|f\left(s_g \prod_{k=1}^n\left(v_{i j}^k / g\right) \omega_k^{(r)}\right)-f\left(s_g \prod_{k=1}^n\left(v_{i j}^k / g\right)^\omega{ }_k^{(r+1)}\right)\right| <\varepsilon^{\prime \prime}$.

因此$\left|d\left(E_{k i}, E_i^{(r+1)}\right)-d\left(E_{k i}, E_i^{(r)}\right)\right| <\varepsilon^{\prime \prime} <\varepsilon$.

根据命题4，容易得到命题5.

命题5    若$\left|\omega_k^{(r+1)}-\omega_k^{(r)}\right| <\varepsilon$，则$\left|\mathrm{GCI}^{(r+1)}-\mathrm{GCI}^{(r)}\right| <\varepsilon$，其中ε>0.

证

由命题4可得，$\frac{1}{m n} \sum\limits_{k=1}^n \sum\limits_{i=1}^m\left|d\left(E_{k i}, E_i^{(r)}\right)-d\left(E_{k i}, E_i^{(r+1)}\right)\right| <\varepsilon$.

综上所述，当$\left|\omega_k^{(r+1)}-\omega_k^{(r)}\right| <\varepsilon$时，$\left|\mathrm{GCI}^{(r+1)}-\mathrm{GCI}^{(r)}\right| <\varepsilon$.

当算法1的迭代终止条件$\left|\mathrm{GCI}^{(r+1)}-\mathrm{GCI}^{(r)}\right| <\varepsilon$替换为$\left\|W^{(r+1)}-W^{(r)}\right\| <\varepsilon$时，该算法可以退化成文献[29]中的算法；而该文献验证了算法的收敛性，并结合命题5可知，上述基于权重迭代的一致性综合损失函数获取算法算法1是收敛的. 因此，采用算法1能获得一致性综合损失函数矩阵E. 为了方便后续讨论，记E为如下：

其中$\boldsymbol{E}_i=\left(\lambda_{\mathrm{PP}}^i, \lambda_{\mathrm{BP}}^i, \lambda_{\mathrm{NP}}^i, \lambda_{\mathrm{NN}}^i, \lambda_{\mathrm{BN}}^i, \lambda_{\mathrm{PN}}^i\right)$和$\lambda_{* \circ}^i=\left(s_{u_*^i}^i, s_{v_*^i}^i\right)\left(*=\mathrm{P}, \mathrm{B}, \mathrm{N}, { }^i=\mathrm{P}, \mathrm{N}\right)$.

根据Liu等^[15]提出的语言直觉模糊三支决策阈值确定模型，下面建立确定语言直觉模糊三支群决策阈值的单一优化模型且首先给出下面命题.

命题6   基于算法1获得的一致性综合损失函数E，可计算第i个对象x_i(i=1，…，m)在行动a_*(*=P，B，N)下的期望损失$\bar{R}\left(a_* \mid\left[x_i\right]\right)$为：

其中$u_*^i=2 g-g\left[\left(1-u_{* P}^i / g\right)^{p_i}+\left(1-u_{* N}^i / g\right)^{q_i}\right]-g\left[1-\left(1-u_{* P}^i / g\right)^{p_i}\right]\left[1-\left(1-u_{* N}^i / g\right)^{q_i}\right]$且$v_*^i=$ $\left(v_{* P}^i\right)^{P_i}\left(v_{* N N}^i\right)^{q_i}$.

根据贝叶斯风险决策理论，获得三支决策规则：

规则P4-N4会涉及到语言直觉模糊排序方法，因此，采用文献[15]中的排序方法对其进行排序. 首先给出命题7^[15].

命题7   为方便表达，记$\bar{R}\left(a * \mid\left[x_i\right]\right)=\left(s_{u_u}, s_{v_{v^{\prime}}}\right)(*=\mathrm{P}, \mathrm{B}, \mathrm{N})$，其中$u_*^i=2 g-g\left[\left(1-\frac{u_{* P}^i}{g}\right)^{p_i}+\left(1-\frac{u_{* N}^i}{g}\right)^{q_i}\right]-g\left[1-\left(1-\frac{u_{* P}^i}{g}\right)^{p_i}\right]\left[1-\left(1-\frac{u^i{ }_{* N}}{g}\right)^{q_i}\right], v_*^i=\left(v^i{ }_{* P}\right)^{p_i}\left(v^i{ }_{* N}\right)^{q_i}$，则$\bar{R}\left(a * \mid\left[x_i\right]\right)$的排序函数$\operatorname{LM}\left(\bar{R}\left(a * \mid\left[x_i\right]\right)\right)$为$L M\left(\bar{R}\left(a * \mid\left[x_i\right]\right)\right)=\frac{1}{g} \sqrt{\left(u_*^i\right)^2+\left(g-v_*^i\right)^2}-$ $\sqrt{\left(g-u_*^i\right)^2+\left(v_*^i\right)^2}+\sqrt{\left(u_*^i\right)^2+\left(v_*^i\right)^2}$.

文献[15]知，排序函数$L M\left(\bar{R}\left(a * \mid\left[x_i\right]\right)\right)$为越大越好型，则规则P4-N4进一步转化为P5-N5：

P5    当$L M\left(\bar{R}\left(a_{\mathrm{P}} \mid\left[x_i\right]\right)\right) \leqslant L M\left(R\left(a_{\mathrm{B}} \mid\left[x_i\right]\right)\right)$且$L M\left(R\left(a_{\mathrm{P}} \mid\left[x_i\right]\right)\right) \leqslant L M\left(R\left(a_{\mathrm{N}} \mid\left[x_i\right]\right)\right)$，则$x_i \in \operatorname{POS}(C) ;$

B5    当$L M\left(\bar{R}\left(a_{\mathrm{B}} \mid\left[x_i\right]\right)\right) \leqslant L M\left(\bar{R}\left(a_{\mathrm{P}} \mid\left[x_i\right]\right)\right)$且$L M\left(R\left(a_{\mathrm{B}} \mid\left[x_i\right]\right)\right) \leqslant L M\left(R\left(a_{\mathrm{N}} \mid\left[x_i\right]\right)\right)$，则$x_i \in \operatorname{BND}(C)$;

N5k    当$\operatorname{LM}\left(\bar{R}\left(a_{\mathrm{N}} \mid\left[x_i\right]\right)\right) \leqslant \operatorname{LM}\left(R\left(a_{\mathrm{P}} \mid\left[x_i\right]\right)\right)$且$L M\left(R\left(a_N \mid\left[x_i\right]\right)\right) \leqslant L M\left(R\left(a_{\mathrm{B}} \mid\left[x_i\right]\right)\right)$，则$x_i \in \operatorname{NEG}(C)$；

基于规则P5-N5，建立语言直觉模糊三支群决策阈值的单一优化模型$\left(\bar{p}_{i 1}^{\text {op }}, \bar{p}_{i 2}^{\text {opt }}\right)$-model. 具体为：

具体可化为：

其中：

$u_{* 1}^i=2 g-g\left[\left(1-\frac{u_{* \mathrm{P}}^i}{g}\right)^{\bar{p}_{i 1}}+\left(1-\frac{u_{* \mathrm{~N}}^i}{g}\right)^{\bar{q}_{i 1}}\right]-g\left[1-\left(1-\frac{u_{* \mathrm{P}}^i}{g}\right)^{\bar{p}_{i 1}}\right]\left[1-\left(1-\frac{u_{* \mathrm{~N}}^i}{g}\right)^{\bar{q}_{i 1}}\right]$且$v_{* 1}^i= \left(v_{* \mathrm{P}}^i\right)^{\bar{p}_{i 1}}\left(v_{* \mathrm{~N}}^i\right)^{\bar{q}_{i 1}} ;$

$u_{* 2}^i=2 g-g\left[\left(1-\frac{u_{* \mathrm{P}}^i}{g}\right)^{\bar{p}_{i 2}}+\left(1-\frac{u_{* \mathrm{~N}}^i}{g}\right)^{\bar{q}_{i 2}}\right]-g\left[1-\left(1-\frac{u_{* \mathrm{P}}^i}{g}\right)^{\bar{p}_{i 2}}\right]\left[1-\left(1-\frac{u_{* \mathrm{~N}}^i}{g}\right)^{\bar{q}_{i 2}}\right] $且$v_{* 2}^i= \left(v_{* \mathrm{P}}^i\right)^{\bar{p}_{i 2}}\left(v_{* \mathrm{~N}}^i\right)^{\bar{q}_{i 2}} \cdot(*=\mathrm{P}, \mathrm{B}, \mathrm{N})$

根据文献[15]，模型(3)的最优解$\left(\bar{p}_{i 1}^{\mathrm{opt}}, \bar{q}_{i 1}^{\mathrm{opt}}, \bar{p}_{i 2}^{\mathrm{opt}}, \bar{q}_{i 2}^{\mathrm{opt}}\right)$是存在且唯一性.

下面给出基于语言直觉模糊数评价的三支群决策方法，具体步骤如下：

步骤1：专家e_k(k=1，2，…，n)针对m个对象x_i(i=1，2，…，m)分别给出语言直觉模糊损失函数评价(s_{u ij}^k，s_{v ij}^k)，进而构造专家语言直觉模糊评价矩阵E_k=((s_{u ij}^k，s_{v ij}^k))_m×6，假定已知每个对象的条件概率Pr(C|[x_i]).

步骤2：给定误差值ε，并设置参数r，m，c，采用算法1来获取满足一致性要求的综合代价损失函数矩阵E=(E₁，E₂，…，E_i，…，E_m)^T，其中E_i=(λ_PPⁱ，λ_BPⁱ，λ_NPⁱ，λ_NNⁱ，λ_BNⁱ，λ_PNⁱ)，其中i=1，2，…，m.

步骤3：基于一致性综合损失函数，建立确定语言直觉模糊三支群决策阈值的单一优化模型.

步骤4：采用MATLAB求解该模型，并得到最优解$\alpha_i=\bar{p}_{i 1}^{\text {opt }}, \beta_i=\bar{p}_{i 2}^{\text {opt }}(i=1,2, \cdots, m) $.

ⅰ) 当α_i>β_i，采用三支决策规则，即：

P6 若Pr(C|[x_i])≥α_i时，x_i∈POS(C)；

B6 当β_i <Pr(C|[x_i]) <α_i时，x_i∈BND(C)；

N6 当Pr(C|[x_i])≤β_i时，x_i∈NEG(C).

ⅱ) 当α_i≤β_i，采用二支决策规则，即：

P7 如果Pr(C|[x_i])≥α_i，x_i∈POS(C)；

N7 如果Pr(C|[x_i]) <β_i，x_i∈NEG(C).

假设某投资人面对3个投资项目X={x₁，x₂，x₃}，现考虑是否投资发展，这些项目根据以往经验分为盈利的项目(C)和亏损的项目($ \rightharpoondown C$). 投资人根据上述项目可以选择投资(a_P)、进一步考虑(a_B)和不投资(a_N)3种决策行动. 为了获得巨大的经济效益，投资人聘请了3位投资学专家来做出科学合理的决策. 设上述3个项目就每个项目选择投资、进一步考虑以及不投资行动后的代价损失函数由专家基于标度S={s₀，s₁，s₂，s₃，s₄，s₅，s₆}给出，具体结果详见表 2-表 4. 基于以上信息，投资人将如何做出投资决策？假定3个投资项目x_i(i=1，2，3)对应的条件概率分别为Pr(C|[x₁])=0.855 5，Pr(C|[x₂])=0.125 0和Pr(C|[x₃])=0.798 0.

步骤1：3个专家e_k(k=1，2，3)针对3个对象x_i(i=1，2，3)分别给出语言直觉模糊损失函数评价(s_uij^k，s_vij^k)，进而构造专家语言直觉模糊评价矩阵E_k=((s_uij^k，s_vij^k))_3×6.

步骤2：给定误差值ε=10^-15，并设置参数r=0，t=3，c=2，采用算法1来获取满足一致性综合代价损失函数矩阵(表 5).

步骤3：基于算法1获取的一致性综合损失函数，建立确定语言直觉模糊三支群决策阈值的单一优化模型($ \tilde{\alpha}_i^{\mathrm{opt}}$，$ \tilde{\beta}_i^{\text {opt }}$)-model，其中i=1，2，3.

步骤4：采用MATLAB求解该模型，并得到三支决策阈值对最优解(表 6).

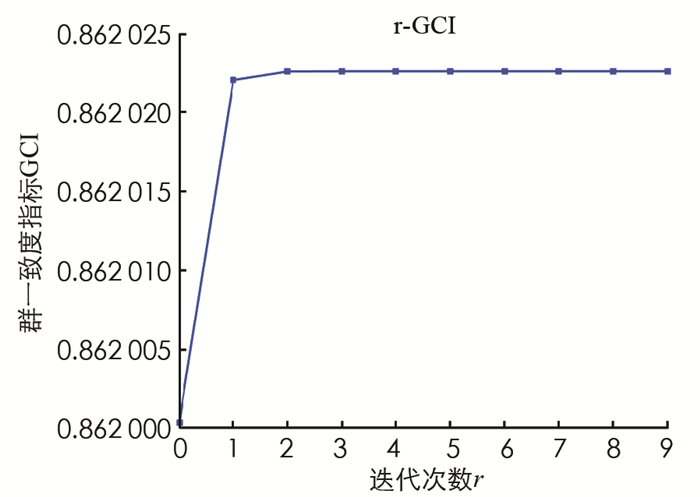
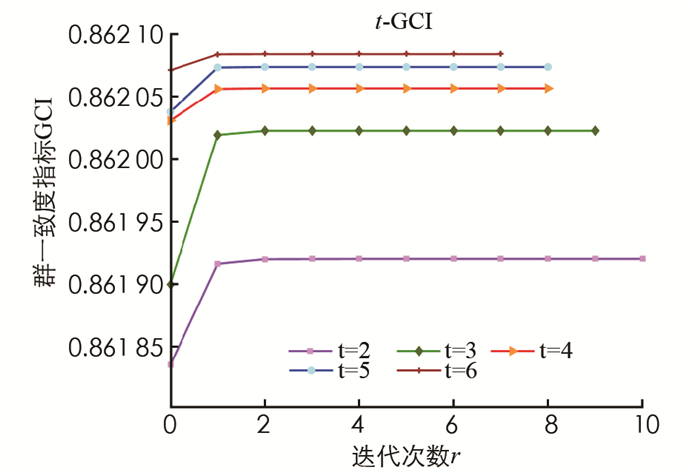
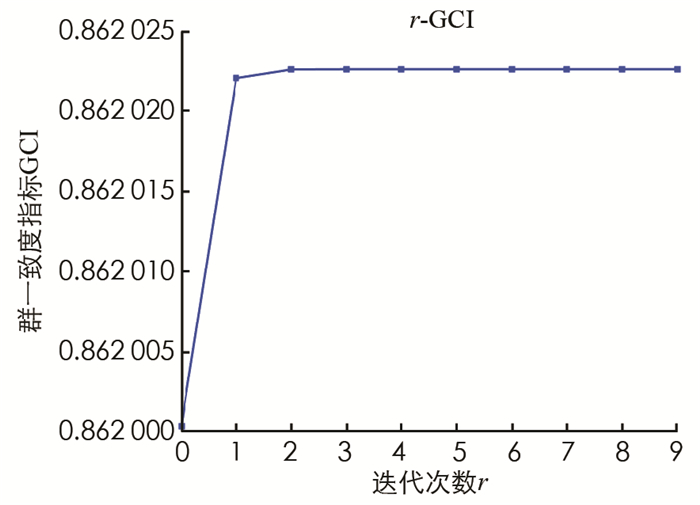
从表 6的结果可知，本研究提出的三支群决策方法能够确定对象x_i(i=1，2，3)的一致性阈值对，其中($ \tilde{\alpha}_1^{\mathrm{opt}}$，$ \tilde{\beta}_1^{\text {opt }}$)=(0.835 3，0.345 6)，($ \tilde{\alpha}_2^{\mathrm{opt}}$，$ \tilde{\beta}_2^{\text {opt }}$)=(0.836 4，0.149 3)，($ \tilde{\alpha}_3^{\mathrm{opt}}$，$ \tilde{\beta}_3^{\text {opt }}$)=(0.632 7，0.999 8). 在给定条件概率分别为Pr(C|[x₁])=0.855 5，Pr(C|[x₂])=0.125 0，Pr(C|[x₃])=0.798 0下，进一步可得，x₁属于接受决策，x₃属于边界决策，x₂属于拒绝决策. 因此能确定投资的项目为x₁和x₃，有待考虑的项目为x₂.

从上述算例的决策步骤可知，本研究提出的三支群决策方法主要由两个决策过程构成：第1个决策过程是采用算法1来获取满足一致度指标的综合代价损失函数矩阵E；第2个决策过程是建立确定语言直觉模糊三支群决策阈值的单一优化模型. 显然，采用第2个决策过程可以有效地确定一致性阈值(表 6). 下面主要讨论第1个决策过程中群一致度指标和迭代误差随迭代次数的变化趋势(图 1和图 2). 在此基础上，探究参数c和t对迭代结果的影响(图 3-图 6).

首先，由图 1和图 2可知，当迭代次数达到第2次时，群一致度指标几乎趋于稳定且收敛到较高的一致性水平，此时迭代误差趋近于零. 因此，算法1的计算效率较高且收敛速度较快.

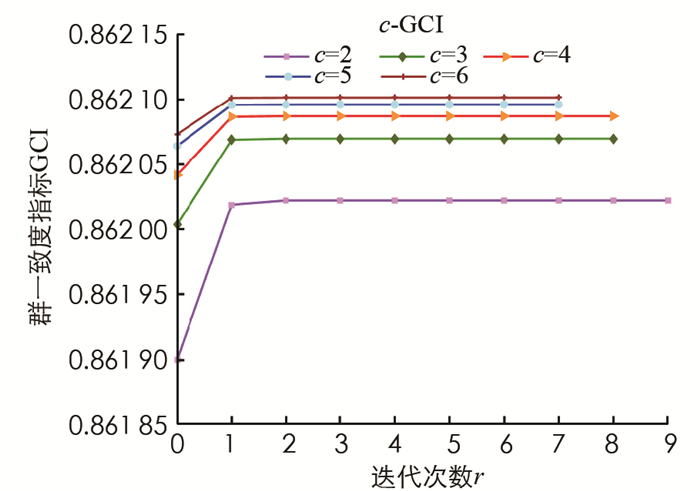
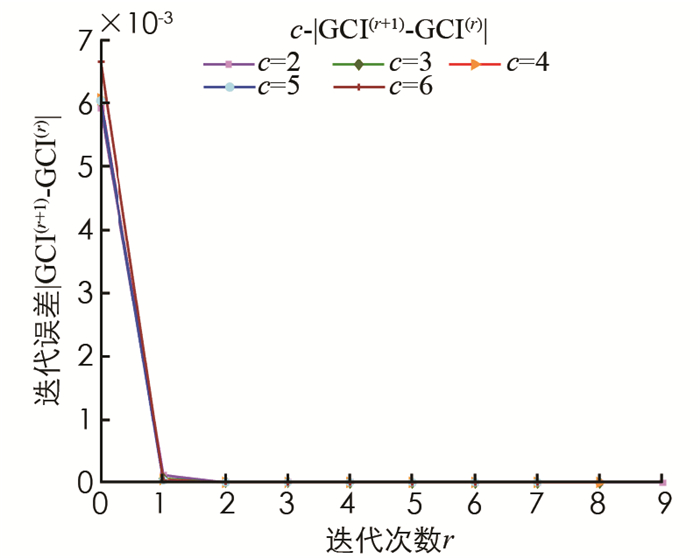
其次，从图 3和图 4可知：当参数t相同时，改变参数c，对迭代次数和群一致度指标值产生微小的影响，而对迭代误差值几乎没有影响. 另外，迭代次数随着参数c的增大呈现减小的趋势；当算法1的迭代误差达到10^-15时，群一致度指标值会随着参数c的增大呈现增大的趋势. 例如，当参数c=6，算法1在第7次迭代停止时，群一致度指标值达到最大.

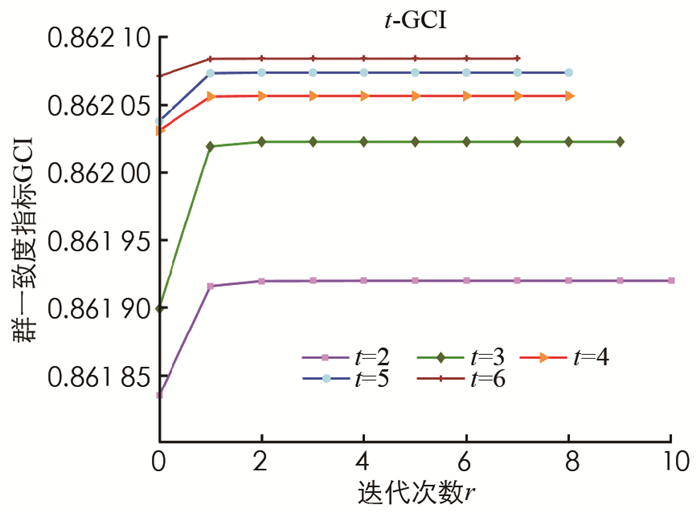
最后，图 5和图 6可得类似的结论：当参数c相同时，迭代次数随着参数t的增大呈现减小的趋势；且当算法1的迭代误差达到10^-15时，群一致度指标值会随着参数t的增大呈现增大的趋势.

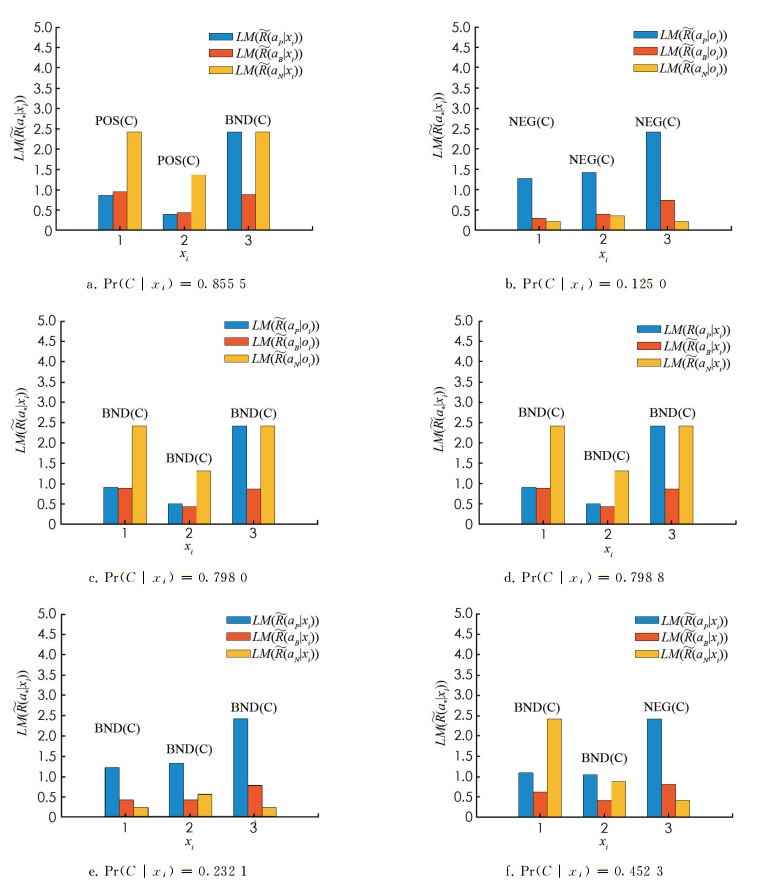
总而言之，从图 1-图 6可得，采用算法1得到的迭代结果具有一定的稳定性和准确性. 为了突出本研究提出方法的有效性和优势，本研究将所提出的方法与基于决策粗糙集的三支决策方法^[2]进行比较分析(图 7). 在算例中条件概率分别为Pr(C|[x₁])=0.855 5，Pr(C|[x₂])=0.125 0，Pr(C|[x₃])=0.798 0的前提下，采用本研究提出的方法与文献[2]的方法所获得的三支决策结果是完全一致的.

当条件概率发生变化时(即Pr(C|[x₁])=0.452 3，Pr(C|[x₂])=0.232 1，Pr(C|[x₃])=0.798 8，采用本研究提出的方法与文献[2]的方法所获得的三支决策结果亦是完全一致的，但是利用文献[2]所提出的方法需重新计算并比较排序函数值$ {LM}\left(\widetilde{R}\left(a * \mid x_i\right)\right)(*=\mathrm{P}, \mathrm{N}, \mathrm{B}, i=1, 2, 3)$才能得到三支决策结果. 而本研究提出的方法仅需将每个对象对应的条件概率与概率阈值$ \tilde{\alpha}_i^{{opt}}$和$\tilde{\beta}_i^{ {opt }} $进行比较，即可获得三支决策规则.

本研究针对基于语言直觉模糊数评价损失函数的三支群决策问题，提出了具有群体共识的语言直觉模糊三支决策方法. 该方法采用语言直觉模糊数刻画损失函数，并构造出专家个体评价矩阵，进而定义了语言直觉模糊相似测度及群体一致性指标. 其次，本研究设计了基于语言直觉模糊相似度的最优集成模型和基于权重迭代的一致性综合损失函数获取算法，并证明了该算法的收敛性. 基于该算法，获得一致性群体综合评价矩阵，并建立了语言直觉模糊三支群决策阈值的单一优化模型. 最后，采用投资策略的算例说明了所提出方法的有效性.