我们考虑配备齐次Dirichlet边界条件或齐次Neumann边界条件下的二维非线性反应扩散方程

其中：$\Delta u=\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}$，$\varOmega=[a, b] \times[a, b]$.

对方程(1)进行空间离散，令N为正整数，取空间步长$h=\frac{b-a}{N+1}$，令x_i=x₀+ih，y_i=y₀+ih，i=1，2，…，N. 利用二阶中心差分法在(x_j，y_k)处对空间进行二阶导数离散得到

从而得到半离散系统

其中：u_j，k(t)为u(x_j，y_k，t)的近似解，f_j，k(t，u_j，k(t))：=f(x_j，y_k，t，u_j，k(t)). 结合齐次Dirichlet边界条件，半离散化系统(2)可改写成矩阵形式

其中：$\boldsymbol{A}=-\frac{\alpha}{h^2}(\boldsymbol{I} \otimes \boldsymbol{K}+\boldsymbol{K} \otimes \boldsymbol{I})$，I是单位矩阵，⊗表示Kronecker积，且

若为齐次Neumann边界条件时，

在进行时间离散时，利用改进Douglas分裂方法^[12]求解半离散系统(3)，将其改写为

其中：${\mathit{\boldsymbol{A}}_1} = - \frac{\alpha }{{{h^2}}}\mathit{\boldsymbol{I}} \otimes \mathit{\boldsymbol{K}}$，$\boldsymbol{A}_2=-\frac{\alpha}{h^2} \boldsymbol{K} \otimes \boldsymbol{I}$于是得到全离散Modified Douglas Splitting格式

注意在Modified Douglas Splitting格式的每一个时间步长下，我们只需要求解一些系数矩阵为I⊗(I+$\frac{\alpha \tau}{2 h^2} \boldsymbol{K}$)或$\left(\boldsymbol{I}+\frac{\alpha \tau}{2 h^2} \boldsymbol{K}\right) \otimes \boldsymbol{I}$的线性方程组，而由Kronecker积的性质，可以转化为求解系数矩阵为三对角矩阵I+$\frac{\alpha \tau}{2 h^2} \boldsymbol{K}$的多右端项线性方程组.

由半离散系统(3)进行分析得方程(1)的精确解格式

其中：$\tilde{\boldsymbol{U}}(t)=\left[u_{1, 1}(t), \cdots, u_{N, 1}(t), u_{1, 2}(t), \cdots, u_{N, 2}(t), \cdots, u_{1, N}(t), \cdots, u_{N, N}(t)\right]^{\mathrm{T}}$，‖R_h‖≤c₁h². c₁为正常数，本文中所采用的范数‖·‖均考虑2-范数. 利用常数变易公式可得

其中，e^τA是矩阵指数. 令s=t_n+v，利用中点公式，则等式(6)可化为

因为$\boldsymbol{A}=-\frac{\alpha}{h^2}(\boldsymbol{I} \otimes \boldsymbol{K}+\boldsymbol{K} \otimes \boldsymbol{I})=\boldsymbol{A}_1+\boldsymbol{A}_2$，而A₁，A₂可交换，即A₁A₂=A₂A₁. 同时，由Kronecker积的性质，有e^A₁+A₂=e^A₁e^A₂=e^A₂e^A₁. 于是展开式(7)可得

由指数函数有理逼近得

所以可得到精确解表达为

消去式(4)中的中间变量得到数值解表达式为

假设1  假设F(t，U)满足Lipschitz条件，即存在L＞0，对∀U₁，$\boldsymbol{U}_2 \in \mathbb{R}^{N^2}$，∀t∈[t₀，T]，有

引理1  对∀τ＞0有

证  因为A₁对称负定，则A₁的特征值μ_k＜0，k=1，…，N². 于是，

同理可证A₂的情况.

定理1  若假设1成立，则Modified Douglas Splitting方法是二阶收敛的，即

其中c为正常数.

证  将精确解表达式(8)与数值解表达式(9)作差后取范数，由引理1和Lipschitz条件得

其中c₂为正常数. 由

得到

因为

所以

则有

其中：ω=‖A₁+A₂‖，c₃为正常数.将式(11)代入式(10)可得

因为A对称负定，故A=QDQ^T，其中，Q是正交矩阵，D为对角矩阵且特征值小于0.而$\left\|\mathrm{e}^{\frac{\pi}{2} \boldsymbol{A}}\right\| \leqslant \left\|\mathrm{e}^{\frac{\tau}{2} \boldsymbol{D}} \right\|=\max\limits_{\lambda \in \sigma(\boldsymbol{D})}\left|\mathrm{e}^{\frac{\tau}{2} \lambda}\right|<1$，$\left\|\tau \mathrm{e}^{\frac{\tau}{2} \boldsymbol{A}} \boldsymbol{R}_h\right\| \leqslant \tau\left\|\mathrm{e}^{\frac{\tau}{2} \boldsymbol{A}}\right\| \cdot\left\|\boldsymbol{R}_h\right\| \leqslant c_1 \tau h^2$. 于是

记$\mathrm{e}_{n+1}=\left\|\boldsymbol{U}_{n+1}-\tilde{\boldsymbol{U}}\left(t_{n+1}\right)\right\|$，令$\beta=\frac{2 L+L^2+L \omega \tau}{2}$，则

依此类推得

而由e₀=0，1+βτ≤e^βτ，则$\mathrm{e}_{n+1} \leqslant \frac{\mathrm{e}^{\alpha \tau(n+1)}-1}{\alpha}\left(c_1 h^2+c_3 \tau^2+c_1 \tau h^2+c_2 \tau^2\right)$. 记$\tilde{c}=\max \left\{c_2+c_3, c_1+c_1 \tau\right\}$，令$c=\frac{2 \mathrm{e}^{\frac{\left(T-t_0\right)\left(2 L+L^2+L \omega \tau\right)}{2}}-2}{2 L+L^2+L \omega \tau} \tilde{c}$，得到

下面给出反应扩散方程的数值算例，主要对收敛性分析进行数值验证，实验是通过Matlab实现的.

算例1  考虑二维反应扩散方程(1)，其中，Ω=[0, 1]²，t∈[0, 1]. 边界条件为齐次Dirichlet边界条件，以及初始条件

其中，扩散项为

该问题的精确解为u(x，y，t)=e^－tsin(2πx)sin(2πy). 在表 1中给出了实验结果，其中，$h=\frac{1}{N+1}$，τ=$\frac{1}{M}$，取N=19，39，79，159，319，639，M=20，40，80，160，320，640时，计算给定空间步长与时间步长下，数值解与精确解的最大模误差、对应的收敛阶和计算时间，相应的计算结果如表 1所示.

通过表 1的结果，我们可以得出误差关于h，τ是二阶精度的，与收敛性分析是一致的.

算例2  考虑三维反应扩散方程

其中：Ω=[0, 1]³，t∈[0, 1]. 边界条件为齐次Dirichlet边界条件，以及初始条件

其中，扩散项为

该问题的精确解为u(x，y，z，t)=e^－tsin(2πx)sin(2πy)sin(2πz). 在表 2中我们给出了实验结果，其中，$h=\frac{1}{N+1}, \tau=\frac{1}{M}$，取N=19，39，79，159，M=20，40，80，160时，计算给定空间步长与时间步长下，数值解与精确解的最大模误差、对应的收敛阶和计算时间，相应的计算结果如表 2所示.

通过上表的结果，我们可以得到三维反应扩散方程可以利用同样的方法进行求解，得到的误差关于h，τ也是二阶精度的.

算例3  考虑二维Schnackenberg方程组

其中：Ω=[0，L]²，t∈[0，T]. 边界条件为齐次Neumann边界条件，以及初始条件

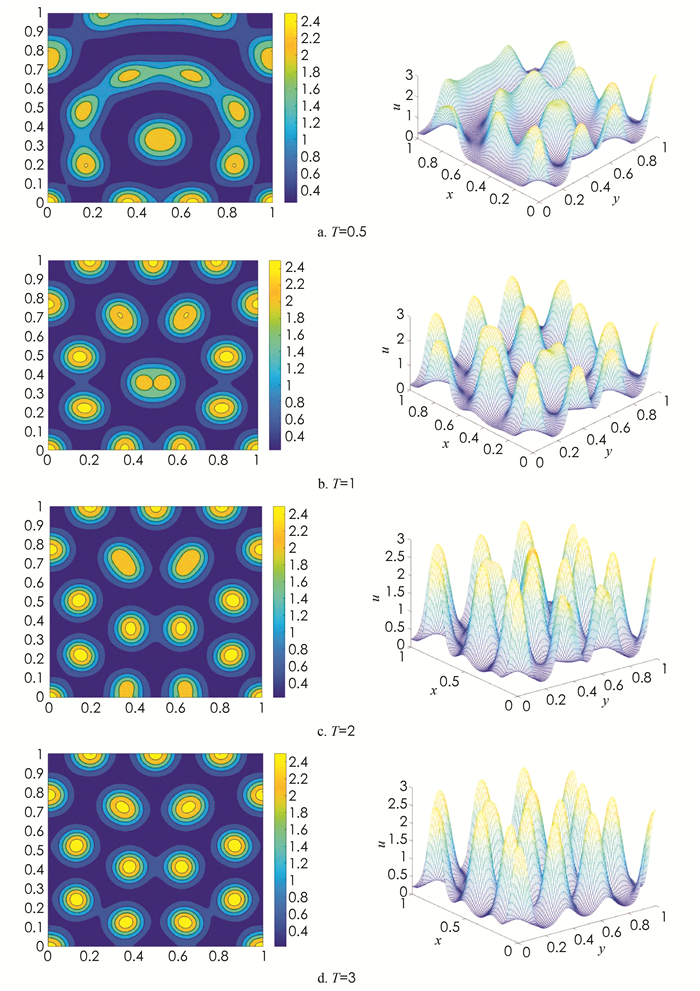
该方程组没有精确解，利用该方法进行求解.取N=101，M=8 000时，其中，a=0.130 5，b=0.769 5，γ=100，K_u=0.05，K_v=1，当L=1，T=0.5，1，2，3时，得到数值解u(x，y，t)的图像如图 1所示.

参考文献^[12]中针对反应扩散方程提出了一类二阶改进Douglas分裂方法，该方法具备良好的稳定性且计算速度快的特点，但作者仅仅给出了该方法针对线性问题的半离散误差分析. 而本文主要采用空间二阶中心差分方法对空间方向进行离散，利用改进Douglas方法对时间方向进行离散得到相应的Modified Douglas Splitting全离散格式. 对该格式进行收敛性分析，证明该全离散格式关于空间和时间步长是二阶收敛的结论. 最后借助相关数值实验算例进行收敛性验证.