重庆市中心城区由北碚、巴南、沙坪坝、渝北、南岸、渝中、江北、九龙坡和大渡口等9个区组成，其中设有气象机构的为北碚、巴南、沙坪坝、渝北4个区. 本文选取重庆市中心城区北碚、巴南、沙坪坝、渝北4个区及周边区域璧山、合川、铜梁3个区为主要研究区域.

本文采用的2017-2019年逐日O_{3_8H}环境监测数据为重庆市环境监测中心提供，同期气象资料为重庆市气象信息与技术保障中心提供的国家气象站地面气象观测资料，包括平均气温(T)、最高气温(T_max)、相对湿度(RH)、降水量(R)等常规气象观测数据.

KNN(K-NearestNeighbor)数据挖掘算法是经典的分类与回归分析的邻近算法，即K最近邻，就是每个样本都可以用它最接近的K个邻近值来代表. 邻近算法是将数据集合中每一个记录进行分类的方法^[19]，在气象的研究中，其主要原理是通过在历史数据库中查找与未来相似背景下的相似样本，并依据排序结果客观赋予权重，根据不同权重下的历史样本预报结果. KNN算法在预报空气污染和霾等级分类中效果较好，准确率达到了80%~90%^[20-21]. 本文的基本算法是假设预报日的平均气温、最高气温、相对湿度、降水量等气象要素为预测样本，臭氧浓度实测值为标志量，在训练样本集合中找到与预测样本最相似的K个近邻，然后找出K个标志量，最后按照投票多数原则，选取最多的标志量为预测样本预测结果. 因此，KNN算法也是一种相似算法.

BP神经网络算法是目前应用最广的预测方法，不少学者将神经网络模型应用于环境气象等方面的研究，取得了较好的成果^[22-24]. 其基本思想是：该算法工作信号正向传递和误差信号反向传递两个子过程，学习规则和目标使用最速下降法，通过反向传播不断调整网络的权值和阈值，使全局误差系数最小，学习本质是对连接权值的动态调整. 基本结构由输入层、隐层和输出层构成^[25].

对预测模型精度的评价主要采用相对误差值、绝对误差值和臭氧浓度预测准确率^[26]进行比较. 其中相对误差值与绝对误差值越小，说明预测精度越高；若臭氧浓度预测准确率小于0，均按0处理.

反距离加权插值法^[27]是基于地理学第一定律相近相似的原理，认为每个采样点对邻近区域的插值点有一定的影响，且影响的大小随距离的增大而减小. 该插值法的特点是可以保证插值结果在采样点位与实际值一致.

通常使用的机器学习算法将数据样本分为训练集与测试集，通过训练集数据来建立模型，测试数据则用于检验模型的泛化能力^[28]. 因此在确定建立模型前，为消除指标之间的量纲影响，需对数据进行归一化处理. 本文采用对数据分段建模方式进行拟合，确定2017-2018年731个有效臭氧浓度数据作为训练集数据，2019年逐日数据作为检验数据，再结合平均气温、最高气温、相对湿度、降水量等4个气象因子，以臭氧浓度为输入目标，基于KNN数据挖掘算法和BP神经网络算法，分别构建7个区的预测模型.

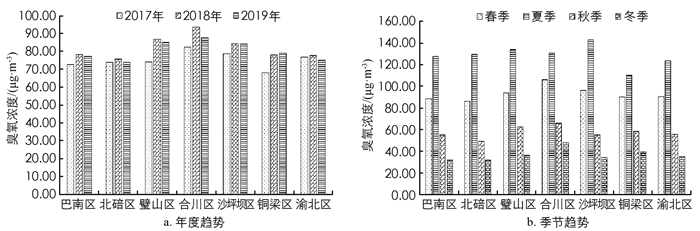
绘制2017-2019年研究区臭氧浓度趋势图(图 1). 图 1a可知，除铜梁区和沙坪坝区呈逐年上升趋势，北碚区及其他区最大值均出现在2018年，3年趋势呈“单峰形”；从图 1b可知，研究区臭氧浓度季节变化均为夏季浓度最高，冬季最低，其中沙坪坝区夏季浓度最高，铜梁区夏季浓度最低，北碚区夏季臭氧浓度在整个研究区中为第三高，但冬季浓度最低.

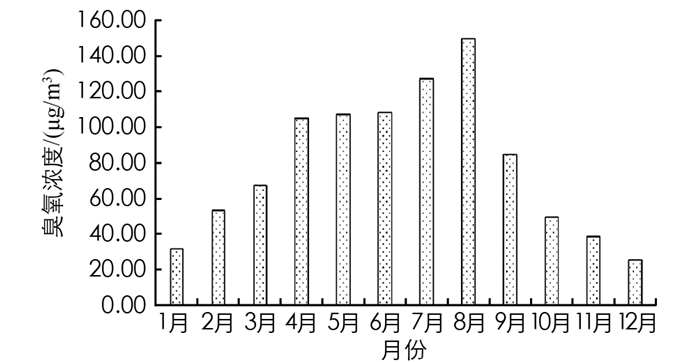
图 2为研究区月平均臭氧浓度趋势图. 由图 2可知，2017-2019年7个区臭氧浓度的月平均浓度呈单峰型，其中8月最高，12月最低，即从1月起，每月的臭氧浓度都呈增加趋势，8月达到峰值后开始逐月降低.

2017-2019年研究区臭氧日浓度与4种气象要素的相关性如表 1所示. 从表 1可看出，7个区臭氧浓度与气象要素密切相关，对比分析发现，除降水量与臭氧浓度呈弱相关性外，其余3个气象要素均与臭氧浓度呈较强相关性，其值均大于0.6，其中关系最密切的是最高气温，其次是平均气温，说明臭氧浓度的变化受温度的影响较大. 臭氧浓度与相对湿度呈负相关性，这是因为空气水汽中含有较多的H，OH等自由基，可以分解臭氧中的氧分子，从而使臭氧浓度降低^[24]. 臭氧浓度与降水量相关性较低，最大相关系数也接近0.1，说明研究区降水与光化学反应效率关系不明显. 总体来说，臭氧浓度与气象要素关联度由强到弱依次为最高气温、平均气温、相对湿度、降水量.

本文利用SPSS Modeler软件、采用KNN数据挖掘算法对2017-2018年研究区的臭氧浓度进行建模预测，预测值与实测值对比结果见表 2. 由表 2可知，KNN模型在训练模型中准确率均在75%以上，7个区模型的平均准确率为77.3%，其中合川区模型的准确率最高，达79.7%，巴南区模型的准确率最低，只有75.3%，北碚区模型的准确率为78.3%，高于平均准确率；从决定系数来看，北碚区决定系数为0.892，高于其余6个区，铜梁区决定系数最低只有0.701，其余区决定系数在0.82~0.87之间，模拟效果较好. 7个区模型平均相对误差为0.29，其中合川区误差最小(0.23)，璧山区误差最大(0.34)；7个模型平均均方根误差为22.5，其中铜梁区误差最大(24.47)，北碚区误差最小(18.93). 综上可见，基于地面气象要素建立的KNN模型可以较好地模拟预测污染物的浓度.

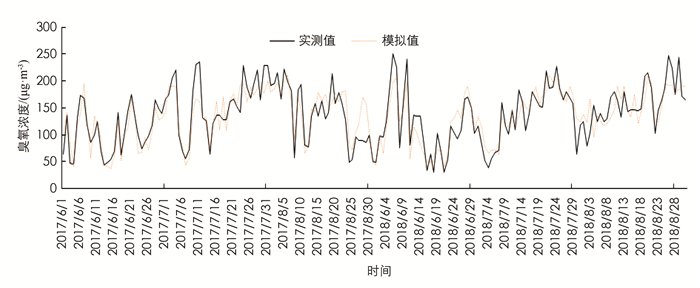
图 3为2017-2018年北碚区夏季臭氧浓度值与实测值趋势对比图，从图中可看出，臭氧浓度模拟值与实测值趋势基本一致，但是有部分模拟值低于实测值.

对2019年研究区的臭氧浓度进行预测检验，将预测值与实测值对比得到表 3，由此可知，KNN模型在检验模型中准确率略低于训练模型，7个区KNN模型的平均准确率为74%，比训练模型准确率低3.3%，其中北碚区的KNN模型准确率最高，为78.60%，较训练模型高0.3%；铜梁区的KNN模型准确率最低，只有70.40%，较训练模型低了7.5%；从决定系数来看，北碚区决定系数在0.9左右，铜梁区决定系数最低，其余区的决定系数在0.7~0.8之间，模拟效果较好. 7个区的模型平均相对误差为0.33，其中北碚区误差最小，为0.23，渝北误差最大，为0.40；7个区KNN模型均方根误差与训练模型结果基本一致，铜梁区误差最大，北碚区误差最小.

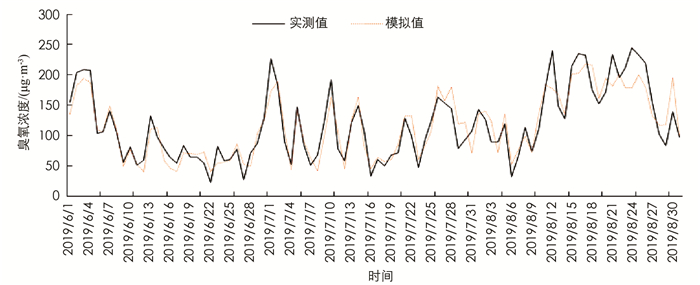
图 4为2019年北碚区夏季臭氧浓度的模拟值与实测值趋势图，从图中可看出，该区臭氧浓度模拟值与实测趋势基本一致，两者之间的误差波动不大，平均相对误差0.18，其中最大误差0.9.

利用BP神经网络算法对2017-2018年研究区的臭氧浓度进行预测，将预测值与实测值对比得到表 4. 由表 4可知，BP神经网络算法在训练模型中准确率均在74.57%以上，7个区的平均准确率为74.6%，其中合川区的准确率最高，为77.50%，璧山区的模型准确率最低，只有71.60%，北碚区的准确率为74.30%，略低于平均准确率；从决定系数来看，北碚区决定系数高于其余6个区的模型，铜梁区最低，只有0.711，其余区的决定系数在0.758~0.840之间，模拟效果较好. 7个区的模型平均相对误差为0.34，其中合川区误差最小为0.26，巴南区误差最大为0.39；7个区的模型平均均方根误差为22.50，其中璧山区误差最大(29.52)，北碚区误差最小(21.59). 综上可见，基于地面气象要素建立的BP神经网络算法可以较好地模拟预测臭氧浓度.

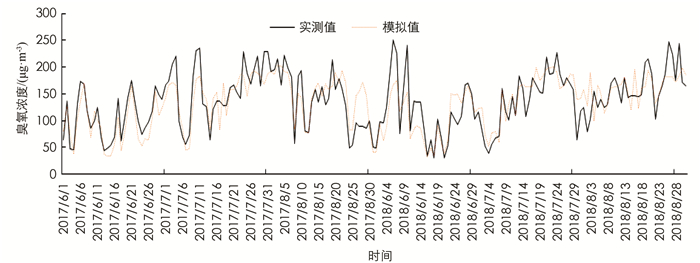
图 5为2017-2018年北碚区夏季臭氧浓度的BP模拟值与实测值趋势图，从图中可看出，夏季臭氧浓度模拟值与实测值趋势基本一致，平均相对误差0.18，其中最大误差1.02.

对研究区2019年的臭氧浓度进行预测检验，将预测值与实测值对比得到表 5. 由表 5可知，BP神经网络算法构建的模型在检验模型中准确率略高于训练模型，7个区的模型平均准确率为75.68%，比训练模型准确率高1.1%，其中合川区的模型准确率最高为78.50%，较训练模型高1%的准确率；巴南区的模型准确率最低只有73.90%，较训练模型高了1.1%，北碚区的检验模型准确率也较训练模型高了2.2%；从决定系数来看，北碚区系数在0.86以上，高于其余6个区，璧山区决定系数最低，其余区的决定系数在0.815~0.851之间. 7个区的模型平均相对误差为0.29，其中合川区误差最小(0.25)，巴南区误差最大(0.38)；7个区的模型均方根误差与KNN模型结果一致，铜梁区误差最大，北碚区误差最小.

图 6为2019年北碚区夏季臭氧浓度的BP模拟值与实测值趋势图，从图中可看出臭氧浓度模拟值与实测值趋势基本一致，两者之间的误差波动在8月，平均相对误差0.18，其中最大误差0.9.

本文分别基于KNN数据挖掘算法与BP神经网络算法，构建了2017-2019年臭氧浓度预测模型，并对2种预测模型的预报效果进行对比检验，筛选最优预测模型. 结果表明，2种预测模型在7个区的训练中平均预报准确度超过了74%，其中KNN模型的准确率高于BP神经网络模型，2种模型与实测值的相关性超过了0.7，拟合度较高. 在验证模型准确率中，KNN预测模型趋势与BP神经网络模型比较，BP神经网络模型在检验过程中的效果高于训练效果，平均误差也低于训练值；同时从北碚区预测结果来看，基于BP神经网络模型的预测结果总体优于KNN模型. 总体来说，基于BP神经网络模型更优于基于KNN数据挖掘算法的预测模型.

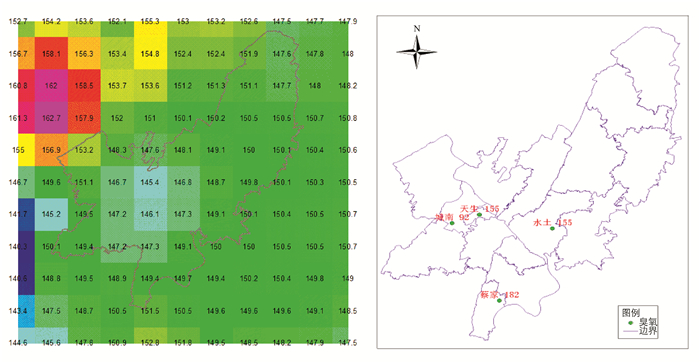
根据上文分析，以BP神经网络模型为预测模型，选取研究区2020年6月1日平均气温、最高气温、相对湿度、降水量等4个气象因子为预测要素，预测6月1日研究区臭氧浓度，并采用ArcGIS空间分析模块中的反距离加权插值法计算、绘制未来24 h分辨率为5 km的研究区臭氧浓度网格预报图(图 7)，将预测值与实测值进行对比检验. 根据图 7a可知，北碚区未来24小时臭氧浓度在145~153 μg/m³之间，低值区出现在北碚城区，高值区为研究区北部，即与合川区交界的一带. 与北碚区6月1日实测值(图 7b)对比，其余区的实测值在92~155 μg/m³范围，预测值高值与实测值基本一致，低值差距较大. 从地理位置来看，实测值的低值与预测的低值位置基本一致，位于研究区中部偏西，而实测高值预测区域差距较大，位于研究区南部和东部. 造成预测误差的原因主要是因为臭氧是二次生成的光化学污染物，生成和积累的时间主要集中在白天，同时北碚区水土和蔡家这两个监测点位于发展区，存有大量的在建工地，易产生大量的VOCs(挥发性有机物)不利于污染物扩散.

为探索不同机器学习方法在臭氧浓度预测中的应用效果，本文利用KNN数据挖掘算法与BP神经网络算法，挑选与臭氧密切相关的平均气温、最高气温、相对湿度、降水量等4个气象因子，建立2017-2019年以重庆中心城区北碚区为中心的臭氧浓度预报模型，并运用反距离加权插值法将臭氧浓度预报值网格化，得到以下结论：

1) 2017-2019年间，除铜梁区和沙坪坝区呈逐年的上升趋势外，北碚区及其他区的趋势呈“单峰形”，最大值出现在2018年. 北碚区及其周边区域的臭氧浓度季节变化是一致的，夏季浓度最高，冬季浓度最低，且逐月平均臭氧浓度呈单峰型，8月最高，12月最低. 臭氧浓度与气象要素密切相关，除了降水量与臭氧浓度呈弱的负相关性外，其余3个气象要素均与臭氧浓度相关性较强，均大于0.6.

2) 基于KNN数据挖掘算法与BP神经网络算法，构建了2017-2019年臭氧浓度预测模型，并对2种预测模型的预报效果进行对比检验，筛选最优预测模型. 结果表明，2种预测模型在7个区的训练中平均预报准确度超过了74%，其中KNN模型的准确率高于BP神经网络模型，2种模型与实测值的相关性超过了0.7，拟合度较高. 在验证模型准确率中，KNN模型预测趋势与BP神经网络模型比较，BP神经网络模型在检验过程中的效果高于训练效果，平均误差也低于训练时；同时从北碚区预测结果来看，基于BP神经网络模型的预测结果总体优于KNN模型.

3) 采用ArcGIS空间分析模块中的反距离加权插值法计算北碚区臭氧浓度网格预报，发现北碚区域内未来24小时臭氧浓度预测在145~153 μg/m³之间，高值与实测值基本一致，低值低于实测值. 从地理位置来看，低值与实测值位置基本一致，在中部偏西，高值预测区域差距较大，实测高值区在南部和东部.

综上所述，在运用2种机器学习方法对臭氧浓度进行模拟预测中，BP神经网络算法在臭氧浓度的预测中有更好的表现；其次臭氧作为二次污染物，受气象和前体物等因素的影响的同时，也受污染物区域传输以及传输过程中前体物的光化学反应的重要影响^[29]，而预测模型主要基于气象条件的影响，因此预测值较实测值有所偏差.