-
现实生活中,数据往往存在不确定性. 有些模型能很好拟合已持有的数据,但进行预测时却与真实情况相差较大,误导决策者做出错误的决策[1]. 模型平均的出现解决了这一问题,使预测模型变得更加稳定.
传统的变量选择方法代表是:赤池信息量准则(Akaike's information criterion,AIC)由文献[2]在研究信息论尤其是在解决时间序列的定阶问题时提出,现常被用于处理模型选择,评估模型的复杂度等属性.
目前经典的模型平均法有两类:频率模型平均法FMA[3-4]和贝叶斯模型平均法BMA[5-6](核心思路是通过后验概率来分配权重).
文献[7]提出的超高维回归下的模型平均法中,考虑了预测因子数量p超过样本容量n的高维回归问题,为高维回归问题开发了一个新的模型平均程序,主要研究了该方法下的渐近最优性和模型的权重赋予. 文献[8]提出的水手刀模型平均法是一类分位数回归模型平均(quantile regression model averaging). 为了考虑分位数回归模型中的误差项和解释变量之间的相关性,提出了一种重叠模型平均估计模型,该方法证明了在最小化样本外最终预测误差方面的渐近最优性.
这些研究表明,模型平均预测参数通常会比单一的模型选择方法预测的参数实现更低的估计、预测误差和风险. 传统的SAIC方法尽管表现较好,但耗时极长. 本文提供一种新的模型平均思路用以提升模型的稳定性、准确性和运行速度.
全文HTML
-
假设有k个模型,根据文献[2]有其中第i个模型中赤池信息量为
其中:Li为第i个模型的似然函数,pi为第i个模型的参数.
由于本文是纵向数据,并且采用的是广义估计方程用于预测,使用拟似然函数计算赤池信息量过于冗杂,本文通过残差平方项代替似然函数项. 将第i个模型的赤池信息量变为:
其中:残差平方和
$ R S S_i=\left\|Y-\hat{Y}_i\right\|^2 ; N=\sum\limits_{i=1}^m n_i$ 为纵向数据中的样本数. 在样本数相同的不同广义估计方程中,N的值都是相等的.在所有的k个模型中,每个模型对应一个赤池信息量. 从k个赤池信息量中选出赤池信息量最小的模型,将该模型作为预测模型,记为mAIC(minimum AIC model).
-
文献[3]较为详细提到了SAIC模型平均法. 其中详细说明了模型平均法的思路和SAIC方法的推导,并主要研究了模型的权重赋值.
由赤池信息量的定义
我们不难通过变形得到两个拥有不同参数量和似然函数模型的赤池信息量函数比值
值得一提的是,在惩罚项相等的时候,该函数会变为似然函数的优势比.
由(2)式可以得到一个关于模型权重ωk的计算公式. 假设有K个子模型做模型平均,则第k个子模型在该模型平均中分配到的权重为
由该方法得出的模型权重有以下特点:
1) 拥有相同赤池信息量的模型具有相同的权重.
2) 假设利用K个子模型做模型平均,这些权重将仅与赤池信息量有关,和惩罚项无关(他们拥有相同的变量数p).
3) 拥有更小赤池信息量的模型具有更大的权重.
-
本文研究的纵向数据数据结构的参数和符号说明如下:
设
$\left\{\left(y_{i j}, x_{i j}\right) ; j=1, 2, \cdots, n_i\right\}$ 是第$i$ 个个体的观测,其中$(i=1, 2, \cdots, m)$ ,设置$\boldsymbol{y}_i\left(n_i \times 1\right)=\left(y_{i 1}\right.$ ,$\left.y_{i 2}, \cdots, y_{i n_i}\right)^{\mathrm{T}}$ ,且$\boldsymbol{X}_i\left(n_i \times p\right)=\left(x_{i 1}, x_{i 2}, \cdots, x_{i n_i}\right)$ ,则纵向数据为如下线性回归模型其中:
$\boldsymbol{y}$ 为$(N \times 1)$ 的向量,$\boldsymbol{y}=\left(y_1^{\mathrm{T}}, y_2^{\mathrm{T}}, \cdots, y_m^{\mathrm{T}}\right)^{\mathrm{T}}, \boldsymbol{X}$ 为$(N \times p)$ 维的矩阵,$\boldsymbol{X}=\left(\boldsymbol{X}_1^{\mathrm{T}}, \boldsymbol{X}_2^{\mathrm{T}}, \cdots \boldsymbol{X}_m^{\mathrm{T}}\right)^{\mathrm{T}}$ , 残差项$\boldsymbol{\varepsilon}$ 的维度同$\boldsymbol{y}$ 一致, 且服从多元正态分布$\boldsymbol{\varepsilon} \sim N(0, \boldsymbol{\varSigma}), \boldsymbol{\varSigma}$ 为$N \times N$ 阶的分块对角矩阵, 即通常情况下,自变量p越多,样本量N需要得就越多,因此我们要求N>p.
-
MSAIC的核心思路是:在拥有相同参数数量的所有子集中选取p个(p为数据的协变量数)赤池信息量最小的模型,并对这p个模型进行加权. 具体步骤如下:
参数数目为1的子集为
$\left(\boldsymbol{X}_1, \boldsymbol{X}_2, \cdots, \boldsymbol{X}_P\right)$ , 从中选取赤池信息量最小的模型$\left(\boldsymbol{X}_{k 1}\right)$ ; 参数数目为2的子集有$\left(\boldsymbol{X}_1, \boldsymbol{X}_2\right), \left(\boldsymbol{X}_1, \boldsymbol{X}_3\right), \cdots, \left(\boldsymbol{X}_{p-1}, \boldsymbol{X}_p\right)$ , 从中选取赤池信息量最小的模型$\left(\boldsymbol{X}_{l 1}, \boldsymbol{X}_{l 2}\right)$ . 重复此动作共$p$ 次, 挑选出$p$ 个子集基于广义估计方程,p个子模型共能算出p个估计方程:
$\left(f_1(\cdot), f_2(\cdot), \cdots, f_p(\cdot)\right)$ .代入数据后可以得出p个关于Y的拟合值组成的向量:
利用SAIC加权法,对这p个子集基于SAIC方法进行加权. 这p个子集可以得到p个赤池信息量. 第i个模型的赤池信息量变为
该模型的权重
$\omega_i$ 的计算方式由此可获得p个模型的权重(ω1,ω2,…,ωp).
相较传统的SAIC方法,该计算量从约p!降低为(2p-1).
在模型(7)中代入数据后能得出Y的估计值
$\overset{\wedge }{\mathop{\boldsymbol{Y}}} $ :该模型平均方法仅对传统的SAIC模型平均法的最后的加权步骤进行了改进,计算量仍然巨大,为解决这一问题,本文进一步提出了MOSAIC以降低模型平均法的计算量.
-
MOSAIC(Minimum Onward Smooth AIC),是MSAIC的改进方法,借鉴了逐步回归向前法(Forward Stepwise). MOSAIC的具体步骤如下:
1) 从参数数量为1的子模型中选择拥有最小赤池信息量(共需计算p个模型)的子模型(Xk1).
2) 在参数数量为2的所有子模型中(共需计算(p-1)个模型),从拥有(Xk1)的子模型中,选择拥有最小AIC的子模型(Xk1,Xk2). 重复此行为,直至将所有参数加入到子模型(Xk1,Xk2,…,Xkp)中,挑选出p个子集,基于广义估计方程算出p个估计方程:
3) 利用SAIC加权法,仅对这p个子集基于SAIC方法进行加权,得到p个权重(ω1,ω2,…,ωp). 代入数据后能得出Y的估计值
该计算量相较本章第一小节提出的MSAIC方法的计算量,从(2p-1)降低为
$\frac{p(p+1)}{2} $ .该模型平均方法虽然对MSAIC进行了改进,但其计算量仍然较大,在维度较高的数据中仍难以快速输出结果. 为解决这一问题,本文进一步提出了MOOSAIC.
-
MOOSAIC (Margin Overweighted of Smooth AIC),是MOSAIC的改进方法.
1) 计算参数数量为1的所有子模型的赤池信息量(共需计算p个模型),并依据该赤池信息量按从小到大的顺序,对子模型进行排序
p个子模型所示
其中第i个模型为
基于广义估计方程,p个子模型能算出p个估计方程
基于SAIC方法,对p个模型的赤池信息量进行加权,得到p个权重(ω1,ω2,…,ωp),代入数据后能得出Y的估计值:
与MOSAIC相比,
$\overset{\wedge }{\mathop{\boldsymbol{Y}}}$ 的计算量从$\frac{p(p+1)}{2}$ 降低为$(2 p-1)$ . -
将MOSAIC模型输出的残差平方和与MOOSAIC模型输出的残差平方和进行加权,且权重变化非线性,可以给出其权重公式:
MOSAIC和MOOSAIC的加权模型为
记为MO&MOO模型.
该模型为MOSAIC和MOOSAIC利用指数进行的简单加权. 引入该模型是为说明:并非加权模型的部头越大,模型拟合效果就越好越稳定. 之后的结果,无论是预测精度还是稳定效果,MO&MOO模型都远不如它的两个组成部分:MOOSAIC模型和MOSAIC模型.
3.1. MSAIC
3.2. MOSAIC
3.3. MOOSAIC
3.4. MO&MOO加权模型
-
本章借助高维纵向数据的模型平均估计[9]生成模拟数据,并在此基础上对模拟数据的各项参数进行调试,以确保模型预测的稳定性和精准性. 本章模拟研究的抽样方法采用的是Bootstrap自助法,随机挑选训练集和测试集,并用不同方法进行拟合,重复该过程100次,之后将对这100次拟合得到的预测残差平方和进行研究. 评价模型预测效果的标准是:预测残差平方和的中位数和四分位差.
-
生成模拟数据用于实验. 过程如下:
其中:
$\mu_{i j}=\sum_{k=1}^p x_{i j, k} \beta_k+\varepsilon_{i j}, i=1, 2, \cdots, m, j=1, 2, \cdots, n_i, m$ 为总个体数,$n_i$ 为每个个体内的观测数,总样本数为$\sum_{i=1}^m n_i ; \beta_k, k=1, 2, \cdots, p$ ,共生成p个模拟变量的系数,其中有s个真实变量由均值为0,标准差为0.5的正态分布生成; 其余虚假变量值设置为0,生成的数据是p维数据. 解释变量的均值为0p. 其中,多元数据的协方差矩阵为由于本文计算赤池信息量时使用的方法是利用残差平方和代替似然函数,因此默认残差服从正态分布. 为了研究残差服从正态分布是否会对模型预测产生较大影响,本文在之后的实验中对残差项不断进行重复实验,以确保在极端残差情况下仍能保持预测的稳定性.
将随机误差项设为c×AR(1),其中:AR(1)过程为
c为调整随机误差项的一个压缩参数,
$v_{i, j}$ 服从正态分布N(0,1). 初始c值为1,初始ρ值为0.5.考虑如下的具体设计:令
从总体500个个体中挑选350个个体作为训练集,150个个体作为测试集,即训练集样本量为2800,测试集为1200.
在实验中,我们将提出的模型平均估计量MOOSAIC记为moo,MOSAIC与MOOSAIC加权拟合模型平均记为mo&moo,逐步回归法最小AIC模型选择记为mAIC,Scad模型选择记为ex_scad,Lasso模型选择记为ex_lasso和全模型,并进行横向比较.通过计算不同模型下的残差平方和来比较各种方法的优劣,重复100次实验,每次实验输出7个模型的残差平方和,利用残差平方和绘制箱型图来对比各模型的优劣,同时给出了不同情况下预测残差平方和的上四分位数、中位数和下四分位数与四分位差的统计表(表 1-5),其中:1st Qu.表示下四分位数; Median表示中位数; 3rd Qu.表示上四分位数; Qu.Deviation表示四分位差; 箱型图中纵坐标为残差平方和.
-
实验1 变动协方差矩阵
保持自回归模型里的常系数0.2和压缩参数1不变,通过控制自回归模型里的常系数和压缩参数,使得协方差矩阵中的d值分别取0.1,0.5,0.9,各方法预测残差平方和箱型图见图 1,预测残差平方和的上四分位数、中位数和下四分位数与四分位差见表 1-3.
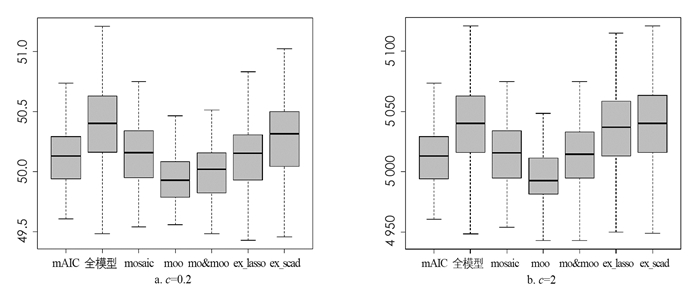
实验2 变动压缩参数
通过控制协方差矩阵中的d值为0.5且保持自回归模型里的常系数0.2不变,使得压缩参数c依次取0.2和2,各方法预测残差平方和箱型图见图 2,预测残差平方和的上四分位数、中位数和下四分位数与四分位差见表 4-5.
4.1. 模拟生成数据
4.2. 模拟实验
-
为解决SAIC模型在大数据下面临运算时间长的困境,本文提出了MSAIC,MOSAIC,MOOSAIC 3种基于SAIC方法的模型平均法. 提升SAIC方法下的运行效率、预测精度和预测稳定性所需运行时长从大到小排序依次为MSAIC,MOSAIC和MOOSAIC. 通过数值实验将3种方法与多种经典预测方法,如Lasso,Scad等方法进行比较最后结果验证了MOOSAIC最大幅度提升了运行效率、运行精度和预测稳定性,且运行时长从数量级p!降低为数量级(2p-1).




 下载:
下载: