-
设{Xn,n≥1}为独立同分布的随机变量序列,其公共分布函数为F(x). 若存在常数an>0,bn∈
$ \mathbb{R}$ 使得对所有1+γx>0,有其中
$G_\gamma(x)=\exp \left\{-\left(1+\gamma_x\right)^{-\frac{1}{\gamma}}\right\}, \gamma \in \mathbb{R} $ ,则称F属于极值分布Gγ的吸引场,记为F∈D(Gγ),γ为极值指数. 当γ>0时,(1)式等价于其中
$U(t)=\frac{1}{(1-F)^{\leftarrow}(t)} $ .当分布函数F未知时,对极值指数γ的估计是极值理论的一个重要组成部分,受到了学者的广泛关注,常用于金融、保险、自然灾害等领域. 在分布函数形式未知的情况下,文献[1]提出了著名的Hill估计量,推断分布函数的尾部表现;文献[2-4]在一定条件下证明了Hill估计量的相合性和渐近正态性;文献[5]提出了矩率估计量,并给出了其分布表示;文献[6]提出了一系列基于二阶参数的外部估计得到的渐近无偏估计量,并证明了其渐近性质;文献[7]证明了包含Hill估计量和矩率估计量在内的一系列尾指数估计量的渐近正态性. 关于尾指数估计量的更多研究,见文献[8-10].
在大数据时代,估计极值指数时,常常会遇到被分开存储的数据,例如分析来自不同保险公司的保险索赔时,为了保护客户的隐私,保险公司不能向外部分享具体的数据,甚至不能分享任何索赔结果,此时前文所提的Hill估计量和矩率估计量等都不可用. 与大部分尾指数估计量的相关文献一样,Hill估计量等只使用了一部分秩序较高的统计量. 文献[11]和文献[12]基于块方法提出了DPR估计量. 当数据被分组储存且每组只有少数几个最大的样本可用于分析时,DPR方法是可行的,但是它仅使用了每块中最大的两个样本,很可能并不是尾指数的充分统计量.
而分治算法可以分析存储在多台计算机中的数据集,分别估计每台机器上的参数,并将结果发送到中央机器. 中央机器通过简单的平均来结合所有结果,以获得计算可行的估计量. 设独立同分布的样本X1,X2,…,Xn存储在k个机器中,每个机器存储m个观测,令Mj(1)≥Mj(2)≥…≥Mj(m)表示存储在机器j内的样本次序统计量,文献[13]基于Hill估计量提出如下分布式Hill估计量
其中,d为一个确定的整数,表示每个机器所使用的超过门限值的个数.
$\hat{\gamma}_{\mathrm{DH}} $ 是极值指数的一个相合估计量,且在二阶正规变换条件下具有渐近正态性.受文献[13]启发,本文基于矩率估计量提出如下分布式矩率估计量
并研究其相合性和渐近正态性,中间序列k=k(n)满足当n →∞时,
为了证明其渐近正态性,我们需要文献[14]中的二阶条件,即存在一个最终或正或负的函数A,且
$ \lim\limits _{t \rightarrow \infty} A(t)=0$ ,和一个实数ρ≤0,使得
全文HTML
-
定理1 假设(2)式及(5)式成立. 当n→∞时,
$\hat{\gamma}_{\mathrm{DMR}} \stackrel{P}{\longrightarrow} \gamma $ .定理2 假设(5)式及(6)式成立. 当n→∞时,若
$ (k d)^{\frac{1}{2}} A\left(\frac{m}{d}\right)=O(1)$ 成立,则其中
-
设独立同分布的样本X1,X2,…,Xn存储在k个机器中,每个机器存储m个观测,令Mj(1)≥Mj(2)≥…≥ Mj(m)表示存储在机器j内的样本次序统计量. Zj(1)≥…≥Zj(m)表示对应于Mj(1)≥…≥Mj(m)的服从Pareto(1)分布的次序统计量,则由文献[14]知
$ \left\{M_j^{(i)}\right\}_{i=1}^m \stackrel{d}{=}\left\{U\left(Z_j^{(i)}\right)\right\}_{i=1}^m$ .定理1的证明 由文献[14]的定理B.1.9知,对x>1和t≥t0有,
则
令tx=Zj(i),t=Zj(d+1),由(8)式和(9)式知
由(10)式和(11)式可得
由文献[15]的引理3.4知
其中{Ej(i),i=1,…,d}服从独立同分布的标准指数分布,j=1,…,k. 因此
将(13)式及(14)式代入不等式(12)即可得
$\hat{\gamma}_{\mathrm{DMR}} \stackrel{P}{\longrightarrow} \gamma $ ,定理证毕.对定理2的证明,我们需要下面这个辅助引理.
引理1 令Z(1)≥…≥Z(m)表示服从Pareto(1)分布的独立随机变量{Z1,…,Zm}的次序统计量,则对任意ρ≤0,有
其中g(d,m,ρ)的定义见(2)式. 并且,当m→∞时,
证 见文献[13]的引理S.3.
定理2的证明 由文献[14]的定理B.2.18知,存在一个函数A0(t),使得当t→∞时,A0(t)~A(t),且对所有ε>0,δ>0,存在一个t0>0使得对tx≥t0,t≥t0,
定义
$\mathscr{S}_{n, d, t_0}=\left\{Z_j^{(d+1)} \geqslant t_0, 1 \leqslant j \leqslant k\right\} $ ,由文献[13]的引理S.2知,对任意t0>0,$ \lim\limits _{n \rightarrow \infty} \mathrm{P}\left(\mathscr{S}_{n, d, t_0}\right)=1$ . 所以,基于集合$ \mathscr{I}_{n, d, t_0}$ ,我们用$ \frac{m}{d}$ 和Zj(i),i=1,2,…,d+1替换不等式(15)中的t和tx,得到对i和i=d+1应用两次不等式(16),当n→∞时,
对ρ < 0,存在δ>0使得ρ+δ < 0,应用不等式
可以得到
与定理1的证明类似,我们可以得到当n→∞时,
$ I_1 \stackrel{d}{\longrightarrow} N\left(0, 2 \gamma^2\right)$ .对于I2,记
由弱大数定律可知,当n→∞时,
故
由引理1知,当m→∞时,
结合
$ (k d)^{\frac{1}{2}} A\left(\frac{m}{d}\right)=O(1)$ 的假设可以得到,当n→∞时,$I_2=\frac{2-\rho}{1-\rho}(k d)^{\frac{1}{2}} A_0\left(\frac{m}{d}\right) g(d, m, \rho)+o_p(1) $ . 类似地可以得到$I_3=-(k d)^{\frac{1}{2}} A_0\left(\frac{m}{d}\right) g(d, m, \rho)+o_p(1) $ . 故$I_2+I_3=\frac{1}{1-\rho}(k d)^{\frac{1}{2}} A_0\left(\frac{m}{d}\right) g(d, m, \rho)+ o_p(1)$ .与I2的计算类似,可以得到
$I_4 \stackrel{P}{\longrightarrow} 0, I_5 \stackrel{P}{\longrightarrow} 0 $ .综上,当n→∞时,
$(k d)^{\frac{1}{2}}\left\{\hat{\gamma}_{\mathrm{DMR}}-\gamma-(1-\rho)^{-1} A\left(\frac{m}{d}\right) g(d, m, \rho)\right\} \stackrel{d}{\longrightarrow} N\left(0, 2 \gamma^2\right) $ ,ρ < 0时的结论得证.对于ρ=0,(16)式等价于当n→∞时,
其后的证明方法与ρ < 0的情况类似,此处省略,定理证毕.
-
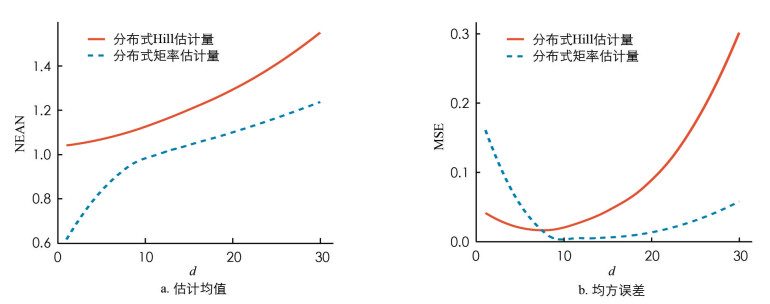
本文提出了分布式矩率估计量,下面将其与分布式Hill估计量进行有限样本表现的比较. 以γ=1,ρ=-1,机器数量一定时,Burr分布的表现为例,其分布函数为F(x)=1-(1+x)-1. 随机生成n个来自Burr分布的样本,存储在k个机器中,每个机器有m个观测,对每一个机器,从m个观测中选取d个超过数(d为自变量),分别计算分布式Hill估计量和分布式矩率估计量的估计均值和均方误差,每个实验重复s次并取平均值.
设置n=1 000,k=20,m=50,s=100,d的取值范围为1,…,30,模拟结果如图 1所示.
由图 1可知,当k一定时,在γ=1,ρ=-1的Burr分布下,随着d的增加,
$\hat{\gamma}_{\mathrm{DH}} $ 和$\hat{\gamma}_{\mathrm{DMR}} $ 的均值都存在上升的趋势,但当d较大时,$\hat{\gamma}_{\mathrm{DMR}} $ 的均值更接近真实值;同时,$\hat{\gamma}_{\mathrm{DH}} $ 和$\hat{\gamma}_{\mathrm{DMR}} $ 的均方误差随着d的增加先下降后上升,并且当d较大时,$\hat{\gamma}_{\mathrm{DMR}} $ 的均方误差低于$\hat{\gamma}_{\mathrm{DH}} $ 的均方误差,表现更为稳定. 因此,在最小均方误差准则下,当d较大时,$\hat{\gamma}_{\mathrm{DMR}} $ 的估计效果明显优于$\hat{\gamma}_{\mathrm{DH}} $ .



 下载:
下载: