本节从Jordan不等式、未定式极限和反常积分的收敛性等方面开展基于函数$\frac{{\sin x}}{x}$的高等数学教学探讨.

例1  设$x \in \left( {0, \frac{{\rm{ \mathsf{ π} }}}{2}} \right)$，则有$\frac{2}{{\rm{ \mathsf{ π} }}}x < \sin x < x$.

凹凸性是函数的一个重要性质，其应用很广^[6-7].例1直接与函数的凹凸性、单调性等知识点紧密相关，教学中可侧重向这些知识点引导.

Jordan不等式的几何含义是：由于正弦函数sin x在区间$\left( {0, \frac{{\rm{ \mathsf{ π} }}}{2}} \right)$上是上凸函数，故曲线sin x应位于它在原点处的切线下方，同时又位于连接(0，0)和$\left( {\frac{{\rm{ \mathsf{ π} }}}{2}, 1} \right)$这两点的弦的上方，如图 1.

借助于Jordan不等式，可以小结不等式的证明方法.以左边不等式$\frac{{2x}}{{\rm{ \mathsf{ π} }}}$ < sin x为例，可令

则有

由此不难得到f(x)在$\left( {0, \frac{{\rm{ \mathsf{ π} }}}{2}} \right)$上单调递减(图 2)，故所需结论得证.

另外，我们亦可令

利用分析函数g(x)的最小值来证明所需不等式.从不同角度分析同一个问题，可较好地帮助学生巩固所学的方法.

同时根据二阶导数

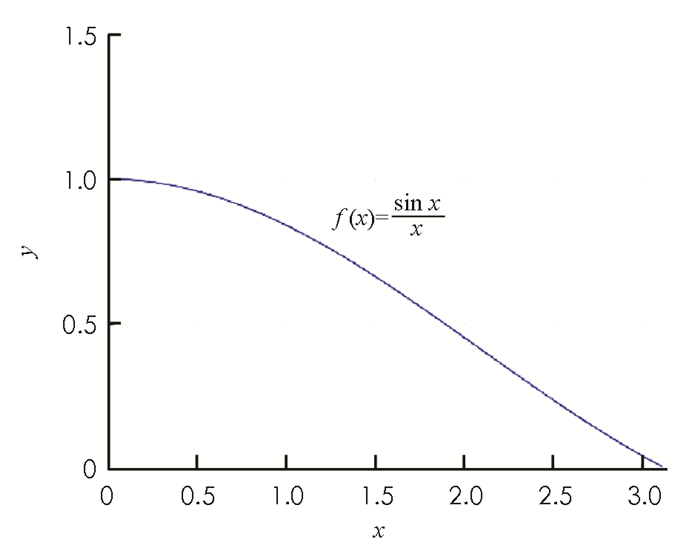
还可分析函数f的拐点分布情况，这归结为讨论方程$\tan x - \frac{{2x}}{{2 - {x^2}}} = 0$的根的分布，于是又可结合零点存在定理去讨论.这样就把前后的知识点贯穿起来，循序引导学生想象出该函数的大致图像.最后通过Matlab数学软件画出f(x)的函数图像(图 3)，将理论分析结果通过展现的图像从几何直观上进行验证.

进一步，在实践中可采用启发式教学，从图 1可以看出g(x)在$\left( {0, \frac{{\rm{ \mathsf{ π} }}}{2}} \right)$上是严格大于0的，因此是否可以将不等式sin x>$\frac{2}{{\rm{ \mathsf{ π} }}}x$改进到sin x>h(x)呢？这里的函数h(x)为满足条件h(0)=$h\left( {\frac{{\rm{ \mathsf{ π} }}}{2}} \right)$=0的高次多项式，这就涉及到Jordan不等式的改进^[8-10]，为感兴趣的同学留下了进一步探讨的空间.

众所周知，有重要极限limx→0$\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1$=1.基于此，教学中可构造许多相关求极限的例子.

例2设α>0，试分析极限$\mathop {\lim }\limits_{x \to {0^ + }} {\left( {\frac{{\sin x}}{x}} \right)^{\frac{1}{{{x^a}}}}}$.

解法1  运用洛必达法则和等价无穷小替换原理，有

易见

解法2  由于

利用泰勒公式，有

由此不难得到解法1中的结果.

例2的极限是1^∞-型形式，上述结果(极限值依赖于参数α)让学生进一步体会了未定式极限的含义，更重要的是在极限求解过程中运用了洛必达法则、等价无穷小替换、重要极限、泰勒公式等理论，可较好地对已学知识点进行巩固和理解.

下面一例是北京大学2018年硕士研究生入学考试数学分析科目中的一道题，实际教学中可以通过各种形式灵活设计成供学生练习提高的题目.

例3  试证明$\mathop {\lim }\limits_{n \to \infty } {\left( {1 + \int {_0^1\frac{{{{\sin }^n}x}}{{{x^n}}}{\rm{d}}x} } \right)^n} = + \infty $.

注意，对任意充分小的ε>0，有

对此固定的ε，有0 < $\frac{{\sin \varepsilon }}{\varepsilon }$ < 1，故可取n充分大，使得${\left( {\frac{{\sin \varepsilon }}{\varepsilon }} \right)^n} < \varepsilon $，由此可得

因此上述极限也是1^∞-型未定式.

证  要证明所需结论，等价于证明

也等价于

利用$\frac{{\sin x}}{x}$的单调递减性质，有

现取$\delta = \frac{1}{{\sqrt n }}$，根据例2的结果可得

由此立即可证明出所需结论.

当然以上证明方法并非是唯一的，可鼓励学生积极探索其它方法.

例4  试分析反常积分$\int {_0^{ + \infty }} \frac{{\sin x}}{x}{\rm{d}}x$的敛散性.

这是条件收敛的一个经典例子.证明加绝对值发散时，利用了不等式^[11-12]

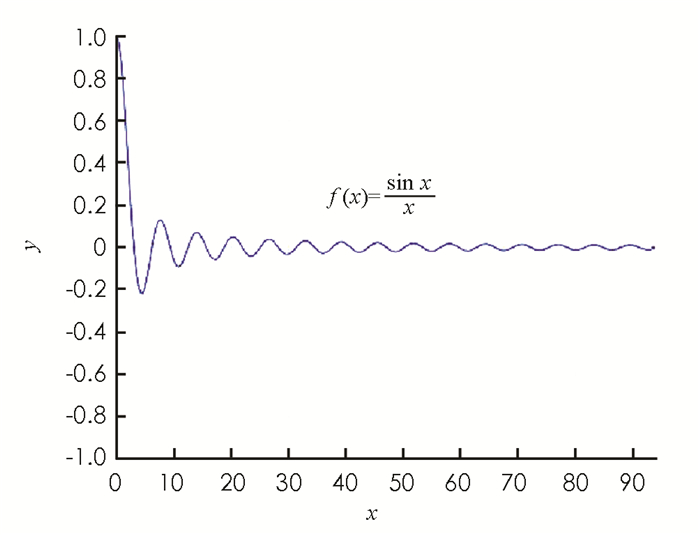
在教学中，可结合几何图形加以讲解.由于

在区间(nπ，(n+1)π)上，可考虑(nπ，0)，$\left( {n{\rm{ \mathsf{ π} }} + \frac{{\rm{ \mathsf{ π} }}}{{\rm{2}}}, 0} \right)$和$\left( {n{\rm{ \mathsf{ π} }} + \frac{{\rm{ \mathsf{ π} }}}{{\rm{2}}}, {{\left( {n{\rm{ \mathsf{ π} }} + \frac{{\rm{ \mathsf{ π} }}}{{\rm{2}}}} \right)}^{ - 1}}} \right)$这三点围成的直角三角形面积，根据前述的几何图形，易见

由此可得积分$\int {_0^{ + \infty }} \frac{{\left| {\sin x} \right|}}{x}{\rm{d}}x$是发散的.

为说明原积分的收敛性，除用Dirichlet判别法外，也可借助于图形进行讲授.对充分大的0 < A₁ < A₂，存在正整数k，l，满足

设l>k，且无妨设：在(kπ，(k+1)π)上sin x>0(即k为偶数)；在(lπ，(l+1)π)上sin x < 0(即l为奇数).其它情形可类似分析.于是有

其中

对于I₂，通过平移变换，有

联合以上估计，得

再结合Cauchy收敛准则即可证明原反常积分收敛.上述直接分析方式法看似繁琐，但却是一种较为直观的处理办法，学生易于接受，同时也温习了Cauchy收敛准则，可以更深层次理解Dirichlet判别法的应用价值.得到该积分的收敛性之后，也为后续Dirichlet积分的计算作了铺垫.

本文对高等数学中的重要函数$\frac{{\sin x}}{x}$的教学进行了探索，通过精心选择和设计与之相关的例子，在极限论、微分学、积分学、级数理论等模块都结合该函数展开了相关知识点的探讨，由浅入深，环环相扣.利用启发式教学、探究式教学等多种手段并结合数学软件讲深讲透，提高了学生学习的兴趣和积极主动性.通过本文的讨论，希望可起到抛砖引玉的作用，将该类函数及其诸多变形贯穿于整个高等数学教学体系的始终，循序引导，激发学生的数学潜力，提高高等数学教学质量.