-
亥姆霍兹线圈是一对彼此平行且连通的共轴圆形线圈,两线圈的电流方向一致,大小相同,线圈之间的距离d正好等于圆形线圈的半径R.亥姆霍兹线圈的特点是能在公共轴线中间附近产生较广的均匀磁场区,且操作空间大,适合做大尺寸均匀磁场发生器,所以在科研、工业和医学等领域中有较大的使用价值,可完成地球磁场的补偿、生物磁场的研究,也常用于弱磁场的计量标准[1-4].
关于亥姆霍兹线圈磁场分布的理论分析与计算,已有部分研究结果,如文献[5]采用泰勒级数展开的方式处理,但只取了前4项,并不能精确反映空间所有区域磁场分布;文献[6]讨论了亥姆霍兹线圈轴线上的磁感分布,并结合实验做了对比分析,但并没有讨论空间所有点的磁场分布;文献[7]利用Mathematica软件对亥姆霍兹线圈磁场分布做了数值模拟;此外,文献[8]讨论了载流圆线圈电流平面内的磁场分布,并给出了以椭圆积分表示的结果;等等.亥姆霍兹线圈磁场的测量也是大学物理实验中十分重要的电磁学实验,测量方法主要有“霍耳效应法测量亥姆霍兹线圈磁场”和“电磁感应法测量亥姆霍兹磁场”两种.其中“电磁感应法测量亥姆霍兹磁场”是利用给亥姆霍兹线圈加上交变电流,线圈产生交变磁场并穿过一个小感应线圈,通过测量感应线圈的感应电动势来测量亥姆霍兹线圈中心轴线上的磁场.在测量中有这样一个假设,认为穿过小线圈的磁场是均匀的,这样的处理是否合理?同学们在实验中往往有此疑惑.
本研究首先从理论上计算了亥姆霍兹线圈的磁感强度.基于毕奥—萨尔定律,分析了单个载流圆线圈在空间磁场分布的积分表达式,对于磁感强度的解析结果,本研究给出了两种处理方式:一种方式是通过泰勒级数将被积函数展开,通过计算最终得到一个无穷级数求和的解析表达式;另一种方式是直接借助于Mathematica软件做解析计算,积分结果由超几何函数表示.再将单个载流圆线圈在空间激发的磁场推广到亥姆霍兹线圈,得到了亥姆霍兹线圈磁场在全空间分布的解析结果,并利用Mathematica软件中的StreamPlot命令形象描绘了亥姆霍兹线圈在空间的磁感线分布.相对于文献[5-8],本研究给出了全空间磁场分布的级数表达式的所有阶结果,并通过Mathematica形象描绘了磁感线分布以及磁场轴向分量和径向分量在空间的分布.此外,本研究通过数值计算给出了磁感应强度轴向分布和经向分布的数值结果,数值结果显示在亥姆霍兹线圈中心轴线附近较大区域存在一个均匀磁场.最后,结合“电磁感应法测量亥姆霍兹线圈磁场”实验,通过具体数值结果讨论了将亥姆霍兹线圈激发的磁场穿过小线圈的区域看作“均匀磁场”的合理性.
全文HTML
-
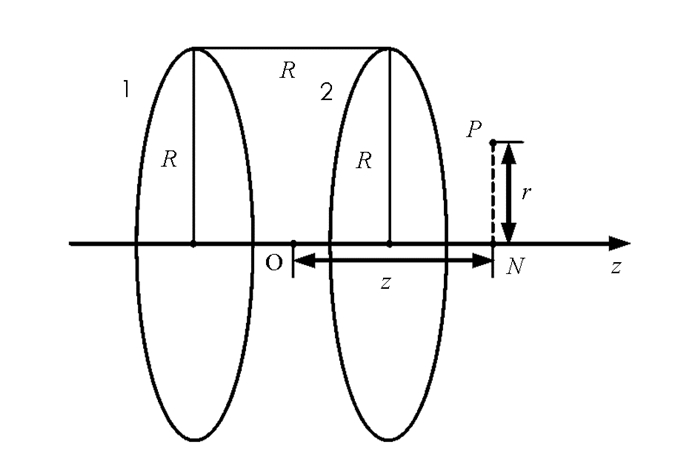
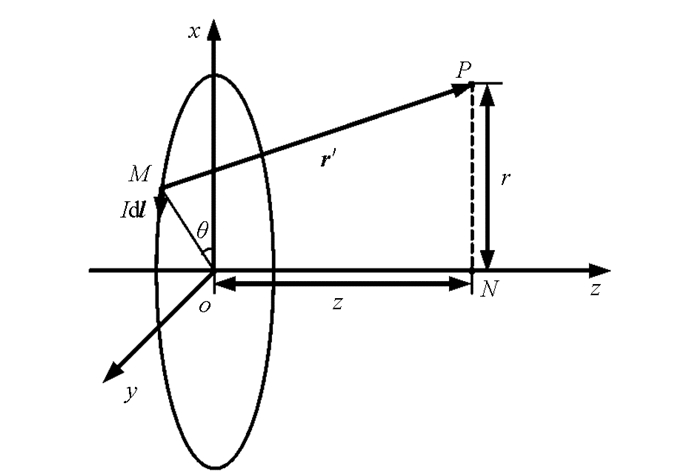
首先利用毕奥一萨尔定律和矢量叉乘运算推导单个载流圆线圈在空间的磁感强度分布,再推广到亥姆霍兹线圈在空间的磁感分布.设空间一点P到载流圆线圈中心轴线z轴的距离为r,P在z轴上的投影点距离o为z(图 1).
根据几何关系可得,r′=(r-Rcosθ)i-Rsinθj+zk,dl=Rdθ(cosθj-sinθi),因而
根据毕奥—萨尔定律dB=μ0Idl×r′/4πr′3,并对角度积分可得
根据函数奇偶性分析可得By=0,即载流圆线圈在空间的磁场分布只沿轴向(z方向)及径向有分布,因而可将(2)式中的Bx理解为沿径向分布Br.上述Bx和Bz的积分十分复杂,原函数已不能用初等解析函数表示出来.令k=2Rr/(z2+R2+r2),可将(2)式化成
将(1-kcosθ)-3/2用泰勒级数展开,进而可将Br表示成
对(6)式中关于cosn+1θ的积分,采用分部积分法,可得
将(7)式代入(6)式可得载流圆线圈磁场的径向分布
经过同样的处理,也可得到P点磁感强度沿轴向分量为
(9) 式中k取4时便是文献[5]的结果,但当k值接近于1时,(8)式和(9)式中级数收敛较慢,只取前几项时会带来较大误差.此外,也可直接借助于Mathematica对(2)式和(4)式做解析积分,结果为
式中,z1=-4rR/[z2+(R-r)2],z2=4rR/[z2+(R+r)2];2F1(a,b;c;z)为超几何函数[9]:
其中q(n)是Pochhammer符号,定义为:
现有一亥姆霍兹线圈,半径为R,通有电流I,线圈之间的而距离d=R(图 2).
空间一点P到亥姆霍兹线圈中心轴线z轴的距离为r,P在z轴上的投影点距离坐标原点为z,则P点到线圈1的垂直距离为z+R/2,到线圈2的垂直距离为z-R/2.只要将单个载流圆线圈的磁场分别沿z轴向左、向右平移R/2即可得到图 2中两个线圈各自产生的磁场;将它们叠加起来便得到亥姆霍兹线圈的磁场.
基于(8)式和(9)式的结果,可得P点的磁感应强度为
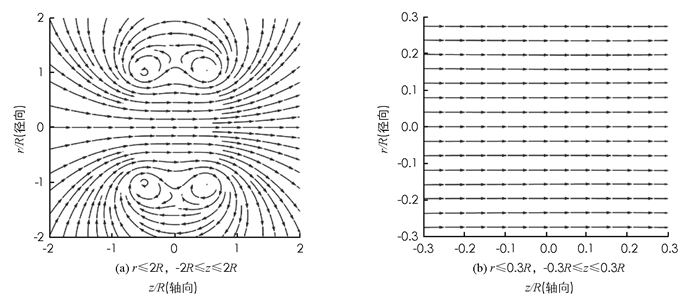
其中,k1=2Rr/[(z+R/2)2+R2+r2],k2=2Rr/[(z-R/2)2+R2+r2].从(16)和(17)式也可以看出径向磁感强度是奇函数Br(r,-z)=-Br(r,z),轴向磁感强度是偶函数Bz(r,-z)=Bz(r,z). 图 3利用Mathematica中的StreamPlot命令形象地描绘了亥姆霍兹磁感线圈磁感线分布沿中心轴线的剖面图,其中将线圈半径R取为1,将系数μ0IR/4π也取为1.在Mathematica中输入如下命令:
便可的到图 3(a)所示的磁感线分布示意图(图中磁感线的密疏表示磁场的强弱). 图 3(b)是将磁感线区域定为从r≤0.3R和-0.3R≤z≤0.3R区域,图 3(b)可以看出在亥姆霍兹线圈中心轴线附近有一个均匀磁场区.
-
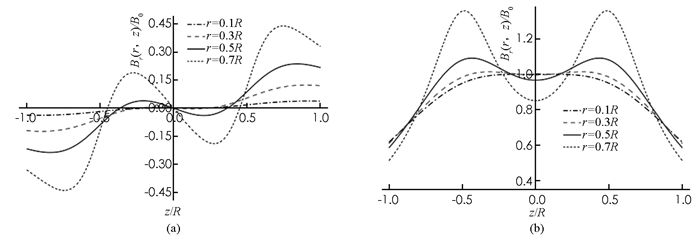
为了定量分析亥姆霍兹线圈在空间的磁场分布,表 1和表 2分别给出了亥姆霍兹线圈沿轴径和径向的磁感应强度分布随R和z的变化;图 4给出了亥姆霍兹线圈磁感应强度沿轴向分布.
从表 1、表 2和图 4中可以看出:在亥姆霍兹线圈中心轴上以中心点O为中心,以0.3R为半径,以0.6R为长的圆柱形区域内(公共轴线附近区域),磁感应强度沿轴向分布Bz与中心处磁感应强度B0相比,改变率不超过1.39%,磁感应强度沿径向分布Br的大小不超过B0的1%,这个区域认为是均场强磁场是合理的;在较远区域(0.3R≤r≤0.5R),Bz缓慢增加,Br也开始增加,磁场不再是均匀分布;在很远区域(r>0.5R), Bz迅速变化,Br也增加较快,磁场完全不能看作均匀磁场.
-
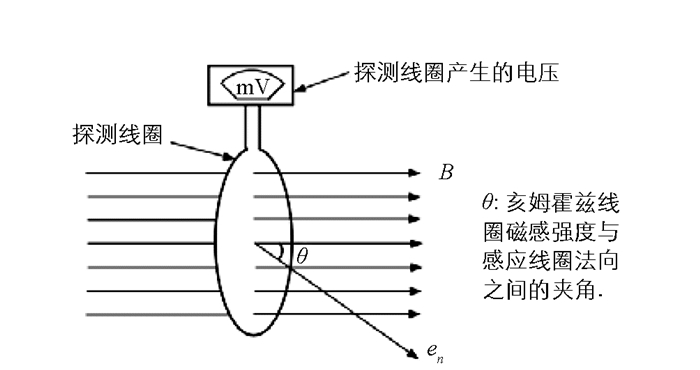
“亥姆霍兹线圈磁场测量”是大学物理中一个重要的必修实验,测量方法主要有“霍尔效应法”[10]和“电磁感应法”[10]两种.本文针对“电磁感应法测量亥姆霍兹线圈磁场”的实验进行理论分析,实验仪器采用杭州大华仪器制造公司生产的DH4501型亥姆霍兹磁场测量仪.该仪器中亥姆霍兹线圈有效半径R=105 mm;探测线圈和亥姆霍兹线圈共轴,且可以沿径向移动,探测线圈外径D=12 mm(探测线圈的外径约亥姆霍兹线圈半径的0.057倍),线圈等效面积S=13πD2/108.在实验中认为穿过探测线圈的磁场是均匀磁场,磁感强度大小等于线圈中心点的磁感强度(图 5).在实验中同学们往往有如下的疑问:实验中沿亥姆霍兹线圈轴线测量的范围是-R~R.在此范围内,磁感应强度是否满足关系式∫SB·ds=B0S,要说明此问题,就要知道磁感强度在r≤0.057R,Z∈(-R,R)范围内的分布情况. 表 3和表 4分别给出了Bz(r,z)和Br(r,z)在此区域的磁感强度分布,由表 3可以看出Bz(r,z)的相对变化率
$\varepsilon = \frac{{{B_z}\left( {0.06R, z} \right){B_z}\left( {0, z} \right)}}{{{B_z}\left( {0, z} \right)}}$ 很小,不超过0.15%.但随着Z和r的增加,$\frac{{{B_r}\left( {r, z} \right)}}{{{B_z}\left( {r, z} \right)}}$ 逐渐增加,最大值$\frac{{{B_r}\left( {0.06R, 1.0R} \right)}}{{{B_z}\left( {0.06R, 1.0R} \right)}}$ 可达到0.037 2.由于线圈的法向沿着轴向(z方向),穿过磁感应线圈的磁通量∫SB·ds=∫S(Bzk+Brr)·dsk=∫SBzds,因而B的径向分量Br对Φm无影响,因而认为穿过探测线圈的磁场是均匀磁场是完全合理的,但也说明在实验过程中应使感应线圈的法向沿着轴向,否则会带来实验误差.
-
本研究基于毕奥-萨尔定律,首先分析了单个载流圆线圈在空间的磁场分布,进而推广到亥姆霍兹线圈,并通过两种方法得到了亥姆霍兹线圈在空间任意一点磁感强度的解析结果,还通过数值结果具体讨论了亥姆霍兹线圈在空间产生B的均匀区.此外,本研究还通过Mathematica软件形象描绘了亥姆霍兹线圈在空间的磁感线分布.最后,本文结合“电磁感应法测量亥姆霍兹线圈磁场”实验,具体讨论了该实验处理方式的合理性.
由于亥姆霍兹线圈的广泛应用,在大学物理和大学物理实验课堂中,可适当增加关于亥姆霍兹线圈在全空间磁场分布的讨论,一方面可以提高学生分析问题的能力,理解亥姆霍兹线圈产生均匀磁场区域的原因,另一方面也可使学生在做相关实验时减少疑问与困惑.



 下载:
下载: