高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

分数阶简化Lorenz系统的FPGA实现

,  , 

上一篇

下一篇

周围, 王强, 吴周青. 分数阶简化Lorenz系统的FPGA实现[J]. 西南大学学报（自然科学版）, 2020, 42(7): 177-183. doi: 10.13718/j.cnki.xdzk.2020.07.018
引用本文: 周围, 王强, 吴周青. 分数阶简化Lorenz系统的FPGA实现[J]. 西南大学学报（自然科学版）, 2020, 42(7): 177-183. doi: 10.13718/j.cnki.xdzk.2020.07.018
shu
Wei ZHOU, Qiang WANG, Zhou-qing WU. FPGA Implementation of the Fractional-Order Simplified Lorenz System[J]. Journal of Southwest University Natural Science Edition, 2020, 42(7): 177-183. doi: 10.13718/j.cnki.xdzk.2020.07.018
Citation: Wei ZHOU, Qiang WANG, Zhou-qing WU. FPGA Implementation of the Fractional-Order Simplified Lorenz System[J]. Journal of Southwest University Natural Science Edition, 2020, 42(7): 177-183. doi: 10.13718/j.cnki.xdzk.2020.07.018
shu

分数阶简化Lorenz系统的FPGA实现

  • 1.

    重庆邮电大学 光电工程学院/重庆国际半导体学院，重庆 400065

  • 2.

    重庆邮电大学 移动通信技术重庆市重点实验室，重庆 400065

  • 基金项目: 国家自然科学基金项目(61771085)；重庆市基础与前沿研究计划项目(CSTC2015icyjA40040)
详细信息
    作者简介:

    周围(1971-)，男，博士，教授，主要从事非线性电路与系统、通信系统及信号处理研究 .

  • 中图分类号: TN914

FPGA Implementation of the Fractional-Order Simplified Lorenz System

  • 1.

    College of Electronics Engineering/International Semiconductor College, Chongqing University of Posts and Telecommunications, Chongqing 400065, China

  • 2.

    Chongqing Key Laboratory of Mobile Communications Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, China

  • 摘要: 目前针对分数阶混沌系统的研究大多数都是基于DSP(Digital Signal Processor)平台，由于分数阶混沌系统的复杂度较大，用DSP实现存在序列生成速度较慢的问题，只能应用于对速度要求不高的系统.针对该问题，研究了基于分数阶微积分Grunwald-Letnikov(GL)定义的分数阶简化Lorenz系统的FPGA(field programmable gate array)实现.通过最大Lyapunov指数和0~1测试验证了基于GL定义的分数阶简化Lorenz系统是混沌的.详细分析了基于GL定义的分数阶简化Lorenz系统的FPGA实现结构，并使用定点数格式实现了该系统.通过示波器观察FPGA输出结果与MATLAB仿真结果一致，从而进一步揭示了分数阶混沌系统的可实现性.
    Abstract: At present, most of the researches on fractional-order chaotic systems are based on the DSP platform. However, due to the complexity of fractional-order chaotic systems, the implementation of DSP has the problem of slow sequence generation, so that it can only be applied to low-speed systems. To solve this problem, an FPGA (field programmable gate array) implementation of fractional-order simplified Lorenz system based on the definition of fractional-order differential Grunwald-Letnikov (GL) is studied and developed. Firstly, it is verified through the maximum Lyapunov exponent and the 0-1 test that the fractional-order simplified Lorenz system based on the GL definition is chaotic. Then, the FPGA implementation structure of the fractional-order simplified Lorenz system based on GL definition is analyzed in detail, and the system is implemented using a fixed-point number format. Finally, the FPGA output results observed through an oscilloscope are shown to be consistent with MATLAB simulation results, which further reveals the feasibility of the fractional-order chaotic system.
  • 加载中

  • 图 1  a=5，q=0.98时，系统(2)产生的混沌吸引子

    下载: 全尺寸图片 幻灯片

    图 2  系统(2)的最大Lyapunov指数谱(a=5)

    下载: 全尺寸图片 幻灯片

    图 3  q变化时系统(2)的异步增长率(a=5)

    下载: 全尺寸图片 幻灯片

    图 4  分数阶Lorenz混沌系统的FPGA结构图

    下载: 全尺寸图片 幻灯片

    图 5  MUL_ACC_PART模块的FPGA结构图

    下载: 全尺寸图片 幻灯片

    图 6  示波器捕捉的混沌吸引子相图

    下载: 全尺寸图片 幻灯片
  • [1] PODLUBNY I. Fractional Differential Equation [M]. New York: Academic Press, 1999.
    [2] MANDELBRT B B. The Fractal Geometry of Nature [M]. New York: Freeman, 1983.
    [3] 贾红艳, 陈增强, 薛薇.分数阶Lorenz系统的分析及电路实现[J].物理学报, 2013, 62(14): 48-54. doi: http://d.old.wanfangdata.com.cn/Periodical/wlxb201314008
    [4] 陈向荣, 刘崇新, 王发强, 等.分数阶Liu混沌系统及其电路实验的研究与控制[J].物理学报, 2008, 57(3): 1416-1422. doi: http://d.old.wanfangdata.com.cn/Periodical/wlxb200803023
    [5] 陈恒, 雷腾飞, 王震, 等.分数阶Chen混沌系统的动力学分析与电路实现[J].河北师范大学学报(自然科学版), 2015, 39(3): 208-215. doi: http://www.cnki.com.cn/Article/CJFDTotal-HBSZ201503006.htm
    [6] doi: https://link.springer.com/article/10.1007/s11042-017-5439-6 ANNABY M H, AYAD H, RUSHDI M A. On Security of Image CiphersBased on Logic Circuits and Chaotic Permutations [J]. Multimedia Tools and Applications, 2018, 77(16): 20455-20476.
    [7] 毛骁骁, 孙克辉, 刘文浩.基于分数阶统一混沌系统的图像加密算法[J].传感器与微系统, 2017, 36(6): 138-141. doi: http://d.old.wanfangdata.com.cn/Periodical/cgqjs201706039
    [8] 周平, 危丽佳, 程雪峰.一个分数阶混沌系统及其EWB仿真结果[J].西南大学学报(自然科学版), 2009, 31(1): 69-74. doi: http://xbgjxt.swu.edu.cn/article/id/jsunsxnnydxxb200901016
    [9] doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=968471a3625940541cc0ac98ad7d08ff ATAN O. Implementation and Simulation of Fractional Order Chaotic Circuits with Time-Delay [J]. Analog Integrated Circuitsand Signal Processing, 2018, 96(3): 485-494.
    [10] doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=MDPI000000094695 HE S B, SUN K H, WANG H H. Complexity Analysis and DSP Implementation of the Fractional-Order Lorenz Hyperchaotic System [J]. Entropy, 2015, 17(12): 8299-8311.
    [11] 雷腾飞, 王艳玲, 苏敏, 等.分数阶Qi混沌系统的动力学分析及DSP实现[J].温州大学学报(自然科学版), 2018, 39(1): 32-39. doi: http://d.old.wanfangdata.com.cn/Periodical/wzsfxyxb201801007
    [12] doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1142/S0218127402006230 ZHONG G Q, MAN K F, CHEN G R. A Systematic Approach to Generating N-scroll Attractors [J]. International Journal of Bifurcation and Chaos, 2002, 12(12): 2907-2915.
    [13] doi: https://core.ac.uk/download/pdf/102067.pdf GOTTWALD G A, MELBOURNE I. ANew Test for Chaos in Deterministic Systems [J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 2004, 460(2042): 603-611.
    [14] doi: http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_nlin%2f0410020 GOTTWALD G A, MELBOURNE I. Testing for Chaos in Deterministic Systems with Noise [J]. Physica D Nonlinear Phenomena, 2004, 212(1): 100-110.
  • 加载中
图( 6)
计量
  • 文章访问数:  1051
  • HTML全文浏览数:  1051
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2018-09-11
  • 刊出日期:  2020-07-01

分数阶简化Lorenz系统的FPGA实现

    作者简介: 周围(1971-)，男，博士，教授，主要从事非线性电路与系统、通信系统及信号处理研究
  • 1. 重庆邮电大学 光电工程学院/重庆国际半导体学院，重庆 400065
  • 2. 重庆邮电大学 移动通信技术重庆市重点实验室，重庆 400065
  • 收稿日期:  2018-09-11
基金项目:  国家自然科学基金项目(61771085)；重庆市基础与前沿研究计划项目(CSTC2015icyjA40040)

摘要: 目前针对分数阶混沌系统的研究大多数都是基于DSP(Digital Signal Processor)平台，由于分数阶混沌系统的复杂度较大，用DSP实现存在序列生成速度较慢的问题，只能应用于对速度要求不高的系统.针对该问题，研究了基于分数阶微积分Grunwald-Letnikov(GL)定义的分数阶简化Lorenz系统的FPGA(field programmable gate array)实现.通过最大Lyapunov指数和0~1测试验证了基于GL定义的分数阶简化Lorenz系统是混沌的.详细分析了基于GL定义的分数阶简化Lorenz系统的FPGA实现结构，并使用定点数格式实现了该系统.通过示波器观察FPGA输出结果与MATLAB仿真结果一致，从而进一步揭示了分数阶混沌系统的可实现性.

English Abstract

    全文HTML

  • 分数阶微积分与牛顿莱布尼茨整数阶微积分几乎是同时代被提出，最早可以追溯到Leibniz和Newton提出微积分学的时代，至今已经有300多年的历史.由于当时社会条件的限制，分数阶微积分在相当长的一段时间内并没有取得较显著的成果[1].近几十年来，随着非线性动力学理论的发展，混沌动力学理论的研究也随之发展和完善，从而使得分数阶混沌系统的探讨与研究已成为新的研究领域[2].在分数阶混沌系统的研究中，主要是在经典的混沌系统基础上，引入分数阶微积分算子，如分数阶Lorenz系统[3]、分数阶Liu系统[4]、分数阶Chen系统[5]等.

    混沌系统具有伪随机性、初值敏感性等特征，非常适合应用于密码学领域[6].分数阶混沌系统在混沌系统的基础上，由于具有记忆性，产生的序列伪随机特性更好，在密码学领域与混沌系统相比具有更大的优势[7].电路的实现是分数阶混沌系统应用的基础，目前的实现方法主要有2种：①模拟电路[8-9]，②数字电路[10-11].模拟电路由于易受环境、器件老化等影响且电路参数离散性较大、通用性差，从而限制了它的实际应用[12].而数字电路可以很好地解决模拟电路的这些问题.目前，分数阶混沌系统的数字电路实现大多数用DSP实现[10-11]，但是由于分数阶混沌系统的复杂度较大，用DSP实现序列的生成速度较慢，只能应用于对速度要求不高的系统. FPGA具有速度快、并行处理等特性，为了提高分数阶混沌系统的性能，可以用FPGA实现.

    分数阶微积分的定义有多种，Grunwald-Letnikov(GL)定义，一次迭代计算没有子迭代过程，并行度较高，非常适合用FPGA实现.本文以分数阶简化Lorenz混沌系统为研究对象，采用GL定义离散化系统，先通过最大Lyapunov指数和0~1测试验证了系统的阶数为分数时系统是混沌状态，然后详细介绍了分数阶混沌系统的FPGA实现.

1.   分数阶简化Lorenz混沌系统

  • 分数阶简化Lorenz混沌系统如系统(1)

    利用分数阶微积分GL定义和短记忆规则，系统(1)可写为离散形式，如系统(2)

    其中，a为系统参数，h为系统离散化取样时间，h=0.001 s，q是系统分数阶阶数，L是短记忆长度，Cj(α)为二项式系数，其迭代公式为

    短记忆规则的长度L可以通过式(4)确定，

    其中，M是系统状态变量的最大值，ε是采用短记忆规则后产生的误差，Γ(·)是gamma函数.式(4)中的M由MATLAB仿真可得，M=20，当误差ε=0.008时，根据式(4)，可得L近似值为60.

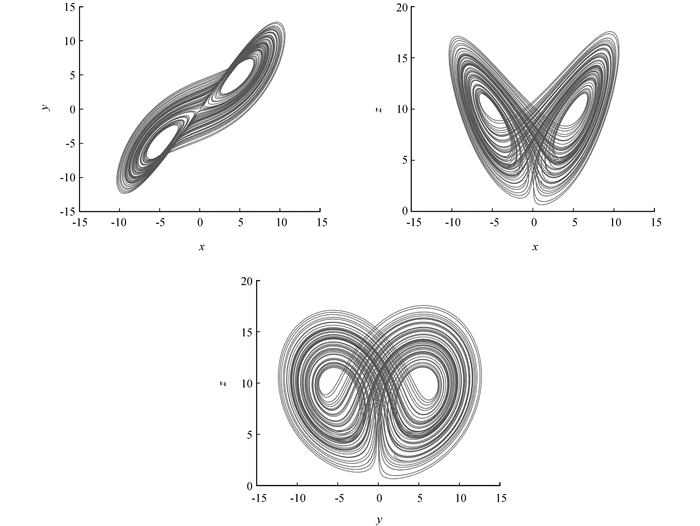
    当初值为[1, 2, 3]，a=5，q=0.98时，分数阶Lorenz混沌系统最大Lyapunov指数为0.9，最大Lyapunov指数大于零，所以此时系统是混沌的，其吸引子相图如图 1所示.

2.   最大Lyapunov指数和0~1测试

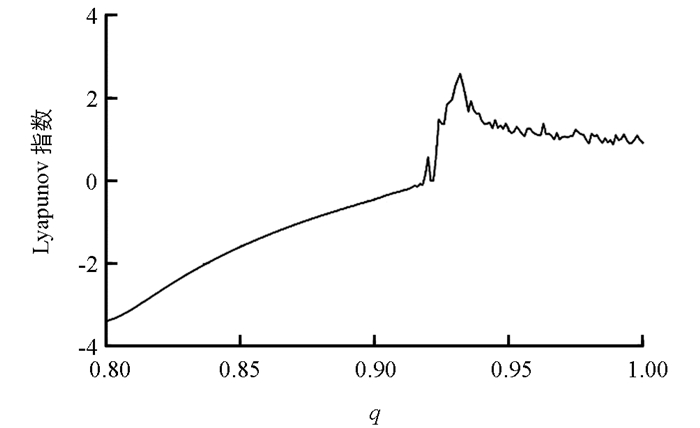
  • 为了验证系统(2)是混沌系统，可以通过MATLAB仿真求该系统的最大Lyapunov指数来验证.当初值为[1, 2, 3]，a=5时，系统(2)随分数阶阶数q变化的最大Lyapunov指数谱如图 2所示.从图 2可知，当q∈(0.92，1.00]时，系统最大Lyapunov指数大于零，表明此时系统为混沌状态.

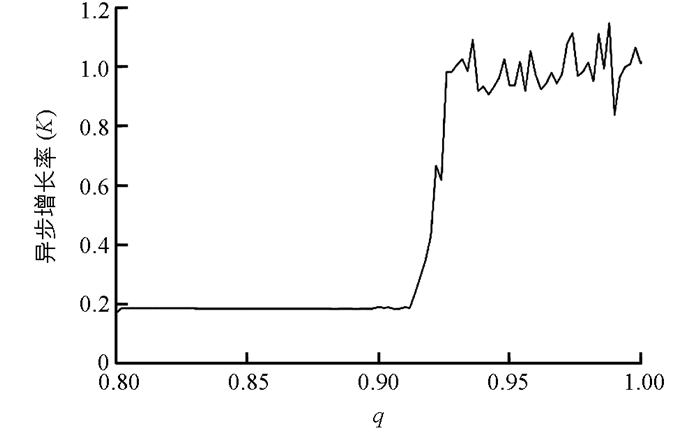
    文献[13]和文献[14]提出了另一种可靠且有效的检验系统是否为混沌的二进制测试方法，称为“0~1测试”，基本思想是为数据建立一个随机动态过程，然后研究该随机过程的规模是如何随着时间推移而变化的.该方法最后是求得数据的异步增长率K，当K接近于0时，运动是规则的(周期的或伪周期的)；当K接近于1时，运动是混沌的.利用该方法对分数阶简化Lorenz系统产生的序列进行研究，当初值为[1, 2, 3]，a=5时，系统(2)随分数阶阶数q变化的异步增长率如图 3所示.从图 3可知，当q∈(0.92，1.00]时，K接近1，为混沌状态，进一步证明了系统在q∈(0.92，1.00]时是混沌的.

3.   分数阶简化Lorenz系统的FPGA实现

  • 根据系统(2)可以算出分数阶简化Lorenz系统在记忆长度L=60时，进行一次迭代运算需要187次乘法运算和184次加减法运算，计算复杂度非常大.如果用一般的微处理器，由于不具有并行性，产生一个数据输出的延时较大，系统性能不高，不适合速度较高的应用场合. FPGA是一种半定制专用集成电路，内部具有丰富的逻辑资源，可以实现真正的并行性.每个独立的处理任务都配有专用的芯片部分，能在不受其他逻辑块的影响下自主运作，添加更多处理任务时不会影响其他应用性能，非常适合复杂数字系统的实现.因此FPGA非常适合分数阶简化Lorenz系统的实现.

    在FPGA中数据格式有浮点格式和定点格式2种.浮点格式的计算精度高于定点格式，不会有数据溢出，但是消耗的FPGA资源远远大于定点格式，并且一次计算需要几个时钟周期；而定点格式的计算一个时钟周期就可以完成.所以，在工程中往往采用定点格式.

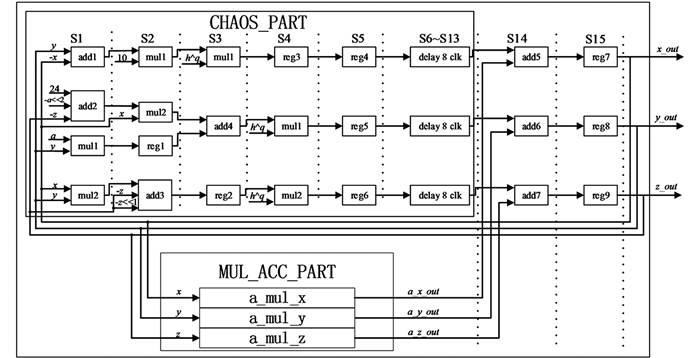
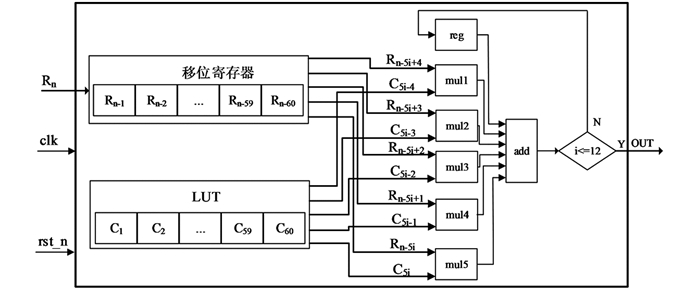
    分数阶简化Lorenz系统的FPGA结构如图 4所示，其中“≪”表示左移，add1-add7为定点数加法运算单元，mul1和mul2为定点数乘法运算知识产权(Intellectual Property，IP)核，reg1-reg9为寄存器.本文中定点数的位宽为35 bit，整数部分为15 bit，小数部分为20 bit. FPGA模块简图主要分为CHAOS_PART和MUL_ACC_PART两个模块，CHAOS_PART计算分数阶简化Lorenz混沌系统的$[10(y(n) - x(n))]{h^q}, [(24 - 4a)x(n) - x(n)z(n) + ay(n)]{h^q}{\rm{和}}[x(n)y(n) - 3z(n)]{h^q}$部分，MUL_ACC_PART计算分数阶简化Lorenz系统的$\sum\limits_{j = 1}^L {C_j^q} x(n - j), \sum\limits_{j = 1}^L {C_j^q} y(n - j){\rm{和}}\sum\limits_{j = 1}^L {C_j^q} z(n - j)$部分.整个模块的实现需要5个always块，一个always块进行状态机状态的转移，一个always块实现CHAOS_PART模块，另外3个always块实现MUL_ACC_PART模块. MUL_ACC_PART模块的a_mul_x，a_mul_y和a_mul_z分别对应一个always块，并且具有相同的结构.状态机总共有15个状态，分别是S1-S15. 图 4中虚线分隔的区域对应每个状态处理的任务，CHAOS_PART模块的计算实际上在S5状态时就已经完成，但是MUL_ACC_PART模块需要13个状态才能完成，所以CHAOS_PART模块需要等待8个状态才能保证时序上对齐，使计算正确.由于CHAOS_PART模块计算时间较充裕，为了减少硬件开销，只使用2个乘法器IP核，分时复用.

    MUL_ACC_PART模块的FPGA结构如图 5所示，该模块由移位寄存器、查找表(Look up Table，LUT)和乘累加器3个部分组成.由于记忆长度L=60，所以移位寄存器和LUT的长度都为60.移位寄存器每一个寄存器的宽度为35 bit，状态机每执行1次，移位寄存器右移1次，即移入最新的计算结果，移出最老的数据. LUT存储的是式(2)的二项式系数，为常数.乘累加器由5个乘法器IP核组成，分时复用，i表示第几个状态，每一个状态从移位寄存器和LUT中取出5个数进行计算，若没有到S12状态，则将计算的和保存到寄存器用于下一次计算求和，S13状态计算最后一次的和并且输出计算结果. S14状态计算CHAOS_PART和MUL_ACC_PART输出的和；S15状态缓存结果，并且将结果回传，用于下一次计算.

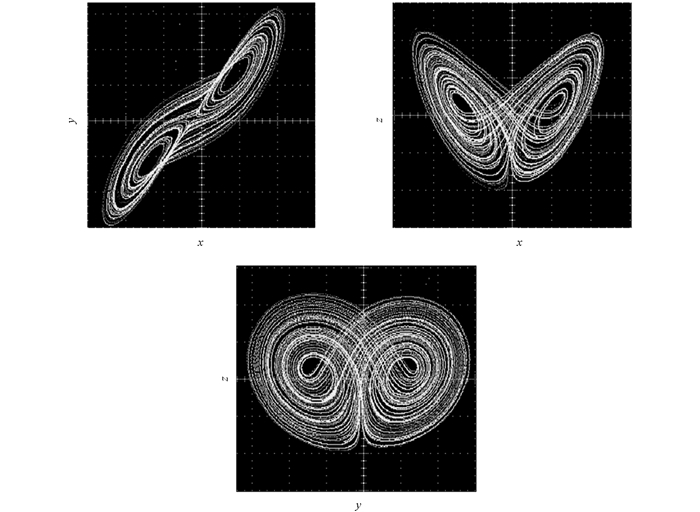
    实验用的FPGA开发板的芯片为Xilinx公司生产的，型号为xc7z020clg400.由于FPGA输出为数字信号，为了用示波器观察实验输出，需要通过数模转换器将数字信号转换为模拟信号.数模转换器型号为AD9767，是一款双口并行最高转换速率为125 MHz的数模转换器.开发软件为VIVADO，根据图 4和图 5用VERILOG硬件编程语言编写程序，编译成功后将生成的bin文件下载到FPGA内，通过数模转换器获得连续的模拟信号，使用型号为DPO4102B-L的示波器捕捉到分数阶简化Lorenz系统的混沌相图如图 6所示，实验结果与MATLAB的仿真结果一致，表明该系统可实现.

4.   结语

  • 本文利用GL定义和短记忆规则，先通过MATLAB仿真分析了分数阶简化Lorenz系统的相图和最大Lyapunov指数，并且进行了0~1测试.最大Lyapunov指数和0~1测试都验证了系统分数阶阶数在0.92~1.00时是混沌的.本文还详细介绍了CHAOS_PART和MUL_ACC_PART两个模块，并用FPGA实现了该系统.在示波器上获得了相应的混沌吸引子，验证了基于GL定义的分数阶简化Lorenz系统的硬件可实现性.

参考文献 (14)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回