高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

一种基于循环生成式对抗网络的去雾算法

, 

上一篇

下一篇

李潇雯, 袁太生. 一种基于循环生成式对抗网络的去雾算法[J]. 西南师范大学学报(自然科学版), 2020, 45(9): 132-138. doi: 10.13718/j.cnki.xsxb.2020.09.020
引用本文: 李潇雯, 袁太生. 一种基于循环生成式对抗网络的去雾算法[J]. 西南师范大学学报(自然科学版), 2020, 45(9): 132-138. doi: 10.13718/j.cnki.xsxb.2020.09.020
shu
Xiao-wen LI, Tai-sheng YUAN. A De-hazing Algorithm Based on Cycle Generative Adversarial Network[J]. Journal of Southwest China Normal University(Natural Science Edition), 2020, 45(9): 132-138. doi: 10.13718/j.cnki.xsxb.2020.09.020
Citation: Xiao-wen LI, Tai-sheng YUAN. A De-hazing Algorithm Based on Cycle Generative Adversarial Network[J]. Journal of Southwest China Normal University(Natural Science Edition), 2020, 45(9): 132-138. doi: 10.13718/j.cnki.xsxb.2020.09.020
shu

一种基于循环生成式对抗网络的去雾算法

  • 1.

    山西工商学院 计算机信息工程学院，太原 030006

  • 2.

    太原学院 计算机工程系，太原 030006

  • 基金项目: 山西省教育厅教育科学“十三五”规划项目(GH-16166)；山西省1331工程立德树人好老师课程建设计划支持人选项目(201832)
详细信息
    作者简介:

    李潇雯(1981-)，女，硕士，讲师，主要从事数据挖掘及大数据研究 .

  • 中图分类号: TP391.4

A De-hazing Algorithm Based on Cycle Generative Adversarial Network

  • 1.

    College of Computer and Information Engineering, Shanxi Technology and Business College, Taiyuan 030006, China

  • 2.

    Department of Computer Engineering, Taiyuan University, Taiyuan 030006, China

  • 摘要: 针对现有基于学习的去雾算法在处理过程中需要成对的数据来训练网络参数的问题，提出了一种基于循环生成式对抗网络的去雾算法.该算法通过使用编码器-解码器(Encoder-Decoder，ED)体系结构来构建生成器网络，然后采用一种不成对的图像训练方法来训练网络参数，估计出传输图，最后根据估计的传输图和大气光值，利用光学模型恢复出无雾清晰图像.实验结果表明：对于室内、外有雾图像，本文提出的方法可以在不发生任何颜色失真的情况下恢复无雾场景，而且相对于其他方法，该方法在多个评价指标上都有明显的性能优势.
    Abstract: Aiming at the problem that existing learning-based de-hazing algorithms need paired data to train network parameters in the process of dehazing, a new algorithm based on Cycle Generative Adversarial Network has been proposed. The algorithm constructs a generator network with an Encoder-Decoder (ED) architecture, and then uses an unpaired image training method to train network parameters and estimate the transmission map. Finally, based on the estimated transmission map and atmospheric light values, an optical model is used to recover a haze-free clear image. The experimental results show that the proposed method can restore the fog free scene without any color distortion for indoor and outdoor fog images, and has obvious performance advantages over other methods in multiple evaluation indexes.
  • 加载中

  • 图 1  生成式对抗网络的流程示意图

    下载: 全尺寸图片 幻灯片

    图 2  循环生成式对抗网络示意图

    下载: 全尺寸图片 幻灯片

    图 3  生成器网络架构示意图

    下载: 全尺寸图片 幻灯片

    图 4  循环不成对训练流程示意图

    下载: 全尺寸图片 幻灯片

    图 5  D-Hazy数据集中白板模糊图像的复原结果

    下载: 全尺寸图片 幻灯片

    图 6  D-Hazy数据集中走廊模糊图像的复原结果

    下载: 全尺寸图片 幻灯片

    图 7  真实的模糊图像(一)的复原结果

    下载: 全尺寸图片 幻灯片

    图 8  真实的模糊图像(二)的复原结果

    下载: 全尺寸图片 幻灯片

    图 9  真实的模糊图像(三)的复原结果

    下载: 全尺寸图片 幻灯片

    表 1  不同数据集的信息

    数据集 训练 测试
    D-HAZY 200 1 249
    室外自然 900 100
    室外合成 0 1 000
    SOTS 0 500
    下载: 导出CSV

    表 2  不同算法在3个数据集上的测试结果

    算法 测试项 PSNR SSIM GMSD
    本文方法 D-HAZY 13.95 0.751 0.069
    DDN 10.92 0.738 0.091
    Cycle-GAN 13.59 0.649 0.102
    Cycle-Dehaze 12.57 0.675 0.098
    本文方法 SOTS 21.37 0.889 0.079
    DDN 19.35 0.824 0.101
    Cycle-GAN 14.18 0.575 0.117
    Cycle-Dehaze 15.86 0.697 0.098
    本文方法 室外合成 22.93 0.894 0.082
    DDN 21.19 0.853 0.099
    Cycle-GAN 12.05 0.383 0.125
    Cycle-Dehaze 12.54 0.461 0.122
    下载: 导出CSV
  • [1] 谢伟, 余瑾, 涂志刚, 等.消除光晕效应和保持细节信息的图像快速去雾算法[J].计算机应用研究, 2019, 36(4): 1228-1231. doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjyyyj201904060
    [2] 何立风, 钟岩, 刘艳玲, 等.一种改进的基于暗通道先验去雾算法[J].计算机应用与软件, 2019, 36(2): 57-61. doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjyyyrj201902012
    [3] 张宝山.结合直方图均衡化和暗通道先验的单幅图像去雾算法研究[D].兰州: 兰州交通大学, 2018.http://cdmd.cnki.com.cn/Article/CDMD-10732-1018234548.htm
    [4] 张驰, 谭南林, 李响, 等.基于改进型Retinex算法的雾天图像增强技术[J].北京航空航天大学学报(自然科学版), 2019, 45(2): 309-316. doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bjhkhtdxxb201902011
    [5] LI B, PENG X, WANG Z, et al. AOD-Net: All-in-One Dehazing Network [C]// 2017 IEEE International Conference on Computer Vision (ICCV). Beijing: IEEE, 2017.https://www.researchgate.net/publication/322060481_AOD-Net_All-in-One_Dehazing_Network
    [6] LI R, PAN J, LI Z, et al. Single Image Dehazing via Conditional Generative Adversarial Network [C]// 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Salt Lake City: IEEE, 2018.https://www.researchgate.net/publication/329740444_Single_Image_Dehazing_via_Conditional_Generative_Adversarial_Network
    [7] ZHANG H, PATEL V M. Densely Connected Pyramid Dehazing Network [C]// 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Salt Lake City: IEEE, 2018.https://www.researchgate.net/publication/323956849_Densely_Connected_Pyramid_Dehazing_Network
    [8] REN W, MA L, ZHANG J, et al. Gated Fusion Network for Single Image Dehazing [C]// 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Salt Lake City: IEEE, 2018.
    [9] LIANG T Y, STOKES J. Interaction Matters: a Note on Non-asymptotic Local Convergence of Generative Adversarial Networks [C]//2019 22nd Artificial Intelligence and Statistics (AISTATS). Naha: IEEE, 2019.https://www.researchgate.net/publication/323276304_Interaction_Matters_A_Note_on_Non-asymptotic_Local_Convergence_of_Generative_Adversarial_Networks
    [10] ZHU J Y, PARK T, ISOLA P, et al. Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks [C]//2017 IEEE Conference on Computer Vision and Pattem Recognition (CVPR). Honolulu: IEEE, 2017.https://www.researchgate.net/publication/322060135_Unpaired_Image-to-Image_Translation_Using_Cycle-Consistent_Adversarial_Networks
    [11] ANCUTI C, ANCUTI C O, DE VLEESCHOUWER C. D-HAZY: A Dataset to Evaluate Quantitatively Dehazing Algorithms [C]//2016 IEEE International Conference on Image Processing (ICIP). Phoenix: IEEE, 2016.https://www.researchgate.net/publication/307516141_D-HAZY_A_dataset_to_evaluate_quantitatively_dehazing_algorithms
    [12] YUAN F, HUANG H. Image Haze Removal via Reference Retrieval and Scene Prior [J]. IEEE Transactions on Image Processing, 2018, 27(9): 4395-4409. doi: 10.1109/TIP.2018.2837900
    [13] 张珂, 高策, 郭丽茹, 等.非受限条件下多级残差网络人脸图像年龄估计[J].计算机辅助设计与图形学学报, 2018, 30(2): 346-353. doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjfzsjytxxxb201802016
    [14] YANG X, XU Z, LUO J. Towards Perceptual Image Dehazing By Physics-Based Disentanglement and Adversarial Training [C]//Thirty-second AAAI conference on artificial intelligence. New Orleans: AAAI, 2018.
    [15] ENGIN D, GENÇ A, KEMAL EKENEL H. Cycle-Dehaze: Enhanced Cyclegan for Single Image Dehazing [C]//2018 IEEE Conference on Computer Vision and Pattern Recognition Workshops(CVPRW). Salt Lake City: IEEE, 2018.
  • 加载中
图( 9) 表( 2)
计量
  • 文章访问数:  807
  • HTML全文浏览数:  807
  • PDF下载数:  142
  • 施引文献:  0
出版历程
  • 收稿日期:  2019-08-15
  • 刊出日期:  2020-09-20

一种基于循环生成式对抗网络的去雾算法

    作者简介: 李潇雯(1981-)，女，硕士，讲师，主要从事数据挖掘及大数据研究
  • 1. 山西工商学院 计算机信息工程学院，太原 030006
  • 2. 太原学院 计算机工程系，太原 030006
  • 收稿日期:  2019-08-15
基金项目:  山西省教育厅教育科学“十三五”规划项目(GH-16166)；山西省1331工程立德树人好老师课程建设计划支持人选项目(201832)

摘要: 针对现有基于学习的去雾算法在处理过程中需要成对的数据来训练网络参数的问题，提出了一种基于循环生成式对抗网络的去雾算法.该算法通过使用编码器-解码器(Encoder-Decoder，ED)体系结构来构建生成器网络，然后采用一种不成对的图像训练方法来训练网络参数，估计出传输图，最后根据估计的传输图和大气光值，利用光学模型恢复出无雾清晰图像.实验结果表明：对于室内、外有雾图像，本文提出的方法可以在不发生任何颜色失真的情况下恢复无雾场景，而且相对于其他方法，该方法在多个评价指标上都有明显的性能优势.

English Abstract

    全文HTML

  • 雾霾由气溶胶组成，这些气溶胶粒子会对场景对象反射的光产生散射，导致能见度下降.在拍摄图像时，气溶胶的存在会减弱场景点的强度，降低图像质量.因此，在模糊环境下，单图像模糊去除是提高计算机视觉算法性能的一项具有挑战性的预处理任务[1].

    目前，图像除雾算法大致可以分为基于模型、基于非模型和基于学习的3类方法.基于模型的图像去雾算法是利用退化的物理模型来尽可能恢复清晰图像的技术，经典的复原方法有暗通道先验方法(Dark Channel Prior，DCP)[2]，这类方法畸变较小，去雾效果很好，但是由于计算复杂度较高，实时处理比较困难.基于非模型的算法是根据人类视觉感受，通过增强图像对比度来达到去雾的目的，常规图像增强算法如直方图均衡化[3]和基于Retinex理论的图像增强[4]，这类方法通过提高图像对比度降低雾霾对图像的影响，但是也容易造成过增强或者信息损失现象.随着深度学习的快速发展，基于深度学习的图像去雾算法已经取得良好的效果. Li等[5]提出一种运用端到端卷积神经网络(Convolutional Neural Network，CNN)进行图像去雾的算法，该方法通过设计新的大气散射模型，在不需要计算传输矩阵和大气光的情况下，直接利用轻量CNN生产清晰图像.文献[6]提出一种基于条件生成式对抗网络的恢复图像算法，通过引入VGG特征和L1正则化梯度先验，直接将模糊图像恢复至清晰图像. Zhang等[7]提出一种密连通金字塔去雾算法，通过将大气散射模型嵌入到网络中，实现传输图和大气光的端到端联合学习，提升去雾效果. Ren等[8]提出利用编码器和解码器组成的端到端可训练神经网络进行去雾的算法，通过引入多尺度的方法，避免光环伪影的出现，实现从模糊输入中直接恢复清晰图像的目的.

    虽然上述方法可以实现直接对模糊图像去雾的目的，但是这些网络需要成对的数据，即合成的模糊输入图像和相应的真实图像来训练网络参数，用以估计传输图.由于合成的模糊图像不包含实际世界中的真实模糊分布和场景中的雾度分布，因此采用配对训练网络的去雾算法缺少一定的信服度.针对这个问题，本文提出一种基于循环生成式对抗网络的去雾算法，通过采用编码器-解码器(Encoder-Decoder，ED)体系结构来构建生成器网络，然后使用一种不成对的图像训练方法来训练网络参数，估计传输图，最后通过光学模型恢复无雾清晰图像.

1.   生成式对抗网络

  • 生成式对抗网络(Generative Adversarial Network，GAN)是根据博弈论中的零和博弈思想提出的一种神经网络模型[9]. GAN模型具有强大的图片生成能力，在图像恢复和合成方面有着广泛的应用.

    • 1.1.   标准GAN

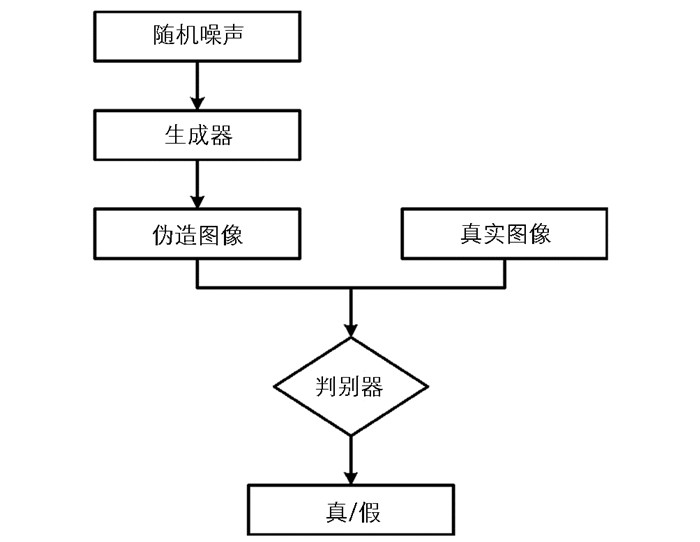
  • 标准GAN是一种通过对抗过程估计生成模型的网络框架，该网络的基本框架由一个生成网络G和一个判别网络D构成，GAN的流程如图 1所示.

    生成网络G利用真实数据样本Ix训练生成新的数据样本G(Ix)，判别网络D是一个二分类器，判断样本是来自于原始数据Ix，还是由生成网络产生G(Ix).整个GAN过程网络G与D同时运行，判别网络的目的是尽量使D(G(Ix))接近0，而生成网络的目的是尽量使它接近1，最终二者在博弈中达到平衡.

    为了约束网络，GAN的损失函数被定义为

    其中，P表示概率分布， E表示期望.

    GAN模型的目标函数表示为

    • 1.2.   循环生成式对抗网络

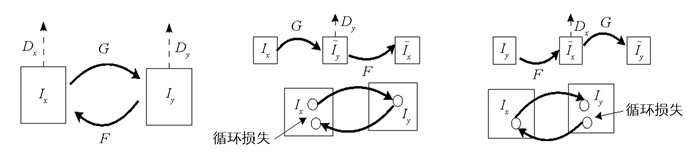
  • 循环生成式对抗网络(Cycle Generative Adversarial Networks，CGAN)[10]是在条件生成式对抗网络的基础上，利用循环损失函数和对抗损失函数加权求和的方式，约束网络学习得到有雾Ix和清晰Iy两种类型图像之间的映射关系，而且不需要两类图像一一匹配，具体流程如图 2所示.

    其中，G和F分别表示Ix→Iy和Iy→Ix的映射函数，Dy和Dx是与之相对应的判别网络. Dy的目标是保证输入Ix通过映射函数G的转换得到的输出G(Ix)与Iy无差别，Dx则保证输入Iy通过映射函数F的转换得到的输出F(Iy)与Ix无差别.

    损失函数可以表示为

    为了进一步规范映射，除了通过两个损失函数约束外，还引入循环损失函数

    因此，循环生成式对抗网络的目标函数为

    其中，λ是控制参数.

2.   基于循环生成式对抗网络去雾算法

  • 本文利用非配对训练方法对有雾图像的传输图进行估计，然后利用光学模型对有雾图像进行恢复.

    • 2.1.   光学模型

  • 在图像处理中最常用的单色大气散射模型如式(7)所示.

    其中，χ=(x，y)表示图像坐标，I(χ)为雾天摄像机收到的光强，R(χ)表示实际场景中辐射强度，T(χ)为传输图，A为大气光.

    由式(7)分析可知，去雾后的复原图像R(χ)求解可以通过式(8)转化为对传输图T(χ)和大气光A的估算.

    根据式(7)，传输图T(χ)可以表示为

    其中，本文利用暗通道先验的方法[2]估算全球大气光A.

    • 2.2.   去雾网络

  • 本文提出了基于循环生成式对抗网络的去雾网络，其中生成器网络是一种包含跳跃连接的编码器-解码器架构.编码器网络的作用是通过保持目标的结构信息，从输入图像中获取抽象特征映射；解码器网络的目的是从编码器网络获得的低分辨率目标显著性图中再现高分辨率特征图.本文提出的去雾算法利用ED架构的这些特性来获得精确的传输图.

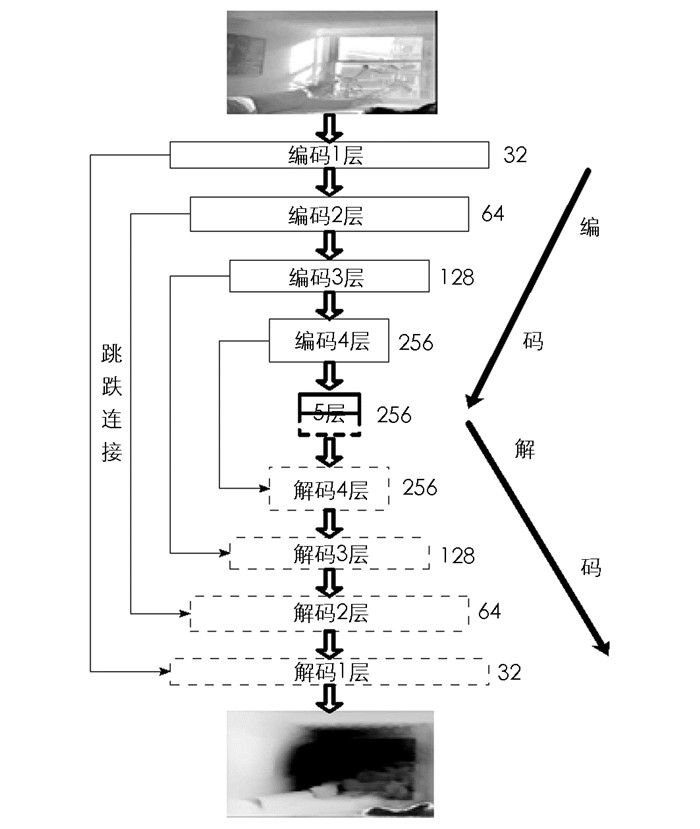
    为了获取目标层传输图，本文设计一种面向对象级传输信道信息的生成器网络ED体系结构，具体结构如图 3所示.

    生成器网络由5个编码器层和5个解码层块组成.每个编码器层由卷积层、实列正则化、泄漏ReLU组成.每个解码器层由反褶积层、drop-out层、实列正则化、连接层(跳跃连接)、泄漏ReLU组成. ED架构中的空间滤波器大小是恒定的，整个网络为3×3.在每个编码器块上，卷积层步长为2.另一方面，解码器体系结构中也是类似设置，如3×3反卷积滤波器，上采样系数为2.为了避免过拟合，drop-out层的辍学率为0.5，泄漏ReLU的泄漏系数为0.2.此外，使用实列正则化来规范化卷积层的特征映射.对于判别器网络，由于Cycle-GAN架构的判别器在图像到图像的风格转换任务中取得良好的效果，因此本文也采用相同的网络.

3.   实验结果与分析

  • 本文所有实验在一台配置为Intel Xeon E5-2698 (20-Core) CPU @2.20 GHz和NVIDIA Tesla V100 4×16 GB GPU的NVIDIA DGX工作站上进行.

    • 3.1.   数据集及训练设置

  • 本文采用D-Hazy[11]和SOTS[12]两个公开可用的室内合成模糊图像数据库，用来评估所提出的去雾算法. D-Hazy是一个用于图像去雾的标准数据集，它由1 449张合成密集的模糊图像及其各自的无雾图像组成.本文使用200张图像用于网络参数的训练，剩余1 249张图像对所提出的单图像去雾方法进行测试.室内SOTS数据库由500幅合成模糊图像及其各自的无雾图像组成.此外，从ImageNet数据库(海滩、公路和天空等)[13]中随机选择1 000个室外图像，将其分为室外有雾和无雾图像两组. A组由有雾图像组成，B组由无雾图像组成，图像集A和图像集B之间没有一一对应关系.然后，通过合成将雾添加到这些图像中，这些从ImageNet数据库中合成的有雾图像称为室外合成数据集. 表 1给出了不同数据集进行网络训练和测试的图像数量.

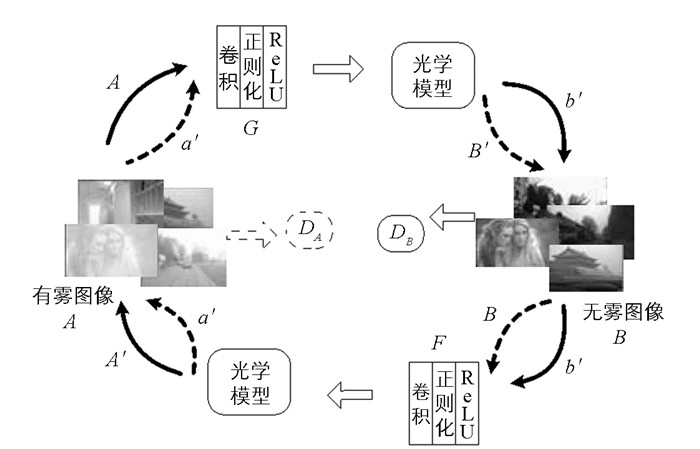
    在网络训练时，对D-Hazy数据集中室内模糊图像及其相应的无模糊图像进行洗牌，以实现未配对的监督训练.将ImageNet数据库选择的室外有雾和无雾图像分为两组，A组为有雾图像集，B组为无雾图像集，图像集A和B之间没有一一对应关系. 图 4显示了用于训练的去雾网络不成对训练方法.如图 4所示，该去雾网络包括两个映射：从模糊映射到清晰的正向映射和从清晰映射到模糊的反向映射.

    • 3.2.   实验结果与分析

  • 为了更好地评价去雾算法的性能，本文从定性和定量两个方面进行评估.

    • 3.2.1.   定性分析

  • 图 5-图 6给出了不同去雾算法在D-Hazy数据集合成室内模糊图像的复原结果.从图 5-图 6中可以看出，本文算法在不发生任何颜色失真的情况下恢复无雾场景.对比其他算法，从图 5中发现，使用DDN[14]，Cycle-GAN[10]和Cycle-Dehaze[15]方法恢复的图像存在颜色失真的现象. 图 6显示Cycle-GAN和Cycle-Dehaze两种端对端的算法无法恢复标记区域中的文本，但基于光学模型的DDN算法和本文算法可以将文本恢复，而且本文算法清晰度更高，这充分体现出本文ED架构的优势.

    对于真实的模糊图像，图 7-图 9给出了不同方法的复原结果.从图 7-图 9中可以看出，使用DDN，Cycle-GAN和Cycle-Dehaze方法恢复的图像存在颜色扭曲的现象，无法恢复至视觉上令人愉悦的无雾场景.本文算法通过学习雾扩散和恢复无雾场景来克服颜色失真问题，虽然在图 9中不能完全消除雾霾，复原的图像清晰度不太高，但与其他方法相比仍具有一定的优势.

    • 3.2.2.   定量分析

  • 为了进一步验证，本文利用峰值信噪比(PSNR)、结构相似性指数(SSIM)和梯度幅度相似度偏差(Gradient Magnitude Similarity Deviation，GMSD) 3个评价指标来验证算法的有效性.

    PSNR表示滤波图像的最大像素值与噪声的比值，定义为

    其中，MSE表示均方误差，fmax和fmin分别表示去噪图像的最大和最小像素. PSNR越大，说明去噪图像失真越小，图像的去噪效果越好.

    基于感知模型的归一化度量SSIM定义为

    其中，$ l\left( {x, {\rm{ }}y} \right) = \frac{{2{u_x}{u_y} + {c_1}}}{{u_x^2 + u_y^2 + {c_1}}}, $$c\left( {x, {\rm{ }}y} \right) = \frac{{2{\sigma _x}{\sigma _y} + {c_2}}}{{\sigma _x^2 + \sigma _y^2 + {c_2}}}, $$ s\left( {x, {\rm{ }}y} \right) = \frac{{{\sigma _{xy}} + {c_3}}}{{{\sigma _x}{\sigma _y} + {c_3}}}$分别表示亮度比较、对比度比较和结构比较，x，y分别为参考图像和待测图像，ux，uy，σx2，σy2，σxy分别表示图像x，y的均值、方差和协方差，c1，c2，c3为很小的常数. SSIM从亮度(均值)、对比度(方差)和结构3个层次比较图像失真，但经常用于比较去噪图像与原始图像间的结构相似性，SSIM在[-1, 1]区间范围内取值，其值越接近1，说明两者结构相似性越好；相反，相似性越差.

    图像梯度对图像失真程度高度敏感，局部质量下降与全局图像的偏差GMSD可以反映图像的质量，通常运用图像与线性滤波器Prewitt算子的卷积来提取图像梯度.

    其中，mIGT，mIHR分别表示图像IGT和IHR的梯度幅度，hx，hy分别表示Prewitt滤波器的水平和竖直方向算子.计算梯度幅度相似度均值为

    其中，N表示图像总像素量，$ GMS\left( i \right) = \frac{{2{m_{{I^{GT}}}}\left( i \right) \cdot {m_{{I^{HR}}}}\left( i \right) + c}}{{m_{{I^{GT}}}^2\left( i \right) + m_{{I^{HR}}}^2\left( i \right) + c}}$表示像素i处的梯度幅度相似度.

    因此，梯度幅度相似度偏差可以被定义为

    GMSD的值反映整幅图像的失真严重程度，其值越高，图像失真程度越高，质量越差.

    表 2给出了不同算法在3个数据集上测试的平均PSNR，SSIM和GMSD指标结果.从表 2中可以清楚地看到，相较于其他算法，本文方法的去雾性能有明显的提升.

4.   结语

  • 针对图像配对训练网络的去雾算法缺少一定信服度这个问题，本文提出一种基于循环生成式对抗网络的去雾算法.该算法基于编码-解码器的架构来构建对抗网络中的生成器，然后采取不成对的图像训练方式对网络参数进行训练，用于估计传输图，最后通过光学模型恢复无雾清晰图像.实验结果表明，对于室内、外合成图像，本文方法恢复的无雾图像不存在任何颜色失真现象，而且本文算法在性能上明显优于其他方法.

参考文献 (15)

目录

版权所有：西南师范大学学报(自然科学版)

地址：重庆市北碚区西南大学 电话：023-68252540，68254576，68254478 电子邮箱：xbbjb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回