-
搅拌生物反应器由于其出色的传热、传质性能而被广泛应用于生物发酵、制药和化工生产等相关领域. 对于微生物发酵而言,影响发酵产量的因素众多:培养基配比、pH值、温度、搅拌转速、通气速率以及发酵液自身流体特性等[1-2]. 阴沟肠杆菌发酵生产盐藻多糖的过程属于有氧发酵,在发酵过程中,发酵液的黏度由于微生物的生长而逐渐增加,发酵液显示出剪切稀化的假塑性流体性质. 已有的关于假塑性流体充气混合的研究集中于预先选择的发酵黏度,但缺乏对于发酵过程的整体对比评估[3-4]. 事实上,阴沟肠杆菌发酵经历了从发酵前期、中期到后期的黏度变化阶段,因此为了在工业规模的搅拌罐中实现高效生产,有必要去探究不同阶段的发酵液对于搅拌罐内流体动力特性的影响.
随着计算机技术的发展,在搅拌与混合领域越来越多的研究者选择使用基于计算流体力学(CFD)的数值模拟方法来探究搅拌罐中发酵液的流动特性. CFD可以提供强大的能力来计算模拟发酵液的流动[5]及气体和液体的相互作用[6],并且可以获得气体滞留和功率消耗的最终信息[7-8]. 目前的研究针对小型发酵设备进行仿真居多,并已经得到了许多有价值的成果. 随着CFD技术的发展和成熟,越来越多的研究者开始转向更大规模发酵罐的流场数值模拟[9-11],但实现从实验室规模到生产规模的模拟仍然面临艰巨挑战.
本研究选择发酵生产中常见的50L中型发酵设备,以希望获取到更为接近于实际发酵应用的流场信息,进而指导发酵设备设计和工业生产. 选择生产岩藻多糖的阴沟肠杆菌发酵过程中第12,36,60 h的发酵液为研究目标,使用旋转流变仪测量发酵液流动特性,并对搅拌罐进行建模,使用结合了群体平衡模型(PBM)的Euler-Euler方法对三层充气搅拌罐中的发酵液进行了数值模拟,得到了搅拌罐中液体流动特性和气泡分散状态,并对三阶段的发酵液气体滞留和功率消耗进行对比分析.
全文HTML
-
随着发酵的进行,发酵液中微生物与产物浓度的升高使得发酵液的流变性质发生了改变,从而使大多数发酵液具有非牛顿流体的属性. 本次研究的发酵液为生产岩藻多糖的阴沟肠杆菌发酵液,属于假塑性流体,具有剪切变稀特性,可以使用幂律方程描述该发酵液[12]:
式中,μα为表观黏度;γα为表观剪切速率;K为流体稠度系数;n为流动行为指数. 使用DHR-1旋转流变仪(Ta设备,USA). 测量选取3~5 mL样品,剪切速率设置为0.1~100/s,并选择直径为40 mm的标准平板进行测量. 在预设的剪切速率下测量15个黏度数据. 环境温度设置为25 ℃,与实验时搅拌槽内温度相同. 通过幂律模型拟合获得了发酵液第12,36,60 h的K和n流变参数.
-
本次建模选择50 L生物发酵罐,并对其结构进行适当简化. 微生物发酵使用三层组合搅拌桨:上层搅拌桨为四叶旋桨式搅拌桨,中层和下层搅拌桨为Rushton搅拌桨,具体的结构尺寸见表 1,总体几何模型如图 1(a)所示.
在ANSYS ICEM CFD 16.0中进行网格划分,采用混合网格划分策略,基于发酵罐结构以及搅拌流场模拟方法考虑,将模拟区域分为搅拌桨内区域、搅拌桨外区域和发酵罐底部区域3个部分. 由于发酵罐底部结构和搅拌桨不规则,发酵罐底部区域和搅拌桨内区域采用非结构化网格,搅拌桨外区域采用结构化网格,并最终合并结构化网格和非结构化网格生成混合网格,网格总数935028. 发酵罐网格如图 1(b)所示.
-
在Solidworks 2016中创建搅拌罐的3D模型,ICEM18.1用于划分搅拌罐的非结构化网格,最后将网格导入到Fluent 18.1中转化为多面体网格求解. 气液两相流的求解采用Euler-Euler双流体模型[13-14].
连续性方程表示为
式中,
$ {\overrightarrow v _i}$ 为i相的速度矢量,m/s;ρi为i相的密度,kg/m3;αi为i相的体积分数,%.动量方程表示为
式中,
$ {\overline{\overline \tau } _i}$ 为应力应变张量;$ \vec{F}_{i}$ 为外部体积力,N;$ \vec{F}_{\mathrm{lift}, i}$ 为升力,N;$ \vec{F}_{w l, i}$ 为壁面润滑力,N;$\vec{F}_{v m, i}$ 为虚拟质量力,N;$\vec{F}_{t d, i} $ 为湍流扩散力,N;$ \vec{R}_{i}$ 为相间作用力,N;p为两相之间的压力,N.在搅拌罐中升力、虚拟质量力和壁面润滑力相对于曳力来说很小[15],对于最终发酵液的影响不明显,因此本次仿真忽略掉这些力的影响.
曳力模型选用默认的Schiller-Naumann模型[16]:
式中,
$ C_{D}=\left\{\begin{array}{ll} 24\left(1+0.15 R e^{0.687}\right) / R e & R e \leqslant 1000 \\ 0.44 & R e \geqslant 1000 \end{array}\right.$ ;Re为雷诺数.湍流扩散力选用Lopez de Bertodano模型:
式中,ki为连续相的湍动能,m2s3;
$ \nabla \alpha_{j}$ 为离散相的梯度;CTD是一个可变的常数,本文CTD=1. -
在搅拌模拟领域中,常见的模型有标准k-e模型、RNG k-e模型、Relizablek-e模型以及SST k-ω模型,这些模型都被研究者广泛使用. 本次仿真所针对的发酵液黏度较高,SST k-ω模型能够适应于较高黏度的搅拌模拟,并且这种模型被证明对发酵液搅拌模拟具有良好的效果[17],因此选择使用此模型:
其中,Gk表示平均速度梯度产生的湍流动能生成项;Gω表示比耗散率生成项;Γk和Γω分别表示湍动能和比耗散率的有效扩散系数;Yk和Yω分别表示由湍流引起的湍动能和比耗散率的耗散项;Dω表示交叉扩散项.
-
在搅拌罐中因通气和搅拌桨的存在,使气泡上升过程中会发生聚并和破碎,最终搅拌罐中存在大量气泡,并以一定尺寸分布. 群体平衡方程是描述多相流体系中颗粒状态分布随时间与空间连续变化的偏微分方程. 假定φ为粒子体积,数量密度函数的传递方程为
式中,
$ \overrightarrow u $ 表示粒子的传输速度;Gv表示体积增长速率,m3/s;a(V-V′,V′) 表示体积为V-V′和体积V′的粒子的聚并频率,1/s; g(V)表示粒子的破碎频率,1/s;β(V|V′)表示粒子分布函数,无单位.其边界条件和初始条件为
其中,
$\dot{n}_{0} $ 是成核速率,单位为m3/s.在气泡的聚并过程中,聚并导致的粒子产生项表示为
体积为V的粒子的聚并死亡项表示为
破碎导致的粒子生成表示为
破碎导致体积为V的粒子的死亡表示为
本次仿真聚并与破碎模拟均选用Luo模型,该模型基于各向同性湍流和概率理论,用于解决湍流悬浮液中的液滴和气泡破裂问题[18]. 另外,考虑到气泡的大小及分散状况,气泡一共分为10组,气泡尺寸范围从1~27.8 mm.
-
考虑到重力对发酵液流场的影响,搅拌发酵液表面压力值设置为标准大气压. 数值模拟的方式选择为滑移网格法,采用有限体积法离散微分方程,对压力速度耦合选用SIMPLC算法,对流项和扩散项的离散采用QUICK格式. 气体分布器气体入口边界条件设定为速度入口,搅拌罐顶部出口边界条件为压力出口,所有壁面设定为无滑移的壁面边界条件. 计算采用瞬态计算的方法,时间步长设置为0.005,当计算残差达到10-3时仿真收敛. 数值计算中,搅拌罐设置与实际发酵环境相同:搅拌转速为500 r/min,通气比为1.2 vvm.
-
基于CFD模拟的功率(P)和混合指数(MI)用于评估发酵罐在不同发酵阶段的搅拌性能.
搅拌罐功率表示为
式中,P为功率消耗,W; M为扭矩,Nm;N为搅拌桨转速,r/min.
混合指数表示为
式中,MI为混合指数;σ为i点的局部气含率,%;
$ \overline \sigma $ 为取样点的平均气含率,%;取样点在竖直平面YZ平面上,水平y=D/4即y=75 mm处,D为搅拌罐直径,高度z在0~500 mm范围内均匀取15个点.
1.1. 流变测量
1.2. 发酵罐建模与网格划分
1.3. CFD数值模拟
1.3.1. 控制方程
1.3.2. SSTk-ω湍流模型
1.3.3. 群体平衡模型
1.3.4. Fluent模块设置
1.3.5. 仿真后处理
-
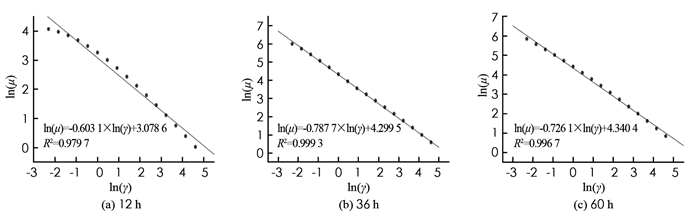
对式(1)左右两边同时取对数可得:
进一步对实验数据点按式(16)进行拟合可得流变对数曲线图,如图 2所示. 第12,36,60 h发酵液拟合回归方程决定系数R2分别为0.979 7,0.999 3,0.996 7,阴沟肠杆菌发酵液流变曲线较好地满足幂律分布,幂律方程参数K和n如表 2所示.
由幂律模型参数表可知,在发酵液初期发酵液黏度上升较快,发酵液后期黏度增长缓慢,原因可能为发酵前期微生物增长速度较快,此时的发酵液黏度上升较快,后期由于菌体衰老自溶,此时发酵液的黏度上升较为缓慢. 在Fluent中定义新的工作介质,选择Power-law(幂律函数)并将K和n输入,用于接下来的数值模拟对比.
-
仿真收敛后通过CFD-post处理仿真数据得到发酵罐速度场分布,如图 3所示. 图 3(a)为速度矢量图,图 3(b)为速度云图. 由速度矢量图可得:中层和下层搅拌桨为径向流搅拌桨,在搅拌区域内形成上下两个循环区域,液体经过直桨叶片向直径方向排出,到达发酵罐外壁面时,分成了上下两股液分别向上向下流动,最后两股液体经由流动汇集到搅拌轴附近;上层搅拌桨为轴向流下压式搅拌桨,发酵液经过它的搅拌向下方流动,此搅拌桨主要是为了将上升的气体下压,延长气体在液体中的停留时间,以此提高气含率,保证生物发酵反应的持续进行. 由速度云图可得:发酵液黏度越高,发酵罐“洞穴”现象越显著. 搅拌桨对靠近壁面处的发酵液混合效应减弱,在发酵罐内出现混沌隔离区.
-
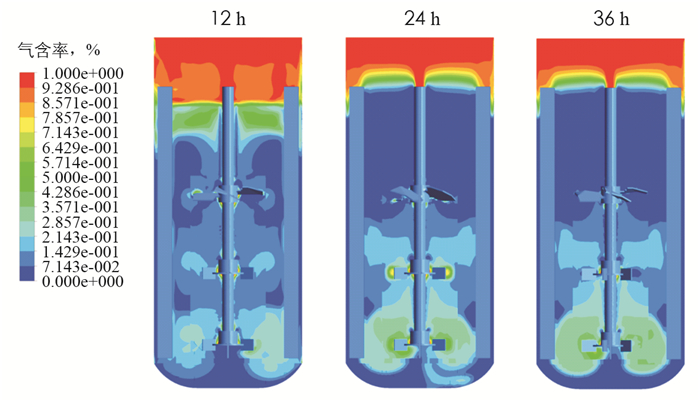
图 4为气体在发酵体系中的体积分数,称为气含率云图. 由气含率云图可知,空气通过进气管从发酵罐底部进入,并随着整个搅拌流场流动,最终从顶部逃逸出发酵体系. 从气含率云图中还可以看出,在下层搅拌桨附近存在较高的气含率,中层桨次之,而上层搅拌桨最少,这主要是由于气体从底部通入,率先在底部搅拌桨的带动下进行分散和循环,而随着时间的推移,气体受到各项力的作用而向上运动,使得中层桨和上层桨附近也聚集到更多的气体. 在自由液面处,气含率显示出较高的水平,这也是气体逃逸所产生的结果. 由发酵罐内自由液面高度的上升可知,发酵罐内的气含率不断上升,这主要由于发酵罐内黏度的上升导致气体逃逸困难导致. 分界面之外的气含率也展现出与实际情况相符合的结论,即液体的飞溅与粘附.
-
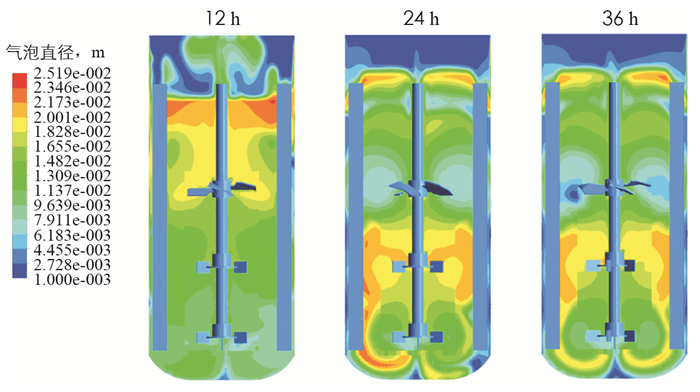
通过后处理得出气泡直径在发酵罐中的分布情况,如图 5所示. 从图中可以看出整个发酵罐内气泡尺寸范围处于1~25.19 mm之间. 对于发酵前期(12 h)而言,发酵液黏度较小,气体上升容易,在靠近底层的搅拌桨附近气泡尺寸相对偏小,而随着高度的增大,气泡尺寸也逐渐增大,在离自由液面处的气泡尺寸显示出发酵液范围内的最大值. 对于发酵中后期(36 h和60 h)而言,由于发酵液的高黏度的阻碍作用与上层四叶旋桨的下压作用,气体在下部聚集、合并导致中下部分的气泡直径增大. 随着气体的上升,在自由液面处气体所受液相压力变小,气泡尺寸逐渐变大.
-
功率消耗(P)和混合指数(MI)用于定量评价搅拌前期、中期和后期的混合性能. 结果如表 3所示:
由表 3可知,随着发酵过程的进行,搅拌罐的功率消耗不断上升,功率消耗与黏度变化呈正相关. 同时在相同的转速与通气速率下,发酵中后期的混合指数变高,这意味着发酵罐内的混合效果变差,发酵进程可能受阻. 因此,在阴沟肠杆菌发酵生产岩藻多糖发酵中期和后期阶段中应该提高搅拌转速与通气速率使发酵罐获得更小的混合指数,即更好的气体混合分散效果,以提高发酵效率.
2.1. 发酵液流变参数
2.2. 液体速度云图
2.3. 气含率分布
2.4. 气泡尺寸分布
2.5. 功率与混合指数
-
文章研究了阴沟肠杆菌72 h发酵过程中发酵液的流变特性,基于CFD-PBM的耦合模型对50 L三层发酵罐中的发酵前期、中期和后期流场进行了数值模拟,得到的主要结论如下:
1) 发酵液在发酵前期(12 h)、发酵中期(36 h)和发酵后期(60 h)的发酵液黏度不断上升,流变曲线呈现较好的幂律分布,回归方程决定系数R2分别为0.979 7,0.999 3和0.996 7.
2) 速度矢量图和速度云图直观地表现了搅拌罐中的流场和流结构. 搅拌过程中在50 L搅拌罐中形成了3个循环流动,同时随着发酵液黏度的上升,发酵液出现混沌隔离区,搅拌桨的混合效应减弱.
3) 随着发酵过程的进行,搅拌罐内的气含率和功率也随之升高. 由气泡直径云图可知,发酵罐内的气泡尺寸范围为1~25.19 mm,黏度变化对气泡直径分布影响较大.
4) 由发酵过程的混合评价可知,阴沟肠杆菌发酵的中期和后期应该提高搅拌转速和通气速率来获得更佳的混合效果. CFD-PBM耦合模型作为一种有价值的数值模拟工具可以为微生物发酵的规模化生产提供数据参考和指导.




 下载:
下载: