-
在数据库管理领域,查询优化(query optimization,QO)是备受关注的热点问题.查询优化程序通过考虑可能的查询计划来调节最有效的方式用于评估给定的查询计划[1].近年来,来自不同资源的大量数据泛滥成灾,使得查询优化成为研究人员的一项艰巨任务.由于数据库结构复杂,特别是对于不太简单的查询,可以通过不同的方式、数据结构和顺序从数据库中收集查询所需的数据,不同的查询方式通常需要不同的处理时间[2-3].
在众包数据库系统中,用户需要提交基于结构化查询语言(SQL)的查询,然后系统负责查询编译,并生成执行计划和评估众包市场[4-5].在这个过程中,由于各种查询计划差异巨大,使得查询优化必不可少.为了减少查询处理时间和成本,研究人员开发了许多众包查询优化算法. Amini等[6]提出了一种基于众包的XML关键词搜索方法,利用了用户的参与来改进数据库和查询处理的流程. Cincy等[7]提出一种基于人工蜂群和蝙蝠算法(A-BAT)的众包系统查询优化方法,通过使用A-BAT算法计算用户最大访问量来找出优化产品,最大程度地降低成本和等待时间. Rekatsinas等[8]设计了一个自适应查询框架,通过构造目标域结构和使用排除列表来限制众包查询的重复提取. Bhaskar等[9]利用鲸鱼优化算法来优化基于位置的查询,并利用众包并行和串行处理来估计查询答案的准确性,降低计算时间和通信成本.
查询优化器通过估计货币成本和延迟时间来确定最佳查询计划.本文的创新之处在于将查询优化问题视为一个多目标优化问题,采用基于蚁狮优化的多目标优化方法,通过控制质量、最小化成本和时间的方式在众包查询中搜索最佳查询计划.蚁狮优化算法是一种元启发式算法,蚁狮优化器遵循蚂蚁随机游走、蚁狮建立陷阱、蚂蚁落入陷阱、蚁狮捕捉猎物和重建陷阱5个步骤,在控制质量的前提下,以延迟和查询成本作为目标函数,寻找满足要求的最佳查询计划.
全文HTML
-
众包技术作为一种新的计算范式,利用人类智能来解决计算机无法有效完成的问题,用于弥合基于机器计算和基于人类计算之间的鸿沟.在众包系统中,对于给定的请求者查询,系统首先将查询解析为具有人群驱动操作的查询计划,然后生成要在众包平台上发布的任务,最后收集人群的输入生成结果.
该系统包括用户查询、查询优化、众包执行和众包平台4个模块.首先,用户提交基于SQL的查询内容,然后智能查询优化器通过解析后找到合适的查询计划,并最终从查询成本和延迟的角度对其进行正确评估.查询优化器生成最佳查询计划后,在众包执行模块中执行,生成人类智能任务(human-intelligent tasks,HIT),并将这些HIT转移到众包平台上.基于从人群中收集的HIT答案,执行程序执行查询,并将生成的结果返回给用户.
众包系统中的优化机制大致可以分为基于规则和基于成本两类方法.基于规则的优化器仅应用一组规则,而不用估计成本来确定最佳查询计划.尽管基于规则的优化易于实现,但其优化能力有限,且容易出现执行计划无效的问题.基于成本的优化方法,可以通过估算备选查询计划的成本来评估查询结果,并选择估算成本最低的查询计划.当前查询优化方法大多采用基于成本的方式进行优化.
-
在关系数据库系统中,查询优化在提供声明性查询接口的众包系统中是必需的.本文考虑了众包系统中几个常用的操作符:CFILL(请求大众填写数据库中缺少的值);CSELECT(要求大众筛选满足某些约束的项);CJOIN(根据某些条件利用大众匹配项);CSORT(根据条件对选择进行排序).针对SQL语言的局限性,采用一种多目标蚁狮优化的查询优化方法,该方法以延迟和查询成本作为目标函数,在给定用户定义的预算约束情况下,找到低延迟的查询计划,从而很好地平衡用户的成本和时间要求.其中,优化查询涉及的成本为所有操作符的总体成本.
本文考虑两个优化目标,第一个仅考虑货币成本:给定一个查询Q,目的是找到一个使货币成本最小的查询计划PQ*
由于目标1下的最优计划可能需要很长时间才能完成,因此需要引入第二个目标,该目标考虑了延迟,目的是在用户提供成本预算下找到一个低延迟的查询计划:给定一个查询Q和成本预算C,它找到一个查询计划PQ*
式(1)、式(2)中:cost和latency分别表示查询计划PQ的查询成本和延迟时间.如果有多个延迟最小的计划,它将找到成本最低的计划.
本文算法提供了一个优化框架.该算法以众包查询Q和成本预算C作为输入,并生成优化的查询计划P*.算法考虑以下两种情况:如果未指定成本预算,则以成本最小化为目标搜索Q的查询计划.否则,算法将以成本限制的延迟最小化为目标函数.优化框架分为4个主要步骤:收集数据生成数据库,生成用户查询、优化用户查询以及将其应用于众包系统.
-
在基于查询的众包系统初始阶段,本文采用输入数据为加州大学欧文分校(UCI)汽车数据集内的数据[10].对于UCI数据集,首先使用数据集中的205辆汽车参数来生成车辆之间的关系;其次将VEHICLE中的每个元组复制20次来生成关系IMAGE,并添加颜色和质量这两个属性,其值是随机生成的.同理,将VEHICLE中的每个元组重复10次生成关系REVIEW,并添加具有随机生成的值的属性情感.在数据集UCI上实现一个模拟众包环境,此环境具有UCI的完整数据库知识.当点击到达时,它会搜索完整的数据库并将正确的答案返回给众包执行者.
-
数据收集后,将收集的数据以SQL格式存储.由于存储的SQL数据结构复杂性不断增长,使得检索所需数据的时间也随之增加.目前,手工编写更复杂文档的查询是一项非常容易出错且繁琐的任务.这些问题尤其在数据仓库中被引起关注,在数据库中文档从不同的来源收集,其结构略有不同.因此,需要一种有原则的方法来协助用户建立查询.
在所提出的方法中,使用关系数据模型.首先,数据被指定为一组关系R={R1,R2,…,R|n|},这些关系可以由操作人员指定,并且能够被众包用户查询.每个关系Ri包含一组描述元组性质的属性{A1i,A2i,…,Ami}.与传统数据库不同,在执行众包之前元组的某些属性是未知的.在查询计划中,应用SELECT,JOIN和FILL这3种类型的运算符,然后使用蚁狮优化器执行查询优化,以便为查询检索提供更好的解决方案.蚁狮优化算法是一种基于种群的算法,它有助于确定随机解集的最优解.当用户遇到困难时,查询优化器能够给出问题的解决方案.这样可以提高效率,并为问题提供更好的解决方案.
-
蚁狮优化算法(ant lion optimization,ALO)是一种群智能优化算法[11],该算法模拟了自然界中蚁狮捕食蚂蚁的行为活动,ALO算法具有调节参数少、寻优精度高、不易陷入局部最优等优点.蚁狮优化算法中具有蚂蚁和蚁狮两个群体,寻优过程可分为蚂蚁随机游走、蚁狮建立陷阱、蚂蚁落入陷阱、蚁狮捕捉猎物和重建陷阱5个步骤.蚂蚁随机游走时的公式可以定义为
式(3)中:n表示最大迭代次数,t表示随机游走的步骤,cs表示计算累积和. r(t)表示随机函数,其定义为
式(4)中:rand表示在(0,1)内均有分布的随机数.为了保证蚂蚁在可行域范围内行走,将蚂蚁的随机游走行为归一化处理
式(5)中:cit和dit分别表示蚂蚁第i分量在第t次迭代时的最小值和最大值,ai和bi分别为蚂蚁第i分量的最小值和最大值.同时,蚂蚁随机游走也受到蚁狮陷阱的影响,是在选定的蚁狮周围运动.
式(6)中:Antlionjt表示第j个蚁狮在第t次迭代时的位置,ct和dt分别为第t次迭代时的最小值和最大值.
ALO算法为了提高收敛速度,寻求得到最优解,将蚂蚁随机游走的范围随迭代次数增加而逐渐降低.
式(7)中:
$I = 1 + {10^\omega } \times \frac{t}{n}$ ,ω表示随迭代次数而动态调整的参数.蚁狮捕食运动到陷阱底部的蚂蚁后,根据式(2)中多目标适应度值更新位置为
式(8)中:Antit表示第i个蚂蚁在第t次迭代时的位置.蚁狮更新完位置后,重新构造陷阱,用于捕获下一只蚂蚁.选取并保存每次迭代时的最佳蚁狮作为精英蚁狮,精英蚁狮在ALO算法迭代过程中可以影响所有蚂蚁的活动.为了避免算法陷入局部最优,ALO算法通过轮盘赌选择和随机游走确定蚂蚁的位置,即
式(9)中:RAt表示由轮盘赌在第t次迭代选择的蚁狮周围随机游走产生的值,REt表示在第t次迭代精英蚁狮周围随机游走产生的值.
2.1. 数据收集
2.2. 查询优化
2.3. 蚁狮优化算法
-
为了验证算法的性能,所有实验在MATLAB 2018a中进行,运行环境配置为Net Beans 6.2版本,3.0 GHz英特尔i5处理器,2 TB硬盘和16 GB RAM工作站.为了评估本文算法的效率和有效性,从精度、货币成本和延迟等方面考察本文方法的性能,并将实验测试结果与A-BAT算法[7]、WOA算法[9]和CDB算法[12]等查询优化算法进行比较.
为了验证选择、联接、复杂查询和排序等几个常用操作符在众包查询优化算法中的有效性,在实验中使用线性价格函数f=b+wx,其中b和w分别表示基本费用和增量费用.对于CSELECT,CJOIN和CSORT,将b和w都设置为 $ 0.005,而对于CFILL,将b和w分别设置为${\rm{\$ }}\;0.01$ 和 ${\rm{\$ }}\;0.02$.
-
绩效衡量被定义为对结果的衡量,它提供了一个关于系统有效性和效率的可靠信息.系统输入值和输出值之间的关系可以通过使用精度、货币成本和延迟等性能指标来评估.
计算众包系统中查询优化货币成本的公式用数学表示为
式(10)中:cost(o)表示执行每个运算符的成本.
由于众包需要时间,因此自然会引入延迟来量化查询评估的速度,本文将查询计划PQ的等待时间L(PQ)衡量为PQ众包执行中使用的迭代次数.同时,如果存在垃圾邮件发送者或恶意工作人员,众包可能会产生相对较低质量的结果,甚至产生噪音.因此,精度被视为衡量众包结果质量的另一个重要性能指标.
-
在实验分析中,利用UCI汽车数据库对本文算法与现有算法进行了性能评价比较.表 1和表 2给出了不使用预算和使用预算时本文算法与其他算法的测试结果.
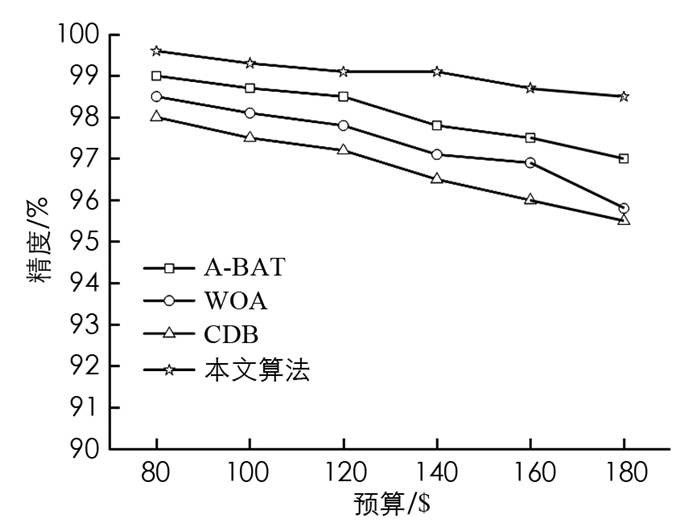
从表 1中可以看出,选择条件的数量为2~6个,并且为每个选择条件随机创建10个查询并计算平均成本.在这种情况下,本文方法性能最高,在所有设置中产生了最低的成本.在表 2中,对本文方法进行了预算限制评估,预算限制在80~180$范围内,改变众包的预算是为了要求大众在预算限制内找到尽可能多的答案,在这里查询被考虑为6个选择条件,并与A-BAT、WOA和CDB的查询优化器进行比较.首先按选择顺序的升序排列选择条件,然后将其随机打包分组.从表 2中可以看出,本文提出的多目标优化算法具有更低的代价.同时,图 1给出了不同预设限制下的精度对比,从图 1中可以看出,在每种预算下,所有优化方法的精度都在95%以上,都能够达到优化的目的,但是通过对比发现,本文算法的精度最高,几乎达到99%的精度,优于其他方法.
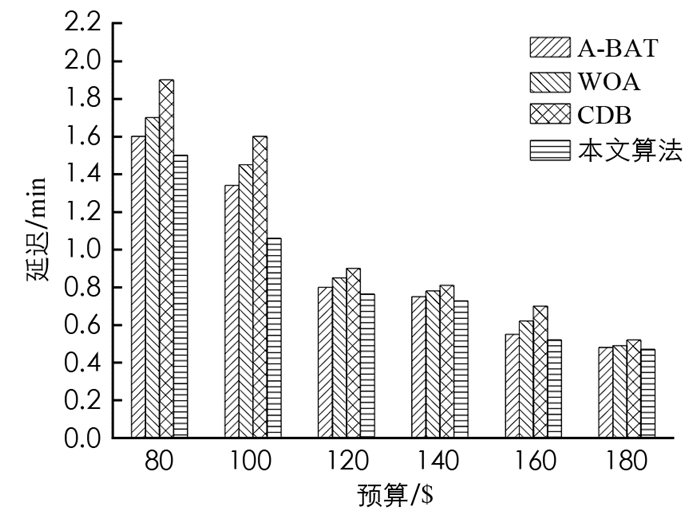
图 2给出了在预算限制条件下不同算法的延迟结果.在这个实验中,考虑了6种选择条件下的查询,从图 2中可以看出,本文所提出的多目标优化算法显著减少了延迟,这是由于本文所提出的技术优势产生了最佳分组,它可以明智地确定哪些条件可以分组以减少延迟,并以最佳顺序应用这些条件.
本文针对众包系统查询优化中存在的查询成本高和延迟时间长的问题,提出一种基于多目标蚁狮优化器的查询优化方案,该方案以最小化延迟和查询成本作为目标函数,通过优化器找到满足固定预算条件下的低延迟查询计划,如果存在多个延迟最小的计划,则选择成本最低的计划作为最佳查询计划.本文所提出的方案考虑了成本和延迟直接的平衡并支持选择、联接和复杂查询等多个众包操作符.实验结果表明,本文所提出的众包查询优化方案比其他算法更有优势,明显降低了查询优化的成本.



 下载:
下载: