高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

基于Q图的M(t)/M/C服务台配置优化

,  ,  , 

上一篇

下一篇

高琦, 宫丽芳, 武艳华, 等. 基于Q图的M(t)/M/C服务台配置优化[J]. 西南大学学报（自然科学版）, 2022, 44(4): 206-212. doi: 10.13718/j.cnki.xdzk.2022.04.024
引用本文: 高琦, 宫丽芳, 武艳华, 等. 基于Q图的M(t)/M/C服务台配置优化[J]. 西南大学学报（自然科学版）, 2022, 44(4): 206-212. doi: 10.13718/j.cnki.xdzk.2022.04.024
shu
GAO Qi, GONG Lifang, WU Yanhua, et al. Staffing Level for Dynamic M(t)/M/C: A Q-Chart Method[J]. Journal of Southwest University Natural Science Edition, 2022, 44(4): 206-212. doi: 10.13718/j.cnki.xdzk.2022.04.024
Citation: GAO Qi, GONG Lifang, WU Yanhua, et al. Staffing Level for Dynamic M(t)/M/C: A Q-Chart Method[J]. Journal of Southwest University Natural Science Edition, 2022, 44(4): 206-212. doi: 10.13718/j.cnki.xdzk.2022.04.024
shu

基于Q图的M(t)/M/C服务台配置优化

  • 山东财经大学 统计学院，济南 250000

  • 基金项目: 国家自然科学基金项目(11901347)；山东自然科学基金项目(ZR2019MA035，ZR2020MA036)
详细信息
    作者简介:

    高琦，硕士研究生，主要从事排队系统的统计推断方面的研究 .

    通讯作者: 戴洪帅，教授

  • 中图分类号: C931.1; O226

Staffing Level for Dynamic M(t)/M/C: A Q-Chart Method

  • School of Statistics, Shandong University of Finance and Economics, Jinan 250000, China

  • 摘要: 排队问题随处可见，如何科学有效地对排队拥堵状况进行监控，合理配置资源具有重要的理论和现实价值. 与平稳模型相比，动态排队模型由于其时变特征，适用性更广. 本文根据逐段平稳和M/M/C模型的相关理论，构建了基于Q图的动态M(t)/M/C模型. 该模型利用Q控制图对过程中的到达率λ进行实时监测，根据变点对到达过程进行分段，进而优化服务台的配置问题. 随机模拟结果表明，该模型具有优良的检测效果，能够使有限的服务台资源得到有效利用. 最后，本文基于收费站数据，进行了实证分析，结果表明该模型可以实时监测到达率的变化情况，从而达到合理安排人工收费车道的目的.
    Abstract: Queueing problems can be seen everywhere. How to effectively monitor queueing congestion and rationally allocate resources have important theoretical and practical values. The study of dynamic queues with time-varying arrival rates has become popular in queueing theory. In this work, we applied the Q-chart to study the staffing level for dynamic queueing system M(t)/M/C. This chart was applied to monitor the arrival rate λ in the process in real time. According to the change points, the process was segmentized to optimize the configuration of service station. Stochastic simulation results show that the method has advantage in improving the utilization rate of the service station. An empirical analysis was conducted in this study.
  • 加载中

  • 图 1  模拟数据的Q控制图

    下载: 全尺寸图片 幻灯片

    图 2  车流量分布与K-S检验图

    下载: 全尺寸图片 幻灯片

    图 3  车流量的Q控制图

    下载: 全尺寸图片 幻灯片

    表 1  模拟数据

    ni xi ni xi ni xi ni xi ni xi ni xi ni xi ni xi
    4 5 4 11 4 8 4 6 4 5 4 7 4 9 5 8
    4 6 4 8 4 6 4 9 4 6 4 7 4 4 5 19
    4 7 4 8 4 9 4 11 4 2 4 7 4 15 5 21
    4 10 4 3 4 7 4 5 4 6 4 4 4 16 5 14
    4 5 4 5 4 8 4 8 4 10 4 9 5 20 5 15
    4 10 4 4 4 14 4 4 4 6 4 8 5 17 5 18
    下载: 导出CSV

    表 2  Q分位数

    i Qi i Qi i Qi i Qi i Qi i Qi i Qi i Qi
    1 -0.705 7 -0.045 13 0.782 19 1.246 25 -2.021 31 0.141 37 2.681 43 3.018
    2 0.484 8 -1.854 14 0.068 20 -0.849 26 -0.232 32 -1.024 38 2.871 44 1.155
    3 -1.116 9 -0.857 15 0.424 21 0.285 27 1.166 33 0.873 39 3.822 45 1.394
    4 0.743 10 -1.158 16 2.237 22 -1.211 28 -0.250 34 0.514 40 2.174 46 2.126
    5 0.921 11 0.426 17 -0.427 23 -0.750 29 0.134 35 0.845 41 -0.469 47 NA
    6 -0.086 12 -0.289 18 0.643 24 -0.329 30 0.138 36 -1.034 42 2.624 48 NA
    下载: 导出CSV

    表 3  模拟结果对比表

    λ C ρC W
    算术平均 2.558 12 0.213 0.105 9
    节点一 1.757 11 0.146 0.097 6
    节点二 3.359 13 0.240 0.093 9
    下载: 导出CSV
  • [1] 唐加山. 排队论及其应用[M]. 北京: 科学出版社, 2016.
    [2] LAKSHMI C, LYER S A. Application of Queueing Theory in Health Care: a Literature Review[J]. Operations Research for Health Care, 2013, 2(1-2): 25-39. doi: 10.1016/j.orhc.2013.03.002
    [3] LIU Y N. Many-Server Queues with Time-Varying Arrivals, Customer Abandonment and Non-Exponential Distributions[D]. New York: Columbia University, 2011.
    [4] GREEN L, KOLESAR P. The Pointwise Stationary Approximation for Queues with Nonstationary Arrivals[J]. Management Science, 1991, 37(1): 84-97. doi: 10.1287/mnsc.37.1.84
    [5] HE B X, LIU Y N, WHITT W. Staffing a Service System with non-Poisson non-Stationary Arrivals[J]. Probability in the Engineering and Informational Sciences, 2016, 30(4): 593-621. doi: 10.1017/S026996481600019X
    [6] 李建国, 张海飞, 周璐婕, 等. 基于改进遗传算法的立体车库布局对比及服务资源优化[J]. 西南大学学报(自然科学版), 2019, 41(4): 139-148. doi: http://xbgjxt.swu.edu.cn/article/doi/10.13718/j.cnki.xdzk.2019.04.020
    [7] 邱春红. 云计算中虚拟机簇的优化分配[J]. 西南师范大学学报(自然科学版), 2021, 46(1): 44-49. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-XNZK202101008.htm
    [8] BHAT U N, RAO S S. A Statistical Technique for the Control of Traffic Intensity in the Queuing Systems M/G/1 and GI/M/1[J]. Operations Research, 1972, 20(5): 955-966. doi: 10.1287/opre.20.5.955
    [9] CHEN N, ZHOU S Y. CUSUM Statistical Monitoring of M/M/1 Queues and Extensions[J]. Technometrics, 2015, 57(2): 245-256. doi: 10.1080/00401706.2014.923787
    [10] QI D Q, LI Z H, ZI X M, et al. Weighted Likelihood Ratio Chart for Statistical Monitoring of Queueing Systems[J]. Quality Technology & Quantitative Management, 2017, 14(1): 19-30.
    [11] 王颖俐. 基于M/M/c/∞排队模型分析超市收银台数量[J]. 太原师范学院学报(自然科学版), 2015, 14(2): 8-10, 27. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-SJYX201502002.htm
    [12] SYSKI R. Fundamentals of Queueing Theory[J]. Technometrics, 1999, 41(1): 76-77.
    [13] 权政, 赵玲玲, 徐滨, 等. 面向大规模定制的改进型AEWMAQ控制图应用研究[J]. 机床与液压, 2021, 49(24): 8-12.
    [14] QUESENBERRY C P. SPC Q Charts for a Binomial Parameter P: Short or Long Runs[J]. Journal of Quality Technology, 1991, 23(3): 239-246. doi: 10.1080/00224065.1991.11979329
    [15] GREEN L V, KOLESAR P J, WHITT W. Coping with Time-Varying Demand when Setting Staffing Requirements for a Service System[J]. Production and Operations Management, 2007, 16(1): 13-39. doi: 10.1111/j.1937-5956.2007.tb00164.x
    [16] 姬杨蓓蓓, 周金凤. 基于成本分析的高速公路收费站车道配置研究[J]. 重庆交通大学学报(自然科学版), 2018, 37(1): 85-91. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-CQJT201801014.htm
    [17] 曲明革. 高速公路出入口收费车道数研究[J]. 公路, 2012, 57(5): 262-267. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-GLGL201205060.htm
    [18] 黄虎, 柯华, 王晶. 基于逆加权参数估计方法的改进型Q控制图研究[J]. 系统工程学报, 2016, 31(4): 568-574. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-XTGC201604014.htm
  • 加载中
图( 3) 表( 3)
计量
  • 文章访问数:  1095
  • HTML全文浏览数:  1095
  • PDF下载数:  76
  • 施引文献:  0
出版历程
  • 收稿日期:  2021-03-27
  • 刊出日期:  2022-04-20

基于Q图的M(t)/M/C服务台配置优化

    通讯作者: 戴洪帅，教授
    作者简介: 高琦，硕士研究生，主要从事排队系统的统计推断方面的研究
  • 山东财经大学 统计学院，济南 250000
  • 收稿日期:  2021-03-27
基金项目:  国家自然科学基金项目(11901347)；山东自然科学基金项目(ZR2019MA035，ZR2020MA036)

摘要: 排队问题随处可见，如何科学有效地对排队拥堵状况进行监控，合理配置资源具有重要的理论和现实价值. 与平稳模型相比，动态排队模型由于其时变特征，适用性更广. 本文根据逐段平稳和M/M/C模型的相关理论，构建了基于Q图的动态M(t)/M/C模型. 该模型利用Q控制图对过程中的到达率λ进行实时监测，根据变点对到达过程进行分段，进而优化服务台的配置问题. 随机模拟结果表明，该模型具有优良的检测效果，能够使有限的服务台资源得到有效利用. 最后，本文基于收费站数据，进行了实证分析，结果表明该模型可以实时监测到达率的变化情况，从而达到合理安排人工收费车道的目的.

English Abstract

    全文HTML

  • 开放科学(资源服务)标识码(OSID):

  • 排队系统的研究大体可分为3个方面：①性能分析；②统计推断；③资源配置[1]. 在排队模型的研究中，目前学者们通常假设顾客的到达率是不变的，具有平稳性. 但在很多情况下，如医院急诊室[2]，顾客的到达具有时变的特征，文献[3]指出若到达率只是偶尔非平稳，利用平稳排队模型分析系统的性能指标，得到的效果并不是最优的. 文献[4]指出即使到达率只是适度的不平稳，若利用平稳排队模型拟合系统，也会造成性能指标的严重低估，因此，逐段近似的方法成为研究非平稳排队模型的一类重要方法. 最近几十年，具有时变到达率的排队模型的资源配置问题成为学者们的研究热点之一. 文献[5]研究了非平稳到达过程的一般模型，使用平方根公式建立了服务台配置算法. 文献[6]根据改进的遗传算法建立了有关立体车库的排队模型，该模型可以缓解城市交通的压力，从而可以提升立体车库的服务率. 文献[7]为了实现资源利用效率的最大化，提出了以能量最小化为基础的虚拟机簇分配方法.

    近年来，排队模型的统计控制问题引起了学者们的广泛关注. 文献[8]通过转移概率，给出变点监测的方法，并为M/G/1和GI/M/1模型系统利用率的监测提供了控制限. 文献[9]通过CUSUM表监控排队系统M/M/1队列的服务性能，并与几种替代方法进行了对比. 考虑到数据的自相关性，文献[10]提出了一种基于加权似然比检验的WLRT控制图，该控制图能有效地监控排队系统的性能指标，尤其是对于M/M/1队列系统利用率的监控.

    目前在排队论的研究中，学者们通常把排队系统的性能监控和资源配置优化问题分开考虑. 另外，现实中很多排队系统的服务效率主要与服务台本身有关，如超市收银台的服务速率主要与收银员的熟练程度有关[11]. 基于以上考虑，本文将系统性能的监控和服务台配置综合考虑，基于Q图研究M(t)/M/C模型服务台优化配置的问题.

1.   理论基础

  • 在M(t)/M/C模型中，到达过程服从Poisson分布，但此时到达率不再恒定而是关于时间t的函数. 本文采用M/M/C模型和Q图技术对动态M(t)/M/C排队模型到达率的变化进行检测，从而优化服务台的配置问题，下面对符号术语进行简要的介绍.

    • 1.1.   M/M/C

  • 本文采用逐段近似的方式优化M(t)/M/C模型的服务台配置问题，通过监测变点对排队系统进行合理的分段，每段近似服从平稳的M/M/C模型，并利用该模型研究相关问题. 在M/M/C模型中，顾客的到达速率服从参数为λ的泊松分布，服务时间服从参数为μ的指数分布，服务台的数量为C，等待空间和客源数量为无穷大，服务规则是先到先服务[12]. 其中，ρc=λ/(Cμ)表示系统的服务强度，一般来说只有当ρc＜1时才能保证系统的平稳运行. W是用来刻画顾客等待时间的参数，其平均值为E(W|W＞0)，概率为P(W≤T|W＞0). 进一步有

    • 1.2.   Q图

  • 传统控制图通常只能监测服从标准正态分布的数据，对于服从泊松过程的数据其监测性能较差. 文献[13]将Q统计量应用于自适应移动加权平均控制图中，将参数值进行标准化处理，对常规控制方法进行了改进. 文献[14]也对Q图进行了性能的改进，在绘制泊松属性图的工作中采用了近似标准化的控制图，通过泊松分布进行变换，使数据近似标准化，并给出检测泊松参数的Q图技术. 因此，本文采用改进后的Q图来检测排队系统到达速率的变化.

2.   模型

  • 在M(t)/M/C模型中，顾客的到达服从强度为λ(t)的非齐次Poisson分布. 为了对队列的到达速率进行实时监测，本文构建了基于Q控制图的监测方法，通过逐段平稳的M(t)/M/C模型对其服务台配置问题进行研究.

    • 2.1.   Q统计量

  • 本文首先对到达率λ(ti)进行估计并检测变点，根据检测出的变点时刻将排队队列分为i(i=1，2，…，m)段，每段的时间记为ti，经过ni次观测，顾客的到达速率为λ(ti)，到达速率随着ni的变化记为niλ(ti). 当每段中顾客的到达速率和到达人数均相同时，ni和λ(ti)为常数，即ni=n，λ(ti)=λ0，计算可得每段顾客人数的均值为nλ0，方差为nλ0，利用传统的3σ控制图构造上下控制限，则

    每段所需观测的最小样本数如下所示：

    当λ(ti)随时间ti变化时，上下控制限的误差增大，控制图的灵敏度降低. 为了提高控制图的检测性能，本文将服从泊松分布的顾客数量的观测值xi转化为可以在标准化正态Q图上绘制的值，Xi是不同时段所有顾客数量的观测值xi的和，即Xi=x1+x2+…+xi，Ni是整个系统的总观测次数，ni是该时段观测的总次数，即Ni=n1+n2+…+ni. 将x1，x2，…，xi转化为Q统计量，通过下式给出相应的变换：

    • 2.2.   服务台配置优化算法

  • 本文利用逐段平稳方法研究M(t)/M/C模型的服务台配置优化问题. 利用Q图检测到达速率λ的变化，将发生变点的时刻记为t1，在t1处对到达过程进行分段处理，并分别估计出每段的到达速率λ1和λ2的值. 若估计得到的λ2和λ1相等，则说明产生了误报，此时是一个伪检验，不需要采取任何措施；若得到的λ2与λ1相差较大，表明到达速率λ发生了变化，收到报警信号后，通过到达率λ2与λ1构造新的到达率λ的值，根据平稳模型对服务台的数量进行调整，从而优化系统中顾客的拥堵程度和等待时间.

    具体算法如下：

    ① 利用Q图检测整个排队过程中到达率的变点，得到发生变点的时刻t1和到达率的估计值λ1；

    ② 基于到达率λ1和给定的延迟概率α，利用M/M/C模型的相关性质，计算服务台的数量C，即

    通过上式可知，服务台数量C满足

    ③ 在时刻t1之后，基于到达率的估计值λ2，若λ1=λ2，则将检测下一个变点，若λ1≠λ2，则重复步骤②计算该段服务台的最优配置；

    ④ 重复上面的步骤，直至周期结束.

3.   模拟实验

  • 本节设计了随机模拟实验证明该模型的理论优势. 首先选取i个样本观测值，对λ设定不同的参数来模拟Q图的监测过程. 本文共选取了48个样本点，即i=1，2，…，48. 根据式(3)计算得到样本的最小值为4，因此，可将前40个样本观测值每个节点的观测次数ni=4，后8个样本观测值的每个节点的观测次数ni=5. 到达速率初始值设为λ1=1.7，λ2=3.4，服务速率设为μ1=μ2=1. 假定i=39时，到达速率λ发生变化，即前39个观测点服从λ1=1.7的泊松分布，后9个观测点服从λ2=3.4的泊松分布. 模拟得到系统中每个节点的观测次数ni和人数xi的取值如表 1所示.

    经计算可得

    通过式(4)，计算得到的Q分位数结果如表 2所示.

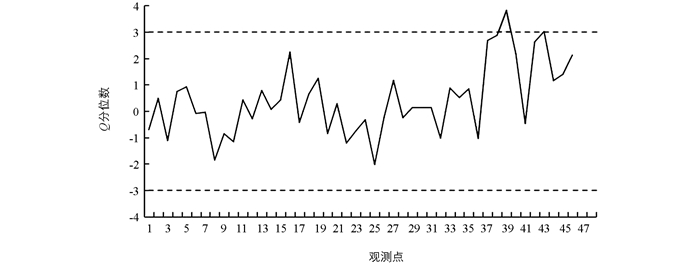
    在Q控制图中描绘出各模拟点的值，从图 1可以看出不同点对应的Q分位数的波动. 其中，第39个点对应的分位数超出了控制限[-3, 3]的范围，系统发出警报，表明该控制图检测出了λ的变化.

    由于式(4)中的二项分布是泊松分布的最小方差无偏估计[14]，因此可以用二项分布的概率pi=ni/Ni来估计到达速率λi，得到λ1=1.756 998，λ2=3.358 514. 其中，估计得到的λ1和λ2相差较大，说明没有发生误报. 第39个样本点是发生变化的点，根据逐段平稳的性质对系统进行分段处理，将前38个样本观测点规划到前一个节点内，后10个样本观测点规划到后一个节点内，得到权重ω1和ω2的值.

    因此，根据优化后模型的权重计算到达速率λ的值为

    通过算术平均计算得到的到达率λ′的值为

    基于Green等标准的服务水平优化目标[15]，本文设置延迟概率不超过80%，即α=0.8，可以得到等待时间小于T的概率，

    为了使顾客的等待时间相对较少，令T=10/60=1/6，由此计算出满足此条件的服务台数量为C≤11.74，这里服务台个数取整为12. 由式(1)可以得出排队系统中每一位顾客的平均等待时间为W=0.100 9. 同理根据λ′计算得出其服务台数量和等待时间分别为C′≤12.21，W′=0.105 9，服务台个数取整为12. 为了能够合理地分配总的服务台个数，根据系统的逐段平稳性质得到第一个节点和第二个节点所需要的服务台数量为

    通过模拟，根据C1和C2的取值，可以更加合理地安排不同时段的服务台数量，第一段安排服务台数量为11，等待时间W1=0.097 6，第二段安排服务台数量为13，等待时间W2=0.093 9.

    2种模型计算的结果如表 3所示.

    对比这2种模型所需服务台的数量和顾客的等待时间，研究发现优化之后的模型更加实用，主要体现在以下2个方面：

    ① 从顾客角度来说，优化之后的模型可以减少每一位顾客的等待时间，进而可以提高顾客的满意度.

    ② 从资源利用的角度来说，优化后的模型能够根据顾客到达率的变化合理安排服务台的个数，可以更为有效地利用服务资源，完成资源的优化配置.

4.   实证分析

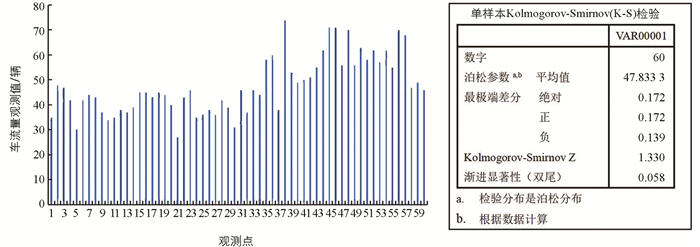
  • 本文选取与现实生活密切相关的高速公路人工收费车道问题进行实证分析. 随着车辆的不断增加，高速公路收费站处会出现到达车辆不能及时得到服务的状况，为了解决车辆排队的拥堵现象，文献[16-17]分别采用M/M/N和M/G/K模型系统描述收费站的排队情况. 本文以山东省某收费站为例，利用上述模型对车流量进行监测，并合理安排人工收费车道的数量. 该收费站共有8个服务台，3条ETC通道，5条人工通道，由于ETC通道全天候开放，故只对人工通道的车流量进行观测并记录，其中工作人员实行三班轮换制，即每8 h换班一次. 由于每周的车流量数据具有一定的周期性，因此每周只选取一天进行观测，连续观测6周，于每周三6：00-21：00每15 min记录一次观测值，发现同一时段的观测值相差不大，随机选取收费站某天的车流量数据进行实证分析.

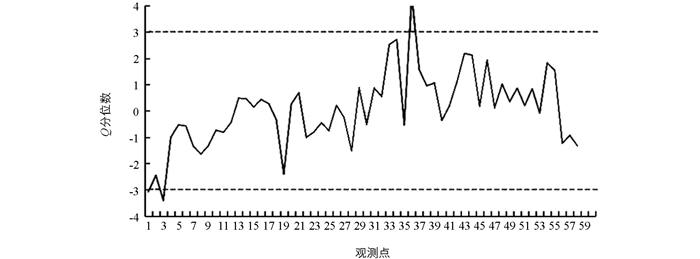
    各时段车流量数据共计60个观测值，其分布直方图如图 2所示. 为了对各时段车流量数据的分布进行研究，采用K-S检验法，由图 2可知P值为0.058，因此该数据近似服从泊松分布. 其中前40个观测值的ni=4，后20个观测值的ni=5，μ≈50辆/h，T=1/6 h，车流量的Q图如图 3所示.

    利用Q图对数据进行监测，图 3表明当第1、第3和第36个点超出控制限时，系统发生报警. 由于开始时系统的不平稳特征[18]，我们排除第1和第3个点的干扰，即无需改变人工收费站的数量. 因此以第36个点作为变点进行分段处理，由极大似然估计可得λ1=165辆/h，λ2=233辆/h，经计算可得，C=5，W≈0.018 h，λ=193辆/h，λ′=199辆/h，C1=4，C2=5. 该模型的计算结果表明，在变点之前安排4个人工收费车道，在变点之后安排5个人工收费车道，相比较于收费站全天候开放5个人工收费车道，优化之后的模型可以及时调整人工收费车道的开放个数，从而能够降低人工费用等各项支出.

5.   结论

  • 本文基于Q控制图对到达速率λ的动态变化进行监控，通过控制图找到异常点，根据变点时刻分段，得到逐段平稳的排队列，利用M(t)/M/C模型的相关理论知识计算出服务台的数量和等待时间，合理地安排服务台数量. 此方法的优点是将变点检测和逐段平稳相结合，从而优化了动态排队模型的服务台配置问题. 本文利用收费站某天的车流量数据进行了实证分析，结果表明，Q控制图能够对动态的车流量数据进行实时监测，检测出车流量变化幅度较大的点. 根据变点计算出各段的人工收费车道数量，进而实时调整服务资源，缓解收费站的拥堵情况，降低收费站人工成本等各类的支出，具有重要的现实意义.

参考文献 (18)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回