矩阵作为数学工具之一，在现代科学中的应用日益突出，在机器学习、图像处理、无人驾驶、电子工程等方面有着非常重要的应用^[10]. 矩阵源起于数的思想，是数的拓展，即数阵. 矩阵与数类似，可以进行运算. 然而，矩阵乘法与数乘相比，过程比较复杂，初学者不理解为什么要这样定义. 在教学中，教师可以通过矩阵乘法被创造的过程讲起，带领学生领悟知识的创造过程，促使学生对知识理解得更加深刻和透彻.

教师通过知识的发生过程了解人类是如何获得某些认识的，从而对学生应该如何领悟这些认识做出更好的再创造，这种方法称为发生教学法. 发生教学法借鉴历史引入主题，保护学生猎奇的天性，通过引导学生重现知识的再发现过程，培养学生的创造力和创新精神. 布鲁纳发现学习理论认为，只有学生自己亲自发现的知识才是真正属于他自己的东西. 教学目的不该是学生记住教师和教科书上所陈述的内容，而是要培养学生发现知识的能力，从而培养学生卓越的智力. 这样学生就好比得到了打开知识大门的钥匙，可以独立前进了.

矩阵加法的定义要求必须是两个同型矩阵才可以施行，只需将对应位置上的元素相加，即可得到两矩阵的和矩阵. 在定义矩阵乘法时，同学们自然地会想到(1)式的定义方法

即将两个同型矩阵对应位置上的元素相乘，得到它们的乘积矩阵. 历史上的确有人曾经这样定义矩阵的乘积，这种乘积称为矩阵的Hadamard乘积^[11].

如今，Hadamard乘积在算法中经常使用，然而在当时的基础数学领域，这种定义方法缺乏实际的应用背景和理论价值，没有被推广开来. 历史有其偶然也有其必然，现在广泛应用的矩阵乘积被称为一般的矩阵乘积，它是由英国数学家阿瑟·凯莱在研究线性变换的复合时提出来的. 矩阵乘积的这一定义推动了矩阵理论的快速发展. 目前，矩阵乘积是矩阵理论中最重要的运算之一.

矩阵的创立是用来解线性方程组问题的，与线性方程组关系非常密切的一类问题即是线性变换问题. 凯莱在研究线性变换的复合时，将线性变换所对应的矩阵之间的运算关系定义为矩阵乘法.

一般矩阵乘法的由来：

1) 线性变换的本质

由变量x₁，x₂，…，x_n到变量y₁，y₂，…，y_m的线性变换

的本质是一个由实数空间$\mathbb{R}^n $到实数空间$\mathbb{R}^m $的映射，即多维空间上的映射，可见这个映射可以将n维空间中的元素映射到m维空间当中. 高等数学中学习过数集上的映射以及映射的复合，学生自然会想知道线性变换的复合是什么样的.

2) 矩阵乘法的定义

根据

计算可得由变量x₁，x₂到z₁，z₂的线性变换

线性变换(4)是先做线性变换(3)，再做线性变换(2)的结果，即是线性变换(2)与(3)的复合，称为(2)与(3)的乘积. 由于线性变换与其系数矩阵是一一对应的关系，3个线性变换所对应的矩阵分别为A，B和C，此时称矩阵C是矩阵A与B的乘积，记作C=AB^[12].

通过让学生观察，总结出矩阵C中元素与A和B中元素之间的关系为

根据(5)式的运算规则，分组讨论，共同解决以下问题：

1) 是否任意两个矩阵都能施行乘法运算?

2) 请确定乘积矩阵C中元素的构成和C的形式.

通过学生分享讨论结果，使学生掌握矩阵能相乘的条件，即左矩阵的列数等于右矩阵的行数. 相乘的计算方法为左行右列法——矩阵乘积元素c_ij等于左矩阵的第i行与右矩阵的第j列对应元素乘积之和. 乘积矩阵的行列数——左矩阵的行数为乘积矩阵的行数，右矩阵的列数为乘积矩阵的列数等. 最后共同总结出矩阵乘法的一般定义：

定义1  设A=(a_ij)是一个m×p矩阵，B=(b_ij)是一个p×n矩阵，C=(c_ij)，如果

则称矩阵C=(c_ij)_m×n为矩阵A与矩阵B的乘积，记作C=AB.

传统的教学理念认为学生知识、技能的获得均来于教师，所以教师在授课时往往不考虑学生的感受，将知识与技能满堂灌. 近年来一直在提倡应以学生为主体、教师为主导的方式进行教学^[13]. 通过学生课堂上讨论并分享讨论结果的方式，充分发挥学生在课堂上的主体作用，增加学生在发现知识过程中的学习投入和情感投入，提高学生学习数学的内在动机. 学生在讨论中碰撞出知识的火花，一步步打开真理的大门，深刻掌握知识点的同时，提高语言表达能力和知识讲授能力，增强学好数学的勇气和自信心.

在学习矩阵加减法时，我们是通过与实数的加减法比较^[14]引出的，其运算规律与实数的加减法运算规律较为一致，由此继续引导学生思考矩阵乘法的运算规律又是如何？是否仍然和实数乘法的运算规律一致？引导学生总结出矩阵乘法的运算规律.

在说明矩阵乘法一般不满足交换律和消去律时，最直接的方法就是举反例.

例1  设

计算AC，AB和BA.

由AC=O，可以进一步说明矩阵相乘不满足消去律.

从计算结果中可知，AB≠BA，即矩阵乘法不满足交换律. 矩阵乘法的这一特点与数的乘法有很大的区别，为什么会有这样的结果呢？这里从矩阵乘法的本质来说明：

例1中矩阵A所对应的线性变换为平面上任意一个向量关于x轴的投影变换，即

B所对应的线性变换为绕原点逆时针旋转90°的旋转变换，即

其中$\varphi = \frac{{\rm{ \mathit{ π} }}}{2} $.

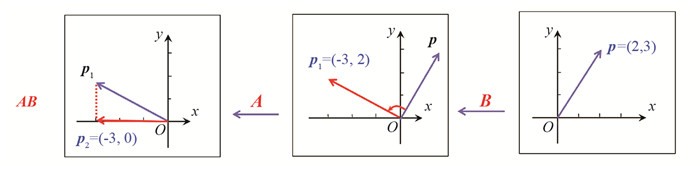
下面考虑A与B所对应的线性变换对平面$\mathbb{R}^2 $中任意向量复合作用后的效果，不妨取$\mathbb{R}^2 $中的一个元素p=(2，3)(p在平面中可以代表向量).

AB所对应的复合线性变换作用于p，指先将向量p绕原点逆时针旋转90°，再对得到的向量p₁向x轴作投影，变换后的结果为p₂=(－3，0)(见图 1)；

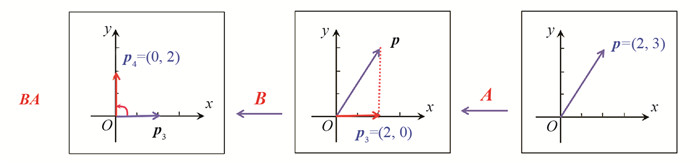
BA所对应的复合线性变换作用于p，指先对向量p作x轴的投影，得到向量p₃，再绕x轴逆时针旋转90°，结果为p₄=(0，2)(见图 2).

因此线性变换复合的顺序不一样，结果也往往不一样，所以，矩阵乘法运算一般不满足交换律. 此处，AB称为A左乘B，BA可称为A右乘B. 矩阵乘法运算满足分配律，但是由于其不满足交换律，分配律区分为左分配律和右分配律.

在解二元一次方程组和三元一次方程组的过程中，发现方程组的系数对方程组的解起决定性作用. 事实上，大约在公元前1世纪，我国的《九章算术》的“方程”章中就叙述了一个三元线性方程组的解法，当时用算筹将未知数的系数和常数项排列成一个长方阵，运用遍乘直除算法求解，这就是矩阵最早的雏形，遍乘直除算法就是现今矩阵的初等变换. 以算法体系为特征的中国传统数学，为世界数学的发展开创了新观念^[15].

行列式和矩阵都是伴随着解线性方程组而产生的，都是通过对方程组的系数进行处理而达到解方程的目的. 行列式用来解未知量个数与方程个数相等的线性方程组. 1850年，西尔维斯特在研究未知量个数与方程个数不相等的线性方程组时，行列式不能使用，提出了矩阵一词，表示一项由m行n列元素组成的矩形阵列，这是最早矩阵一词的使用. 根据矩阵乘法的运算规则，含有n个未知数，m个方程的线性方程组

可以写成矩阵乘法的形式. 令

则线性方程组可记作Ax=b. 此式可看成是矩阵相乘的特殊形式. 其中A称为矩阵方程的系数矩阵，x称为未知数矩阵，b称为常数项矩阵. 未知量是矩阵的方程称为矩阵方程.

这一形式可以推广到更一般的情形，令

矩阵方程AX=B可看作是由系数矩阵相同的p个线性方程组组成的. 求矩阵方程的解是后续课程中的重要内容. 矩阵乘法的一般定义，将求线性方程组的解的问题转换成了求矩阵方程的问题，极大地简化了线性方程组的求解问题，这也是矩阵乘法在矩阵论中相当重要的原因.

利用矩阵乘法将线性方程组写成矩阵方程的形式，只需对矩阵进行相应的处理即可方便快捷地解决线性方程组的解的问题. 启发学生在解决问题时要善于抓住问题的本质，做到事半功倍.

矩阵乘法在图像处理中有着非常重要的应用. 我们对图片的数字化处理实质上就是对图片所对应的矩阵进行相应的运算. 为了理解这点，以一个简单的例子说明.

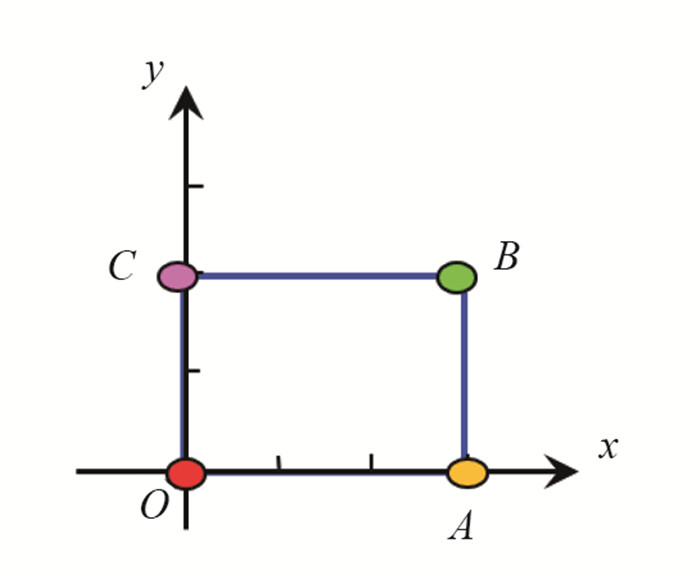
例2  将图 3中矩形的4个顶点绕原点逆时针旋转90°，

点O，A，B，C所对应的点坐标作为列向量构成的矩阵为

绕原点逆时针旋转90°的线性变换所对应的矩阵为

对O，A，B，C这4个点同时做线性变换，就是用R左乘G，计算RG，得到旋转后的4个点构成的矩阵为

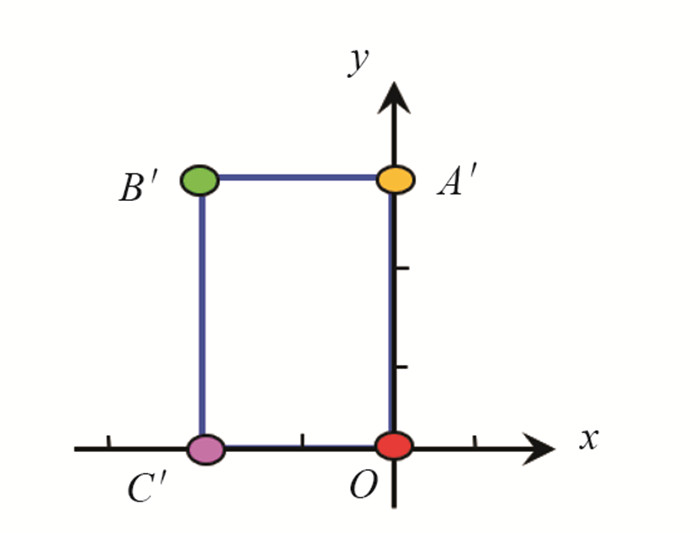
旋转后的4个点记为O，A′，B′，C′，对应图像为

注意，此处仅仅是将矩形的4个顶点进行了旋转.

一般地，对一张图片进行旋转，本质上是用旋转变换所对应的矩阵左乘图片所对应的像素矩阵. 具体地用Matlab软件进行演示，如图 5，即是将战斗机图片逆时针旋转30°，

另外，利用矩阵的运算可以实现对图片的剪切、伸缩以及图片信息的隐藏等. 将相应的Matlab程序发送到智慧平台，供学有余力的学生课后学习和操作. 利用人们常用的图像编辑，引起学生学习的兴趣，使学生认识到矩阵乘法运算的广泛应用，更加重视矩阵理论的学习.

本文利用发生教学法，根据学生认知规律，从矩阵乘法的创立过程出发，对矩阵乘法的内容进行了教学设计，带领学生重新经历矩阵乘法的创造过程，理解矩阵乘法的本质是线性变换的复合. 通过课堂小组讨论，总结得出矩阵乘法运算规则和运算规律的特点，从本质出发阐述矩阵乘法一般不满足交换律的原因. 这个过程，不仅是学生掌握数学知识的过程，更是学生发展创造力，培养科学精神的过程. 而后分析了线性方程组与矩阵方程之间的关系，让学生进一步理解了矩阵乘法运算的现实意义. 最后从学生常用的图像处理的角度探讨了矩阵乘法的应用，让学生深刻体会到知识来源于实践，概念的创造是用来解决问题的，不是凭空创造出来的. 通过Matlab的实验操作和课后练习，让学生熟悉数学软件的使用，体会矩阵理论和数学软件的强大应用，培养学生的抽象思维和逻辑思维，加强学生们未来学以致用、学以善用的综合能力和水平^[16].