-
开放科学(资源服务)标志码(OSID):

-
自党的十八届五中全会习近平总书记提出“创新、协调、绿色、开放、共享”五大发展理念以来,为实现创新驱动发展、建成创新型国家,我国出台了如《“十三五”国家科技创新规划》等一系列政策文件,以扶持高新技术企业的发展. 党的二十大报告进一步指出,要“构建优质高效的服务业新体系,推动现代服务业同先进制造业、现代农业的深度融合”. 高技术服务业作为高技术产业与现代服务业融合的产物,成为中国产业发展的重要方向. 在创新驱动发展背景下各地区高技术服务业从业者数量增幅显著[1]. 那么,这种增加是否以牺牲其他行业劳动力的就业机会为代价,抑或会催生新的产业间合作、推进产业间的融合,从而使得其他行业从业人员的就业机会也增加?
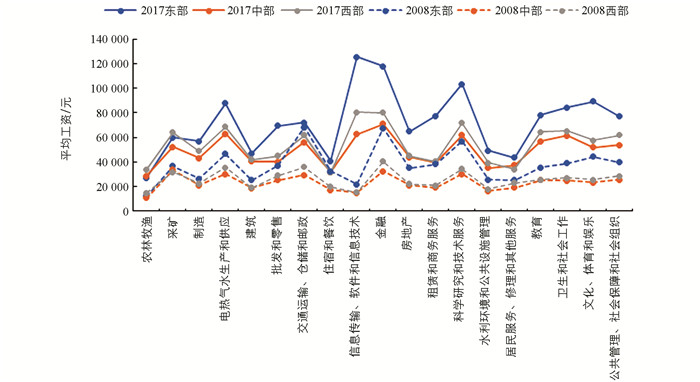
除就业机会之外,不同行业间的收入差距问题日益成为中国贫富差距问题的主要内容[2]. 图 1描绘了2008年与2017年的中国东、中、西部各行业收入水平,其中2017年的行业收入按照居民消费价格指数平减至2008年的水平. 由图 1可以看出,高技术附加值行业的收入通常高于低技术附加值行业,但不同地区的各行业收入变化呈现不同特征. 如在东部信息传输、软件与信息技术业,金融业,文化、体育和娱乐业,科学研究和技术服务业等高技术服务业的收入增加幅度明显高于其他区域,但是各区域农林牧渔业、建筑业等行业的收入变动幅度十分相近. 那么,高技术服务业发展下的就业扩张对其他行业的收入又产生了怎样的影响,在不同区域这一影响是否存在差异?
在讨论高技术附加值产业发展对其他行业劳动力的外部效应时,学者们主要从技能偏向型技术进步、产业结构高级化与人工智能发展等方面展开研究. 有学者认为,技能偏向型技术进步、产业结构高级化与人工智能发展会直接增加对高技能劳动力的需求,而当对高技能劳动力需求增加的速度快于教育发展的速度时[3],高技术产业的“创新驱动”发展会挤占其他产业的创新资源[4],还会进一步导致产业间劳动力收入差距的扩大. 但同时,高技术产业的发展也会通过知识溢出效应、乘数效应与消费创造效应,创造一定的低技术附加值就业岗位[4-6],生产技术、人工智能的发展一定程度也会增加其他行业劳动的生产能力[7]. 学者们在高技术产业发展对区域其他行业劳动力就业与工资的影响这一问题上并未得出一致结论[5, 8-10].
有关高技术服务业发展的研究更多集中于对其本身的发展效率[11]、与其他产业尤其是制造业的融合程度[12]以及高技术服务业和制造业协同集聚的经济效益[13]等方面,较少有学者直接研究高技术服务业发展的就业与收入外部性问题. 改善民生福祉是中国经济发展的主要目标,因此从劳动力市场角度出发,研究“创新驱动”下的高技术服务业就业扩张产生的外部性影响就十分必要.
国内学者在讨论技能偏向型技术进步、产业结构高级化与人工智能发展的就业市场效应时,也较少从行业收入差距视角切入,若从行业层面展开研究,又较少考虑中国经济发展存在的明显区域异质性[14]. 更重要的是,城市劳动力数量与技能结构的变化,也会影响劳动力在该城市所需的生活成本,而这进一步会对高技术产业就业扩张的外部性产生异质性影响,大多相关研究,在理论上也并未考虑这一因素[15]. 有学者[16]虽然在讨论人工智能对就业市场的结构重塑问题时,在劳动力需求端考虑了生活成本,但是在实际情况中,生活成本更多影响的是劳动力的效用函数,即劳动力供给端. 此外,现有从区域层面行业间收入差距视角开展的研究,多仅讨论至省际层面[17].
鉴于以上不足,本文从劳动力市场视角,开展高技术服务业就业扩张的外部性研究,可能的边际贡献在于:一是把握“创新驱动发展”主要体现在生产端的特征,同时考虑不同产业在创新发展过程中的特性与互动关系及中国区域间经济特征存在显著差异性的经济现实,从城市层面全面系统地分析高技术服务业发展对其他行业劳动力就业与工资影响. 二是在ENRICO[18]空间一般均衡模型的基础上,引入高技术服务业劳动力的技术外溢机制,考虑城市生活成本要素,推演求解高技术服务业就业增加后本地技能异质性劳动力的均衡数量与均衡工资,丰富与发展相关研究的理论成果. 三是相较于已有文献更多关注就业结构、工资溢价等相对变量,本文更为关注产业劳动力的绝对就业数量与绝对实际工资变化,这也更加符合中国尚处于“创新驱动发展”初步阶段的现实,只有能够切实促进所有劳动力在“创新驱动发展”背景下绝对福利水平的提升,谈相对社会福利的改善才更有意义.
全文HTML
-
本文在ENRICO[18]构建的空间一般均衡模型基础上,进一步引入行业异质性与高技术附加值行业对其他行业的技术外溢机制,从理论上分析区域高技术服务业就业增加对其他行业劳动力就业与实际工资的外部效应.
假设存在两期完全竞争市场经济,有a,b两个城市,每个城市存在高技术服务业厂商与其他行业厂商分别雇佣劳动力NHc与NLc,分别生产高技术附加值服务品YHc与其他商品YLc(c=a,b). 产品可在全国范围自由流通且不存在运输成本,因此同质商品的价格在a,b两市完全相同. 同时全国的劳动力总数N及高、低技能劳动力总数NH、NL均不会发生变化. 劳动者与厂商均可在城市间自由流动,并在效用最大化与利润最大化的条件下进行区位选择.
城市c高技术服务业劳动力的间接效用函数为:
其他行业劳动力的间接效用函数为:
其中,WHc与WLc分别为c市高技术服务业劳动力与其他行业劳动力的工资水平;Rc为住房消费价格,假定各行业劳动力面对同一住房市场;AHc与ALc为高技术服务业与其他行业劳动力对城市基础设施水平的评价;EHic与ELic是个体i对城市c的个人偏好.
假设劳动力对城市的个人偏好服从均匀分布:
SH、SL衡量了劳动力对城市个人偏好在其居住地选择中的重要性,同时也衡量了劳动力的流动弹性,S越大,说明劳动力对城市个人偏好在其居住地选择中更为重要,个体的流动弹性越小. 当边际劳动力在城市a与b间的效用无差异时,两城市的人口分布达到均衡.
所以,劳动力在城市a、b间的分布为:
式(4)与式(3)相减可得b市高技术服务业与其他行业劳动力市场的供给函数为:
由于本文讨论的是不同行业间劳动力的福利互动效应,产业间各要素在生产过程的互补性十分有限. 因此,本文假设生产要素间替代弹性为1,即不考虑要素间的互补性,进而假设城市c(c=a,b)厂商的生产函数为Cobb-Douglas形式且规模报酬不变,具体为:
其中,YHc与YLc为c市高技术服务业与其他行业的产出,XHc与XLc为相应技术水平,NHc与NHL为投入的劳动力总量,KHc与KLc为投入的资本总量. 假设高技术附加值服务品价格为Ph,其余行业生产商品价格为1,资本无限供给且价格为I. 从而在利润最大化的一阶条件下,可得劳动力与资本的需求函数分别为:
最后为简化分析,假设城市住房的供给与所属权与本地人无关,具体住房供给函数设定为:
Z为初始生活成本,假设各城市该值相同. Qc衡量了c城市的生活成本对人口规模的敏感程度,刻画了住房供给弹性. 当城市住房供给弹性越小,Qc取值越大,人口增加将更大程度地引起房价上涨.
至此,本文构建的理论模型在同时实现劳动力、资本与住房三个市场供求均衡时便可得到空间一般均衡解.
现假设,b城市高技术服务行业在第2期发生技术进步,其技术水平提升ΔH,即:
由式(3)(8)(9)(10)可知,b市高技术服务业这一技术水平上的外生冲击将会通过影响其劳动力需求进而改变该行业劳动力在城市间的分布. 而若一城市高技术服务行业的劳动力数量增加,往往会推动本地其他行业劳动力生产力的提高. 这一方面是由于在技术进步推动下的高技术服务业就业扩张会增加对高技能劳动力的需求,而高技能劳动力会在产业合作、社区生活等活动中对其他行业劳动力产生知识外溢;另一方面则是因为高技能劳动力的增加会产生更多的家政、外卖等服务需求,进而刺激其他行业劳动力的需求增加,并寻求更为高效的生产方式. 因而有:
由式(8)(9)(10)可得:
进一步代入式(3)有:
由式(16)可知,当高技术服务业劳动力对其他行业劳动力的生产力外溢作用越强,即λ′取值越大,城市的住房供给弹性越大,即Qa与Qb的取值越小,城市高技术服务业劳动力的数量增加将更大程度地促进其他行业劳动力在本地的集聚. 而低技能劳动力对地域的个体偏好性越强,即SL取值越大,则会越大程度地削弱这一集聚效应.
联立式(16)与(17)可得:
由式(18)可知,当高技术服务业出现一个正向的技术冲击时,将使得区域高技能劳动力数增加. 现联立式(3)(15)(16)与(18)以分析城市高技术服务业劳动力数量对本地其他行业劳动力实际工资的影响,可得:
式(19)(20)说明,城市高技术服务业就业扩张对其他行业劳动力实际工资的影响取决于劳动力生产力正向外溢作用的大小与该城市的住房供给弹性:越显著的知识外溢作用(λ′取值越大),与更宽松的住房供给市场(Qb)取值越小,本地高技术服务业就业扩张将越有可能促进其他行业劳动力实际工资的提升. 式(16)与(19)(20)对比分析可知,倘若高技术服务业就业扩张促进了其他行业的就业,那么也必然对其他行业劳动力的实际工资水平产生正向影响.
基于以上理论分析可知,城市大力推动创新发展和技术进步,将推动高技术服务业的就业扩张. 而这种就业扩张对于其他行业劳动力就业数与实际工资的影响,则取决于高技能劳动力的技术外溢强度与本地生活成本的波动大小,主要体现为住房价格的涨幅. 随着技术外溢强度的增加与住房供给弹性的提升,高技术服务业对其他行业劳动力就业与实际工资的促进作用将更为显著. 而若技术外溢作用有限,城市住房供给弹性甚低,高技术服务业的就业扩张会对其他行业劳动力就业产生负向挤出并使其实际工资下降. 在我国,城市高技术服务业的劳动力增加对其他行业劳动力就业和实际工资的影响究竟如何,本文将进一步使用经验数据,分别构建实证模型加以分析.
-
上式为本文计量模型1的设定,主要参考了ENRICO [5]、LEE等[10]的研究构建了就业乘数模型. 其中,被解释变量Δlnnonhsc表示城市c于2008-2017年非高技术服务业的从业人员数对数的变化值,核心解释变量Δlnhservicec为2008-2017年c城市高技术服务业从业人员数对数的变化值,Xc为一系列城市层面的控制变量,εc为扰动项. 之所以选择这段时期,是基于“创新驱动发展”战略于2012年党的十八大正式提出,2008至2017十年能够在时间上较为对称的考量,创新驱动下高技术服务业发展对于其他行业劳动力就业的影响. α、γ均是参数,β1是重点关注的系数.
该模型可能存在遗漏变量的内生性问题,本文参考LEE等[10]的做法,使用改进后的份额转移(shift-share)[19]工具变量. 具体形式如式(22)所示. 其中,
$E_{c, t}^j$ 为c市t时j行业就业数(j∈hservice),$E_{c, t}^{hservice }$ 为c市t时高技术服务业就业数,$E_{all, t}^{hservice }$ 为全国t时高技术服务业就业数,$\Delta {{\overset\frown{lnhservice}}_{c}}$ 为c市2008-2017年高技术服务业就业数对数变化的shift-share工具变量. 该工具变量对于2008-2017年各城市高技术服务业就业增长量的预测是基于全国除该市外,其他城市在2008-2017年的高技术服务业就业增长率之上的,并以本地期初各行业发展情况为权重,这样可以很好地排除当年本地城市层面未观测到的干扰项的影响.进一步地,本文构建面板数据模型以分析高技术服务业劳动力数量对本地其他行业劳动力实际工资的影响. 考虑到技术外溢的正向作用与生活成本上涨的负向作用使城市高技术服务业劳动力数量变化与其他行业劳动力的工资变化之间可能存在非线性关系,因此在模型中增加高技术服务业劳动力数的二次项. 计量模型2具体形式如下:
lnnswagec,t为城市c非高技术服务业劳动力在t(t∈[2014, 2017])时平均工资的对数. 本文在以上模型中均采用去除物价影响的实际变量. lnhservicec,t为c市t时高技术服务业从业数对数. Xc,t为一系列随时间变动的,可能影响非高技术服务业从业人员工资水平的城市层面控制变量. 此外,φc控制了不随时间变动的城市固定效应,δt则控制了时间固定效应,εc,t为随机扰动项,β1、β2为该模型分析重点关注系数.
模型2也可能存在遗漏变量等内生性问题,因此本文同样采用基于其他地区增长率预测的该地高技术服务业就业人数作为shift-share工具变量,具体形式参考KEMENY等[9]的做法,如公式(24)所示.
-
为分析城市高技术服务业的就业扩张对本地其他行业劳动力就业机会与工资待遇的影响,在模型1的实证分析中,本文使用了各城市在研究期间内高技术服务业从业人员数对数的变化值(Δlnhservice)为核心解释变量,在模型2则使用了各年各城市的高技术服务业从业人员数对数(lnhservice)作为核心解释变量. 而关于高技术服务业的定义,由于城市层面的分行业就业数据只明确到行业大类代码即19大类,本文在4位行业代码基础上,将国家统计局颁布的《高技术产业(服务业)分类(2018)》与《国民经济行业分类》(GB/T 4754-2017)相对应,将《高技术产业(服务业)分类(2018)》中在4位代码水平上涉及的行业界定为“高技术服务业”. 匹配后,本文定义的高技术服务业主要包括:信息传输、软件和信息技术业,金融业,租赁和商务服务业,科学研究和技术服务业,水利环境和公共设施管理业及文化、体育和娱乐业. 该变量相关数据来源于2009-2018年《中国城市统计年鉴》.
关于被解释变量,本文在实证模型1中使用了各城市的非高技术服务业就业数对数变化值(Δlnnonhs),在模型2中则为各城市的非高技术服务业从业人员平均工资对数(lnnswage). 其中,非高技术服务业指19类行业中的除去高技术服务业的行业,具体包括农林牧渔业,采矿业,制造业,电热气水生产和供应业,建筑业,批发和零售业,交通运输、仓储和邮政业,住宿和餐饮业,房地产业,居民服务、修理和其他服务业,教育业,卫生和社会工作业,公共管理、社会保障和社会组织业. 各城市的非高技术服务业就业数据来源于2009-2018年城市统计年鉴.
而对于模型2中被解释变量lnnswagec,t的衡量,由于《中国城市统计年鉴》并未公布相关数据,而大多微观调查数据或对个体样本所属城市进行了加密处理,或其行业划分与国家统计局所明晰的国民经济行业分类标准并不一致,无法适用于本文研究. 本文选择全国流动人口动态监测调查(CMDS)数据整理得到各年各城市非高技术服务业流动人口的平均工资,对lnnswagec,t变量加以衡量. 由于2014年前CMDS问卷中有关流动人口从事行业的分类方法与2014年后存在差异,并且无法与《国民经济行业分类》(GB/T 4754-2017)进行精确匹配,最后使用了2014-2017年的CMDS数据开展模型2的实证研究.
流动人口动态监测调查以当年所有流动人口为抽样总体,采取PPS抽样方法,每个样本点抽样调查人员20至30人. 本文在数据处理过程中剔除了当年非高技术服务业观测样本少于50的城市,即最终选择的样本城市在抽样调查中至少包括3个抽样样本点,以保证统计所得各城市低技术产业劳动力平均工资具有一定代表性. 同时,在稳健性检验中,本文进一步提高进入研究样本的标准,将50人提升至100人,并在计算各城市低技术产业劳动力平均工资时进行双侧1%缩尾. 未在基准回归中采用基于这一更为严格要求所保留的城市样本,主要是基于对样本容量与样本选择偏误问题的考虑. 当然另一不可忽视的问题是,流动人口相较于本地人往往面临更为严峻的就业市场环境,根据其计算得到的各城市非高技术服务业劳动力平均工资可能会略低于全样本下的统计结果. 因而,倘若本文估计认为高技术服务业的就业扩张损害了其他行业劳动力的工资福利,这一变量度量上的问题将直接影响本文结论的可信度,而若估计结果为促进作用抑或正、倒U形影响,这一度量方法只会使得促进作用被低估,拐点位置被右或左移,并不会对关系的方向产生实质性影响.
控制变量选择方面,在就业效应模型中,本文主要控制了会影响城市非高技术服务业就业人数或同时影响高技术服务业与其他行业就业人数的干扰性因素. 一方面,参考LEE等[10]的做法,主要控制了城市聚集效应—人口密度(lnpeople,等于城市户籍人口数除以其行政面积对数)、整体就业水平—期末从业人员数对数(lnworker)、人力资本状况—每千人普通高校在校学生数对数的影响(lnstudent). 另一方面,加入影响中国城市人口流动的主要因素,具体有公共服务完善度—每千人医院卫生院床位数(hospital)、空气质量—每十亿元GDP工业二氧化硫排放量(SO2)、生活成本—住宅平均销售价格(rent)、经济潜力—是否为港口城市(port)等指标,分别控制了城市在研究期间初始的公共服务水平、空气质量状况、房价水平以及地理位置条件. 所有控制变量取2008年值.
对于工资效应模型中的控制变量,考虑影响区域工资水平与非高技术服务业劳动力工资水平的因素. 参考VAN DIJK[8]和BARTIK[19]的做法,本文主要选取以下指标:就业密度—城镇单位非农产业就业人数与全市行政区域土地面积之比的对数(lndensity),人力资本水平—每千人普通高校在校生人数对数(lnstudent),平均工资水平—在岗职工月平均实际工资(wage),产业结构高级化程度—第三产业产值占GDP比重(industry).
在对模型1与模型2解释变量进行多重共线性检验后,对模型1中的在岗职工工资与住宅平均销售价格取比值处理. 本文对大多控制变量取对数处理. 控制变量数据主要来自CEIC中国经济数据库、2009-2018年《中国城市统计年鉴》及各市统计年鉴.
-
表 1展示了在本文实证分析中主要使用变量的描述性特征. 首先对模型1与模型2的观测样本数予以说明,在模型1中的观测样本为研究期间内中国26个省(自治区)的地级市和4个直辖市(未含港、澳、台、西藏),而模型2由于部分城市存在数据缺失,在模型1研究样本的基础上构建了211个地级市的平衡面板展开分析. 其中由于部分城市的普通高校在校学生数为0或数据缺失,因而lnstudent变量的观测值小于其他变量.
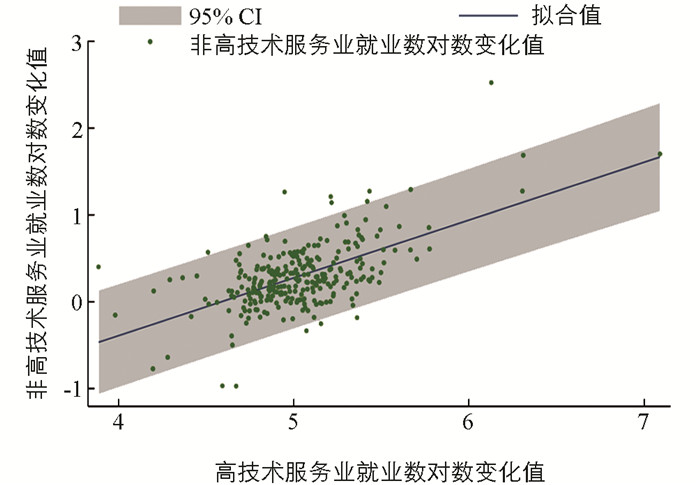
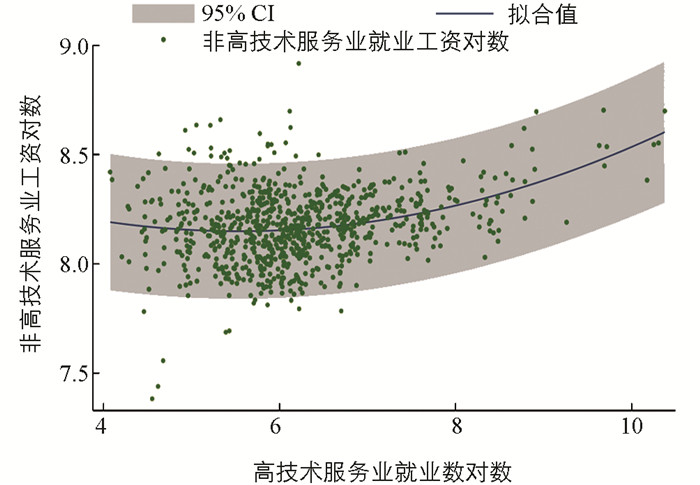
可以发现在模型1的研究期间内,高技术服务行业的就业增加量明显高于非高技术服务行业,且对于所有城市样本,在研究期间内高技术服务业的就业人数均有显著增加,而对于非高技术服务行业,存在部分城市在研究期间内其就业量有所下降的情况. 同时,非高技术服务行业的就业变化相较于高技术行业,存在更为明显的地区间差异. 对于模型2,则发现相较于地区的平均工资水平,非高技术服务业劳动者的工资无论是最大值、最小值抑或平均值都处于更低的水平. 而对于高技术服务业就业数与非高技术服务业劳动力的工资收入间关系较难直接通过表 1体现. 因此本文基于研究数据分别绘制了高技术服务业就业数对数的变化值与同时期各地区非高技术服务行业就业数对数变化值、高技术服务业就业数对数与非高技术服务业劳动力工资对数间的相关性关系图.
由图 2可知,2008-2017年间,中国城市高技术服务业与其他行业从业人员数均存在明显增长,同时可初步判断,两者存在正向相关关系. 图 3则表明了城市间非高技术服务业从业人员工资水平同样存在明显差异,而非高技术服务业劳动力实际工资水平与高技术服务业从业数两者间大致呈正U形关系.
2.1. 研究模型
2.2. 主要变量定义及数据来源
2.3. 关键变量描述性分析
-
表 2报告的是模型1的基本回归结果. 前3列分别为全样本未加入控制变量、加入控制变量,以及使用shift-share工具变量的回归结果,其中,2SLS(两阶段最小二乘法)的一阶段回归F值为24.092 1,拒绝弱工具变量假设. 对于各列估计样本量的细微差别有必要说明. 一方面,由于部分控制变量存在数据缺失问题,因而第(2)(3)列与第(5)(6)列分别较第(1)(4)列样本观测数有所减少;另一方面,表 2(4)(5)(6)列为剔除通过杠杆统计量判断所得的离群城市样本(东莞市与兰州市)后的相应估计结果. 表 2的估计结果显然说明,城市高技术服务业就业数增加对地区其他行业就业数始终为显著的正向促进作用. 从第(3)列估计结果可以看出,在中国,平均某城市高技术服务业就业增加1%将带来其他行业就业大约0.58%的增加. 参考ENRICO[5]、LEE等[10]的研究将该弹性与研究基期中国非高技术服务业从业人员数和高技术服务业从业人员数的比值相乘,由2009年《中国城市统计年鉴》相关统计数据可得,2008年中国非高技术服务业从业人员数与高技术服务业从业人员数的比值为7.44,将其与弹性0.58相乘即可计算出:平均而言,中国城市高技术服务业每增加一个就业,会促使本地其他行业增加大约4.32个就业.
表 3为模型2的基准回归结果,前两列为未考虑内生性问题时的OLS回归结果,最后一列为使用shift-share工具变量,运用2SLS法的回归结果,同样地,由于第(2)(3)列在回归中加入了控制变量,因而较第(1)列样本量有所减少. 可以发现表 3各列中,城市高技术服务业就业数一次项前的系数始终显著为负,二次项前的系数则始终显著为正. 说明中国高技术服务业从业人员数与其他行业从业人员平均工资呈显著正U形关系. 为避免将实际为单调凸形的关系误判为U形关系,本文进一步对模型2进行U形检验. 结果显示,U形关系实际存在,拐点位置大致在6.42,即平均意义上,当城市高技术服务业从业人员数高于大约614万后(6.42取指数函数可得,当然如前文所述,由于使用数据局限,实际情况这一拐点可能会更早到来),就业创造效应才能超越城市生活成本上涨效应,对其他行业从业人员的平均实际工资产生正向促进作用.
-
为确保研究结果的可靠性,本文对回归1与回归2分别开展以下稳健性检验.
对于回归1,一方面由于高技术服务业在全国范围内的布局呈现一定区域集聚性. 本文进一步从城市样本中剔除直辖市、省会城市及深圳市进行2SLS回归. 另一方面,在基础回归所界定的“高技术服务业”中,有部分隶属于金融业,租赁和商务服务业,水利环境和公共设施管理业以及文化、体育和娱乐业的4位行业,其并非都属于《高技术产业(服务业)分类(2018)》文件中所界定的“高技术产业(服务业)”,本文进一步将高技术服务业的涵盖范围缩小,主要包括信息传输、软件和信息技术业,科学研究和技术服务业,开展2SLS回归分析. 以上回归结果分别如表 4第(1)(2)列所示,发现高技术服务业就业扩张对其他行业的就业增加外部效应依然显著.
在模型2的设定下,本文开展了更为丰富的稳健性检验:第一,采取滞后一期控制变量的模型设定,对研究问题重新检验,检验结果如表 5第(1)列所示. 第二,同样从城市样本中剔除直辖市、省会城市及深圳市进行2SLS回归,回归结果由表 5第(2)列所示. 第三,由于本文各城市非高技术服务业劳动力的平均工资数据是基于流动人口动态监测调查微观数据加总后求算术平均值而得,因此证明该数据的地区代表性尤为重要. 本文在此针对各个城市非高技术服务业劳动力平均工资,设定更为严格的计算方法,即对微观数据进行双侧1%缩尾,并将观测值小于100、涉及观测点小于5个的城市样本剔除,结果见表 5第(3)列. 第四,将“高技术服务业”界定为包括信息传输、软件和信息技术业,科学研究和技术服务业. 调整定义后的2SLS回归结果如表 5第(4)列所示,与基础回归一致. 第五,考虑城市的平均工资水平可能在时间上具有相关性,本文以理论、sargen检验和序列相关检验的结果为依据,选择最优的模型设定对研究问题进行GMM(Generalized method of moments)的再估计,其中,由于GMM估计需要使用前期的观测值构造工具变量,因而样本量出现较为明显的下降. GMM估计的结果如表 5第(5)列所示,基础回归结果依然稳健.
3.1. 基准回归结果分析
3.2. 稳健性检验
-
由前面理论分析可知,地区的现有房地产市场环境、产业结构下的知识溢出强度等会对本文研究问题产生显著影响. 因此,本文以各城市间的住房供给弹性与产业结构合理化水平的差异为基础,进行地区层面的异质性分析. 若这一异质性显著,可进一步排除对本文基础回归结果的相关竞争性解释. 并且,本文进一步将高技术服务业细分为“高精尖”的高技术服务业与其他高技术服务业,从产业角度开展相关异质性分析,试图发掘中国城市在“创新驱动”背景下的产业发展可能存在的更多问题.
-
本文以2013年中国各城市的住房供给弹性为依据,将高于或低于平均水平的城市分别划分为高住房供给弹性城市(h-elasticity)与低住房供给弹性城市(l-elasticity). 之所以选取2013年,一方面是受数据限制,本文仅能获得2013年各城市住房供给弹性的数据,另一方面是因为2013年处于就业效应差分方程分析的中间时段,同时也是工资效应面板模型分析的期初时点,以该年数据作为划分依据,具有理论意义. 而各城市住房供给弹性数据源于刘修岩等[20]的研究. 表 6(1)(2)列展示了相关2SLS分组回归结果. 研究发现,高住房供给弹性城市的高技术服务业就业增加能够显著促进其他行业就业的增加,但低住房供给弹性这一关系并不显著. 这验证了本文理论的分析,当城市住房供给弹性较小,高技术服务业从业者在区域的集聚会导致房价更高幅度的上涨,而增幅明显的生活成本会抑制其他行业劳动力在城市的定居. 在高住房供给弹性的城市,高技术服务业就业增加对其他行业劳动力工资的影响并不显著,但在低住房供给弹性地区,两者间的U形关系十分显著. 结合描述性统计特征可知,目前我国城市大多仍处于拐点左侧,即在低住房供给弹性地区,高技术服务行业发展对其他行业从业人员工资的负向影响更为显著.
-
根据本文论述,高技术服务业与其他行业间的合作既是知识外溢的重要途径,也是推动地区增加对其他行业劳动力需求的重要诱因. 因此,本文参考韩永辉等[21]对产业结构合理度的测量方式,以2013年各城市的产业结构合理化水平为依据,将城市划分为产业结构高合理化(h-RIS)与产业结构低合理化(l-RIS)两类,并分组进行就业效应与工资效应的实证研究. 结果如表 6(3)(4)列所示,无论是产业结构合理化高的城市还是较低的城市,高技术服务业的就业扩张均显著促进了其他行业的就业增长,且在产业结构合理化程度更高的地区,高技术服务业的就业正外部效应更为显著. 考虑工资效应则可以发现,在产业结构合理化程度更高的城市,高技术服务业就业扩张能产生显著更为平缓的边际工资效应,拐点也将显著右移. 即当城市产业结构较为合理时,高技术服务业发展下高技能劳动力在区域的集聚能够在一开始就对其他行业劳动力产生知识外溢,提高其生产力,并使非高技术服务业新增对劳动力的需求,使其实际工资更高幅度地提升. 即使在拐点之后,高技术服务业的就业增加,依然有利于其他行业劳动力的实际工资上涨,虽然增速较为平缓. 这可能是中国产业结构合理化水平较高的城市,高技术服务业的技术附加值有限,未能产生更大幅度的正向工资效应. 但就基础回归结果可知,目前中国大多城市仍处于工资效应的拐点左侧,因此,在发展高技术服务业的同时,注重与其他产业的结构优化尤为必要.
-
为进一步探究区域异质性分析结果的可能原因,本文依据2014-2018年《中国劳动统计年鉴》中的全国各行业受教育程度构成数据,将大学本科及研究生占比最高的3个行业,即科学研究和技术服务业,金融业,信息传输、软件和信息技术业,划分为“高精尖”的高技术服务业(tech-hservice). 实证结果如表 7、表 8所示.
研究发现,目前中国“高精尖”的高技术服务业对其他行业劳动力的就业促进效应并不显著,但会对其他行业劳动力的实际工资产生正U形影响. 而相对劳动力技能水平更低的高技术服务业,其就业人数增加对其他行业劳动力具有正向的就业效应和负向的实际工资效应. 这可能是由于,中国“高精尖”高技术服务业占比高的城市多为户籍限制相对严格、住房供给弹性相对较低的地区. 而非“高精尖”的高技术服务业就业增加,对其他行业劳动力的实际工资水平目前更多的是不利影响. 一方面是因为其技术附加值有限,对非高技术服务业劳动力产生的生产力方面的知识溢出效应有限;另一方面是由于大量发展非“高精尖”高技术服务业的地区,多为技术、科研基础较为薄弱地区,在推动创新发展战略,引进高技术服务业入驻本地时,忽略了其与本地现有产业结构的适应性,从而产生的知识外溢作用有限[22].
4.1. 住房供给弹性与外部效应
4.2. 产业结构合理度与外部效应
4.3. 不同技术附加值外部效应
-
本文在理论上构建考虑了高技术服务业与其他行业劳动力之间技术外溢机制与城市住房供给弹性差异的空间一般均衡模型,并在实证上利用中国城市中观数据与流动人口动态监测调查微观数据,研究了创新驱动发展背景下,中国城市高技术服务业就业增加对本地其他行业劳动力就业与工资的影响. 研究结论如下:
(1) 使用就业乘数模型估计得到:中国城市非高技术服务业就业数对高技术服务业从业人员数的弹性为0.58,高技术服务业的就业乘数约为4.32.
(2) 使用双向固定效应模型发现:中国城市高技术服务业就业数与其他行业劳动力工资水平呈正U形关系,平均而言,拐点大致为城市高技术服务业从业人员数达到614万后.
(3) 异质性分析表明:城市住房供给市场有足够弹性是保证高技术服务业就业促进作用发挥的重要条件. 在高技术服务业发展初期,城市产业结构合理化程度的提高,能够减少高技术服务业就业增加对其他行业劳动力实际工资的负向影响. 而在城市高技术服务业发展较为成熟后,提高其技术附加值尤为重要.
此外,要发挥“高精尖”的高技术服务业的积极就业效应,就需要降低当地要素流动壁垒与城市住房供给弹性. 而若高技术服务业存在技术附加值低和地区产业配套程度低等问题,可能会对非高技术服务业的劳动力实际工资产生显著负向影响.
综合上述研究结论,本文得到以下政策启示:(1) 各地应坚持贯彻落实创新驱动发展战略,不断提高本地产业的技术附加值,推动高技术服务业在区域的发展,并最大程度地帮助高技术服务业就业扩张在劳动力市场的积极外部效应发挥. (2) 应通过增加高技术服务业与其他行业间劳动力的生产技能知识交流,增加住房建设用地供给以提高住房供给弹性,出台扶持、补贴政策等方式,帮助其他行业技能或工资水平更低的劳动力留下来,成功在城市实现就业. (3) 应当有差别地落实创新驱动发展战略. 创新基础较为薄弱的地区,应更为重视“因地制宜”地发展高技术服务业,注意新引进高技术服务业与地区现有产业结构的协调性,不断在产业结构高级化中保障与提升地区产业结构的合理度,进而为产业间的知识外溢效应发挥提供有利土壤. 而创新基础较好地区要致力于不断提高本地高技术服务业的附加值,发展“高精尖”的高技术服务业,推动高技术服务就业扩张,实现劳动力市场外部效益的最大化与可持续发展.
最后,由于数据限制,本文经研究对地区高技术服务业劳动力增加的就业效应方向与大小以及工资效应的方向虽然得到较为准确的结论,但是可能存在对高技术服务业就业扩张的工资积极外部性低估的问题. 这也是未来有待进一步研究的方向.



 下载:
下载: